Exact Factorization Adventures: A Promising Approach for Non-Bound States
Abstract
:1. Introduction
2. The XF Approach in a Nutshell
2.1. XF Adventures in Different Realms
3. Exact Potentials Driving Dissociation and Ionization
4. XF-Based Mixed Quantum-Classical Methods
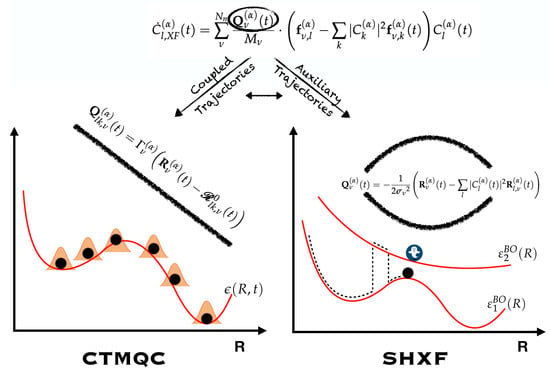
4.1. Computation of the Quantum Momentum
5. Computing the Quantum Momentum
5.1. ECR Model a.u.
5.2. ECR Model a.u.
6. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crespo-Otero, R.; Barbatti, M. Recent Advances and Perspectives on Nonadiabatic Mixed Quantum–Classical Dynamics. Chem. Rev. 2018, 118, 7026–7068. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agostini, F.; Curchod, B.F.E. Different flavors of nonadiabatic molecular dynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2019, 9, e1417. [Google Scholar] [CrossRef]
- Thachuk, M.; Ivanov, M.Y.; Wardlaw, D.M. A semiclassical approach to intense-field above-threshold dissociation in the long wavelength limit. J. Chem. Phys. 1996, 105, 4094–4104. [Google Scholar] [CrossRef]
- Thachuk, M.; Ivanov, M.Y.; Wardlaw, D.M. A semiclassical approach to intense-field above-threshold dissociation in the long wavelength limit. II. Conservation principles and coherence in surface hopping. J. Chem. Phys. 1998, 109, 5747–5760. [Google Scholar] [CrossRef]
- Bajo, J.J.; González-Vázquez, J.; Sola, I.; Santamaria, J.; Richer, M.; Marquetand, P.; González, L. Mixed quantum-classical dynamics in the adiabatic representation to simulate molecules driven by strong laser pulses. J. Phys. Chem. A 2012, 116, 2800. [Google Scholar] [CrossRef]
- Horenko, I.; Schmidt, B.; Schütte, C. A theoretical model for molecules interacting with intense laser pulses: The Floquet-based quantum-classical Liouville equation. J. Chem. Phys. 2001, 115, 5733–5743. [Google Scholar] [CrossRef] [Green Version]
- Fiedlschuster, T.; Handt, J.; Schmidt, R. Floquet surface hopping: Laser-driven dissociation and ionization dynamics of H2+. Phys. Rev. A 2016, 93, 053409. [Google Scholar] [CrossRef]
- Schirò, M.; Eich, F.G.; Agostini, F. Quantum-classical nonadiabatic dynamics of Floquet driven systems. J. Chem. Phys. 2021, 154, 114101. [Google Scholar] [CrossRef]
- Lépine, F.; Ivanov, M.Y.; Vrakking, M.J.J. Attosecond molecular dynamics: Fact or fiction? Nat. Photonics 2014, 8, 195. [Google Scholar] [CrossRef]
- Hunter, G. Conditional probability amplitudes in wave mechanics. Int. J. Quantum Chem. 1975, 9, 237. [Google Scholar] [CrossRef]
- Hunter, G. Ionization potentials and conditional amplitudes. Int. J. Quantum Chem. 1975, 9, 311. [Google Scholar] [CrossRef]
- Hunter, G. Nodeless wave function quantum theory. Int. J. Quantum Chem. 1980, 9, 133. [Google Scholar] [CrossRef]
- Hunter, G. Nodeless wave functions and spiky potentials. Int. J. Quantum Chem. 1981, 19, 755. [Google Scholar] [CrossRef]
- Hunter, G.; Tai, C.C. Variational marginal amplitudes. Int. J. Quantum Chem. 1982, 21, 1041. [Google Scholar] [CrossRef]
- Gidopoulos, N.I.; Gross, E.K.U. Electronic non-adiabatic states: Towards a density functional theory beyond the Born–Oppenheimer approximation. Philos. Trans. R. Soc. Lond. A: Math. Phys. Eng. Sci. 2014, 372, 20130059. [Google Scholar] [CrossRef] [Green Version]
- Abedi, A.; Maitra, N.T.; Gross, E.K.U. Exact Factorization of the Time-Dependent Electron-Nuclear Wave Function. Phys. Rev. Lett. 2010, 105, 123002. [Google Scholar] [CrossRef] [Green Version]
- Abedi, A.; Maitra, N.T.; Gross, E.K.U. Correlated electron-nuclear dynamics: Exact factorization of the molecular wavefunction. J. Chem. Phys. 2012, 137, 22A530. [Google Scholar] [CrossRef] [Green Version]
- Agostini, F.; Gross, E.K.U. Ultrafast dynamics with the exact factorization. Eur. Phys. J. B 2021, 94, 179. [Google Scholar] [CrossRef]
- Suzuki, Y.; Abedi, A.; Maitra, N.T.; Yamashita, K.; Gross, E.K.U. Electronic Schrödinger equation with nonclassical nuclei. Phys. Rev. A 2014, 89, 040501(R). [Google Scholar] [CrossRef]
- Khosravi, E.; Abedi, A.; Maitra, N.T. Exact Potential Driving the Electron Dynamics in Enhanced Ionization of H2+. Phys. Rev. Lett. 2015, 115, 263002. [Google Scholar] [CrossRef] [Green Version]
- Ha, J.K.; Lee, I.S.; Min, S.K. Surface Hopping Dynamics beyond Nonadiabatic Couplings for Quantum Coherence. J. Phys. Chem. Lett. 2018, 9, 1097–1104. [Google Scholar] [CrossRef]
- Lee, I.S.; Ha, J.K.; Han, D.; Kim, T.I.; Moon, S.W.; Min, S.K. PyUNIxMD: A Python-based excited state molecular dynamics package. J. Comput. Chem. 2021, 42, 1755–1766. [Google Scholar] [CrossRef] [PubMed]
- Pieroni, C.; Agostini, F. Nonadiabatic Dynamics with Coupled Trajectories. J. Chem. Theory Comput. 2021, 17, 5969–5991. [Google Scholar] [CrossRef] [PubMed]
- Min, S.K.; Agostini, F.; Gross, E.K.U. Coupled-Trajectory Quantum-Classical Approach to Electronic Decoherence in Nonadiabatic Processes. Phys. Rev. Lett. 2015, 115, 073001. [Google Scholar] [CrossRef] [PubMed]
- Agostini, F.; Min, S.K.; Abedi, A.; Gross, E.K.U. Quantum-Classical Nonadiabatic Dynamics: Coupled- vs Independent-Trajectory Methods. J. Chem. Theory Comput. 2016, 12, 2127–2143. [Google Scholar] [CrossRef] [Green Version]
- Min, S.K.; Agostini, F.; Tavernelli, I.; Gross, E.K.U. Ab Initio Nonadiabatic Dynamics with Coupled Trajectories: A Rigorous Approach to Quantum (De)Coherence. J. Phys. Chem. Lett. 2017, 8, 3048–3055. [Google Scholar] [CrossRef]
- Khosravi, E.; Abedi, A.; Rubio, A.; Maitra, N.T. Electronic non-adiabatic dynamics in enhanced ionization of isotopologues of hydrogen molecular ions from the exact factorization perspective. Phys. Chem. Chem. Phys. 2017, 19, 8269–8281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abedi, A.; Maitra, N.T.; Gross, E.K.U. Response to “Comment on ‘Correlated electron-nuclear dynamics: Exact factorization of the molecular wavefunction’” [J. Chem. Phys. 139, 087101 (2013)]. J. Chem. Phys. 2013, 139, 087102. [Google Scholar] [CrossRef] [Green Version]
- Fiedlschuster, T.; Handt, J.; Gross, E.K.U.; Schmidt, R. Surface hopping in laser-driven molecular dynamics. Phys. Rev. A 2017, 95, 063424. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, Y.; Abedi, A.; Maitra, N.T.; Gross, E.K.U. Laser-induced electron localization in H2+: Mixed quantum-classical dynamics based on the exact time-dependent potential energy surface. Phys. Chem. Chem. Phys. 2015, 17, 29271–29280. [Google Scholar] [CrossRef] [Green Version]
- Abedi, A.; Agostini, F.; Suzuki, Y.; Gross, E.K.U. Dynamical steps that bridge piecewise adiabatic shapes in the exact time-dependent potential energy surface. Phys. Rev. Lett. 2013, 110, 263001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agostini, F.; Abedi, A.; Suzuki, Y.; Gross, E.K.U. Mixed quantum-classical dynamics on the exact time-dependent potential energy surfaces: A novel perspective on non-adiabatic processes. Mol. Phys. 2013, 111, 3625. [Google Scholar] [CrossRef] [Green Version]
- Agostini, F.; Abedi, A.; Suzuki, Y.; Min, S.K.; Maitra, N.T.; Gross, E.K.U. The exact forces on classical nuclei in non-adiabatic charge transfer. J. Chem. Phys. 2015, 142, 084303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Curchod, B.F.E.; Agostini, F. On the Dynamics through a Conical Intersection. J. Phys. Chem. Lett. 2017, 8, 831–837. [Google Scholar] [CrossRef] [Green Version]
- Curchod, B.F.E.; Agostini, F.; Gross, E.K.U. An exact factorization perspective on quantum interferences in nonadiabatic dynamics. J. Chem. Phys. 2016, 145, 034103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agostini, F.; Abedi, A.; Gross, E.K.U. Classical nuclear motion coupled to electronic non-adiabatic transitions. J. Chem. Phys. 2014, 141, 214101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abedi, A.; Agostini, F.; Gross, E.K.U. Mixed quantum-classical dynamics from the exact decomposition of electron-nuclear motion. Europhys. Lett. 2014, 106, 33001. [Google Scholar] [CrossRef] [Green Version]
- Davis, M.J.; Heller, E.J. Quantum dynamical tunneling in bound states. J. Chem. Phys. 1981, 75, 246. [Google Scholar] [CrossRef]
- Hughes, K.H.; Parry, S.M.; Parlant, G.; Burghardt, I. A hybrid hydrodynamic-liouvillian approach to mixed quantum-classical dynamics: Application to tunneling in a double well. J. Phys. Chem. A 2007, 111, 10269–10283. [Google Scholar] [CrossRef]
- Basire, M.; Borgis, D.; Vuilleumier, R. Computing Wigner distributions and time correlation functions using the quantum thermal bath method: Application to proton transfer spectroscopy. Phys. Chem. Chem. Phys. 2013, 15, 12591–12601. [Google Scholar] [CrossRef]
- Litman, Y.; Behler, J.; Rossi, M. Temperature dependence of the vibrational spectrum of porphycene: A qualitative failure of classical-nuclei molecular dynamics. Faraday Discuss. 2020, 221, 526–546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lawrence, J.E.; Manolopoulos, D.E. Path integral methods for reaction rates in complex systems. Faraday Discuss. 2020, 221, 9–29. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Giannini, S.; Lively, K.; Blumberger, J. Nonadiabatic dynamics with quantum nuclei: Simulating charge transfer with ring polymer surface hopping. Faraday Discuss. 2020, 221, 501–525. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Franco, I. Partial hydrodynamic representation of quantum molecular dynamics. J. Chem. Phys. 2017, 146, 194104. [Google Scholar] [CrossRef] [Green Version]
- Shushkov, P.; Li, R.; Tully, J.C. Ring polymer molecular dynamics with surface hopping. J. Chem. Phys. 2012, 137, 22A549. [Google Scholar] [CrossRef]
- Dupuy, L.; Lauvergnat, D.; Scribano, Y. Smolyak representations with absorbing boundary conditions for reaction path Hamiltonian model of reactive scattering. Chem. Phys. Lett. 2022, 787, 139241. [Google Scholar] [CrossRef]
- Suzuki, Y.; Watanabe, K. Bohmian mechanics in the exact factorization of electron-nuclear wave functions. Phys. Rev. A 2016, 94, 032517. [Google Scholar] [CrossRef] [Green Version]
- Talotta, F.; Agostini, F.; Ciccotti, G. Quantum trajectories for the dynamics in the exact factorization framework: A proof-of-principle test. J. Phys. Chem. A 2020, 124, 6764–6777. [Google Scholar] [CrossRef]
- Agostini, F.; Tavernelli, I.; Ciccotti, G. Nuclear Quantum Effects in Electronic (Non)Adiabatic Dynamics. Eur. Phys. J. B 2018, 91, 139. [Google Scholar] [CrossRef]
- Lopreore, C.L.; Wyatt, R.E. Quantum Wave Packet Dynamics with Trajectories. Phys. Rev. Lett. 1999, 82, 5190. [Google Scholar] [CrossRef] [Green Version]
- Wyatt, R.E. Quantum wavepacket dynamics with trajectories: Wavefunction synthesis along quantum paths. Chem. Phys. Lett. 1999, 313, 189–197. [Google Scholar] [CrossRef]
- Wyatt, R.E.; Na, K. Quantum trajectory analysis of multimode subsystem-bath dynamics. Phys. Rev. E 2001, 65, 016702. [Google Scholar] [CrossRef] [PubMed]
- Wyatt, R.E. Quantum Dynamics with Trajectories: Introduction to Quantum Hydrodynamics; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2005. [Google Scholar]
- Garashchuk, S.; Rassolov, V. Quantum Trajectory Dynamics Based on Local Approximations to the Quantum Potential and Force. J. Chem. Theory Comput. 2019, 15, 3906–3916. [Google Scholar] [CrossRef] [PubMed]
- Garashchuk, S.; Vazhappilly, T. Multidimensional Quantum Trajectory Dynamics in Imaginary Time with Approximate Quantum Potential. J. Phys. Chem. C 2010, 114, 20595–20602. [Google Scholar] [CrossRef]
- Wyatt, R.E.; Bittner, E.R. Quantum wave packet dynamics with trajectories: Implementation with adaptive Lagrangian grids. J. Chem. Phys. 2000, 119, 8898. [Google Scholar] [CrossRef]
- Hughes, K.H.; Wyatt, R.E. Wavepacket dynamics on dynamically adapting grids: Application of the equidistribution principle. Chem. Phys. Lett. 2002, 366, 336–342. [Google Scholar] [CrossRef]
- Kendrick, B.K. A new method for solving the quantum hydrodynamic equations of motion. J. Chem. Phys. 2003, 119, 5805. [Google Scholar] [CrossRef]
- Trahan, C.J.; Wyatt, R.E. An arbitrary Lagrangian-Eulerian approach to solving the quantum hydrodynamic equations of motion: Equidistribution with “smart” springs. J. Chem. Phys. 2003, 4784, 336–342. [Google Scholar] [CrossRef]
- Schild, A. Electronic quantum trajectories with quantum nuclei. arXiv 2021, arXiv:2109.13632v1. [Google Scholar]
- Tavernelli, I.; Curchod, B.F.E.; Rothlisberger, U. Nonadiabatic molecular dynamics with solvent effects: A LR-TDDFT QM/MM study of ruthenium (II) tris (bipyridine) in water. Chem. Phys. 2011, 391, 101–109. [Google Scholar] [CrossRef]
- Talotta, F.; Boggio-Pasqua, M.; González, L. Early relaxation dynamics in the photoswitchable trans-[RuCl(NO)(py)4]2+. Chem.: Eur. J. 2020, 26, 11522–11528. [Google Scholar] [CrossRef] [PubMed]
- Atkins, A.J.; Talotta, F.; Freitag, L.; Boggio-Pasqua, M.; González, L. Assessing Excited State Energy Gaps with Time-Dependent Density Functional Theory on Ru(II) Complexes. J. Chem. Theory Comput. 2017, 13, 4123–4145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garcáa, J.S.; Talotta, F.; Alary, F.; Dixon, I.M.; Heully, J.L.; Boggio-Pasqua, M. A Theoretical Study of the N to O Linkage Photoisomerization Efficiency in a Series of Ruthenium Mononitrosyl Complexes. Molecules 2017, 22, 1667. [Google Scholar]
- Ando, H.; Iuchi, S.; Sato, H. Theoretical study on ultrafast intersystem crossing of chromium(III) acetylacetonate. Chem. Phys. Lett. 2012, 535, 177–181. [Google Scholar] [CrossRef] [Green Version]
- Brahim, H.; Daniel, C. Structural and spectroscopic properties of Ir(III) complexes with phenylpyridine ligands: Absorption spectra without and with spin-orbit-coupling. Comput. Theo. Chem. 2014, 1040–1041, 219–229. [Google Scholar] [CrossRef]
- Hu, W.; Lendvay, G.; Maiti, B.; Schatz, G.C. Trajectory Surface Hopping Study of the O(3P) + Ethylene Reaction Dynamics. J. Phys. Chem. A 2008, 112, 2093–2103. [Google Scholar] [CrossRef]
- Fu, B.; Han, Y.C.; Bowman, J.M.; Angelucci, L.; Balucani, N.; Leonori, F.; Casavecchia, P. Intersystem crossing and dynamics in O(3P)+C2H4 multichannel reaction: Experiment validates theory. Proc. Natl. Acad. Sci. USA 2012, 109, 9733–9738. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Lendvay, G.; Maiti, B.; Schatz, G.C. Electronic Structure and Excited States of the Collision Reaction O(3P)+C2H4: A Multiconfigurational Perspective. J. Phys. Chem. A 2021, 125, 6075–6088. [Google Scholar]
- Talotta, F.; Morisset, S.; Rougeau, N.; Lauvergnat, D.; Agostini, F. Spin-Orbit Interactions in Ultrafast Molecular Processes. Phys. Rev. Lett. 2020, 124, 033001. [Google Scholar] [CrossRef]
- Talotta, F.; Morisset, S.; Rougeau, N.; Lauvergnat, D.; Agostini, F. Internal Conversion and Intersystem Crossing with the Exact Factorization. J. Chem. Theory Comput. 2020, 16, 4833–4848. [Google Scholar] [CrossRef]
- Min, S.K.; Abedi, A.; Kim, K.S.; Gross, E.K.U. Is the molecular Berry phase an artefact of the Born-Oppenheimer approximation? Phys. Rev. Lett. 2014, 113, 263004. [Google Scholar] [CrossRef] [PubMed]
- Requist, R.; Tandetzky, F.; Gross, E.K.U. Molecular geometric phase from the exact electron-nuclear factorization. Phys. Rev. A 2016, 93, 042108. [Google Scholar] [CrossRef] [Green Version]
- Requist, R.; Proetto, C.R.; Gross, E.K.U. Asymptotic analysis of the Berry curvature in the E ⊗ e Jahn-Teller model. Phys. Rev. A 2017, 96, 062503. [Google Scholar] [CrossRef] [Green Version]
- Agostini, F.; Curchod, B.F.E. When the exact factorization meets conical intersections. Eur. Phys. J. B 2018, 91, 141. [Google Scholar] [CrossRef]
- Ibele, L.M.; Curchod, B.F.E.; Agostini, F. A photochemical reaction in different theoretical representations. J. Phys. Chem. A 2022, 126, 1263–1281. [Google Scholar] [CrossRef]
- Hader, K.; Albert, J.; Gross, E.K.U.; Engel, V. Electron-nuclear wave-packet dynamics through a conical intersection. J. Chem. Phys. 2017, 146, 074304. [Google Scholar] [CrossRef]
- Requist, R.; Gross, E.K.U. Exact Factorization-Based Density Functional Theory of Electrons and Nuclei. Phys. Rev. Lett. 2016, 117, 193001. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Requist, R.; Gross, E.K.U. Density functional theory of electron transfer beyond the Born-Oppenheimer approximation: Case study of LiF. J. Chem. Phys. 2018, 148, 084110. [Google Scholar] [CrossRef] [Green Version]
- Schild, A.; Gross, E.K.U. Exact Single-Electron Approach to the Dynamics of Molecules in Strong Laser Fields. Phys. Rev. Lett. 2017, 118, 163202. [Google Scholar] [CrossRef] [Green Version]
- Kocák, J.; Schild, A. Many-electron effects of strong-field ionization described in an exact one-electron theory. Phys. Rev. Res. 2020, 2, 043365. [Google Scholar] [CrossRef]
- Gonze, X.; Zhou, J.S.; Reining, L. Variations on the “exact factorization” theme. Eur. Phys. J. B 2018, 91, 224. [Google Scholar] [CrossRef]
- Lacombe, L.; Maitra, N.T. Embedding via the Exact Factorization Approach. Phys. Rev. Lett. 2020, 124, 206401. [Google Scholar] [CrossRef] [PubMed]
- Requist, R.; Gross, E.K.U. Fock-Space Embedding Theory: Application to Strongly Correlated Topological Phases. Phys. Rev. Lett. 2021, 127, 116401. [Google Scholar] [CrossRef] [PubMed]
- Salas, L.D.; Arce, J.C. Potential energy surfaces in atomic structure: The role of Coulomb correlation in the ground state of helium. Phys. Rev. A 2017, 95, 022502. [Google Scholar] [CrossRef] [Green Version]
- Salas, L.D.; Zamora-Yusti, B.; Arce, J.C. Characterization of the continuous transition from atomic to molecular shape in the three-body Coulomb system. Phys. Rev. A 2022, 105, 012808. [Google Scholar] [CrossRef]
- Eich, F.G.; Agostini, F. The adiabatic limit of the exact factorization of the electron-nuclear wave function. J. Chem. Phys. 2016, 145, 054110. [Google Scholar] [CrossRef] [Green Version]
- Schild, A.; Agostini, F.; Gross, E.K.U. Electronic Flux Density beyond the Born-Oppenheimer Approximation. J. Phys. Chem. A 2016, 120, 3316. [Google Scholar] [CrossRef]
- Scherrer, A.; Agostini, F.; Sebastiani, D.; Gross, E.K.U.; Vuilleumier, R. On the mass of atoms in molecules: Beyond the Born-Oppenheimer approximation. Phys. Rev. X 2017, 7, 031035. [Google Scholar] [CrossRef]
- Scherrer, A.; Agostini, F.; Sebastiani, D.; Gross, E.K.U.; Vuilleumier, R. Nuclear velocity perturbation theory for vibrational circular dichroism: An approach based on the exact factorization of the electron-nuclear wave function. J. Chem. Phys. 2015, 143, 074106. [Google Scholar] [CrossRef] [Green Version]
- Requist, R.; Proetto, C.R.; Gross, E.K.U. Exact factorization-based density functional theory of electron-phonon systems. Phys. Rev. B 2019, 99, 165136. [Google Scholar] [CrossRef] [Green Version]
- Gossel, G.H.; Lacombe, L.; Maitra, N.T. On the numerical solution of the exact factorization equations. J. Chem. Phys. 2019, 150, 154112. [Google Scholar] [CrossRef] [PubMed]
- Lorin, E. Numerical analysis of the exact factorization of molecular time-dependent Schrödinger wavefunctions. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105627. [Google Scholar] [CrossRef]
- Hoffmann, N.M.; Appel, H.; Rubio, A.; Maitra, N.T. Light-matter interactions via the exact factorization approach. Eur. Phys. J. B 2018, 91, 180. [Google Scholar] [CrossRef]
- Yuen-Zhou, J.; Xiong, W.; Shegai, T. Polariton chemistry: Molecules in cavities and plasmonic media. J. Chem. Phys. 2022, 156, 030401. [Google Scholar] [CrossRef] [PubMed]
- Galego, J.; Garcia-Vidal, F.J.; Feist, J. Cavity-Induced Modifications of Molecular Structure in the Strong-Coupling Regime. Phys. Rev. X 2015, 5, 041022. [Google Scholar] [CrossRef] [Green Version]
- Lacombe, L.; Hoffmann, N.M.; Maitra, N.T. Exact Potential Energy Surface for Molecules in Cavities. Phys. Rev. Lett. 2019, 123, 083201. [Google Scholar] [CrossRef] [Green Version]
- Martinez, P.; Rosenzweig, B.; Hoffmann, N.M.; Lacombe, L.; Maitra, N.T. Case studies of the time-dependent potential energy surface for dynamics in cavities. J. Chem. Phys. 2021, 154, 014102. [Google Scholar] [CrossRef]
- Hoffmann, N.M.; Schäfer, C.; Rubio, A.; Kelly, A.; Appel, H. Capturing vacuum fluctuations and photon correlations in cavity quantum electrodynamics with multitrajectory Ehrenfest dynamics. Phys. Rev. A 2019, 99, 063819. [Google Scholar] [CrossRef] [Green Version]
- Rosenzweig, B.; Hoffmann, N.M.; Lacombe, L.; Maitra, N.T. Analysis of the classical trajectory treatment of photon dynamics for polaritonic phenomena. J. Chem. Phys. 2022, 156, 054101. [Google Scholar] [CrossRef]
- Flick, J.; Ruggenthaler, M.; Appel, H.; Rubio, A. Atoms and molecules in cavities, from weak to strong coupling in quantum-electrodynamics (QED) chemistry. Proc. Natl. Acad. Sci. USA 2017, 114, 3026–3034. [Google Scholar] [CrossRef] [Green Version]
- Cederbaum, L.S. The exact wavefunction of interacting N degrees of freedom as a product of N single-degree-of-freedom wavefunctions. Chem. Phys. 2015, 457, 129. [Google Scholar] [CrossRef]
- Scherrer, A.; Vuilleumier, R.; Sebastiani, D. Vibrational circular dichroism from ab initio molecular dynamics and nuclear velocity perturbation theory in the liquid phase. J. Chem. Phys. 2016, 145, 084101. [Google Scholar] [CrossRef] [PubMed]
- Scherrer, A.; Vuilleumier, R.; Sebastiani, D. Nuclear Velocity Perturbation Theory of Vibrational Circular Dichroism. J. Chem. Theory Comput. 2013, 9, 5305–5312. [Google Scholar] [CrossRef]
- Diestler, D.J.; Kenfack, A.; Manz, J.; Paulus, B.; Pérez-Torres, J.F.; Pohl, V. Computation of the Electronic Flux Density in the Born-Oppenheimer Approximation. J. Phys. Chem. A 2013, 117, 8519–8527. [Google Scholar] [CrossRef]
- Diestler, D.J. Beyond the Born-Oppenheimer Approximation: A Treatment of Electronic Flux Density in Electronically Adiabatic Molecular Processes. J. Phys. Chem. A 2013, 117, 4698–4708. [Google Scholar] [CrossRef] [PubMed]
- Arce, J.C. Unification of the conditional probability and semiclassical interpretations for the problem of time in quantum theory. Phys. Rev. A 2012, 85, 042108. [Google Scholar] [CrossRef] [Green Version]
- Schild, A. Time in quantum mechanics: A fresh look at the continuity equation. Phys. Rev. A 2018, 98, 052113. [Google Scholar] [CrossRef] [Green Version]
- Kulander, K.C.; Mies, F.H.; Schafer, K.J. Model for studies of laser-induced nonlinear processes in molecules. Phys. Rev. A 1996, 53, 2562–2570. [Google Scholar] [CrossRef]
- Chelkowski, S.; Foisy, C.; Bandrauk, A.D. Electron-nuclear dynamics of multiphoton H2+ dissociative ionization in intense laser fields. Phys. Rev. A 1998, 57, 1176–1185. [Google Scholar] [CrossRef]
- Walsh, T.D.G.; Ilkov, F.A.; Chin, S.L.; Châteauneuf, F.; Nguyen-Dang, T.T.; Chelkowski, S.; Bandrauk, A.D.; Atabek, O. Laser-induced processes during the Coulomb explosion of H2 in a Ti-sapphire laser pulse. Phys. Rev. A 1998, 58, 3922–3933. [Google Scholar] [CrossRef]
- Lein, M.; Kreibich, T.; Gross, E.K.U.; Engel, V. Strong-field ionization dynamics of a model H2 molecule. Phys. Rev. A 2002, 65, 033403. [Google Scholar] [CrossRef]
- McLachlan, A.D. A variational solution of the time-dependent Schrodinger equation. Mol. Phys. 1964, 8, 39–44. [Google Scholar] [CrossRef]
- Tully, J.C. Mixed quantum-classical dynamics. Faraday Discuss. 1998, 110, 407. [Google Scholar] [CrossRef]
- Kelkensberg, F.; Sansone, G.; Ivanov, M.Y.; Vrakking, M. A semi-classical model of attosecond electron localization in dissociative ionization of hydrogen. Phys. Chem. Chem. Phys. 2011, 13, 8647–8652. [Google Scholar] [CrossRef]
- Sansone, G.; Kelkensberg, F.; Pérez-Torres, J.F.; Morales, F.; Kling, M.F.; Siu, W.; Ghafur, O.; Johnsson, P.; Swoboda, M.; Benedetti, E.; et al. Electron localization following attosecond molecular photoionization. Nature 2010, 465, 763–766. [Google Scholar] [CrossRef] [Green Version]
- He, F.; Ruiz, C.; Becker, A. Control of Electron Excitation and Localization in the Dissociation of H2+ and Its Isotopes Using Two Sequential Ultrashort Laser Pulses. Phys. Rev. Lett. 2007, 99, 083002. [Google Scholar] [CrossRef] [Green Version]
- Zuo, T.; Bandrauk, A.D. Charge-resonance-enhanced ionization of diatomic molecular ions by intense lasers. Phys. Rev. A 1995, 52, R2511. [Google Scholar] [CrossRef]
- Chelkowski, S.; Bandrauk, A.D. Two-step Coulomb explosions of diatoms in intense laser fields. J. Phys. B: At. Mol. Opt. Phys. 1995, 28, L723–L731. [Google Scholar] [CrossRef]
- Chelkowski, S.; Zuo, T.; Atabek, O.; Bandrauk, A.D. Dissociation, ionization, and Coulomb explosion of H2+ in an intense laser field by numerical integration of the time-dependent Schrödinger equation. Phys. Rev. A 1995, 52, 2977. [Google Scholar] [CrossRef]
- Seideman, T.; Ivanov, M.Y.; Corkum, P.B. Role of Electron Localization in Intense-Field Molecular Ionization. Phys. Rev. Lett. 1995, 75, 2819–2822. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Légaré, F. Enhanced Ionization of Molecules in Intense Laser Fields. In Progress in Ultrafast Intense Laser Science VIII; Yamanouchi, K., Nisoli, M., Hill, W.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 29–46. [Google Scholar] [CrossRef] [Green Version]
- Zuo, T.; Chelkowski, S.; Bandrauk, A.D. Harmonic generation by the H2+ molecular ion in intense laser fields. Phys. Rev. A 1993, 48, 3837–3844. [Google Scholar] [CrossRef] [PubMed]
- Takemoto, N.; Becker, A. Multiple Ionization Bursts in Laser-Driven Hydrogen Molecular Ion. Phys. Rev. Lett. 2010, 105, 203004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takemoto, N.; Becker, A. Time-resolved view on charge-resonance-enhanced ionization. Phys. Rev. A 2011, 84, 023401. [Google Scholar] [CrossRef] [Green Version]
- Beylerian, C.; Saugout, S.; Cornaggia, C. Non-sequential double ionization of H2 using ultrashort 10 fs laser pulses. J. Phys. B: At. Mol. Opt. Phys. 2006, 39, L105–L112. [Google Scholar] [CrossRef]
- Bocharova, I.; Karimi, R.; Penka, E.F.; Brichta, J.P.; Lassonde, P.; Fu, X.; Kieffer, J.C.; Bandrauk, A.D.; Litvinyuk, I.; Sanderson, J.; et al. Charge Resonance Enhanced Ionization of CO2 Probed by Laser Coulomb Explosion Imaging. Phys. Rev. Lett. 2011, 107, 063201. [Google Scholar] [CrossRef] [Green Version]
- Légaré, F.; Litvinyuk, I.V.; Dooley, P.W.; Quéré, F.; Bandrauk, A.D.; Villeneuve, D.M.; Corkum, P.B. Time-Resolved Double Ionization with Few Cycle Laser Pulses. Phys. Rev. Lett. 2003, 91, 093002. [Google Scholar] [CrossRef]
- Curchod, B.F.E.; Agostini, F.; Tavernelli, I. CT-MQC—A Coupled-Trajectory Mixed Quantum/Classical method including nonadiabatic quantum coherence effects. Eur. Phys. J. B 2018, 91, 168. [Google Scholar] [CrossRef] [Green Version]
- Marsili, E.; Olivucci, M.; Lauvergnat, D.; Agostini, F. Quantum and Quantum-Classical Studies of the Photoisomerization of a Retinal Chromophore Model. J. Chem. Theory Comput. 2020, 16, 6032–6048. [Google Scholar] [CrossRef]
- Filatov, M.; Min, S.K.; Kim, K.S. Non-adiabatic dynamics of ring opening in cyclohexa-1,3-diene described by an ensemble density-functional theory method. Mol. Phys. 2019, 117, 1128–1141. [Google Scholar] [CrossRef]
- Filatov, M.; Paolino, M.; Min, S.K.; Kim, K.S. Fulgides as Light-Driven Molecular Rotary Motors: Computational Design of a Prototype Compound. J. Phys. Chem. Lett. 2018, 9, 4995–5001. [Google Scholar] [CrossRef]
- Filatov, M.; Paolino, M.; Min, S.K.; Choi, C.H. Design and photoisomerization dynamics of a new family of synthetic 2-stroke light driven molecular rotary motors. Chem. Commun. 2019, 55, 5247–5250. [Google Scholar] [CrossRef] [PubMed]
- Filatov, M.; Min, S.K.; Choi, C.H. Theoretical modelling of the dynamics of primary photoprocess of cyclopropanone. Phys. Chem. Chem. Phys. 2019, 21, 2489–2498. [Google Scholar] [CrossRef] [PubMed]
- Vindel-Zandbergen, P.; Ibele, L.M.; Ha, J.K.; Min, S.K.; Curchod, B.F.E.; Maitra, N.T. Study of the Decoherence Correction Derived from the Exact Factorization Approach for Nonadiabatic Dynamics. J. Chem. Theory Comput. 2021, 17, 3852–3862. [Google Scholar] [CrossRef] [PubMed]
- Vindel-Zandbergen, P.; Matsika, S.; Maitra, N.T. Exact-Factorization-Based Surface Hopping for Multistate Dynamics. J. Phys. Chem. Lett. 2022, 13, 1785–1790. [Google Scholar] [CrossRef]
- Tully, J.C. Molecular dynamics with electronic transitions. J. Chem. Phys. 1990, 93, 1061. [Google Scholar] [CrossRef]
- Lu, J.; Zhoud, Z. Frozen Gaussian Approximation with surface hopping for mixed quantum-classical dynamics: A mathematical justification of fewest switches surface hopping algorithms. Math. Comp. 2018, 87, 2189–2232. [Google Scholar] [CrossRef]
- Wang, L.; Akimov, A.; Prezhdo, O.V. Recent Progress in Surface Hopping: 2011–2015. J. Phys. Chem. Lett. 2016, 7, 2100. [Google Scholar] [CrossRef]
- Subotnik, J.E.; Jain, A.; Landry, B.; Petit, A.; Ouyang, W.; Bellonzi, N. Understanding the Surface Hopping View of Electronic Transitions and Decoherence. Ann. Rev. Phys. Chem. 2016, 67, 387–417. [Google Scholar] [CrossRef]
- Gossel, G.H.; Agostini, F.; Maitra, N.T. Coupled-Trajectory Mixed Quantum-Classical Algorithm: A Deconstruction. J. Chem. Theory Comput. 2018, 14, 4513–4529. [Google Scholar] [CrossRef]
- Agostini, F. An exact-factorization perspective on quantum-classical approaches to excited-state dynamics. Eur. Phys. J. B 2018, 91, 143. [Google Scholar] [CrossRef]
- Agostini, F.; Marsili, E.; Talotta, F. G-CTMQC. 2021. Available online: https://gitlab.com/agostini.work/g-ctmqc (accessed on 13 May 2022).
- Lauvergnat, D. ModelLib. 2018. Available online: https://github.com/lauvergn/QuantumModelLib/tree/OOP_branch (accessed on 13 May 2022).
- Kim, T.I.; Ha, J.K.; Min, S.K. Coupled- and Independent-Trajectory Approaches Based on the Exact Factorization Using the PyUNIxMD Package. Top. Curr. Chem. 2022, 380, 8. [Google Scholar] [CrossRef] [PubMed]
- Ha, J.K.; Min, S.K. Independent Trajectory Mixed Quantum-Classical Approaches Based on the Exact Factorization. J. Chem. Phys. 2022, 156, 174109. [Google Scholar] [CrossRef] [PubMed]
- Barbatti, M. Velocity Adjustment in Surface Hopping: Ethylene as a Case Study of the Maximum Error Caused by Direction Choice. J. Chem. Theor. Comput. 2021, 17, 3010–3018. [Google Scholar] [CrossRef] [PubMed]
- Carof, A.; Giannini, S.; Blumberger, J. Detailed balance, internal consistency, and energy conservation in fragment orbital-based surface hopping. J. Chem. Phys. 2017, 147, 214113. [Google Scholar] [CrossRef]
- Tang, D.; Shen, L.; Fang, W.h. Evaluation of Mixed Quantum-Classical Molecular Dynamics on cis-Azobenzene Photoisomerization. Phys. Chem. Chem. Phys. 2021, 23, 13951–13964. [Google Scholar] [CrossRef]
- Hammes-Schiffer, S.; Tully, J.C. Proton transfer in solution: Molecular dynamics with quantum transitions. J. Chem. Phys. 1994, 101, 4657–4667. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villaseco Arribas, E.; Agostini, F.; Maitra, N.T. Exact Factorization Adventures: A Promising Approach for Non-Bound States. Molecules 2022, 27, 4002. https://doi.org/10.3390/molecules27134002
Villaseco Arribas E, Agostini F, Maitra NT. Exact Factorization Adventures: A Promising Approach for Non-Bound States. Molecules. 2022; 27(13):4002. https://doi.org/10.3390/molecules27134002
Chicago/Turabian StyleVillaseco Arribas, Evaristo, Federica Agostini, and Neepa T. Maitra. 2022. "Exact Factorization Adventures: A Promising Approach for Non-Bound States" Molecules 27, no. 13: 4002. https://doi.org/10.3390/molecules27134002
APA StyleVillaseco Arribas, E., Agostini, F., & Maitra, N. T. (2022). Exact Factorization Adventures: A Promising Approach for Non-Bound States. Molecules, 27(13), 4002. https://doi.org/10.3390/molecules27134002