Coordination Chemistry of Nucleotides and Antivirally Active Acyclic Nucleoside Phosphonates, including Mechanistic Considerations †
Abstract
:| Table of Contents |
| 1. Some General Considerations |
| 2. Why Is the Antiviral PMEApp4− a Better Substrate for Nucleic Acid Polymerases than (2’-Deoxy)Adenosine 5′-Triphosphate (dATP4−/ATP4−)? |
| 3. Modelling the Interactions of Metal Ions with the Ether Oxygen of PMEA2− |
| 4. The N3 versus N7 Metal Ion-Binding Mode in Acyclic Nucleoside Phosphonates (ANPs) Containing a Purine Moiety |
| 4.1. The Metal Ion-Coordinating Properties of 9-[2-(Phosphonomethoxy)ethyl]-2-aminopurine (PME2AP) |
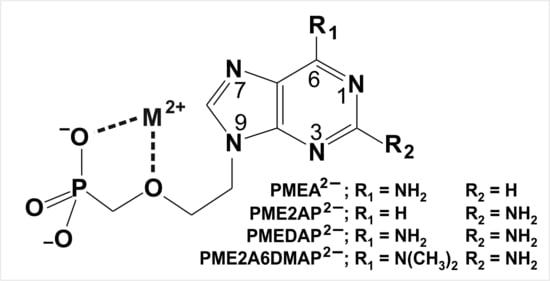
| 4.2. The Metal Ion-Coordinating Properties of 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA) |
| 4.3. The Metal Ion-Coordinating Properties of 9-[2-(Phosphonomethoxy)ethyl]-2,6-diaminopurine (PMEDAP) |
| 5. The Various Inhibiting Substituents in 9-[2-(Phosphonomethoxy)ethyl]-2-amino-6-dimethylaminopurine (PME2A6DMAP) Lead to PME-Like Metal Ion-Binding Properties |
| 6. Mechanistic Considerations on the Metal Ion-Promoted Dephosphorylation of ATP |
| 6.1. Effects of Increasing Amounts of Metal Ions on the Dephosphorylation Rate |
| 6.2. Oligo Formation and the Effect of Self-Association on the Dephosphorylation Rate |
| 6.3. Promotion of ATP Hydrolysis by AMP and PMEA, and Inhibition of the Reactivity by Adenine-Altered AMP Relatives |
| 6.4. Matrix-Assisted Self-Association and Its Significance for Cell Organelles with High ATP Concentrations |
| 7. Solution Structures of Mixed-Ligand Complexes Containing ATP4− and Related Ligands |
| 7.1. Ligands Containing a Ribose Residue with a Phosphate Group |
| 7.2. Acyclic Nucleoside Phosphonates. Cu(arm)(PMEA) as an Example with Intramolecular Stack Formation |
| 8. The Effect of a Change in Solvent Polarity on the Stability and Structure of Binary and Ternary Complexes |
| 8.1. The Dianion of (Phosphonomethoxy)ethane (PME2−) as an Example of a Polar O-Ligand. The Properties of Cu(PME) Are Largely as Expected |
| 8.2. Nitrogen Donor Sites Are Especially Sensitive to Polarity Changes of the Solvent |
| 8.3. Competing Solvent Effects on N- versus O-Sites in the Same Ligand and Its Bearing on Complex Stability |
| 9. Discussion |
| 10. Conclusions and Outlook |
| Abbreviations and Definitions |
| References |
1. Some General Considerations


2. Why Is the Antiviral PMEApp4− a Better Substrate for Nucleic Acid Polymerases than (2′-Deoxy)Adenosine 5′-Triphosphate (dATP4−/ATP4−)?
- -
- PMEA has an anti-like conformation just as AMP.
- -
- The phosphonate group owns an increased basicity and therefore also an enhanced metal ion affinity, and
- -
- formation of a 5-membered chelate involving the ether oxygen favors coordination at the Pα group.
- These will be discussed below.
3. Modelling the Interactions of Metal Ions with the Ether Oxygen of PMEA2−

4. The N3 versus N7 Metal Ion-Binding Mode in Acyclic Nucleoside Phosphonates (ANPs) Containing a Purine Moiety
4.1. The Metal Ion-Coordinating Properties of 9-[2-(Phosphonomethoxy)ethyl]-2-aminopurine (PME2AP)
4.2. The Metal Ion-Coordinating Properties of 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA)
4.3. The Metal Ion-Coordinating Properties of 9-[2-(Phosphonomethoxy)ethyl]-2,6-diaminopurine (PMEDAP)
5. The Various Inhibiting Substituents in 9-[2-(Phosphonomethoxy)ethyl]-2-amino-6-dimethylaminopurine (PME2A6DMAP) Lead to PME-Like Metal Ion-Binding Properties
6. Mechanistic Considerations on the Metal Ion-Promoted Dephosphorylation of ATP
6.1. Effects of Increasing Amounts of Metal Ions on the Dephosphorylation Rate
6.2. Oligo Formation and the Effect of Self-Association on the Dephosphorylation Rate
6.3. Promotion of ATP Hydrolysis by AMP and PMEA, and Inhibition of the Reactivity by Adenine-Altered AMP Relatives
6.4. Matrix-Assisted Self-Association and Its Significance for Cell Organelles with High ATP Concentrations
“In fact, one is tempted to speculate further: Considering that extracellular ATP is universally employed in cell-cell communication, particularly in synaptic transmission [119] (references therein) and if one recalls that electrons may migrate over long distances in DNA [120,121], one may propose that one way to achieve information transfer (and there are others) occurs in the following way. Assuming that, say six ATPs are lined up to form a stack covering a distance of approximately 20 Å one could imagine that at one end of the stack a metal ion (Fe2+, Mn2+, Cu+) is oxidized to a higher charged state (Fe3+, Mn3+, Cu2+) by a redox reaction and that this oxidized ion triggers hydrolysis of the triphosphate residue and that the electron travels through the stack to an acceptor at its other end [111]. This is depicted in a simplified fashion in Figure 13. That oxidation of a divalent metal ion (Mn2+) to a trivalent one (Mn3+) dramatically enhances the dephosphorylation rate of nucleoside 5′-triphosphates is known [11,73].”
7. Solution Structures of Mixed-Ligand Complexes Containing ATP4− and Related Ligands
7.1. Ligands Containing a Ribose Residue with a Phosphate Group


7.2. Acyclic Nucleoside Phosphonates: Cu(arm)(PMEA) as an Example with Intramolecular Stack Formation

| M2+ | log
(Equations (8), and (28)) a | log
(Analogous to Equation (25)) b | log ΔPME (Equation (12)) c | KI (Equations (6), (9) and (29)) c | % M(PME)cl (Equation (14)) c,d |
|---|---|---|---|---|---|
| Cu2+ | 3.73 ± 0.03 | 3.25 ± 0.06 | 0.48 ± 0.07 | 2.02 ± 0.47 | 67 ± 5 |
| Cu(bpy)2+ | 3.86 ± 0.03 | 3.27 ± 0.07 | 0.59 ± 0.08 | 2.89 ± 0.68 | 74 ± 5 |
| Cu(phen)2+ | 3.90 ± 0.04 | 3.28 ± 0.06 | 0.62 ± 0.07 | 3.17± 0.69 | 76 ± 4 |
| M2+ | log [Equation (28)] a | log [Equation (25)] b | log ΔPMEA [Equation (12)] c | KI = KI/tot [Equation (29)] c | % Cu(arm)(PMEA)int/tot [Equation (29); analog. to Equation (14)] |
| Cu(bpy)2+ | 4.70 ± 0.02 | 3.22 ± 0.07 | 1.48 ± 0.07 | 29.20 ± 4.87 | 96.69 ± 0.53 |
| Cu(phen)2+ | 4.97 ± 0.03 | 3.23± 0.06 | 1.74 ± 0.07 | 53.95 ± 8.86 | 98.18 ± 0.29 |
8. The Effect of a Change in Solvent Polarity on the Stability and Structure of Binary and Ternary Complexes
8.1. The Dianion of (Phosphonomethoxy)ethane (PME2−) as an Example of a Polar O-Ligand. The Properties of Cu(PME) Are Largely as Expected
8.2. Nitrogen Donor Sites Are Especially Sensitive to Polarity Changes of the Solvent
8.3. Competing Solvent Effects on N- versus O-Sites in the Same Ligand and Its Bearing on Complex Stability
9. Discussion
10. Conclusions and Outlook
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Definitions
| aa | amino acid |
| AcP2− | acetyl phosphate (Figure 20) |
| AIDS | acquired immune deficiency syndrome |
| AMP·NO2− | adenosine 5′-monophosphate N(1)-oxide (Figure 12) |
| AMP2− | adenosine 5′-monophosphate (Figure 3) |
| ε-AMP2− | 1,N6-ethenoadenosine 5′-monophosphate (Figure 12) |
| AnP2− | acetonylphosphonate (Figure 20) |
| arm | heteroaromatic nitrogen base, e.g., bpy or phen |
| ATP4− | adenosine 5′-triphosphate |
| bpy | 2,2-bipyridine |
| DHAP2− | dihydroxyacetone phosphate (Figure 20) |
| dien | diethylenetriamine = 1,4,7-triazaheptane |
| DNA | deoxyribonucleic acid |
| dPMEA2− | dianion of 9-(4-phosphonobutyl)adenine = 3′-deoxa-PMEA2− |
| G1P2− | glycerol 1-phosphate (= α-glycerophosphate; in many biochemistry texts also designated as glycerol 3-phosphate) (Figure 20) |
| HIV | human immunodeficiency virus |
| L2− | any phosph(on)ate ligand (R-) |
| M2+ | any divalent metal ion (in a few instances also Cu(bpy)2+ and Cu(phen)2+ are represented by this abbreviation) |
| N | nucleophile |
| NDP3− | nucleoside 5′-diphosphate |
| NMP2− | nucleoside 5′-monophosphate |
| NTP4− | nucleoside 5′-triphosphate |
| PEEA2− | dianion of 9-[2-(2-phosphonoethoxy)ethyl]adenine |
| phen | 1,10-phenanthroline |
| PME2− | dianion of (phosphonomethoxy)ethane (=ethoxymethanephosphonate) [Equation (5)] |
| PMEA2− | dianion of 9-[2-(phosphonomethoxy)ethyl]adenine (Figure 3) |
| RNA | ribonucleic acid |
| TuMP2− | tubercidin 5′-monophosphate = 7-deaza-AMP2− (Figure 12) |
References
- Sigel, A.; Sigel, H. (Eds.) Interactions of Metal Ions with Nucleotides, Nucleid Acids, and Their Constituents. In Metal Ions in Biological Systems; Marcel Dekker, Inc.: New York, NY, USA; Basel, Switzerland; Hong Kong, China, 1996; Volume 32, pp. 1–814. [Google Scholar]
- Sigel, A.; Sigel, H.; Sigel, R.K.O. (Eds.) Structural and Catalytic Roles of Metal Ions in RNA. In Metal Ions in Life Sciences; Royal Society of Chemistry: Cambridge, UK, 2011; Volume 9, pp. 1–391. [Google Scholar]
- Sigel, A.; Sigel, H.; Sigel, R.K.O. (Eds.) Interplay Between Metal Ions and Nucleic Acids. In Metal Ions in Life Sciences; Springer: Dordrecht, The Netherlands, 2012; Volume 10, pp. 1–351. [Google Scholar]
- Aoki, K. General Conclusions from Solid State Studies of Nucleotide-Metal Ion Complexes. Met. Ions Biol. Syst. 1996, 32, 91–134. [Google Scholar]
- Martin, R.B.; Mariam, Y.H. Interactions between Metal Ions and Nucleic Bases, Nucleosides, and Nucleotides in Solution. Met. Ions Biol. Syst. 1979, 8, 57–124. [Google Scholar]
- Tribolet, R.; Sigel, H. Self-Association and Protonation of Adenosine 5′-Monophosphate in Comparison with Its 2′- and 3′-Analogues and Tubercidin 5′-Monophosphate (7-deaza-AMP). Eur. J. Biochem. 1987, 163, 353–363. [Google Scholar] [CrossRef] [PubMed]
- Davies, D.B.; Rajani, P.; Sadikot, H. Determination of Glycosidic Bond Conformations of Pyrimidine Nucleosides and Nucleotides Using Vicinal Carbon–Proton Coupling Constants. J. Chem. Soc. Perkin Trans. 1985, 2, 279–285. [Google Scholar] [CrossRef]
- Pedley, A.M.; Benkovic, S.J. A New View into the Regulation of Purine Metabolism—The Purinosome. Trends Biochem. Sci. 2017, 42, 141–154. [Google Scholar] [CrossRef] [Green Version]
- Kanehisa, M.; Goto, S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef]
- Sigel, H.; Amsler, P.E. Hydrolysis of Nucleoside Phosphates. VI. On the Mechanism of the Metal Ion Promoted Dephosphorylation of Purine Nucleoside 5′-Triphosphates. J. Am. Chem. Soc. 1976, 98, 7390–7400. [Google Scholar] [CrossRef]
- Sigel, H. Mechanistic Aspects of the Metal Ion Promoted Hydrolysis of Nucleoside 5′-Triphosphates (NTPs). Coord. Chem. Rev. 1990, 100, 453–539. [Google Scholar] [CrossRef]
- Mildvan, A.S. Role of Magnesium and Other Divalent Cations in ATP-Utilizing Enzymes. Magnesium 1987, 6, 28–33. [Google Scholar]
- Sträter, N.; Lipscomb, W.N.; Klabunde, T.; Krebs, B. Two-Metal Ion Catalysis in Enzymatic Acyl- and Phosphoryl-Transfer Reactions. Angew. Chemie Int. Ed. Engl. 1996, 35, 2024–2055. [Google Scholar] [CrossRef]
- Sigel, H.; Hofstetter, F.; Martin, R.B.; Milburn, R.M.; Scheller-Krattiger, V.; Scheller, K.H. General Considerations on Transphosphorylations: Mechanism of the Metal Ion Facilitated Dephosphorylation of Nucleoside 5′-Triphosphates, Including Promotion of ATP Dephosphorylation by Addition of Adenosine 5′-Monophosphate. (Hydrolysis of Nucleoside Phosphates. Part 8). J. Am. Chem. Soc. 1984, 106, 7935–7946. [Google Scholar]
- Steitz, T.A. DNA Polymerases: Structural Diversity and Common Mechanisms. J. Biol. Chem. 1999, 274, 17395–17398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brautigam, C.A.; Steitz, T.A. Structural and Functional Insights Provided by Crystal Structures of DNA Polymerases and Their Substrate Complexes. Curr. Opin. Struct. Biol. 1998, 8, 54–63. [Google Scholar] [CrossRef]
- Pelletier, H.; Sawaya, M.R.; Kumar, A.; Wilson, S.H.; Kraut, J. Structures of Ternary Complexes of Rat DNA Polymerase Beta, a DNA Template-Primer, and ddCTP. Science 1994, 264, 1891–1903. [Google Scholar] [CrossRef]
- Pelletier, H. Polymerase Structures and Mechanism. Science 1994, 266, 2025–2026. [Google Scholar] [CrossRef] [Green Version]
- Pelletier, H.; Sawaya, M.R.; Wolfle, W.; Wilson, S.H.; Kraut, J. Crystal Structures of Human DNA Polymerase Beta Complexed with DNA: Implications for Catalytic Mechanism, Processivity, and Fidelity. Biochemistry 1996, 35, 12762–12777. [Google Scholar] [CrossRef]
- Sigel, H.; Song, B.; Blindauer, C.A.; Kapinos, L.E.; Gregáň, F.; Prónayová, N. Why is the Antiviral Nucleotide Analogue 9-[2-(Phosphonomethoxy)ethyl]adenine in Its Diphosphorylated Form (PMEApp4−) Initially a Better Substrate for Polymerases than (2′-Deoxy)adenosine 5′-Triphosphate (dATP4−/ATP4−)? Considerations on the Mechanism of Polymerases. Chem. Commun. 1999, 743–744. [Google Scholar] [CrossRef]
- Sigel, H. Adenosine 5′-Triphosphate (ATP4−): Aspects of the Coordination Chemistry of a Multi-Talented Biological Substrate. Pure Appl. Chem. 2004, 76, 375–388. [Google Scholar] [CrossRef] [Green Version]
- Sigel, H. Metal Ion Complexes of Antivirally Active Nucleotide Analogues. Conclusions Regarding Their Biological Action. Chem. Soc. Rev. 2004, 33, 191–200. [Google Scholar] [CrossRef]
- Sigel, H.; Griesser, R. Nucleoside 5′-Triphosphates: Self-Association, Acid-Base, and Metal Ion-Binding Properties in Solution. Chem. Soc. Rev. 2005, 34, 875–900. [Google Scholar] [CrossRef]
- Tari, L.W.; Matte, A.; Goldie, H.; Delbaere, L.T.J. Mg2+–Mn2+ Clusters in Enzyme-Catalyzed Phosphoryl-Transfer Reactions. Nature Struct. Biol. 1997, 4, 990–994. [Google Scholar] [CrossRef] [PubMed]
- Sigel, H. Metal Ion-Binding Properties of the Antiviral Nucleotide Analogue 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA). Why Is Its Diphosphorylated Form, PMEApp4−, Initially a Better Substrate for Nucleic Acid Polymerases than (2′-Deoxy)-Adenosine 5′-Triphosphate (dATP4−/ATP4−)? Pure Appl. Chem. 1999, 71, 1727–1740. [Google Scholar]
- Freisinger, E.; Grollman, A.P.; Miller, H.; Kisker, C. Lesion (In)tolerance Reveals Insights into DNA Replication Fidelity. EMBO J. 2004, 23, 1494–1505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barré-Sinoussi, F.; Chermann, J.C.; Rey, F.; Nugeyre, M.T.; Chamaret, S.; Gruest, J.; Dauguet, C.; Axler-Blin, C.; Vézinet-Brun, F.; Rouzioux, C.; et al. Isolation of a T-Lymphotropic Retrovirus from a Patient at Risk for Acquired Immune Deficiency Syndrome (AIDS). Science 1983, 220, 868–871. [Google Scholar] [CrossRef] [Green Version]
- Popovic, M.; Sarngadharan, M.G.; Read, E.; Gallo, R.C. Detection, Isolation, and Continuous Production of Cytopathic Retroviruses (HTLV-III) from Patients with AIDS and Pre-AIDS. Science 1984, 224, 497–500. [Google Scholar] [CrossRef]
- Gallo, R.C.; Montagnier, L. AIDS in 1988. Sci. Am. 1988, 259, 41–48. [Google Scholar] [CrossRef]
- De Clercq, E. New Perspectives for the Treatment of HIV Infections. Coll. Czech. Chem. Commun. 1998, 63, 449–479. [Google Scholar] [CrossRef]
- Song, B.; Sigel, R.K.O.; Sigel, H. Acid-Base Properties of Adenosine 5′-O-Thiomonophosphate in Aqueous Solution. Chem. Eur. J. 1997, 3, 29–33. [Google Scholar] [CrossRef]
- Sigel, R.K.O.; Song, B.; Sigel, H. Stabilities and Structures of Metal Ion Complexes of Adenosine-5′-O-Thiomonophosphate (AMPS2−) in Comparison with Those of Its Parent Nucleotide (AMP2−) in Aqueous Solution. J. Am. Chem. Soc. 1997, 119, 744–755. [Google Scholar] [CrossRef]
- Sigel, A.; Operschall, B.P.; Sigel, R.K.O.; Sigel, H. Metal Ion Complexes of Nucleoside Phosphorothioates Reflecting the Ambivalent Properties of Lead(II). New J. Chem. 2018, 42, 7551–7559. [Google Scholar] [CrossRef] [Green Version]
- Holý, A.; De Clercq, E.; Votruba, I. Phosphonylmethyl Ethers of Nucleosides and Their Acyclic Analogues. ACS Symp. Ser. 1989, 401, 51–71. [Google Scholar]
- Holý, A. Acyclic Nucleoside and Nucleotide Analogues. A New Class of Antivirals. Il Farmaco 1991, 46, 141–146. [Google Scholar] [PubMed]
- Blindauer, C.A.; Holý, A.; Dvořáková, A.; Sigel, H. Solution Properties of Antiviral Adenine-Nucleotide Analogues. The Acid-Base Properties of 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA) and of Its N1, N3, and N7 Deaza Derivatives in Aqueous Solution. J. Chem. Soc. Perkin Trans. 2 1997, 11, 2353–2363. [Google Scholar] [CrossRef]
- Schwalbe, C.H.; Thomson, W.; Freeman, S. Structural Studies on Bio-Active Molecules. Part 17. Crystal Structure of 9-(2′-phosphonomethoxyethyl)adenine (PMEA). J. Chem. Soc. Perkin Trans. 1 1991, 1348–1349. [Google Scholar] [CrossRef]
- Aoki, K.; Murayama, K. Nucleic Acid-Metal Ion Interactions in the Solid State. Met. Ions Life Sci. 2021, 10, 43–102. [Google Scholar]
- Sigel, H.; Zuberbühler, A.D.; Yamauchi, O. Comments on Potentiometric pH Titrations and the Relationship between pH-Meter Reading and Hydrogen Ion Concentration. Anal. Chim. Acta 1991, 255, 63–72. [Google Scholar] [CrossRef]
- Saha, A.; Saha, N.; Ji, L.-N.; Zhao, J.; Gregáň, F.; Sajadi, S.A.A.; Song, B.; Sigel, H. Stability of Metal Ion Complexes Formed with Methyl Phosphate and Hydrogen Phosphate. J. Biol. Inorg. Chem. 1996, 1, 231–238. [Google Scholar] [CrossRef]
- Sigel, H.; Da Costa, C.P.; Song, B.; Carloni, P.; Gregáň, F. Stability and Structure of Metal Ion Complexes Formed in Solution with Acetyl Phosphate and Acetonylphosphonate: Quantification of Isomeric Equilibria. J. Am. Chem. Soc. 1999, 121, 6248–6257. [Google Scholar] [CrossRef]
- Fernández-Botello, A.; Griesser, R.; Holý, A.; Moreno, V.; Sigel, H. Acid-Base and Metal Ion-Binding Properties of 9-[2-(2-Phosphonoethoxy)ethyl]adenine (PEEA), a Relative of the Antiviral Nucleotide Analogue 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA). An Exercise on the Quantification of Isomeric Complex Equilibria in Solution. Inorg. Chem. 2005, 44, 5104–5117. [Google Scholar]
- Fernández-Botello, A.; Operschall, B.P.; Holý, A.; Moreno, V.; Sigel, H. Metal Ion-Binding Properties of 9-[2-(Phosphonomethoxy)ethyl]-2-aminopurine (PME2AP), an Isomer of the Antiviral Nucleotide Analogue 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA). Steric Guiding of Metal Ion-Coordination by the Purine-Amino Group. Dalton Trans. 2010, 39, 6344–6354. [Google Scholar] [CrossRef]
- Sigel, H.; Chen, D.; Corfù, N.A.; Gregáň, F.; Holý, A.; Strašák, M. Metal-Ion-Coordinating Properties of Various Phosphonate Derivatives, Including 9-[2-(Phosphonylmethoxy)ethyl]adenine (PMEA)—An Adenosine Monophosphate (AMP) Analogue with Antiviral Properties. Helv. Chim. Acta 1992, 75, 2634–2656. [Google Scholar] [CrossRef]
- Sigel, H. Intramolecular Equilibria in Metal Ion Complexes of Artificial Nucleotide Analogues with Antiviral Properties. A Case Study. Coord. Chem. Rev. 1995, 144, 287–319. [Google Scholar] [CrossRef]
- Sigel, H.; Song, B. Solution Structures of Nucleotide Metal Ion Complexes. Isomeric Equilibria. Met. Ions Biol. Syst. 1996, 32, 135–205. [Google Scholar]
- Sigel, H.; Kapinos, L.E. Quantification of Isomeric Equilibria for Metal Ion Complexes Formed in Solution by Phosphate or Phosphonate Ligands with a Weakly Coordinating Second Site. Coord. Chem. Rev. 2000, 200–202, 563–594. [Google Scholar] [CrossRef]
- Massoud, S.S.; Sigel, H. Metal Ion Coordinating Properties of Pyrimidine-Nucleoside 5′-Monophosphates (CMP, UMP, TMP) and of Simple Phosphate Monoesters, Including D-Ribose 5′-Monophosphate. Establishment of Relations Between Complex Stability and Phosphate Basicity. Inorg. Chem. 1988, 27, 1447–1453. [Google Scholar] [CrossRef]
- Martin, R.B.; Sigel, H. Quantification of Intramolecular Ligand Equilibria in Metal-Ion Complexes. Comments Inorg. Chem. 1988, 6, 285–314. [Google Scholar] [CrossRef]
- Sigel, H.; Massoud, S.S.; Tribolet, R. Comparison of the Metal Ion Coordinating Properties of Tubercidin 5′-Monophosphate (7-Deaza-AMP) with Those of Adenosine 5′-Monophosphate (AMP) and 1,N6-Ethenoadenosine 5′-Monophosphate (ε-AMP). Definite Evidence for Metal Ion-Base Backbinding to N-7 and Extent of Macrochelate Formation in M(AMP) and M(ε-AMP). J. Am. Chem. Soc. 1988, 110, 6857–6865. [Google Scholar]
- Blindauer, C.A. Untersuchungen zu Stabilität, Struktur und Reaktivität von Metallionenkomplexen Einiger Antiviraler Nukleotid-Analoga; Inauguraldissertation. Ph.D. Thesis, Universität Basel, Basel, Switzerland, 1998; pp. 1–235. [Google Scholar]
- Diebler, H. Stability and Structure of Complexes of Transition Metal Ions with Nucleotides and Related Compounds. J. Mol. Catal. 1984, 23, 209–217. [Google Scholar] [CrossRef]
- Sigel, H. Isomeric Equilibria in Complexes of Adenosine 5′-Triphosphate with Divalent Metal Ions. Solution Structures of M(ATP)2− Complexes. Eur. J. Biochem. 1987, 165, 65–72. [Google Scholar] [CrossRef]
- Sigel, H. Metal-Nucleotide Interactions. ACS Symp. Ser. 1989, 402, 159–204. [Google Scholar]
- Sigel, H. Have Adenosine 5′-Triphosphate (ATP4−) and Related Purine-Nucleotides Played a Role in Early Evolution? ATP, Its Own ‘Enzyme’ in Metal Ion Facilitated Hydrolysis! Inorg. Chim. Acta 1992, 198, 1–11. [Google Scholar] [CrossRef]
- Sigel, H. Interactions of Metal Ions with Nucleotides and Nucleic Acids and Their Constituents. Chem. Soc. Rev. 1993, 22, 255–267. [Google Scholar] [CrossRef]
- Holý, A.; Günter, J.; Dvořákova, H.; Masojídkova, M.; Andrei, G.; Snoeck, R.; Balzarini, J.; De Clercq, E. Structure−Antiviral Activity Relationship in the Series of Pyrimidine and Purine N-[2-(2-Phosphonomethoxy)ethyl] Nucleotide Analogues. 1. Derivatives Substituted at the Carbon Atoms of the Base. J. Med. Chem. 1999, 42, 2064–2086. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Botello, A.; Holý, A.; Moreno, V.; Operschall, B.P.; Sigel, H. Intramolecular π-π Stacking Interactions in Aqueous Solution in Mixed-Ligand Copper(II) Complexes Formed by Heteroaromatic Amines and the Nucleotide Analogue 9-[2-(Phos phonomethoxy)ethyl]-2-aminopurine (PME2AP), an Isomer of the Antivirally Active 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA). (Ternary Complexes in Solution. Part 69). Inorg. Chim. Acta 2009, 362, 799–810. [Google Scholar]
- De Clercq, E. The Holý Trinity: The Acyclic Nucleoside Phosphonates. Adv. Pharmacol. 2013, 67, 293–316. [Google Scholar]
- Holý, A. Phosphonomethoxyalkyl Analogs of Nucleotides. Curr. Pharm. Des. 2003, 9, 2567–2592. [Google Scholar] [CrossRef]
- Gómez-Coca, R.B.; Sigel, A.; Operschall, B.P.; Holý, A.; Sigel, H. Solution Properties of Metal Ion Complexes Formed with the Antiviral and Cytostatic Nucleotide Analogue 9-[2-(Phosphonomethoxy)ethyl]-2-amino-6-dimethylaminopurine (PME2A6DMAP). Can. J. Chem. 2014, 92, 771–780. [Google Scholar] [CrossRef]
- Blindauer, C.A.; Sjåstad, T.I.; Holý, A.; Sletten, E.; Sigel, H. Aspects of the Co-ordination Chemistry of the Antiviral Nucleotide Analogue, 9-[2-(Phosphonomethoxy)ethyl]-2,6-diaminopurine (PMEDAP). J. Chem. Soc., Dalton Trans. 1999, 3661–3671. [Google Scholar] [CrossRef]
- Blindauer, C.A.; Holý, A.; Sigel, H. Metal Ion-Binding Properties of the Nucleotide Analogue 1-[2-(Phosphonomethoxy)ethyl]cytosine (PMEC) in Aqueous Solution. Coll. Czech. Chem. Commun. 1999, 64, 613–632. [Google Scholar] [CrossRef]
- Sigel, H. On the Metal Ion-Coordinating Properties of the Antiviral Nucleotide Analogue 9-[2-(Phosphonomethoxy)ethyl]adenine and Related Compounds. J. Indian Chem. Soc. 1997, 74, 261–271. [Google Scholar] [CrossRef]
- Blindauer, C.A.; Emwas, A.H.; Holý, A.; Dvořákova, H.; Sletten, E.; Sigel, H. Complex Formation of the Antiviral 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA) and of Its N1, N3, and N7 Deaza Derivatives with Copper(II) in Aqueous Solution. Chem. Eur. J. 1997, 3, 1526–1536. [Google Scholar] [CrossRef]
- Gómez-Coca, R.B.; Kapinos, L.E.; Holý, A.; Vilaplana, R.A.; González-Vílchez, F.; Sigel, H. Metal Ion-Binding Properties of 9-(4-Phosphonobutyl)adenine (dPMEA), a Sister Compound of the Antiviral Nucleotide Analogue 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA), and Quantification of the Equilibria Involving Four Cu(PMEA) Isomers. J. Chem. Soc. Dalton Trans. 2000, 13, 2077–2084. [Google Scholar] [CrossRef]
- Holý, A.; Votruba, I.; Merta, A.; Černý, J.; Veselý, J.; Vlach, J.; Šedivá, K.; Rosenberg, I.; Otmar, M.; Hřebabecký, H.; et al. Acyclic Nucleotide Analogues: Synthesis, Antiviral Activity and Inhibitory Effects on some Cellular and Virus-Encoded Enzymes in vitro. Antivir. Res. 1990, 13, 295–311. [Google Scholar] [CrossRef]
- Neyts, J.; Stals, F.; Bruggeman, C.; De Clercq, E. Activity of the Anti-HIV Agent 9-(2-phosphonyl-methoxyethyl)-2,6-diaminopurine against Cytomegalovirus in vitro and in vivo. Eur. J. Clin. Microbiol. Infect. Dis. 1993, 12, 437–446. [Google Scholar] [CrossRef]
- Franek, F.; Holý, A.; Votruba, I.; Eckschlager, T. Acyclic Nucleotide Analogues Suppress Growth and Induce Apoptosis in Human Leukemia Cell Lines. Int. J. Oncol. 1999, 14, 745–797. [Google Scholar] [CrossRef]
- Kramata, P.; Votruba, I.; Otová, B.; Holý, A. Different Inhibitory Potencies of Acyclic Phosphonomethoxyalkyl Nucleotide Analogs toward DNA Polymerases alpha, delta and epsilon. Mol. Pharmacol. 1996, 49, 1005–1011. [Google Scholar]
- Valeriánová, M.; Otová, B.; Bílá, V.; Hanzalová, J.; Votruba, I.; Holý, A.; Eckschlager, T.; Krejčí, O.; Trka, J. PMEDAP and Its N6-Substituted Derivatives: Genotoxic Effect and Apoptosis in in vitro Conditions. J. Anticancer Res. 2003, 23, 4933–4939. [Google Scholar]
- Gómez-Coca, R.B.; Blindauer, C.A.; Sigel, A.; Operschall, B.P.; Holý, A.; Sigel, H. Extent of Intramolecular π-Stacks in Aqueous Solution in Mixed-Ligand Copper(II) Complexes Formed by Heteroaromatic Amines and Several 2-Aminopurine Derivatives of the Antivirally Active Nucleotide Analogue 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA). (Ternary Complexes. Part 71). Chem. Biodivers. 2012, 9, 2008–2034. [Google Scholar]
- Amsler, P.E.; Sigel, H. Hydrolysis of Nucleoside Phosphates. V. Comparison of the Metal-Ion-Promoted Dephosphorylation of the 5′-Triphosphates of Adenosine, Inosine, Guanosine and Cytidine by Mn2+, Ni2+ and Zn2+ in Binary and Ternary Complexes. Eur. J. Biochem. 1976, 63, 569–581. [Google Scholar] [CrossRef]
- Sigel, H.; Tribolet, R.; Malini-Balakrishnan, R.; Martin, R.B. Comparison of the Stabilities of Monomeric Metal Ion Complexes Formed with Adenosine 5′-Triphosphate (ATP) and Pyrimidine-Nucleoside 5′-Triphosphates (CTP, UTP, TTP) and Evaluation of the Isomeric Equilibria in the Complexes of ATP and CTP. Inorg. Chem. 1987, 26, 2149–2157. [Google Scholar] [CrossRef]
- Sigel, H.; Sigel, A. (Eds.) Zinc and Its Role in Biology and Nutrition. In Metal Ions in Biological Systems; Marcel Dekker, Inc.: New York, NY, USA, 1983; Volume 15, pp. 1–493. [Google Scholar]
- Sigel, H.; Martin, R.B. The Colourless “Chameleon” or the Peculiar Properties of Zn2+ in Complexes in Solution. Quantification of Equilibria Involving a Change of the Coordination Number of the Metal Ion. Chem. Soc. Rev. 1994, 23, 83–91. [Google Scholar] [CrossRef]
- Sun, G.; Budde, R.J. Requirement for an Additional Divalent Metal Cation to Activate Protein Tyrosine Kinases. Biochemistry 1997, 36, 2139–2146. [Google Scholar] [CrossRef]
- Knape, M.J.; Ballez, M.; Berghardt, N.C.; Zimmermann, B.; Bertinetti, D.; Kornev, A.P.; Herberg, F.W. Divalent Metal Ions Control Activity and Inhibition of Protein Kinases. Metallomics 2017, 9, 1576–1584. [Google Scholar] [CrossRef]
- Jacobsen, D.M.; Bao, Z.-Q.; O’Brien, P.; Brooks, C.L., 3rd; Young, M.A. Price to be Paid for Two-Metal Catalysis. Magnesium Ions that Accelerate Chemistry Unavoidably Limit Product Release from a Protein Kinase. J. Am. Chem. Soc. 2012, 134, 15357–15370. [Google Scholar] [CrossRef]
- Sigel, H. Metal Ion-Assisted Stacking Interactions and the Facilitated Hydrolysis of Nucleoside 5′-Triphosphates. Pure Appl. Chem. 1998, 70, 969–976. [Google Scholar] [CrossRef]
- Job, M.P. Sur la Constitution des Solutions Chlorhydriques de Sels de Cobalt. C. R. Hebd. Séances Acad. Sci. 1933, 196, 181–183. [Google Scholar]
- Slater, J.P.; Mildvan, A.S.; Loeb, L.A. Zinc in DNA Polymerases. Biochem. Biophys. Res. Commun. 1971, 44, 37–43. [Google Scholar] [CrossRef]
- Palermo, G.; Cavalli, A.; Klein, M.L.; Alfonso-Prieto, M.; Dal Peraro, M.; De Vivo, M. Catalytic Metal Ions and Enzymatic Progressing of DNA and RNA. Accounts Chem. Res. 2015, 48, 220–228. [Google Scholar] [CrossRef]
- Wu, F.Y.-H.; Wu, C.-W. The Role of Zinc in DNA and RNA Polymerases. Met. Ions Biol. Syst. 1983, 15, 157–192. [Google Scholar]
- Scrutton, M.C.; Wu, C.W.; Goldthwait, D.A. The Presence and Possible Role of Zinc in RNA Polymerase Obtained from Escherichia coli. Proc. Natl. Acad. Sci. USA 1971, 68, 2497–2501. [Google Scholar] [CrossRef] [Green Version]
- Eichhorn, G.L. The Function of Metal Ions in Genetic Regulation. Met. Ions Biol. Syst. 1980, 10, 1–21. [Google Scholar]
- Genna, V.; Donati, E.; De Vivo, M. The Catalytic Mechanism of DNA and RNA Polymerases. ACS Catalysis 2018, 8, 11103–11118. [Google Scholar] [CrossRef]
- Broom, A.D.; Schweizer, M.P.; Ts’o, P.O.P. Interaction and Association of Bases and Nucleosides in Aqueous Solutions. V. Studies of the Association of Purine Nucleosides by Vapor Pressure Osmometry and by Proton Magnetic Resonance. J. Am. Chem. Soc. 1967, 89, 3612–3622. [Google Scholar] [CrossRef]
- Scheller, K.H.; Hofstetter, F.; Mitchell, P.R.; Prijs, B.; Sigel, H. Macrochelate Formation in Monomeric Metal Ion Complexes of Nucleoside 5′-Triphosphates and the Promotion of Stacking by Metal Ions. Comparison of the Self-Association of Purine and Pyrimidine 5′-Triphosphates Using Proton Nuclear Magnetic Resonance. J. Am. Chem. Soc. 1981, 103, 247–260. [Google Scholar] [CrossRef]
- Mitchell, P.R.; Sigel, H. A Proton Nuclear Magnetic Resonance Study of Self-Stacking in Purine and Pyrimidine Nucleosides and Nucleotides. Eur. J. Biochem. 1978, 88, 149–154. [Google Scholar] [CrossRef] [PubMed]
- Tribolet, R.; Sigel, H. Influence of the Protonation Degree on the Self-Association Properties of Adenosine 5′-Triphosphate (ATP). Eur. J. Biochem. 1988, 170, 617–626. [Google Scholar] [CrossRef] [PubMed]
- Corfù, N.A.; Tribolet, R.; Sigel, H. Comparison of the Self-Association Properties of the 5′-Triphosphates of Inosine (ITP), Guanosine (GTP), and Adenosine (ATP). Further Evidence for Ionic Interactions in the Highly Stable Dimeric [H2(ATP) Stack. Eur. J. Biochem. 1990, 191, 721–735. [Google Scholar] [CrossRef]
- Scheller, K.H.; Sigel, H. A Proton Nuclear Magnetic Resonance Study of Purine and Pyrimidine Nucleoside 5′-Diphosphates. Extent of Macrochelate Formation in Monomeric Metal Ion Complexes and Promotion of Self-Stacking by Metal Ions. J. Am. Chem. Soc. 1983, 105, 5891–5900. [Google Scholar] [CrossRef]
- Sigel, H.; Blindauer, C.A.; Holý, A.; Dvořáková, H. Facilitation of the Copper(II)-Promoted Dephosphorylation of Adenosine 5′-Triphosphate (ATP4−) by the Antiviral Nucleotide Analogue, 9-[2-(Phosphonomethoxy)ethyl]adenine (PMEA). Chem. Commun. 1998, 1219–1220. [Google Scholar] [CrossRef]
- Sigel, H.; Scheller, K.H. On the Metal-Ion Coordinating Properties of the 5′-Monophosphates of 1,N6-Ethenoadenosine (ε-AMP), Adenosine, and Uridine. Comparison of the Macrochelate Formation in the Complexes of ε-AMP, AMP, ADP, and ATP. Eur. J. Biochem. 1984, 138, 291–299. [Google Scholar] [CrossRef]
- Sigel, H. Self-Association, Protonation, and Metal-Coordination of 1,N6-Ethenoadenine Derivatives in Comparison with Their Parent Compounds Adenosine, AMP and ATP. Chimia 1987, 41, 11–26. [Google Scholar] [CrossRef]
- Sigel, H.; Brintzinger, H. Adenosin-5′-monophosphat-N(1)-oxid. Ein ‘Ambivalentes’ Ligandsystem. Helv. Chim. Acta 1964, 47, 1701–1717. [Google Scholar] [CrossRef]
- Sigel, H.; Prijs, B. Ternäre Komplexe in Lösung. IV. Einfluss von 2,2’-Bipyridyl auf Stabilität und Acidität des Cu2+-Adenosin-5′-monophosphat-N(1)-oxid-1:1-Komplexes. Helv. Chim. Acta 1967, 50, 2357–2362. [Google Scholar] [CrossRef] [PubMed]
- Sigel, H. The Ambivalent Properties of Some Base-Modified Nucleotides. Met. Ions Biol. Syst. 1979, 8, 125–158. [Google Scholar]
- Sigel, H.; Naumann, C.F. Ternary Complexes in Solution. XXIV. Metal Ion Bridging of Stacked Purine-Indole Adducts. The Mixed-Ligand Complexes of Adenosine 5′-Triphosphate, Tryptophan, and Manganese(II), Copper(II), or Zinc(II). J. Am. Chem. Soc. 1976, 98, 730–739. [Google Scholar] [CrossRef]
- Mitchell, P.R.; Prijs, B.; Sigel, H. On the Position of the Intramolecular Equilibrium between Opened and Aromatic-Ring Stacked Forms in Ternary Complexes Composed of Adenosine 5′-Triphosphate, Mg2+ or Zn2+, and L-Tryptophanate, and in Related Ternary Systems. (Part 32). Helv. Chim. Acta 1979, 62, 1723–1735. [Google Scholar] [CrossRef]
- Sigel, H. Stability, Structure and Reactivity of Mixed Ligand Complexes in Solution. In Coordination Chemistry—20; Banerjea, D., Ed.; IUPAC through Pergamon Press: Oxford, UK; New York, NY, USA, 1980; pp. 27–45. [Google Scholar]
- Sigel, H.; Fischer, B.E.; Farkas, E. Metal Ion-Promoted Hydrophobic Interactions between Nucleotides and Amino Acids. Mixed-Ligand Adenosine 5′-Triphosphate/Metal Ion(II)/L-Leucinate Systems and Related Ternary Complexes. (Part 42). Inorg. Chem. 1983, 22, 925–934. [Google Scholar] [CrossRef]
- Naumann, C.F.; Sigel, H. Ternary Complexes in Solution. XVIII. The Stability-Enhancement of Nucleotide-Containing Charge-Transfer Adducts through the Formation of a Metal Ion Bridge. J. Am. Chem. Soc. 1974, 96, 2750–2756. [Google Scholar] [CrossRef]
- Chaudhuri, P.; Sigel, H. Ternary Complexes in Solution. 26. Stacking Interactions in the Mixed-Ligand Complexes Formed by Adenosine or Inosine 5′-Triphosphate, 2,2’-Bipyridyl, and Cobalt(II), Nickel(II), Copper(II), or Zinc(II). Evidence for Phosphate-Protonated Complexes. J. Am. Chem. Soc. 1977, 99, 3142–3150. [Google Scholar] [CrossRef]
- Mitchell, P.R.; Sigel, H. Enhanced Stability of Ternary Metal Ion/Adenosine 5′-Triphosphate Complexes. Cooperative Effects Caused by Stacking Interactions in Complexes Containing Adenosine Triphosphate, Phenanthroline, and Magnesium, Calcium, or Zinc Ions. (Ternary Complexes in Solution. Part 28). J. Am. Chem. Soc. 1978, 100, 1564–1570. [Google Scholar]
- Orioli, P.; Cini, R.; Donati, D.; Mangani, S. Crystal and Molecular Structure of the Ternary Complex Bis[(adenosine 5′-triphosphato)(2,2’-bipyridine)zinc(II)] Tetrahydrate. J. Am. Chem. Soc. 1981, 103, 4446–4452. [Google Scholar] [CrossRef]
- Sheldrick, W.S. Preparation and Structures of Ternary Copper(II) Complexes of ADP and ATP Models for Enzyme-Metal Ion-Nucleoside Polyphosphate Complexes. Z. Naturforsch. B Anorg. Chem. Org. Chem. 1982, 37, 863–871. [Google Scholar] [CrossRef]
- Buisson, D.H.; Sigel, H. Protection of Adenosine 5′-Triphosphate toward Hydrolysis by the Formation of a Mixed-Ligand Metal Ion Complex. Angew. Chem. Internat. Ed. Engl. 1972, 11, 1025. [Google Scholar] [CrossRef] [PubMed]
- Sigel, H.; Corfù, N.A. Facilitated Formation of High-Molecular-Weight Associates of Adenosine 5′-Triphosphate (ATP). Naturwissenschaften 1995, 82, 237–238. [Google Scholar] [CrossRef] [PubMed]
- Sigel, H.; Corfù, N.A. The Assisted Self-Association of ATP4− by a Poly(amino acid), [poly(Lys)], and Its Significance for Cell Organelles that Contain High Concentrations of Nucleotides. Eur. J. Biochem. 1996, 240, 508–517. [Google Scholar] [CrossRef] [PubMed]
- Pletscher, A.; Da Prada, M.; Berneis, K.H.; Steffen, H.; Lütold, B.; Weder, H.G. Molecular Organization of Amine Storage Organelles of Blood Platelets and Adrenal Medulla. Adv. Cytopharmacol. 1974, 2, 257–264. [Google Scholar]
- Da Prada, M.; Richards, J.G.; Kettler, R. Amine Storage Organelles in Platelets. In Platelets in Biology and Pathology-2; Gordon, J.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1981; pp. 107–145. [Google Scholar]
- Berneis, K.H.; Da Prada, M.; Pletscher, A. Metal-Dependent Aggregation of Nucleotides with Formation of Biphasic Liquid Systems. Biochim. Biophys. Acta 1970, 215, 547–549. [Google Scholar] [CrossRef]
- Da Prada, M.; Berneis, K.H.; Pletscher, A. Storage of Catecholamines in Adrenal Medulary Granules: Formation of Aggregates with Nucleotides. Life Sci. 1971, 10, 639–646. [Google Scholar] [CrossRef]
- Berneis, K.H.; Goetz, U.; Da Prada, M.; Pletscher, A. Interaction of Aggregated Catecholamines and Nucleotides with Intragranular Proteins. Naunyn-Schmiedeberg’s Arch. Pharmacol. 1973, 277, 291–296. [Google Scholar] [CrossRef]
- Winkler, H.; Carmichael, S.W. The Chromaffin Granule. In The Secretory Granule; Poisner, A.M., Trifaró, J.M., Eds.; Elsevier Biomedical Press: Amsterdam, The Netherlands; New York, NY, USA; Oxford, UK, 1982; pp. 3–79. [Google Scholar]
- Winkler, H.; Apps, D.K.; Fischer-Colbrie, R. The Molecular Function of Adrenal Chromaffin Granules: Established Facts and Unresolved Topics. Neuroscience 1986, 18, 261–290. [Google Scholar] [CrossRef]
- Dzhandzhugazyan, K.; Bock, E. Demonstration of an Extracellular ATP-Binding Site in NCAM: Functional Implications of Nucleotide Binding. Biochemistry 1997, 36, 15381–15395. [Google Scholar] [CrossRef]
- Kelley, S.O.; Holmlin, R.E.; Stemp, E.D.A.; Barton, J.K. Photoinduced Electron Transfer in Ethidium-Modified DNA Duplexes: Dependence on Distance and Base Stacking. J. Am. Chem. Soc. 1997, 119, 9861–9870. [Google Scholar] [CrossRef]
- Giese, B. Electron Transfer in DNA. Curr. Opin. Chem. Biol. 2002, 6, 612–618. [Google Scholar] [CrossRef]
- Naumann, C.F.; Prijs, B.; Sigel, H. Adenosine and Inosine 5′-Triphosphates: Protonation, Metal Ion Coordination, and Charge-Transfer Interaction between Two Ligands within Ternary Complexes. Eur. J. Biochem. 1974, 41, 209–216. [Google Scholar] [CrossRef] [PubMed]
- Sigel, H.; Becker, K.; McCormick, D.B. Ternary Complexes in Solution. III. Influence of 2,2’-Bipyridyl on the Stability of 1:1 Complexes of Co2+, Ni2+, Cu2+, and Zn2+ with Hydrogen Phosphate, Adenosine 5′-Monophosphate, and Adenosine 5′-Triphosphate. Biochim. Biophys. Acta 1967, 148, 655–664. [Google Scholar] [CrossRef]
- Sigel, H. Hydrophobic Interactions in Biological Systems: Some Background Information Based on Ligand-Ligand Interactions in Metal Ion Complexes. Pure Appl. Chem. 1989, 61, 923–932. [Google Scholar] [CrossRef]
- Massoud, S.S.; Tribolet, R.; Sigel, H. Metal-Ion-Governed Molecular Recognition: Extent of Intramolecular Stack Formation in Mixed-Ligand Copper(II) Complexes Containing a Heteroaromatic N Base and an Adenosine Monophosphate (2’-AMP, 3′-AMP, or 5′-AMP). A Structuring Effect of the Metal-Ion Bridge. Eur. J. Biochem. 1990, 187, 387–393. [Google Scholar]
- Yamauchi, O.; Odani, A.; Masuda, H.; Sigel, H. Stacking Interactions Involving Nucleotides and Metal Ion Complexes. Met. Ions Biol. Syst. 1996, 32, 207–270. [Google Scholar] [CrossRef]
- Tribolet, R.; Malini-Balakrishnan, R.; Sigel, H. Influence of Decreasing Solvent-Polarity (Dioxane-Water Mixtures) on the Stability and Structure of Binary and Ternary Complexes of Adenosine 5′-Triphosphate and Uridine 5′-Triphosphate. J. Chem. Soc. Dalton Trans. 1985, 2291–2303. [Google Scholar] [CrossRef]
- Fischer, B.E.; Sigel, H. Ternary Complexes in Solution. 35. Intramolecular Hydrophobic Ligand-Ligand Interactions in Mixed Ligand Complexes Containing an Aliphatic Amino Acid. J. Am. Chem. Soc. 1980, 102, 2998–3008. [Google Scholar] [CrossRef]
- Sigel, H.; Malini-Balakrishnan, R.; Häring, U.K. Ternary Complexes in Solution (Part 48). Influence of Organic Solvents on Intramolecular Aromatic-Ring Stacks in Aqueous Mixed-Ligand Metal Ion Complexes. Opposing Solvent Effects. J. Am. Chem. Soc. 1985, 107, 5137–5148. [Google Scholar] [CrossRef]
- Bianchi, E.M.; Sajadi, S.A.A.; Song, B.; Sigel, H. Intramolecular Stacking Interactions in Mixed Ligand Complexes Formed by Copper(II), 2,2’-Bipyridine or 1,10-Phenanthroline, and Monoprotonated or Deprotonated Adenosine 5′-Diphosphate (ADP3−). Evaluation of Isomeric Equilibria. Inorg. Chim. Acta 2000, 300–302, 487–498. [Google Scholar] [CrossRef]
- Aoki, K. X-Ray Evidence for the Metal Ion Bridged Intra- and Intermolecular Stacking Interactions between Nucleotide Bases and Aromatic Heterocyclic Rings within the Ternary Complex [Cu(5′-AMP)(bpy)(H2O)]2.(NO3)2.6H2O. J. Am. Chem. Soc. 1978, 100, 7106–7108. [Google Scholar] [CrossRef]
- Naumann, C.F.; Sigel, H. Ternary Complexes in Solution. (Part 21). Bridging of the Stacked Adduct Between Tryptophan and Adenosine 5′-Triphosphate by Zinc(II). FEBS Lett. 1974, 47, 122–124. [Google Scholar] [CrossRef] [Green Version]
- Orenberg, J.B.; Fischer, B.E.; Sigel, H. Binary and Ternary Complexes of Metal Ions, Nucleoside 5′-Monophosphates, and Amino Acids. (Ternary Complexes in Solution. Part 33). J. Inorg. Nucl. Chem. 1980, 42, 785–792. [Google Scholar] [CrossRef]
- Sigel, H.; Scheller, K.H.; Scheller-Krattiger, V.; Prijs, B. Comparison of the Properties of Binary and Ternary Metal Ion Complexes of 1,N6-Ethenoadenosine 5′-Triphosphate (ε-ATP) and Adenosine 5′-Triphosphate (ATP), Including Macrochelate and Purine-Indole Stack Formation. J. Am. Chem. Soc. 1986, 108, 4171–4178. [Google Scholar] [CrossRef]
- Toulmé, J.-J. Stacking Interactions between Aromatic Amino Acids and the Adenine Ring of ATP in Zinc-Mediated Ternary Complexes. Bioinorg. Chem. 1978, 8, 319–329. [Google Scholar] [CrossRef]
- Basosi, R.; Gaggelli, E.; Tiezzi, E. Electron Spin Resonance Evidence of Ternary Complex Formation. J. Chem. Res. (S) 1977, 278–279. [Google Scholar]
- Basosi, R.; Gaggelli, E.; Tiezzi, E. Mixed Ligand Complexes in Solution of Manganous Ion. J. Chem. Soc. Faraday Trans. 1 1979, 75, 2433–2438. [Google Scholar] [CrossRef]
- Gaggelli, E.; Rossi, C.; Tiezzi, E. Noncovalent Interactions and Paramagnetic Relaxation Probes. Investigation of the Correlation Times. J. Phys. Chem. 1980, 84, 116–118. [Google Scholar] [CrossRef]
- Arena, G.; Cali, R.; Cucinotta, V.; Musumeci, S.; Rizzarelli, E.; Sammartano, S. Thermodynamics of Metal Complexes with Ligand–Ligand Interaction. Mixed Complexes of Copper(II) and Zinc(II) with Adenosine 5′-Triphosphate and L-Histidine or Histamine. J. Chem. Soc. Dalton Trans. 1984, 1651–1658. [Google Scholar] [CrossRef]
- Sigel, H.; Tribolet, R.; Yamauchi, O. The Imidazole Group and Its Stacking Properties in Mixed Ligand Metal Ion Complexes. Comments Inorg. Chem. 1990, 9, 305–330. [Google Scholar] [CrossRef]
- Chen, D.; Bastian, M.; Gregáň, F.; Holý, A.; Sigel, H. Ternary Complexes in Solution (Part 55) with Phosphonates as Ligands. Various Intramolecular Equilibria in Mixed-Ligand Complexes Containing the Antiviral 9-(2-Phosphonomethoxyethyl)adenine, an Adenosine Monophosphate Analogue. J. Chem. Soc. Dalton Trans. 1993, 1537–1546. [Google Scholar] [CrossRef]
- Rees, D.C. Experimental Evaluation of the Effective Dielectric Constant of Proteins. J. Mol. Biol. 1980, 141, 323–326. [Google Scholar] [CrossRef]
- Moore, G.R. Control of Redox Properties of Cytochrome c by Special Electrostatic Interactions. FEBS Lett. 1983, 161, 171–175. [Google Scholar] [CrossRef] [Green Version]
- Rogers, N.K.; Moore, G.R.; Sternberg, M.J.E. Electrostatic Interactions in Globular Proteins: Calculations of the pH Dependence of the Redox Potential of Cytochrome c551. J. Mol. Biol. 1985, 182, 613–616. [Google Scholar] [CrossRef]
- Sigel, H.; Martin, R.B.; Tribolet, R.; Häring, U.K.; Malini-Balakrishnan, R. An Estimation of the Equivalent Solution Dielectric Constant in the Active-Site Cavity of Metalloenzymes. Dependence of Carboxylate–Metal-Ion Complex Stabilities on the Polarity of Mixed Aqueous/Organic Solvents. Eur. J. Biochem. 1985, 152, 187–193, See also the comment in the footnote on page 258 in: Bastian, M.; Sigel, H. On the Metal Ion Binding Properties of Orotidine. Inorg. Chim. Acta 1990, 178, 249–259. [Google Scholar] [CrossRef]
- De Meis, L. Role of Water in the Energy of Hydrolysis of Phosphate Compounds—Energy Transduction in Biological Membranes. Biochim. Biophys. Acta 1989, 973, 333–349. [Google Scholar] [CrossRef]
- Åkerlöf, G.; Short, O. The Dielectric Constant of Dioxane-Water Mixtures between 0 and 80. J. Am. Chem. Soc. 1936, 58, 1241–1243, Correction in. J. Am. Chem. Soc. 1953, 75, 6357. [Google Scholar] [CrossRef]
- Critchfield, F.E.; Gibson, J.A., Jr.; Hall, J.L. Dielectric Constant for the Dioxane-Water System from 20 to 35°. J. Am. Chem. Soc. 1953, 75, 1991–1992. [Google Scholar] [CrossRef]
- Chen, D.; Gregáň, F.; Holy, A.; Sigel, H. Solvent-Dependent Metal Ion-Adenine Recognition. Quantification of the Intramolecular Equilibria between Various Isomers of the Cu2+ Complexes Formed in Water-Dioxane Mixtures with the Anions of the Antiviral 9-(2-(Phosphonomethoxy)ethyl)adenine (PMEA), an Adenosine Monophosphate (AMP) Analogue. Inorg. Chem. 1993, 32, 5377–5384. [Google Scholar]
- Magalhães, M.C.F.; Sigel, H. Establishment of Relations between Complex Stability and Phosphate Group Basicity for the Copper(II) Complexes of Simple Phosphate Monoesters in Dioxane-Water Mixtures. J. Indian Chem. Soc. 1992, 69, 437–441. [Google Scholar]
- Bastian, M.; Sigel, H. Stability and Structure of the Mg2+, Ca2+ and Cu2+ Complexes of Orotidinate 5′-Monophosphate (OMP)3− in Various Aqueous 1,4-Dioxane Mixtures. Inorg. Chim. Acta 1991, 187, 227–237. [Google Scholar] [CrossRef]
- Liang, G.; Sigel, H. Solvent-Dependent Metal Ion-Nucleic Base Recognition. Extent of Macrochelate Formation in the Binary Copper(II) Complexes of Adenosine 5′-Monophosphate (AMP) and Adenosine 5′-Triphosphate (ATP) in Water-Dioxane Mixtures. Inorg. Chem. 1990, 29, 3631–3632. [Google Scholar] [CrossRef]
- Bianchi, E.M.; Sajadi, S.A.A.; Song, B.; Sigel, H. Stabilities and Isomeric Equilibria in Aqueous Solution of Monomeric Metal Ion Complexes of Adenosine 5′-Diphosphate (ADP3−) in Comparison with Those of Adenosine 5′-Monophosphate (AMP2−). Chem. Eur. J. 2003, 9, 881–892. [Google Scholar] [CrossRef]
- Da Costa, C.P.; Song, B.; Gregáň, F.; Sigel, H. Intramolecular Chelate Formation Involving the Carbonyl Oxygen of Acetyl Phosphate or Acetonylphosphonate in Mixed Ligand Copper(II) Complexes Containing also 2,2’-Bipyridine or 1,10-Phenanthroline. A Decreased Solvent Polarity Favours Metal Ion-Carbonyl Oxygen Recognition. (Part 64). J. Chem. Soc. Dalton Trans. 2000, 6, 899–904. [Google Scholar]
- Rawn, J.D. Biochemistry; Patterson: Burlington, NC, USA, 1989. [Google Scholar]
- Stryer, L. Biochemistry, 4th ed.; Freeman: New York, NY, USA, 1997. [Google Scholar]
- Sigel, H.; Martin, R.B. Coordinating Properties of the Amide Bond. Stability and Structure of Metal Ion Complexes of Peptides and Related Ligands. Chem. Rev. 1982, 82, 385–426. [Google Scholar] [CrossRef]
- Furler, M.; Knobloch, B.; Sigel, R.K.O. Influence of decreased solvent permittivity on the structure and magnesium(II)-binding properties of the catalytic domain 5 of a group II intron ribozyme. Inorg. Chim. Acta 2009, 362, 771–776. [Google Scholar] [CrossRef] [Green Version]
- DasGupta, S. Molecular Crowding and RNA Catalysis. Org. Biomol. Chem. 2020, 18, 7724–7739. [Google Scholar] [CrossRef]
- Fiorini, E.; Paudel, B.; Börner, R.; Sigel, R.K.O.; Rueda, D. Optimal Molecular Crowding Accelerates Group II Intron Folding and Maximizes Catalysis. Proc. Natl. Acad. Sci. USA 2018, 115, 11917–11922. [Google Scholar]
- Irving, H.; Williams, R.J.P. Order of Stability of Metal Complexes. Nature 1948, 162, 746–747. [Google Scholar] [CrossRef]
- Irving, H.; Williams, R.J.P. The Stability of Transition-Metal Complexes. J. Chem. Soc. 1953, 3192–3210. [Google Scholar] [CrossRef]
- Sigel, R.K.O.; Sigel, H. Metal Ion Interactions with Nucleic Acids and Their Constituents. In Bioinorganic Fundamentals and Applications: Metals in Natural Living Systems and Metals in Toxicology and Medicine; Pecoraro, V.L., Hambley, T., Eds.; In Comprehensive Inorganic Chemistry II; Reedijk, J., Poeppelmeier, K., Eds.; Elsevier: Oxford, UK, 2013; Volume 3, pp. 623–660. [Google Scholar]
- Sajadi, S.A.A.; Song, B.; Gregáň, F.; Sigel, H. Acid-Base and Metal Ions-Coordinating Properties of Pyrimidine-Nucleoside 5′-Diphosphates (CDP, UDP, dTDP) and of Several Simple Diphosphate Monoesters. Establishment of Relations between Complex Stability and Diphosphate Basicity. Inorg. Chem. 1999, 38, 439–448. [Google Scholar] [CrossRef] [PubMed]
- Sigel, A.; Operschall, B.P.; Sigel, H. Complex Formation of Lead(II) with Nucleotides and Their Constituents. Met. Ions Life Sci. 2017, 17, 319–402. [Google Scholar]
- Liu, Y.; Wilson, T.J.; Lilley, D.M.J. The Structure of a Nucleolytic Ribozyme that Employs a Catalytic Metal Ion. Nature Chem. Biol. 2017, 13, 508–513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roychowdhury-Saha, M.; Burke, D.H. Extraordinary Rates of Transition Metal Ion-Mediated Ribozyme Catalysis. RNA 2006, 12, 1846–1852. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boots, J.L.; Canny, M.D.; Azimi, E.; Pardi, A. Metal Ion Specificities for Folding and Cleavage Activity in the Schistosoma Hammerhead Ribozyme. RNA 2008, 14, 2212–2222. [Google Scholar] [CrossRef] [Green Version]
- Schnabl, J.; Sigel, R.K.O. Controlling Ribozyme Activity by Metal Ions. Curr. Opin. Chem. Biol. 2010, 14, 269–275. [Google Scholar] [CrossRef] [Green Version]
- Klawuhn, K.; Jansen, J.A.; Souchek, J.; Soukup, G.A.; Soukup, J.K. Analysis of Metal Ion-Dependence in glmS Ribozyme Self-Cleavage and Coenzyme Binding. ChemBioChem 2010, 11, 2567–2571. [Google Scholar] [CrossRef]
- Erat, M.C.; Sigel, R.K.O. Divalent Metal Ions Tune the Self-splicing Reaction of the Yeast Mitochondrial Group II Intron Sc.ai5γ. J. Biol. Inorg. Chem. 2008, 13, 1025–1036. [Google Scholar] [CrossRef] [Green Version]
- Sigel, R.K.O.; Pyle, A.M. Alternative Roles for Metal Ions in Enzyme Catalysis and the Implications for Ribozyme Chemistry. Chem. Rev. 2007, 107, 97–113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sigel, A.; Operschall, B.P.; Griesser, R.; Song, B.; Okruszek, A.; Odani, A.; Katsuta, T.; Lippert, B.; Sigel, H. (N-7)-Platination and Its Effect on (N1)H-Acidification in Nucleoside Phosphate Derivatives. Inorg. Chim. Acta 2016, 452, 137–141. [Google Scholar] [CrossRef]
- Sigel, H.; Sigel, A. The Bio-Relevant Metals of the Periodic Table of the Elements. Zeitschr. für Naturforschung. B 2019, 74b, 461–471. [Google Scholar] [CrossRef]
- Delfosse, V.; Bouchard, P.; Bonneau, E.; Dagenais, P.; Lemay, J.-F.; Lafontaine, D.A.; Legault, P. Riboswitch structure: An internal residue mimicking the purine ligand. Nucleic Acids Res. 2010, 38, 2057–2068. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schnabl, J.; Suter, P.; Sigel, R.K.O. MINAS—A Database of Metal Ions in Nucleic AcidS. Nucleic Acids Res. 2012, 40, D434–D438. [Google Scholar] [CrossRef] [Green Version]
- Kapinos, L.E.; Operschall, B.P.; Larsen, E.; Sigel, H. Understanding the Acid-Base Properties of Adenosine: The Intrinsic Basicities of N1, N3 and N7. Chem. Eur. J. 2011, 17, 8156–8164. [Google Scholar] [CrossRef]
- Saenger, W. Principles of Nucleic Acid Structure; Springer: New York, NY, USA, 1984. [Google Scholar]
- Erat, M.C.; Kovacs, H.; Sigel, R.K.O. Metal Ion-N7 Coordination in a Ribozyme Branch Domain by NMR. J. Inorg. Biochem. 2010, 104, 611–613. [Google Scholar] [CrossRef] [Green Version]
- De Clercq, E.; Holý, A.; Rosenberg, I.; Sakuma, T.; Balzarini, J.; Maudgal, P.C. A Novel Selective Broad-Spectrum Anti-DNA Virus Agent. Nature 1986, 323, 464–467. [Google Scholar] [CrossRef]
- Blindauer, C.A.; Holý, A.; Sigel, A.; Operschall, B.P.; Griesser, R.; Sigel, H. Acid–Base Properties of an Antivirally Active Acyclic Nucleoside Phosphonate: (S)-9-[3-Hydroxy-2-(phosphonomethoxy)propyl]adenine (HPMPA). New J. Chem. 2022, 46, 6484–6493. [Google Scholar] [CrossRef]
- Blindauer, C.A.; Griesser, R.; Holý, A.; Operschall, B.P.; Sigel, A.; Song, B.H.; Sigel, H. Intramolecular π-Stacks in Mixed-Ligand Copper(II) Complexes Formed by Heteroaromatic Amines and Antivirally Active Acyclic Nucleotide Analogues Carrying a Hydroxy-2-(phosphonomethoxy)propyl Residue. J. Coord. Chem. 2018, 71, 1910–1934. [Google Scholar] [CrossRef]
- Blindauer, C.A.; Holý, A.; Operschall, B.P.; Sigel, A.; Song, B.; Sigel, H. Metal Ion-Coordinating Properties in Aqueous Solution of the Antivirally Active Nucleotide Analogue (S)-9-[3-Hydroxy-2-(phosphonomethoxy)propyl]adenine (HPMPA). Quantification of Complex Isomeric Equilibria. Eur. J. Inorg. Chem. 2019, 2019, 3892–3903. [Google Scholar] [CrossRef]
- Blindauer, C.A.; Sigel, A.; Operschall, B.P.; Holý, A.; Sigel, H. Metal-Ion Binding Properties of (S)-1-[3-Hydroxy-2-(phosphonomethoxy)propyl]cytosine (HPMPC, Cidofovir). A Nucleotide Analogue with Activity Against DNA Viruses. Inorg. Chim. Acta 2018, 472, 283–294. [Google Scholar] [CrossRef]
- De Clercq, E. Towards an Effective Chemotherapy of Virus Infections: Therapeutic Potential of Cidofovir [(S)-1-[3-Hydroxy-2-(phosphonomethoxy)propyl]cytosine, HPMPC] for the Treatment of DNA Virus Infections. Collect. Czech. Chem. Commun. 1998, 63, 480–506. [Google Scholar] [CrossRef]
- De Clercq, E.; Li, G. Approved Antiviral Drugs over the Past 50 Years. Clin. Microbiol. Rev. 2016, 29, 695–747. [Google Scholar] [CrossRef] [Green Version]
- Edwards, A.M.; Baric, R.S.; Ollmann Saphire, E.; Ullmer, J.B. Stopping Pandemics before They Start: Lessons Learned from SARS-CoV-2. Science 2022, 375, 1133–1139. [Google Scholar] [CrossRef]
- Klein, D.J.; Moore, P.B.; Steitz, T.A. The Contribution of Metal Ions to the Structural Stability of the Large Ribosomal Subunit. RNA 2004, 10, 1366–1379. [Google Scholar] [CrossRef] [Green Version]
- Erat, M.C.; Sigel, R.K.O. Determination of the Intrinsic Affinities of Multiple Site-Specific Mg2+ Ions Coordinated to Domain 6 of a Group II Intron Ribozyme. Inorg. Chem. 2007, 46, 11224–11234. [Google Scholar] [CrossRef] [Green Version]
- Erat, M.C.; Zerbe, O.; Fox, T.; Sigel, R.K.O. Solution Structure of Domain 6 from a Self-Splicing Group II Intron Ribozyme: A Mg2+ Binding Site is Located Close to the Stacked Branch Adenosine. ChemBioChem 2007, 8, 306–314. [Google Scholar] [CrossRef] [Green Version]
- Sigel, R.K.O.; Vaidya, A.; Pyle, A.M. Metal Ion Binding Sites in a Group II Intron Core. Nat. Struct. Biol. 2000, 7, 1111–1116. [Google Scholar]
- Korth, M.M.T.; Sigel, R.K.O. Unusually High-Affinity Mg2+ Binding at the AU-Rich Sequence within the Antiterminator Hairpin of a Mg2+ Riboswitch. Chem. Biodivers. 2012, 9, 2035–2049. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.W.; Steitz, T.A. The Structural Mechanism of Translocation and Helicase Activity in T7 RNA Polymerase. Cell 2004, 116, 393–404. [Google Scholar] [CrossRef] [Green Version]
- Shan, S.-O.; Yoshida, A.; Sun, S.; Piccirilli, J.A.; Herschlag, D. Three Metal Ions at the Active Site of the Tetrahymena Group I Ribozyme. Proc. Natl. Acad. Sci. USA 1999, 96, 12299–12304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shan, S.-O.; Kravchuk, A.V.; Piccirilli, J.A.; Herschlag, D. Defining the Catalytic Metal Ion Interactions in the Tetrahymena Ribozyme Reaction. Biochemistry 2001, 40, 5161–5171. [Google Scholar] [CrossRef] [PubMed]
- Manigrasso, J.; Chillón, I.; Genna, V.; Vidossich, P.; Somarowthu, S.; Pyle, A.M.; De Vivo, M.; Marcia, M. Visualizing Group II Intron Dynamics between the First and Second Step of Splicing. Nature Commun. 2020, 11, 2837. [Google Scholar] [CrossRef]
- Takeuchi, H.; Murata, H.; Harada, I. Interaction of Adenosine 5′-Triphosphate with Mg2+: Vibrational Study of Coordination Sites by Use of 18O-Labeled Triphosphates. J. Am. Chem. Soc. 1988, 110, 392–397. [Google Scholar] [CrossRef]



















| H2(P) | Ref b | ||
|---|---|---|---|
| CH3OPO(OH)2 | 1.1 ± 0.2 | 6.36 ± 0.01 | [40] |
| CH3PO(OH)2 | 2.10 ± 0.03 | 7.51 ± 0.01 | [41] |
| M2+ | log ΔM(PMEA) | log ΔM(PME) | Δ log Δ | KI/PME | % M(PME)cl |
|---|---|---|---|---|---|
| Mg2+ | 0.16 ± 0.05 | 0.22 ± 0.03 | –0.06 ± 0.06 | 0.66 ± 0.12 | 40 ± 4 |
| Ca2+ | 0.11 ± 0.07 | 0.14 ± 0.05 | –0.03 ± 0.09 | 0.38 ± 0.16 | 28 ± 9 |
| Sr2+ | 0.07 ± 0.05 | 0.07 ± 0.05 | 0.00 ± 0.07 | 0.17 ± 0.14 | 15 ± 10 |
| Ba2+ | 0.08 ± 0.06 | 0.10 ± 0.05 | –0.02 ± 0.08 | 0.26 ± 0.14 | 21 ± 9 |
| Mn2+ | 0.21 ± 0.08 | 0.27 ± 0.05 | –0.06 ± 0.09 | 0.86 ± 0.23 | 46 ± 7 |
| Co2+ | 0.28 ± 0.07 | 0.29 ± 0.06 | –0.01 ± 0.09 | 0.95 ± 0.28 | 49 ± 7 |
| Ni2+ | 0.30 ± 0.07 | 0.19 ± 0.05 | 0.11 ± 0.09 | 0.55 ± 0.19 | 35 ± 8 |
| Cu2+ | 0.77 ± 0.07 | 0.48 ± 0.07 | 0.29 ± 0.10 | 2.02 ± 0.47 | 67 ± 5 |
| Zn2+ | 0.30 ± 0.10 | 0.34 ± 0.06 | –0.04 ± 0.12 | 1.19 ± 0.32 | 54 ± 7 |
| Cd2+ | 0.33 ± 0.05 | 0.30 ± 0.05 | 0.03 ± 0.08 | 1.00 ± 0.25 | 50 ± 6 |
| M2+ | % M(PME2AP)op | % M(PME2AP)cl/O | % M(PME2AP)cl/N7 |
|---|---|---|---|
| Mg2+ | 63 ± 7 | 37 ± 7 | ~0 |
| Ca2+ | 74 ± 14 | 26 ± 14 | ~0 |
| Mn2+ | 59 ± 8 | 41 ± 8 | ~0 |
| Co2+ | 24 ± 4 | 14 ± 6 | 62 ± 7 |
| Ni2+ | 11 ± 2 | 4 ± 3 | 85 ± 4 |
| Cu2+ | 9 ± 2 | 18 ± 6 | 73 ± 6 |
| Zn2+ | 13 ± 3 | 12 ± 5 | 75 ± 6 |
| Cd2+ | 35 ± 7 | 35 ± 11 | 30 ± 13 |
| M2+ | log ΔM(PMEDAP) | log ΔM(PME-R) | Δ log Δ | KI/PMEDAP | %M(PMEDAP)cl/O |
|---|---|---|---|---|---|
| Mg2+ | 0.17 ± 0.05 | 0.16 ± 0.04 | 0.01 ± 0.06 | 0.48 ± 0.17 | 32 ± 8 |
| Ca2+ | 0.12 ± 0.06 | 0.12 ± 0.05 | 0.00 ± 0.08 | 0.32 ± 0.19 | 24 ± 11 |
| Sr2+ | 0.08 ± 0.04 | 0.09 ± 0.05 | –0.01 ± 0.06 | 0.20 ± 0.12 | 17 ± 9 |
| Ba2+ | 0.10 ± 0.06 | 0.11 ± 0.05 | –0.01 ± 0.08 | 0.26 ± 0.19 | 21 ± 12 |
| Mn2+ | 0.18 ± 0.06 | 0.19 ± 0.06 | –0.01 ± 0.08 | 0.51 ± 0.20 | 34 ± 9 |
| Co2+ | 0.33 ± 0.07 | 0.20 ± 0.06 | (0.13 ± 0.09) b | (1.14 ± 0.36)c | (53 ± 8) c |
| Ni2+ | 0.48 ± 0.08 | 0.14 ± 0.07 | (0.34 ± 0.11) b | (2.02 ± 0.54)c | (67 ± 6) c |
| Cu2+ | 0.73 ± 0.07 | 0.48 ± 0.07 | (0.25 ± 0.10) b | (4.37 ± 0.89) c | (81 ± 3) c |
| Zn2+ | 0.40 ± 0.11d | 0.29 ± 0.07 | 0.11 ± 0.13 | 1.51 ± 0.63 | 60 ± 10 d |
| Cd2+ | 0.32 ± 0.13 | 0.30 ± 0.05 | 0.02 ± 0.14 | 1.09 ± 0.63 | 52 ± 14 |
| PE2− = PME2A6DMAP2− | ||||||
|---|---|---|---|---|---|---|
| M2+ | Log ΔM(PE) | log ΔM(PME-R) | Δ log Δ | KI/PE | % M(PE)cl/O | % M(PME-R)cl/O |
| Mg2+ | 0.16 ± 0.04 | 0.16 ± 0.04 | 0.00 ± 0.06 | 0.45 ± 0.13 | 31 ± 6 | 31 ± 6 |
| Ca2+ | 0.10 ± 0.05 | 0.12 ± 0.05 | −0.02 ± 0.07 | 0.26 ± 0.14 | 21 ± 9 | 24 ± 9 |
| Sr2+ | 0.11 ± 0.05 | 0.09 ± 0.05 | 0.02 ± 0.07 | 0.29 ± 0.15 | 22 ± 9 | 19 ± 9 |
| Ba2+ | 0.08 ± 0.06 | 0.11 ± 0.05 | −0.03 ± 0.08 | 0.20 ± 0.17 | 17 ± 11 | 22 ± 9 |
| Mn2+ | 0.19 ± 0.06 | 0.19 ± 0.06 | 0.00 ± 0.08 | 0.55 ± 0.21 | 35 ± 9 | 35 ± 9 |
| Co2+ | 0.21 ± 0.07 | 0.20 ± 0.06 | 0.01 ± 0.09 | 0.62 ± 0.26 | 38 ± 10 | 37 ± 9 |
| Ni2+ | 0.17 ± 0.07 | 0.14 ± 0.07 | 0.03 ± 0.10 | 0.48 ± 0.24 | 32 ± 11 | 28 ± 12 |
| Cu2+ | 0.56 ± 0.07 | 0.48 ± 0.07 | 0.08 ± 0.10 | 2.63 ± 0.59 | 72 ± 4 | 67 ± 5 |
| Zn2+ | 0.28 ± 0.07 | 0.29 ± 0.07 | −0.01 ± 0.10 | 0.91 ± 0.31 | 48 ± 8 | 49 ± 8 |
| Cd2+ | 0.25 ± 0.06 | 0.30 ± 0.05 | −0.05 ± 0.08 | 0.78 ± 0.25 | 44 ± 8 | 50 ± 6 |
| No. | System | K (M−1) |
|---|---|---|
| 1 | Ado | 15 ± 2 |
| 2 | AMP2− | 2.1 ± 0.4 |
| 3 | ADP3− | 1.8 ± 0.5 |
| 4 | ATP4− | 1.3 ± 0.2 |
| 5 | Mg(ATP)2− | 4.0 ± 0.5 |
| 6 | Zn(ATP)2− | ~11.1 ± 4.5 |
| 7 | Cd(ATP)2− | ~17 |
| arm | KI = KI/tot (Equation (29)) | % Cu(arm)(PMEA)int/tot (cf. Equation (29)) | % Cu(arm)(PMEA)op (Equation (24)) | KI/O (Equation (27)) | KI/st (Equations (27) and (29)) c | % Cu(arm)(PMEA)cl/O (Equations (5) and (24)) b | % Cu(arm)(PMEA)st (Equation (24)) c |
|---|---|---|---|---|---|---|---|
| bpy | 29.20 ± 4.87 | 96.69 ± 0.53 | 3.31 ± 0.53 | 2.89 ± 0.68 | 26.31 ± 4.92 | 10 ± 3 | 87 ± 3 (21) |
| phen | 53.95 ± 8.86 | 98.18 ± 0.29 | 1.82 ± 0.29 | 3.17 ± 0.69 | 50.78 ± 8.89 | 6 ± 2 | 92 ± 2 (25) |
| No. | % Dioxane (v/v) | mol Fraction | ε b | log ΔCu(PME) Equation (12) | KI Equations (6) and (10) | % Cu(PME)cl Equation (14) |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 78.5 | 0.48 ± 0.07 | 2.02 ± 0.47 | 67 ± 5 |
| 2 | 30 | 0.083 | 52.7 | 0.39 ± 0.04 | 1.45 ± 0.24 | 59 ± 4 |
| 3 | 50 | 0.175 | 35.2 | 0.41 ± 0.07 | 1.57 ± 0.40 | 61 ± 6 |
| Solvent | |||||
|---|---|---|---|---|---|
| No. | System | Water | 30% Diox. a | 50% Diox. a | Comments |
| (1.a) | phen (self.) | 31.1 ± 3.4 | 2.63 ± 0.44 | 0.63 ± 0.13 | 1H NMR; D2O b,c |
| (1.b) | bpy (self.) | 7.4 ± 2.3 | 0.86 ± 0.21 | 0.38 ± 0.06 | 1H NMR; D2O b,c |
| (2.a) | (phen)(ATP)4− | 26.8 ± 7.4 (38) | 4.1 ± 1.1 (4.8) | 1.6 ± 0.7 (1.8) | 1H NMR; D2O c,d |
| (2.b) | (bpy)(ATP)4− | 13.6 ± 3.9 (16) | 3 ± 2 (3.5) | 0.3 ± 0.2 (0.4) | 1H NMR; D2O c,d |
| (3.a) | Cu(phen)(ATP)2− | 0.56 ± 0.08 | –0.03 ± 0.05 | –0.41 ± 0.09 | Pot. e,f |
| (3.b) | Cu(bpy)(ATP)2− | 0.33 ± 0.04 | –0.14 ± 0.05 | –0.46 ± 0.07 | Pot. e,f |
| (4.a) | Cu(UTP)2− | 5.81 ± 0.06 | 6.16 ± 0.05 | 6.24 ± 0.03 | Pot. f,g |
| (4.b) | Cu(ATP)2− | 6.32 ± 0.04 | 6.40 ± 0.05 | 6.34 ± 0.05 | Pot. f,g |
| ADc | % (v/v) Dioxane | log | log | log ΔCu(AD) | KI | % Cu(AD)cl |
|---|---|---|---|---|---|---|
| AMP2− | 0 | 3.14 ± 0.01 | 2.87 ± 0.08 | 0.27 ± 0.08 | 0.86 ± 0.35 | 46 ± 10 |
| 20 | 3.56 ± 0.01 | 3.49 ± 0.04 | 0.07 ± 0.04 | 0.17 ± 0.11 | 15 ± 8 | |
| 30 | 3.86 ± 0.02 | 3.82 ± 0.03 | 0.04 ± 0.04 | 0.10 ± 0.09 | 9 ± 8 | |
| 40 | 4.30 ± 0.02 | 4.19 ± 0.06 | 0.11 ± 0.06 | 0.29 ± 0.19 | 22 ± 11 | |
| 50 | 4.73 ± 0.04 | 4.45 ± 0.02 | 0.28 ± 0.04 | 0.91 ± 0.20 | 48 ± 5 | |
| PMEA2− | 0 | 3.96 ± 0.04 | 3.19 ± 0.06 | 0.77 ± 0.07 | 4.89 ± 0.98 | 83 ± 3 (49 ± 10) c |
| 30 | 4.70 ± 0.05 | 4.18 ± 0.03 | 0.52 ± 0.06 | 2.31 ± 0.44 | 70 ± 4 (26 ± 10) c | |
| 50 | 5.54 ± 0.07 | 4.79 ± 0.03 | 0.75 ± 0.08 | 4.62 ± 0.99 | 82 ± 3 (54 ± 9) c |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sigel, A.; Sigel, H.; Sigel, R.K.O. Coordination Chemistry of Nucleotides and Antivirally Active Acyclic Nucleoside Phosphonates, including Mechanistic Considerations. Molecules 2022, 27, 2625. https://doi.org/10.3390/molecules27092625
Sigel A, Sigel H, Sigel RKO. Coordination Chemistry of Nucleotides and Antivirally Active Acyclic Nucleoside Phosphonates, including Mechanistic Considerations. Molecules. 2022; 27(9):2625. https://doi.org/10.3390/molecules27092625
Chicago/Turabian StyleSigel, Astrid, Helmut Sigel, and Roland K. O. Sigel. 2022. "Coordination Chemistry of Nucleotides and Antivirally Active Acyclic Nucleoside Phosphonates, including Mechanistic Considerations" Molecules 27, no. 9: 2625. https://doi.org/10.3390/molecules27092625
APA StyleSigel, A., Sigel, H., & Sigel, R. K. O. (2022). Coordination Chemistry of Nucleotides and Antivirally Active Acyclic Nucleoside Phosphonates, including Mechanistic Considerations. Molecules, 27(9), 2625. https://doi.org/10.3390/molecules27092625