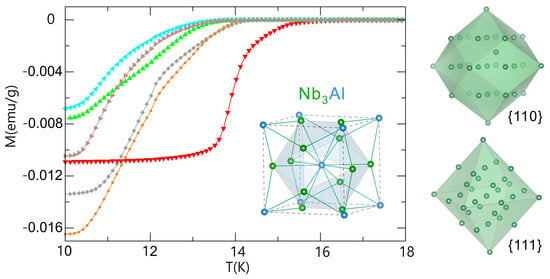
The Preparation of a Challenging Superconductor Nb3Al by Exploiting Nano Effect
Abstract
:1. Introduction
2. Results and Discussion
2.1. Experimental
2.1.1. Preparation of Reactive Nb Samples
2.1.2. Synthesis of Nb3Al
2.2. Theoretical Section
3. Materials and Methods
3.1. Synthesis
3.2. Characterization
3.3. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Kuroda, T.; Wada, H.; Bray, S.L.; Ekin, J.W. Critical-current degradation in Nb3Al wires due to axial and transverse stress. Fusion Eng. Des. 1993, 20, 271–275. [Google Scholar] [CrossRef]
- Ayai, N.; Yamada, Y.; Mikumo, A.; Takahashi, K.; Sato, K.; Koizumi, N.; Sugimoto, M.; Ando, T.; Takahashi, Y.; Nishi, M. Development of Nb3Al multifilamentary superconductors. IEEE Trans. Appl. Supercon. 1995, 5, 893–896. [Google Scholar] [CrossRef]
- Dew-Hughes, D.; Luhman, T. Treatise on Materials Science & Technology: Metallurgy of Superconducting Materials; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Pan, X.; Yan, G.; Cui, L.; Chen, C.; Bai, Z.; Li, C.; Chen, Y.; Zhao, Y.; Liu, X.; Feng, Y.; et al. Fabrication and superconducting properties of rod-in-tube multifilamentary Nb3Al wire with rapid heating and quenching heat-treatment. IEEE Trans. Appl. Supercon. 2014, 25, 1–4. [Google Scholar] [CrossRef]
- Takeuchi, T. Nb3Al conductors for high-field applications. Supercond. Sci. Technol. 2000, 13, R101–R119. [Google Scholar] [CrossRef]
- Kuroda, T.; Katagiri, K.; Kodaka, H.; Yuyama, M.; Wada, H.; Inoue, K. Superconducting properties of neutron irradiated Nb3Al multifilamentary wires fabricated by the Nb-tube process. Phys. B 1996, 216, 230–232. [Google Scholar] [CrossRef]
- Ayai, N.; Yamada, Y.; Mikumo, A.; Ito, M.; Ohmatsu, K.; Sato, K.; Koizumi, N.; Ando, T.; Matsui, K.; Sugimoto, M.; et al. Development of Nb3Al superconductors for ITER. IEEE Trans. Appl. Supercon. 1999, 9, 2688–2691. [Google Scholar] [CrossRef]
- Koizumi, N.; Takeuchi, T.; Okuno, K. Development of advanced Nb3Al superconductors for a fusion demo plant. Nucl. Fusion 2005, 45, 431–438. [Google Scholar] [CrossRef]
- Ceresara, S.; Ricci, M.; Sacchetti, N.; Sacerdoti, G. Nb3Al formation at temperatures lower than 1000° C. IEEE Trans. Magn. 1975, 11, 263–265. [Google Scholar] [CrossRef]
- Cui, L.J.; Yan, G.; Pan, X.F.; Zhang, P.X.; Qi, M.; Liu, X.H.; Feng, Y.; Chen, Y.L.; Zhao, Y. Fabrication and superconducting properties of a simple-structured jelly-roll Nb3Al wire with low-temperature heat-treatment. Phys. C 2015, 513, 24–28. [Google Scholar] [CrossRef]
- Takeuchi, T.; Kuroda, T.; Itoh, K.; Kosuge, M.; Iijima, Y.; Kiyoshi, T.; Matsumoto, F.; Inoue, K. Development of Nb tube processed Nb3Al multifilamentary superconductor. J. Fusion Energ. 1992, 11, 7–18. [Google Scholar] [CrossRef]
- Saito, S.; Ikeda, K.; Ikeda, S.; Nagata, A.; Noto, K. A new fabrication process of Nb3Al superconducting wires using clad-chips. Mater. Trans. JIM 1990, 31, 415–420. [Google Scholar] [CrossRef]
- Zhang, W.; Li, P.; Zou, X.; Yu, Z.; Yang, X.; Pan, X.; Zhao, Y.; Zhang, Y. Equiaxial nano-crystals Nb3Al superconductor prepared by optimized mechanically alloying. J. Mater. Sci. 2019, 54, 5022–5031. [Google Scholar] [CrossRef]
- Qi, M.; Sun, Y.Y.; Pan, X.F.; Zhang, P.X.; Cui, L.J.; Li, C.S.; Yan, G. Fabrication of Nb3Al superconducting wires by the mechanical alloying method. IEEE Trans. Appl. Supercon. 2015, 25, 1–5. [Google Scholar] [CrossRef]
- Takeuchi, T. Nb3Al conductors-rapid-heating, quenching and transformation process. IEEE Trans. Appl. Supercond. 2000, 10, 1016–1021. [Google Scholar] [CrossRef]
- Li, X.; Wen, X.; Du, Z.; Khan, A.; Ma, Z. Enhanced critical current density in Nb3Al superconductor by optimizing mechanical alloying and subsequent sintering process. Mater. Chem. Phys. 2021, 259, 123955. [Google Scholar] [CrossRef]
- Schaper, W.; Kehlenbeck, M.; Zimmermann, I.; Freyhardt, H. Comparison of Al5-Nb3Al superconductors produced by laser alloying and infiltration. IEEE Trans. Magn. 1989, 25, 1988–1991. [Google Scholar] [CrossRef]
- Kumakura, H.; Togano, K.; Tachikawa, K.; Tsukamoto, S.; Irie, H. Fabrication of Nb3Al and Nb3(Al,Ge) superconducting composite tapes by electron beam irradiation. Appl. Phys. Lett. 1986, 49, 46–48. [Google Scholar] [CrossRef]
- Kikuchi, A.; Iijima, Y.; Inoue, K. Microstructures of rapidly-heated/quenched and transformed Nb3Al multifilamentary superconducting wires. IEEE Trans. Appl. Supercon. 2001, 11, 3615–3618. [Google Scholar] [CrossRef]
- Völkl, J.; Alefeld, G. Hydrogen in Metals I: Basic Properties; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1978. [Google Scholar]
- Schober, H.R.; Stoneham, A.M. Diffusion of hydrogen in niobium. Phys. Rev. Lett. 1988, 60, 2307–2310. [Google Scholar] [CrossRef]
- Nakamura, Y.; Livshits, A.I.; Nakahara, Y.; Hatano, Y.; Busnyuk, A.; Ohyabu, N. Hydrogen absorption capability of a niobium panel for pumping neutral atoms in divertor region. J. Nucl. Mater. 2005, 337, 461–465. [Google Scholar] [CrossRef]
- Martínez, A.; Santos, D. Influence of the substitution of V by Nb in the structure and properties of hydrogen absorption/desorption of TiCr1.1V0.9 alloy. J. Alloy. Compd. 2012, 536, S231–S235. [Google Scholar] [CrossRef]
- Nyahuma, F.M.; Zhang, L.T.; Song, M.C.; Lu, X.; Xiao, B.B.; Zheng, J.G.; Wu, F.Y. Significantly improved hydrogen storage behaviors in MgH2 with Nb nanocatalyst. Int. J. Miner. Metall. Mater. 2022, 29, 1788–1797. [Google Scholar] [CrossRef]
- Rao, J.P.; Ouyang, C.Y.; Lei, M.S.; Jiang, F.Y. First principles investigation of interaction between interstitials H atom and Nb metal. Acta Phys. Sin. 2012, 61, 047105. [Google Scholar]
- Rao, J.P.; Ouyang, C.Y.; Lei, M.S.; Jiang, F.Y. Vacancy and H Interactions in Nb. Chin. Phys. Lett. 2011, 28, 127101. [Google Scholar] [CrossRef]
- Skatkov, L.; Cheremskoy, P. Pore structure of sintered niobium after reaction with hydrogen and nitrogen. Powder Metall. 2000, 43, 182–184. [Google Scholar] [CrossRef]
- Johnson, L.; Dresser, M.; Donaldson, E. Adsorption and absorption of hydrogen by niobium. J. Vac. Sci. Technol. 1972, 9, 857–860. [Google Scholar] [CrossRef]
- Ford, D.C.; Cooley, L.D.; Seidman, D.N. First-principles calculations of niobium hydride formation in superconducting radio-frequency cavities. Supercond. Sci. Technol. 2013, 26, 095002. [Google Scholar] [CrossRef]
- Aleksanyan, A.; Dolukhanyan, S. Combustion of niobium in hydrogen and nitrogen. Synthesis of niobium hydrides and hydridonitrides. Int. J. Hydrogen Energy 2001, 26, 429–433. [Google Scholar] [CrossRef]
- Reilly, J.J.; Wiswall, R.H. Higher hydrides of vanadium and niobium. Inorg. Chem. 1970, 9, 1678–1682. [Google Scholar] [CrossRef]
- Pöttgen, R.; Jüstel, T.; Strassert, C.A. (Eds.) Rare Earth Chemistry; Walter de Gruyter GmbH & Co. KG: Berlin, Germany, 2020; pp. 511–524. [Google Scholar]
- Li, X.; Ohsaki, K.; Morita, Y.; Uda, M. Preparation of fine Nb3Al powder by hydriding and dehydriding of bulk material. J. Alloy. Compd. 1995, 227, 141–144. [Google Scholar] [CrossRef]
- Li, X.; Chiba, A.; Nakata, Y.; Nagai, H.; Suzuki, M. Characterization of ultrafine SiC-Si3N4 composite powder after heat-treatment in Ar+N2. Mater. Sci. Eng. 1996, A219, 95–101. [Google Scholar]
- Li, X.; Chiba, A.; Sato, M.; Takashash, S. Strength and superconductivity of Nb3Al prepared by spark plasma sintering. J. Alloy. Compd. 2002, 336, 232–236. [Google Scholar] [CrossRef]
- Dolukhanyana, S.K.; Ter-Galstyan, O.P.; Aleksanyan, A.G.; Hakobyan, A.G.; Mnatsakanyan, N.L.; Shekhtman, V.S. Study of the formation of niobium aluminides in the hydride cycle. Russ. J. Phys. Chem. B 2015, 9, 702–709. [Google Scholar] [CrossRef]
- Patterson, A.L. The Scherrer formula for X-ray particle size determination. Phys. Rev. 1939, 56, 978–982. [Google Scholar] [CrossRef]
- Hickmott, T.W. Problem of measuring hydrogen pressure in ultrahigh-vacuum systems. J. Vac. Sci. Technol. 1965, 2, 257–258. [Google Scholar] [CrossRef]
- Hosoda, H.; Tabaru, T.; Semboshi, S.; Hanada, S. Hydrogen absorption of Nb-Al alloy bulk specimens. J. Alloy. Compd. 1998, 281, 268–274. [Google Scholar] [CrossRef]
- Kim, H.S.; Kum, D.; Hanada, S. Structural evolution during mechanical alloying and annealing of a Nb-25at%Al alloy. J. Mater. Sci. 2000, 35, 235–239. [Google Scholar] [CrossRef]
- Abe, Y.; Hanada, S.; Saito, S.; Hirano, K.; Kobayashi, N. Compositions at Nb3Al phase boundaries at 1873 K in the Nb-Al binary phase diagram. Scripta Metal. Mater. 1995, 32, 27–30. [Google Scholar] [CrossRef]
- Wen, X.; Li, X.H.; Zhao, H.H.; Ma, Z.Q.; Yu, L.M.; Li, C.; Liu, C.X.; Guo, Q.Y.; Liu, Y.C. The phase formation mechanism of Nb3Al prepared by mechanical alloying and subsequent sintering and its effect on superconducting properties. Intermetallics 2018, 103, 33–39. [Google Scholar] [CrossRef]
- Aiken, J.D.; Finke, R.G. A review of modern transition-metal nanoclusters: Their synthesis, characterization, and applications in catalysis. J. Mol. Catal. A Chem. 1999, 145, 1–44. [Google Scholar] [CrossRef]
- Zhou, G.B.; Yang, Z.; Fu, F.J.; Hu, N.; Chen, X.S.; Tao, D.J. Melting mechanism and structure evolution of Au nanofilms explored by molecular dynamics simulations. Chin. Chem. Phys. 2015, 28, 623–629. [Google Scholar] [CrossRef]
- Zeidler, E. Applied Functional Analysis: Main Principles and Their Applications; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Ter Haar, D. Elements of Statistical Mechanics; Elsevier: New York, NY, USA, 1995. [Google Scholar]
- Huang, K. Statistical Mechanics; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Nagae, T.; Nose, M.; Yokota, M.; Saji, S.; Sekihara, H.; Doi, Y. Spark plasma sintering of Nb3Al alloy powder by MA and PMGA method. J. Jpn. Soc. Powder Powder Metall. 1996, 43, 1198–1202. [Google Scholar] [CrossRef]
- Huang, K. Quantum Field Theory: From Operators to Path Integrals; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Roberge, R. Lattice-parameter of niobium between 4.2 and 300 k. J. Less-Common Met. 1975, 40, 161–164. [Google Scholar] [CrossRef]
- Woodruff, D. Surface Alloys and Alloy Surfaces; Elsevier: New York, NY, USA, 2002. [Google Scholar]
- Fiorentini, V.; Methfessel, M. Extracting convergent surface energies from slab calculations. J. Phys.-Condens. Matter. 1996, 8, 6525–6529. [Google Scholar] [CrossRef]
- Yang, Z.; Gong, X.; Chen, Y.; Huang, J.; Lin, Y.; Luo, Z.; Deng, S.; Huang, Y. The growth of a large GdPO4 crystal guided by theoretical simulation and the study of its phonon properties. Phys. Chem. Chem. Phys. 2021, 23, 22515–22525. [Google Scholar] [CrossRef]
- Siao, M.; Shen, W.; Chen, R.; Chang, Z.; Shih, M.; Chiu, Y.; Cheng, C.-M. Two-dimensional electronic transport and surface electron accumulation in MoS2. Nat. Commun. 2018, 9, 1442. [Google Scholar] [CrossRef]
- Li, S.; Zhao, X.; Xu, X.; Gao, Y.; Zhang, Z. Stacking principle and magic sizes of transition metal nanoclusters based on generalized Wulff construction. Phys. Rev. Lett. 2013, 111, 115501. [Google Scholar] [CrossRef] [PubMed]
- Munitz, A.; Gokhale, A.B.; Abbaschian, R. The effect of supercooling on the microstructure of Al-Nb alloys. J. Mater. Sci. 2000, 35, 2263–2271. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, C.; Cheng, X.; Gao, X.; Köhler, J.; Deng, S. The Preparation of a Challenging Superconductor Nb3Al by Exploiting Nano Effect. Molecules 2023, 28, 6455. https://doi.org/10.3390/molecules28186455
Luan C, Cheng X, Gao X, Köhler J, Deng S. The Preparation of a Challenging Superconductor Nb3Al by Exploiting Nano Effect. Molecules. 2023; 28(18):6455. https://doi.org/10.3390/molecules28186455
Chicago/Turabian StyleLuan, Chengkai, Xiyue Cheng, Xiuping Gao, Jürgen Köhler, and Shuiquan Deng. 2023. "The Preparation of a Challenging Superconductor Nb3Al by Exploiting Nano Effect" Molecules 28, no. 18: 6455. https://doi.org/10.3390/molecules28186455
APA StyleLuan, C., Cheng, X., Gao, X., Köhler, J., & Deng, S. (2023). The Preparation of a Challenging Superconductor Nb3Al by Exploiting Nano Effect. Molecules, 28(18), 6455. https://doi.org/10.3390/molecules28186455