The Nature of the Chemical Bonds of High-Valent Transition–Metal Oxo (M=O) and Peroxo (MOO) Compounds: A Historical Perspective of the Metal Oxyl–Radical Character by the Classical to Quantum Computations
Abstract
:1. Introduction
2. Historical Backgrounds for Mono-Oxygenation Reactions
2.1. Discoveries of Cytochrome P450 Enzymes and Related Metalloenzymes

2.2. Isolobal and Isospin Analogy between Organic and Inorganic Peroxides


3. Ab Initio Calculations of Metal Oxo and Peroxide Complexes
3.1. Ab Initio Calculations of Metal Peroxide Complexes

3.2. Ab Initio Calculations of Metal Oxo Complexes

3.3. Comparisons among UHF, UCCSD(T), and Hybrid DFT Computational Results
4. Orbital Bifurcations for Radical Reactions and Derivations of Chemical Indices
4.1. HOMO-LUMO Mixing for Homolytic and Electron-Transfer Diradicals by BS Models

4.2. Four Different Mechanisms of Chemical Reactions by BS Models
4.3. Derivations of Effective Bond Orders for Fe(IV)=O and Fe(V)=O Bonds

4.4. Reduction of Effective Bond Order and Radical Reactivity of High-Valent Fe=O

4.5. Isolobal and Isospin Analogy among Fe(IV)=O, O=O, and O for Chemical Reactions



4.6. Quantum Resonance between BS Solutions (RBS) and Diradical Character

4.7. Spin Density and Pair and Spin Correlation Functions for Singlet Diradicals


4.8. Quantum Spin Hamiltonian Models for Compound I (Cpd I)


4.9. Charge and Spin Correlation Diagrams for Mono-Oxygenations by Cpd I
2(4)[Por(+•↓(↑)) ↑•Fe(III)-OH…↑•R]
→ 2[Por ↑↑↑•••Fe(III)-OH…↓•R]
4.10. Mono-Oxygenations by Nonheme Iron-Oxo Compounds
→ 5[↑↑↑•••Fe(III)-O-H…↑•R]
→ 5[↑↑↑↑••••Fe(III)-HO↑•(π)…↓•R] → 5[↑↑↑↑••••Fe(III)-HO-R]
→ 5[↑↑↑↑↑•••••Fe(III)-O-H…↓•R]

4.11. Quantum Spin Hamiltonian Models for Binuclear Transition Metal Oxides

5. Theoretical Investigations of Mono-Oxygenation Reactions by P450 and Related Species
5.1. Natural Orbital Analysis of the BS Solutions and Chemical Indices of the Intermediates

5.2. Confirmations of the Models of Mono-Oxygenation Reactions by Ab Initio Calculations


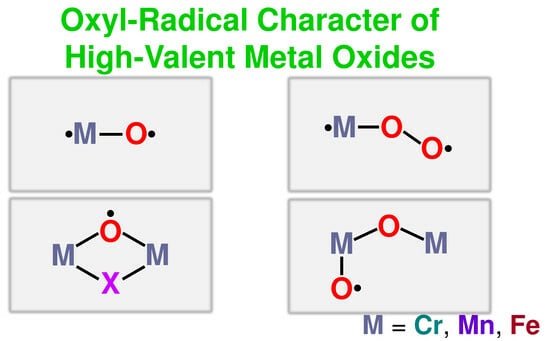
5.3. The Oxyl-Radical Character of the High-Valent Fe(V)=O Bonds
5.4. Mono-Oxygenation by the Non-Heme High-Valent Fe(IV)=O Bonds
5.5. Reduction of the Activation Barriers for Mono-Oxygenations
6. The Computational Results for Beyond HDFT Results
6.1. Beyond BS Computations

6.2. CASPT2 and RASPT2 Results for Iron-Oxo Compound
- Use of large active space for construction of the reference states for MR methods;
- Use of flexible basis sets for inclusion of dynamical correlation effects;
- Dynamical correlation corrections by higher-order methods than the PT2 level.
6.3. Beyond HDFT Computations for Non-Heme Iron-Oxo Compounds
6.4. Future Perspective and Outlook for Quantum Computations

Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
A.1. Localized Natural Orbitals (LNO)
A.2. Resonating BS (RBS) Method and Exchange Coupling
References
- Klingenberg, M. Pigments of rat liver microsomes. Arch. Biochem. Biophys. 1958, 75, 376–386. [Google Scholar] [CrossRef] [PubMed]
- Omura, T.; Sato, R. A new cytochrome in liver microsomes. J. Biol. Chem. 1962, 237, PC1375–PC1376. [Google Scholar] [CrossRef]
- Estabrook, R.W.; Cooper, D.Y.; Rosenthal, O. The light reversible carbon monoxide inhibition of the steroid C21-hydroxylase system of the adrenal cortex. Biochem. Z. 1963, 338, 741–755. [Google Scholar] [PubMed]
- Cooper, D.Y.; Estabrook, R.W.; Rosenthal, O. The stoichiometry of C21 hydroxylation of steroids by adrenocortical microsomes. J. Biol. Chem. 1963, 238, 1320–1323. [Google Scholar] [CrossRef] [PubMed]
- Omura, T.; Sato, R. Fractional solubilization of haemoproteins and partial purification of carbon monoxide-binding cytochrome from liver microsomes. Biochim. Biophys. Acta 1963, 71, 224–226. [Google Scholar] [CrossRef] [PubMed]
- Omura, T.; Sato, R. The carbon monoxide-binding pigment of liver microsomes: I. Evidence for its hemoprotein nature. J. Biol. Chem. 1964, 239, 2370–2378. [Google Scholar] [CrossRef]
- Omura, T.; Sato, R. The carbon monoxide-binding pigment of liver microsomes: II. Solubilization, purification, and properties. J. Biol. Chem. 1964, 239, 2379–2385. [Google Scholar] [CrossRef]
- Cooper, D.Y.; Levin, S.; Narasimhulu, S.; Rosenthal, O.; Estabrook, R.W. Photochemical action spectrum of the terminal oxidase of mixed function oxidase systems. Science 1965, 147, 400–402. [Google Scholar] [CrossRef]
- Omura, T.; Sanders, T.E.; Estabrook, R.W.; Cooper, D.Y.; Rosenthal, O. Isolation from adrenal cortex of a nonheme iron protein and a flavoprotein functional as a reduced triphosphopyridine nucleotide-cytochrome P-450 reductase. Arch. Biochem. Biophys. 1966, 117, 660–673. [Google Scholar] [CrossRef]
- Lu, A.Y.H.; Coon, M.J. Role of hemoprotein P-450 in fatty acid ω-hydroxylation in a soluble enzyme system from liver microsomes. J. Biol. Chem. 1968, 243, 1331–1332. [Google Scholar] [CrossRef]
- Katagiri, M.; Ganguli, B.N.; Gunsalus, I.C. A soluble cytochrome P-450 functional in methylene hydroxylation. J. Biol. Chem. 1968, 243, 3543–3546. [Google Scholar] [CrossRef]
- Guengerich, F.P. Separation and purification of multiple forms of microsomal cytochrome P-450. Partial characterization of three apparently homogeneous cytochromes P-450 prepared from livers of phenobarbital- and 3-methylcholanthrene-treated rats. J. Biol. Chem. 1978, 253, 7931–7939. [Google Scholar] [CrossRef] [PubMed]
- Black, S.D.; Coon, M.J. Comparative structures of P-450 cytochromes. In Cytochrome P-450: Structure, Mechanism, and Biochemistry; Ortiz de Montellano, R.R., Ed.; Plenum Press: New York, NY, USA, 1986; pp. 161–216. [Google Scholar]
- Dawson, J.H.; Sono, M. Cytochrome P-450 and chloroperoxidase: Thiolate-ligated heme enzymes. Spectroscopic determination of their active-site structures and mechanistic implications of thiolate ligation. Chem. Rev. 1987, 87, 1255–1276. [Google Scholar] [CrossRef]
- Tabushi, I. Reductive dioxygen activation by use of artificial P-450 systems. Coord. Chem. Rev. 1988, 86, 1–42. [Google Scholar] [CrossRef]
- Meunier, B. Metalloporphyrins as versatile catalysts for oxidation reactions and oxidative DNA cleavage. Chem. Rev. 1992, 92, 1411–1456. [Google Scholar] [CrossRef]
- Feig, A.L.; Lippard, S.J. Reactions of non-heme iron(II) centers with dioxygen in biology and chemistry. Chem. Rev. 1994, 94, 759–805. [Google Scholar] [CrossRef]
- Sono, M.; Roach, M.P.; Coulter, E.D.; Dawson, J.H. Heme-containing oxygenases. Chem. Rev. 1996, 96, 2841–2888. [Google Scholar] [CrossRef]
- Omura, T.; Ishimura, Y.; Fujii-Kuriyama, Y. Cytochrome P-450, 2nd ed.; Kodansha: Tokyo, Japan, 1993. [Google Scholar]
- Li, H. Cytochrome P450. In Handbook of Metalloproteins; Messerschmidt, A., Huber, R., Poulos, T., Wieghardt, K., Eds.; Wiley: Oxford, UK, 2001; pp. 267–282. [Google Scholar]
- Ortiz de Montellano, P.R. Cytochrome P450 Structure, Mechanism, and Biochemistry, 3rd ed.; Kluwer-Academic: New York, NY, USA, 2005. [Google Scholar]
- Hayaishi, O.; Hashimoto, K. Pyrocatecase a new enzyme catalizing oxidative breakdown of pyrocatechin. J. Biochem. 1950, 37, 371–374. [Google Scholar] [CrossRef]
- Hayaishi, O.; Katagiri, M.; Rothberg, S. Studies on oxygenases: Pyrocatechase. J. Biol. Chem. 1957, 229, 905–920. [Google Scholar] [CrossRef]
- Mason, H.S. Mechanisms of oxygen metabolism. Science 1957, 125, 1185–1188. [Google Scholar] [CrossRef]
- Yamaguchi, K. Instability in Chemical Bonds—SCF, APUMP, APUCC, MR-CI and MR-CC Approaches. In Self-Consistent Field: Theory and Applications; Carbó, R., Klobukowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 727–823. [Google Scholar]
- Yamaguchi, K. Symmetry and broken symmetry in molecular orbital (MO) descriptions of unstable molecules. Generalized MO theoretical studies on 1,3-dipolar species. J. Mol. Struct. Theochem. 1983, 103, 101–120. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T. Ab-initio molecular orbital studies of structure and reactivity of transition metal-oxo compounds. In Applied Quantum Chemistry; Smith, V.H., Jr., Schaefer, H.F., III, Morokuma, K., Eds.; D. Reidel Pub. Com.: Lancaster, UK, 1986; pp. 155–184. [Google Scholar]
- Yamaguchi, K.; Tsunekawa, T.; Toyoda, Y.; Fueno, T. Ab initio molecular orbital calculations of effective exchange integrals between transition metal ions. Chem. Phys. Lett. 1988, 143, 371–376. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T. Ab initio MO studies on structure and reactivity of superoxo transition-metal complexes. In The Role of Oxygen in Chemistry and Biology; Ando, W., Morooka, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 1988; pp. 263–268. [Google Scholar]
- Yamaguchi, K.; Takahara, Y.; Fueno, T.; Saito, I.; Matsuura, T. Ab initio MO studies on structure and reactivity of transition metal hydroperoxides. In Medical, Biochemical and Chemical Aspects of Free Radicals; Hayaishi, O., Niki, E., Kondo, M., Yoshikawa, T., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; pp. 993–996. [Google Scholar]
- Roos, B.O. The complete active space SCF method in a Fock-matrix-based super-CI formulation. Int. J. Quant. Chem. 1980, 18, 175–189. [Google Scholar] [CrossRef]
- Yamaguchi, K. Multireference (MR) configuration interaction (CI) approach for quasidegenerate systems. Int. J. Quant. Chem. 1980, 18, 269–284. [Google Scholar] [CrossRef]
- Aspuru-Guzik, A.; Dutoi, A.D.; Love, P.J.; Head-Gordon, M. Simulated quantum computation of molecular energies. Science 2005, 309, 1704–1707. [Google Scholar] [CrossRef]
- Reiher, M.; Wiebe, N.; Svore, K.M.; Wecker, D.; Troyer, M. Elucidating reaction mechanisms on quantum computers. Proc. Natl. Acad. Sci. USA 2017, 114, 7555–7560. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Dattani, N.S.; Umrigar, C.J.; Chan, G.K.-L. The electronic complexity of the ground-state of the FeMo cofactor of nitrogenase as relevant to quantum simulations. J. Chem. Phys. 2019, 150, 024302. [Google Scholar] [CrossRef]
- Miyagawa, K.; Shoji, M.; Isobe, H.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Theory of chemical bonds in metalloenzymes XXIV electronic and spin structures of FeMoco and Fe-S clusters by classical and quantum computing. Mol. Phys. 2020, 118, e1760388. [Google Scholar] [CrossRef]
- Theorell, H.; Ehrenberg, A.; Chance, B. Electronic structure of the peroxidase-peroxide complexes. Arch. Biochem. Biophys. 1952, 37, 237–239. [Google Scholar] [CrossRef]
- Yonetani, T.; Schleyer, H.; Ehrenberg, A. Studies on cytochrome c peroxidase VII. Electron paramagnetic resonance absorptions of the enzyme and complexes in dissolved and crystalline forms. J. Biol. Chem. 1966, 241, 3240–3243. [Google Scholar] [CrossRef]
- Iizuka, T.; Kotani, M.; Yonetani, T. A thermal equilibrium between high- and low-spin states in ferric cytochrome c peroxidase and some discussion on the enzyme substrate complex. Biochim. Biophys. Acta Enzym. 1968, 167, 257–267. [Google Scholar] [CrossRef] [PubMed]
- Moss, T.H.; Ehrenberg, A.; Bearden, A.J. Mössbauer spectroscopic evidence for the electronic configuration of iron in horseradish peroxidase and its peroxide derivatives. Biochemistry 1969, 8, 4159–4162. [Google Scholar] [CrossRef] [PubMed]
- Dolphin, D.; Forman, A.; Borg, D.C.; Fajer, J.; Felton, R.H. Compounds I of catalase and horse radish peroxidase: π-cation radicals. Proc. Natl. Acad. Sci. USA 1971, 68, 614–618. [Google Scholar] [CrossRef] [PubMed]
- Groves, J.T.; McClusky, G.A. Aliphatic hydroxylation via oxygen rebound. Oxygen transfer catalyzed by iron. J. Am. Chem. Soc. 1976, 98, 859–861. [Google Scholar] [CrossRef]
- Yokota, K.; Yamazaki, I. Analysis and computer simulation of aerobic oxidation of reduced nicotinamide adenine dinucleotide catalyzed by horseradish peroxidase. Biochemistry 1977, 16, 1913–1920. [Google Scholar] [CrossRef]
- Chance, B.; Sies, H.; Boveris, A. Hydroperoxide metabolism in mammalian organs. Physiol. Rev. 1979, 59, 527–605. [Google Scholar] [CrossRef]
- Groves, J.T.; Nemo, T.E.; Myers, R.S. Hydroxylation and epoxidation catalyzed by iron-porphine complexes. Oxygen transfer from iodosylbenzene. J. Am. Chem. Soc. 1979, 101, 1032–1033. [Google Scholar] [CrossRef]
- Solomon, E.I.; Hare, J.W.; Dooley, D.M.; Dawson, J.H.; Stephens, P.J.; Gray, H.B. Spectroscopic studies of stellacyanin, plastocyanin, and azurin. Electronic structure of the blue copper sites. J. Am. Chem. Soc. 1980, 102, 168–178. [Google Scholar] [CrossRef]
- Sheldon, R.; Kochi, J.K. Metal-Catalyzed Oxidations of Organic Compounds; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Groves, J.T.; Haushalter, R.C.; Nakamura, M.; Nemo, T.E.; Evans, B.J. High-valent iron-porphyrin complexes related to peroxidase and cytochrome P-450. J. Am. Chem. Soc. 1981, 103, 2884–2886. [Google Scholar] [CrossRef]
- Groves, J.T.; Nemo, T.E. Epoxidation reactions catalyzed by iron porphyrins. Oxygen transfer from iodosylbenzene. J. Am. Chem. Soc. 1983, 105, 5786–5791. [Google Scholar] [CrossRef]
- Groves, J.T.; Myers, R.S. Catalytic asymmetric epoxidations with chiral iron porphyrins. J. Am. Chem. Soc. 1983, 105, 5791–5796. [Google Scholar] [CrossRef]
- Groves, J.T.; Nemo, T.E. Aliphatic hydroxylation catalyzed by iron porphyrin complexes. J. Am. Chem. Soc. 1983, 105, 6243–6248. [Google Scholar] [CrossRef]
- Chance, B.; Powers, L.; Ching, Y.; Poulos, T.; Schonbaum, G.R.; Yamazaki, I.; Paul, K.G. X-ray absorption studies of intermediates in peroxidase activity. Arch. Biochem. Biophys. 1984, 235, 596–611. [Google Scholar] [CrossRef] [PubMed]
- Groves, J.T.; Adhyam, D.V. Hydroxylation by cytochrome P-450 and metalloporphyrin models. Evidence for allylic rearrangement. J. Am. Chem. Soc. 1984, 106, 2177–2181. [Google Scholar] [CrossRef]
- Groves, J.T.; Quinn, R.; McMurry, T.J.; Lang, G.; Boso, B. Iron(IV) porphyrins from iron(III) porphyrin cation radicals. J. Chem. Soc. Chem. Commun. 1984, 21, 1455–1456. [Google Scholar] [CrossRef]
- Tabushi, I.; Kodera, M.; Yokoyama, M. Kinetics and mechanism of reductive dioxygen activation catalyzed by P-450 model system. Iron picket fence as a catalytic center. J. Am. Chem. Soc. 1985, 107, 4466–4473. [Google Scholar] [CrossRef]
- Groves, J.T. Key elements of the chemistry of cytochrome P-450: The oxygen rebound mechanism. J. Chem. Educ. 1985, 62, 928–931. [Google Scholar] [CrossRef]
- Penner-Hahn, J.E.; Eble, K.S.; McMurry, T.J.; Renner, M.; Balch, A.L.; Groves, J.T.; Dawson, J.H.; Hodgson, K.O. Structural characterization of horseradish peroxidase using EXAFS spectroscopy. Evidence for Fe=O ligation in compounds I and II. J. Am. Chem. Soc. 1986, 108, 7819–7825. [Google Scholar] [CrossRef]
- Groves, J.T.; Watanabe, Y. The mechanism of olefin epoxidation by oxo-iron porphyrins. Direct observation of an intermediate. J. Am. Chem. Soc. 1986, 108, 507–508. [Google Scholar] [CrossRef]
- Groves, J.T.; Watanabe, Y. Reactive iron porphyrin derivatives related to the catalytic cycles of cytochrome P-450 and peroxidase. Studies of the mechanism of oxygen activation. J. Am. Chem. Soc. 1988, 110, 8443–8452. [Google Scholar] [CrossRef]
- Imai, M.; Shimada, H.; Watanabe, Y.; Matsushima-Hibiya, Y.; Makino, R.; Koga, H.; Horiuchi, T.; Ishimura, Y. Uncoupling of the cytochrome P-450cam monooxygenase reaction by a single mutation, threonine-252 to alanine or valine: Possible role of the hydroxy amino acid in oxygen activation. Proc. Natl. Acad. Sci. USA 1989, 86, 7823–7827. [Google Scholar] [CrossRef] [PubMed]
- Groves, J.T.; Viski, P. Asymmetric hydroxylation by a chiral iron porphyrin. J. Am. Chem. Soc. 1989, 111, 8537–8538. [Google Scholar] [CrossRef]
- Groves, J.T.; Viski, P. Asymmetric hydroxylation, epoxidation, and sulfoxidation catalyzed by vaulted binaphthyl metalloporphyrins. J. Org. Chem. 1990, 55, 3628–3634. [Google Scholar] [CrossRef]
- Hashimoto, S.; Mizutani, Y.; Tatsuno, Y.; Kitagawa, T. Resonance Raman characterization of ferric and ferryl porphyrin π cation radicals and the FeIV=O stretching frequency. J. Am. Chem. Soc. 1991, 113, 6542–6549. [Google Scholar] [CrossRef]
- Groves, J.T.; Gross, Z.; Stern, M.K. Preparation and reactivity of oxoiron(IV) porphyrins. Inorg. Chem. 1994, 33, 5065–5072. [Google Scholar] [CrossRef]
- Newcomb, M.; Le Tadic-Biadatti, M.-H.; Chestney, D.L.; Roberts, E.S.; Hollenberg, P.F. A nonsynchronous concerted mechanism for cytochrome P-450 catalyzed hydroxylation. J. Am. Chem. Soc. 1995, 117, 12085–12091. [Google Scholar] [CrossRef]
- Toy, P.H.; Newcomb, M.; Hollenberg, P.F. Hypersensitive mechanistic probe studies of cytochrome P450-catalyzed hydroxylation reactions. Implications for the cationic pathway. J. Am. Chem. Soc. 1998, 120, 7719–7729. [Google Scholar] [CrossRef]
- Collman, J.P.; Chien, A.S.; Eberspacher, T.A.; Brauman, J.I. Multiple active oxidants in cytochrome P-450 model oxidations. J. Am. Chem. Soc. 2000, 122, 11098–11100. [Google Scholar] [CrossRef]
- Newcomb, M.; Toy, P.H. Hypersensitive radical probes and the mechanisms of cytochrome P450-catalyzed hydroxylation reactions. Acc. Chem. Res. 2000, 33, 449–455. [Google Scholar] [CrossRef]
- Newcomb, M.; Shen, R.; Choi, S.-Y.; Toy, P.H.; Hollenberg, P.F.; Vaz, A.D.N.; Coon, M.J. Cytochrome P450-catalyzed hydroxylation of mechanistic probes that distinguish between radicals and cations. Evidence for cationic but not for radical intermediates. J. Am. Chem. Soc. 2000, 122, 2677–2686. [Google Scholar] [CrossRef]
- Newcomb, M.; Hollenberg, P.F.; Coon, M.J. Multiple mechanisms and multiple oxidants in P450-catalyzed hydroxylations. Arch. Biochem. Biophys. 2003, 409, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Groves, J.T.; Stern, M.K. Olefin epoxidation by manganese (IV) porphyrins: Evidence for two reaction pathways. J. Am. Chem. Soc. 1987, 109, 3812–3814. [Google Scholar] [CrossRef]
- Bernadou, J.; Fabiano, A.-S.; Robert, A.; Meunier, B. “Redox tautomerism” in high-valent metal-oxo-aquo complexes. origin of the oxygen atom in epoxidation reactions catalyzed by water-soluble metalloporphyrins. J. Am. Chem. Soc. 1994, 116, 9375–9376. [Google Scholar] [CrossRef]
- Pitié, M.; Bernadou, J.; Meunier, B. Oxidation at carbon-1′ of DNA deoxyriboses by the Mn-TMPyP/KHSO5 system results from a cytochrome P-450-type hydroxylation reaction. J. Am. Chem. Soc. 1995, 117, 2935–2936. [Google Scholar] [CrossRef]
- Groves, J.T.; Lee, J.; Marla, S.S. Detection and characterization of an oxomanganese(V) porphyrin complex by rapid-mixing stopped-flow spectrophotometry. J. Am. Chem. Soc. 1997, 119, 6269–6273. [Google Scholar] [CrossRef]
- Vialas, C.; Pratviel, G.; Claparols, C.; Meunier, B. Efficient oxidation of 2‘-deoxyguanosine by Mn-TMPyP/KHSO5 to imidazolone dIz without formation of 8-oxo-dG. J. Am. Chem. Soc. 1998, 120, 11548–11553. [Google Scholar] [CrossRef]
- Jin, N.; Groves, J.T. Unusual kinetic stability of a ground-state singlet oxomanganese(V) porphyrin. evidence for a spin state crossing effect. J. Am. Chem. Soc. 1999, 121, 2923–2924. [Google Scholar] [CrossRef]
- Limburg, J.; Vrettos, J.S.; Chen, H.; de Paula, J.C.; Crabtree, R.H.; Brudvig, G.W. Characterization of the O2-evolving reaction catalyzed by [(terpy)(H2O)MnIII(O)2MnIV(OH2)(terpy)](NO3)3 (terpy = 2,2′:6,2′’-terpyridine). J. Am. Chem. Soc. 2001, 123, 423–430. [Google Scholar] [CrossRef]
- Isobe, H.; Soda, T.; Kitagawa, Y.; Takano, Y.; Kawakami, T.; Yoshioka, Y.; Yamaguchi, K. EHF theory of chemical reactions V. Nature of manganese–oxygen bonds by hybrid density functional theory (DFT) and coupled-cluster (CC) methods. Int. J. Quant. Chem. 2001, 85, 34–43. [Google Scholar] [CrossRef]
- Koizumi, K.; Shoji, M.; Nishiyama, Y.; Maruno, Y.; Kitagawa, Y.; Soda, K.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. The electronic structure and magnetic property of metal-oxo, porphyrin manganese-oxo, and μ-oxo-bridged manganese porphyrin dimer. Int. J. Quant. Chem. 2004, 100, 943–956. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Shoji, M.; Isobe, H.; Miyagawa, K.; Suga, M.; Akita, F.; Shen, J.-R. Geometric, electronic and spin structures of the CaMn4O5 catalyst for water oxidation in oxygen-evolving photosystem II. Interplay between experiments and theoretical computations. Coord. Chem. Rev. 2022, 471, 214742. [Google Scholar] [CrossRef]
- Yamaguchi, K. Theoretical calculations of singlet oxygen reactions. In Singlet O2 Vol. III; Chapter 2; Frimer, A.A., Ed.; CRC Press: Boca Raton, FL, USA, 1985; pp. 119–250. [Google Scholar]
- Yamaguchi, K.; Takada, K.; Otsuji, Y.; Mizuno, K. Theoretical and general aspects of organic peroxides. In Organic Peroxides; Ando, W., Ed.; John Wiley & Sons: Chichester, UK, 1992; pp. 1–100. [Google Scholar]
- Collman, J.P.; Boulatov, R.; Sunderland, C.J.; Fu, L. Functional analogues of cytochrome c oxidase, myoglobin, and hemoglobin. Chem. Rev. 2004, 104, 561–588. [Google Scholar] [CrossRef] [PubMed]
- Meunier, B.; de Visser, S.P.; Shaik, S. Mechanism of oxidation reactions catalyzed by cytochrome P450 enzymes. Chem. Rev. 2004, 104, 3947–3980. [Google Scholar] [CrossRef]
- Denisov, I.G.; Makris, T.M.; Sligar, S.G.; Schlichting, I. Structure and chemistry of cytochrome P450. Chem. Rev. 2005, 105, 2253–2278. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Kumar, D.; de Visser, S.P.; Altun, A.; Thiel, W. Theoretical perspective on the structure and mechanism of cytochrome P450 enzymes. Chem. Rev. 2005, 105, 2279–2328. [Google Scholar] [CrossRef]
- Abu-Omar, M.M.; Loaiza, A.; Hontzeas, N. Reaction mechanisms of mononuclear non-heme iron oxygenases. Chem. Rev. 2005, 105, 2227–2252. [Google Scholar] [CrossRef]
- Poulos, T.L. Heme enzyme structure and function. Chem. Rev. 2014, 114, 3919–3962. [Google Scholar] [CrossRef]
- Guengerich, F.P.; Yoshimoto, F.K. Formation and cleavage of C–C bonds by enzymatic oxidation-reduction reactions. Chem. Rev. 2018, 118, 6573–6655. [Google Scholar] [CrossRef]
- Huang, X.; Groves, J.T. Oxygen activation and radical transformations in heme proteins and metalloporphyrins. Chem. Rev. 2018, 118, 2491–2553. [Google Scholar] [CrossRef]
- Beinert, H.; Holm, R.H.; Münck, E. Iron-sulfur clusters: Nature’s modular, multipurpose structures. Science 1997, 277, 653–659. [Google Scholar] [CrossRef]
- Noodleman, L.; Peng, C.Y.; Case, D.A.; Mouesca, J.-M. Orbital interactions, electron delocalization and spin coupling in iron-sulfur clusters. Coord. Chem. Rev. 1995, 144, 199–244. [Google Scholar] [CrossRef]
- Yamaguchi, K. The electronic structures of biradicals in the unrestricted Hartree-Fock approximation. Chem. Phys. Lett. 1975, 33, 330–335. [Google Scholar] [CrossRef]
- Takabe, T.; Yamaguchi, K. Electron-transfer biradical intermediates in ground-state reactions. Chem. Phys. Lett. 1976, 40, 347–352. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Ohta, K.; Yabushita, S.; Fueno, T. DODS natural orbital (NO) CI investigations of 1, 3-diradicals: CH2NHO, CH2OO, and CH2CH2O. J. Chem. Phys. 1978, 68, 4323–4325. [Google Scholar] [CrossRef]
- Slater, J.C.; Johnson, K.H. Self-consistent-field Xα cluster method for polyatomic molecules and solids. Phys. Rev. B 1972, 5, 844–853. [Google Scholar] [CrossRef]
- Noodleman, L.; Norman, J.G., Jr. The Xα valence bond theory of weak electronic coupling. Application to the low-lying states of Mo2Cl84−. J. Chem. Phys. 1979, 70, 4903–4906. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yabushita, S.; Fueno, T.; Kato, S.; Morokuma, K.; Iwata, S. Ab initio UHF and UHF NO CI approaches for quasi-degenerate systems: Methylene peroxide (CH2OO). Chem. Phys. Lett. 1980, 71, 563–568. [Google Scholar] [CrossRef]
- Roos, B.O.; Taylor, P.R.; Siegbahn, P.E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Wang, Q.; Zou, J.; Xu, E.; Pulay, P.; Li, S. Automatic construction of the initial orbitals for efficient generalized valence bond calculations of large systems. J. Chem. Theory Comput. 2019, 15, 141–153. [Google Scholar] [CrossRef]
- Pierloot, K.; de Kerpel, J.O.A.; Ryde, U.; Olsson, M.H.M.; Roos, B.O. Relation between the structure and spectroscopic properties of blue copper proteins. J. Am. Chem. Soc. 1998, 120, 13156–13166. [Google Scholar] [CrossRef]
- Vancoillie, S.; Zhao, H.; Tran, V.T.; Hendrickx, M.F.A.; Pierloot, K. Multiconfigurational second-order perturbation theory restricted active space (RASPT2) studies on mononuclear first-row transition-metal systems. J. Chem. Theory Comput. 2011, 7, 3961–3977. [Google Scholar] [CrossRef]
- Radoń, M.; Broclawik, E.; Pierloot, K. DFT and ab initio study of iron-oxo porphyrins: May they have a low-lying iron(V)-oxo electromer? J. Chem. Theory Comput. 2011, 7, 898–908. [Google Scholar] [CrossRef] [PubMed]
- Saitow, M.; Kurashige, Y.; Yanai, T. Fully internally contracted multireference configuration interaction theory using density matrix renormalization group: A reduced-scaling implementation derived by computer-aided tensor factorization. J. Chem. Theory Comput. 2015, 11, 5120–5131. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Karplus, M. Calculation of ground and excited state potential surfaces of conjugated molecules. I. Formulation and parametrization. J. Am. Chem. Soc. 1972, 94, 5612–5625. [Google Scholar] [CrossRef]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Karplus, M.; Petsko, G.A. Molecular dynamics simulations in biology. Nature 1990, 347, 631–639. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, D.; Thiel, W.; Shaik, S. QM/MM study of mechanisms for compound I formation in the catalytic cycle of cytochrome P450cam. J. Am. Chem. Soc. 2006, 128, 13204–13215. [Google Scholar] [CrossRef]
- Chen, H.; Song, J.; Lai, W.; Wu, W.; Shaik, S. Multiple low-lying states for compound I of P450cam and chloroperoxidase revealed from multireference ab initio QM/MM calculations. J. Chem. Theory Comput. 2010, 6, 940–953. [Google Scholar] [CrossRef]
- Čížek, J.; Paldus, J. Stability conditions for the solutions of the Hartree-Fock equations for atomic and molecular systems. Application to the pi-electron model of cyclic polyenes. J. Chem. Phys. 1967, 47, 3976–3985. [Google Scholar] [CrossRef]
- Fukutome, H. Spin density wave and charge transfer wave in long conjugated molecules. Prog. Theor. Phys. 1968, 40, 998–1012. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T.; Fukutome, H. A molecular-orbital theoretical classification of reactions of singlet ground-state molecules. Chem. Phys. Lett. 1973, 22, 461–465. [Google Scholar] [CrossRef]
- Sander, W. Carbonyl oxides: Zwitterions or diradicals? Angew. Chem. Int. Ed. 1990, 29, 344–354. [Google Scholar] [CrossRef]
- Bunnelle, W.H. Preparation, properties, and reactions of carbonyl oxides. Chem. Rev. 1991, 91, 335–362. [Google Scholar] [CrossRef]
- Jørgensen, K.A. Transition-metal-catalyzed epoxidations. Chem. Rev. 1989, 89, 431–458. [Google Scholar] [CrossRef]
- Sugimoto, H.; Oda, S.; Otsuki, T.; Hino, T.; Yoshida, T.; Shiro, Y. Crystal structure of human indoleamine 2,3-dioxygenase: Catalytic mechanism of O2 incorporation by a heme-containing dioxygenase. Proc. Natl. Acad. Sci. USA 2006, 103, 2611–2616. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Yamanaka, S.; Kawakami, T.; Nagao, H.; Yamaguchi, K. Effective exchange integrals for open-shell species by density functional methods. Chem. Phys. Lett. 1994, 231, 25–33. [Google Scholar] [CrossRef]
- Breslow, R. Antiaromaticity. Acc. Chem. Res. 1973, 6, 393–398. [Google Scholar] [CrossRef]
- Firestone, R.A. The diradical mechanism for 1,3-dipolar cycloadditions and related thermal pericyclic reactions. Tetrahedron 1977, 33, 3009–3039. [Google Scholar] [CrossRef]
- Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef]
- Kornblum, N.; Pink, P.; Yorka, K.V. The leaving group as a factor in the alkylation of ambident anions. J. Am. Chem. Soc. 1961, 83, 2779–2780. [Google Scholar] [CrossRef]
- Russell, G.A.; Norris, R.K.; Panek, E.J. Reactions of resonance stabilized anions. XXXII. Electron-transfer processes. XIII. Coupling reactions of tertiary carbanions with.alpha.-substituted nitro alkanes. J. Am. Chem. Soc. 1971, 93, 5839–5845. [Google Scholar] [CrossRef]
- Nagakura, S.; Tanaka, J. On the relation between the chemical reactivity and energy levels of the chemical reagent. J. Chem. Phys. 1954, 22, 563. [Google Scholar] [CrossRef]
- Hoffmann, R. Building bridges between inorganic and organic chemistry (Nobel lecture). Angew. Chem. Int. Ed. 1982, 21, 711–724. [Google Scholar] [CrossRef]
- Fukui, K. The role of frontier orbitals in chemical reactions (Nobel lecture). Angew. Chem. Int. Ed. 1982, 21, 801–809. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinhold, F. Natural bond orbital analysis of near-Hartree-Fock water dimer. J. Chem. Phys. 1983, 78, 4066–4073. [Google Scholar] [CrossRef]
- Coulson, C.A. Valence; Oxford Clarendon Press: London, UK, 1952. [Google Scholar]
- Yamaguchi, K.; Fueno, T. Correlation effects in singlet biradical species. Chem. Phys. 1977, 19, 35–42. [Google Scholar] [CrossRef]
- Paldus, J.; Čížek, J. Hartree-Fock stability and symmetry breaking: Oxygen doubly negative ion. Can. J. Chem. 1985, 63, 1803–1811. [Google Scholar] [CrossRef]
- Lykos, P.; Pratt, G.W. Discussion on the Hartree-Fock approximation. Rev. Mod. Phys. 1963, 35, 496–501. [Google Scholar] [CrossRef]
- Perdew, J.P.; Savin, A.; Burke, K. Escaping the symmetry dilemma through a pair-density interpretation of spin-density functional theory. Phys. Rev. A 1995, 51, 4531–4541. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Sun, J.; Nepal, N.K.; Kaplan, A.D. Interpretations of ground-state symmetry breaking and strong correlation in wavefunction and density functional theories. Proc. Natl. Acad. Sci. USA 2021, 118, e2017850118. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.; Bao, J.J.; Truhlar, D.G.; Gagliardi, L. Multiconfiguration pair-density functional theory. Annu. Rev. Phys. Chem. 2021, 72, 541–564. [Google Scholar] [CrossRef] [PubMed]
- Takatsuka, K.; Fueno, T.; Yamaguchi, K. Distribution of odd electrons in ground-state molecules. Theoret. Chim. Acta 1978, 48, 175–183. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Davidson, E.R. Distribution of effectively unpaired electrons. Chem. Phys. Lett. 2000, 330, 161–168. [Google Scholar] [CrossRef]
- Matsen, F.A.; Welsher, T.L. Spin-free quantum chemistry. XVI. Spin correlation. Int. J. Quant. Chem. 1975, 9, 171–188. [Google Scholar] [CrossRef]
- Marshall, W.; Lowde, R.D. Magnetic correlations and neutron scattering. Rep. Prog. Phys. 1968, 31, 705–775. [Google Scholar] [CrossRef]
- Shoji, M.; Koizumi, K.; Kitagawa, Y.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Theory of chemical bonds in metalloenzymes II: Hybrid-DFT studies in iron–sulfur clusters. Int. J. Quant. Chem. 2005, 105, 628–644. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Shepelevich, I.S. Information entropy in chemistry: An overview. Entropy 2021, 23, 1240. [Google Scholar] [CrossRef]
- Shoji, M.; Isobe, H.; Saito, T.; Yabushita, H.; Koizumi, K.; Kitagawa, Y.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Hagiwara, M.; et al. Theory of chemical bonds in metalloenzymes. VII. Hybrid-density functional theory studies on the electronic structures of P450. Int. J. Quant. Chem. 2008, 108, 631–650. [Google Scholar] [CrossRef]
- Shoji, M.; Isobe, H.; Saito, T.; Kitagawa, Y.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Theory of chemical bonds in metalloenzymes XI: Full geometry optimization and vibration analysis of porphyrin iron-oxo species. Int. J. Quant. Chem. 2008, 108, 2950–2965. [Google Scholar] [CrossRef]
- Isobe, H.; Nishihara, S.; Shoji, M.; Yamanaka, S.; Shimada, J.; Hagiwara, M.; Yamaguchi, K. Extended Hartree–Fock theory of chemical reactions. VIII. Hydroxylation reactions by P450. Int. J. Quant. Chem. 2008, 108, 2991–3009. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yamanaka, S.; Isobe, H.; Shoji, M.; Saito, T.; Kitagawa, Y.; Okumura, M.; Shimada, J. Theory of chemical bonds in metalloenzymes XIII: Singlet and triplet diradical mechanisms of hydroxylations with iron-oxo species and P450 are revisited. Int. J. Quant. Chem. 2009, 109, 3723–3744. [Google Scholar] [CrossRef]
- Isobe, H.; Yamaguchi, K.; Okumura, M.; Shimada, J. Role of perferryl–oxo oxidant in alkane hydroxylation catalyzed by cytochrome P450: A hybrid density functional study. J. Phys. Chem. B 2012, 116, 4713–4730. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Filatov, M.; Schröder, D.; Schwarz, H. Electronic structure makes a difference: Cytochrome P-450 mediated hydroxylations of hydrocarbons as a two-state reactivity paradigm. Chem. Eur. J. 1998, 4, 193–199. [Google Scholar] [CrossRef]
- Filatov, M.; Harris, N.; Shaik, S. On the “rebound” mechanism of alkane hydroxylation by cytochrome P450: Electronic structure of the intermediate and the electron transfer character in the rebound step. Angew. Chem. Int. Ed. 1999, 38, 3510–3512. [Google Scholar] [CrossRef]
- Filatov, M.; Harris, N.; Shaik, S. A theoretical study of electronic factors affecting hydroxylation by model ferryl complexes of cytochrome P-450 and horseradish peroxidase. J. Chem. Soc. Perkin Trans. 2 1999, 3, 399–410. [Google Scholar] [CrossRef]
- Ogliaro, F.; Harris, N.; Cohen, S.; Filatov, M.; de Visser, S.P.; Shaik, S. A model “rebound” mechanism of hydroxylation by cytochrome P450: Stepwise and effectively concerted pathways, and their reactivity patterns. J. Am. Chem. Soc. 2000, 122, 8977–8989. [Google Scholar] [CrossRef]
- Ogliaro, F.; Cohen, S.; de Visser, S.P.; Shaik, S. Medium polarization and hydrogen bonding effects on compound I of cytochrome P450: What kind of a radical is it really? J. Am. Chem. Soc. 2000, 122, 12892–12893. [Google Scholar] [CrossRef]
- Schröder, D.; Shaik, S.; Schwarz, H. Two-state reactivity as a new concept in organometallic chemistry. Acc. Chem. Res. 2000, 33, 139–145. [Google Scholar] [CrossRef]
- de Visser, S.P.; Ogliaro, F.; Harris, N.; Shaik, S. Multi-state epoxidation of ethene by cytochrome P450: A quantum chemical study. J. Am. Chem. Soc. 2001, 123, 3037–3047. [Google Scholar] [CrossRef]
- Ogliaro, F.; de Visser, S.P.; Cohen, S.; Sharma, P.K.; Shaik, S. Searching for the second oxidant in the catalytic cycle of cytochrome P450: A theoretical investigation of the iron(III)-hydroperoxo species and its epoxidation pathways. J. Am. Chem. Soc. 2002, 124, 2806–2817. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; de Visser, S.P.; Ogliaro, F.; Schwarz, H.; Schröder, D. Two-state reactivity mechanisms of hydroxylation and epoxidation by cytochrome P-450 revealed by theory. Curr. Opin. Chem. Biol. 2002, 6, 556–567. [Google Scholar] [CrossRef] [PubMed]
- De Visser, S.P.; Ogliaro, F.; Sharma, P.K.; Shaik, S. What factors affect the regioselectivity of oxidation by cytochrome P450? A DFT study of allylic hydroxylation and double bond epoxidation in a model reaction. J. Am. Chem. Soc. 2002, 124, 11809–11826. [Google Scholar] [CrossRef]
- Kumar, D.; de Visser, S.P.; Sharma, P.K.; Cohen, S.; Shaik, S. Radical clock substrates, their C−H hydroxylation mechanism by cytochrome P450, and other reactivity patterns: What does theory reveal about the clocks’ behavior? J. Am. Chem. Soc. 2004, 126, 1907–1920. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Hirao, H.; Que, L., Jr.; Shaik, S. Theoretical investigation of C−H hydroxylation by (N4Py)FeIV=O2+: An oxidant more powerful than P450? J. Am. Chem. Soc. 2005, 127, 8026–8027. [Google Scholar] [CrossRef]
- Dey, A.; Okamura, T.; Ueyama, N.; Hedman, B.; Hodgson, K.O.; Solomon, E.I. Sulfur K-edge XAS and DFT calculations on P450 model complexes: Effects of hydrogen bonding on electronic structure and redox potentials. J. Am. Chem. Soc. 2005, 127, 12046–12053. [Google Scholar] [CrossRef]
- Hirao, H.; Kumar, D.; Thiel, W.; Shaik, S. Two states and two more in the mechanisms of hydroxylation and epoxidation by cytochrome P450. J. Am. Chem. Soc. 2005, 127, 13007–13018. [Google Scholar] [CrossRef]
- Li, C.; Wu, W.; Kumar, D.; Shaik, S. Kinetic isotope effect is a sensitive probe of spin state reactivity in C−H hydroxylation of N,N-dimethylaniline by cytochrome P450. J. Am. Chem. Soc. 2006, 128, 394–395. [Google Scholar] [CrossRef]
- Chen, M.S.; White, M.C. A predictably selective aliphatic C–H oxidation reaction for complex molecule synthesis. Science 2007, 318, 783–787. [Google Scholar] [CrossRef]
- Wang, Y.; Kumar, D.; Yang, C.; Han, K.; Shaik, S. Theoretical study of N-demethylation of substituted N,N-dimethylanilines by cytochrome P450: The mechanistic significance of kinetic isotope effect profiles. J. Phys. Chem. B 2007, 111, 7700–7710. [Google Scholar] [CrossRef]
- Altun, A.; Shaik, S.; Thiel, W. What is the active species of cytochrome P450 during camphor hydroxylation? QM/MM studies of different electronic states of compound I and of reduced and oxidized iron−oxo intermediates. J. Am. Chem. Soc. 2007, 129, 8978–8987. [Google Scholar] [CrossRef] [PubMed]
- Hazan, C.; Kumar, D.; de Visser, S.P.; Shaik, S. A density functional study of the factors that influence the regioselectivity of toluene hydroxylation by cytochrome P450 enzymes. Eur. J. Inorg. Chem. 2007, 2007, 2966–2974. [Google Scholar] [CrossRef]
- Shaik, S.; Kumar, D.; de Visser, S.P. A valence bond modeling of trends in hydrogen abstraction barriers and transition states of hydroxylation reactions catalyzed by cytochrome P450 enzymes. J. Am. Chem. Soc. 2008, 130, 10128–10140. [Google Scholar] [CrossRef] [PubMed]
- Yoshizawa, K.; Shiota, Y.; Kagawa, Y. Energetics for the oxygen rebound mechanism of alkane hydroxylation by the iron-oxo species of cytochrome P450. Bull. Chem. Soc. Jpn. 2000, 73, 2669–2673. [Google Scholar] [CrossRef]
- Yoshizawa, K. Methane inversion on transition metal ions: A possible mechanism for stereochemical scrambling in metal-catalyzed alkane hydroxylations. J. Organomet. Chem. 2001, 635, 100–109. [Google Scholar] [CrossRef]
- Kamachi, T.; Yoshizawa, K. A theoretical study on the mechanism of camphor hydroxylation by compound I of cytochrome P450. J. Am. Chem. Soc. 2003, 125, 4652–4661. [Google Scholar] [CrossRef]
- Guallar, V.; Friesner, R.A. Cytochrome P450CAM enzymatic catalysis cycle: A quantum mechanics/molecular mechanics study. J. Am. Chem. Soc. 2004, 126, 8501–8508. [Google Scholar] [CrossRef]
- Jovanovic, T.; Farid, R.; Friesner, R.A.; McDermott, A.E. Thermal equilibrium of high- and low-spin forms of cytochrome P450 BM-3: Repositioning of the substrate? J. Am. Chem. Soc. 2005, 127, 13548–13552. [Google Scholar] [CrossRef]
- Ravindranathan, K.P.; Gallicchio, E.; Friesner, R.A.; McDermott, A.E.; Levy, R.M. Conformational equilibrium of cytochrome P450 BM-3 complexed with N-palmitoylglycine: A replica exchange molecular dynamics study. J. Am. Chem. Soc. 2006, 128, 5786–5791. [Google Scholar] [CrossRef]
- Bach, R.D.; Dmitrenko, O. The “somersault” mechanism for the P-450 hydroxylation of hydrocarbons. The intervention of transient inverted metastable hydroperoxides. J. Am. Chem. Soc. 2006, 128, 1474–1488. [Google Scholar] [CrossRef]
- McMillen, D.F.; Golden, D.M. Hydrocarbon bond dissociation energies. Annu. Rev. Phys. Chem. 1982, 33, 493–532. [Google Scholar] [CrossRef]
- Reinhard, F.G.C.; de Visser, S.P. Biodegradation of cosmetics products: A computational study of cytochrome P450 metabolism of phthalates. Inorganics 2017, 5, 77. [Google Scholar] [CrossRef]
- Guengerich, F.P. Mechanisms of cytochrome P450-catalyzed oxidations. ACS Catal. 2018, 8, 10964–10976. [Google Scholar] [CrossRef] [PubMed]
- Que, L., Jr.; Ho, R.Y.N. Dioxygen activation by enzymes with mononuclear non-heme iron active sites. Chem. Rev. 1996, 96, 2607–2624. [Google Scholar] [CrossRef] [PubMed]
- Solomon, E.I.; Brunold, T.C.; Davis, M.I.; Kemsley, J.N.; Lee, S.-K.; Lehnert, N.; Neese, F.; Skulan, J.; Yang, Y.-S.; Zhou, J. Geometric and electronic structure/function correlations in non-heme iron enzymes. Chem. Rev. 2000, 100, 235–350. [Google Scholar] [CrossRef]
- Bassan, A.; Blomberg, M.R.A.; Siegbahn, P.E.M.; Que, L., Jr. A density functional study of O−O bond cleavage for a biomimetic non-heme iron complex demonstrating an FeV-intermediate. J. Am. Chem. Soc. 2002, 124, 11056–11063. [Google Scholar] [CrossRef]
- Solomon, E.I.; Decker, A.; Lehnert, N. Non-heme iron enzymes: Contrasts to heme catalysis. Proc. Natl. Acad. Sci. USA 2003, 100, 3589–3594. [Google Scholar] [CrossRef]
- Rohde, J.-U.; In, J.-H.; Lim, M.H.; Brennessel, W.W.; Bukowski, M.R.; Stubna, A.; Munck, E.; Nam, W.; Que, L., Jr. Crystallographic and spectroscopic characterization of a nonheme Fe(IV)=O complex. Science 2003, 299, 1037–1039. [Google Scholar] [CrossRef]
- Price, J.C.; Barr, E.W.; Tirupati, B.; Bollinger, J.M.; Krebs, C. The first direct characterization of a high-valent iron intermediate in the reaction of an α-ketoglutarate-dependent dioxygenase: A high-spin Fe(IV) complex in taurine/α-ketoglutarate dioxygenase (TauD) from Escherichia coli. Biochemistry 2003, 42, 7497–7508. [Google Scholar] [CrossRef]
- Costas, M.; Mehn, M.P.; Jensen, M.P.; Que, L., Jr. Dioxygen activation at mononuclear nonheme iron active sites: Enzymes, models, and intermediates. Chem. Rev. 2004, 104, 939–986. [Google Scholar] [CrossRef]
- Hausinger, R.P. Fe(II)/α-ketoglutarate-dependent hydroxylases and related enzymes. Crit. Rev. Biochem. Mol. Biol. 2004, 39, 21–68. [Google Scholar] [CrossRef] [PubMed]
- Price, J.C.; Barr, E.W.; Hoffart, L.M.; Krebs, C.; Bollinger, J.M. Kinetic dissection of the catalytic mechanism of taurine:α-ketoglutarate dioxygenase (TauD) from Escherichia coli. Biochemistry 2005, 44, 8138–8147. [Google Scholar] [CrossRef] [PubMed]
- Hirao, H.; Kumar, D.; Que, L., Jr.; Shaik, S. Two-state reactivity in alkane hydroxylation by non-heme iron−oxo complexes. J. Am. Chem. Soc. 2006, 128, 8590–8606. [Google Scholar] [CrossRef] [PubMed]
- de Oliviera, F.T.; Chanda, A.; Banerjee, D.; Shan, X.; Mondal, S.; Que, L., Jr.; Bominaar, E.L.; Münck, E.; Collins, T.J. Chemical and spectroscopic evidence for an FeV-oxo complex. Science 2007, 315, 835–838. [Google Scholar] [CrossRef]
- Shaik, S.; Hirao, H.; Kumar, D. Reactivity of high-valent iron–oxo species in enzymes and synthetic reagents: A tale of many states. Acc. Chem. Res. 2007, 40, 532–542. [Google Scholar] [CrossRef]
- Krebs, C.; Fujimori, D.G.; Walsh, C.T.; Bollinger, J.M., Jr. Non-heme Fe(IV)–oxo intermediates. Acc. Chem. Res. 2007, 40, 484–492. [Google Scholar] [CrossRef]
- Nam, W. High-valent iron(IV)–oxo complexes of heme and non-heme ligands in oxygenation reactions. Acc. Chem. Res. 2007, 40, 522–531. [Google Scholar] [CrossRef]
- Bollinger, J.M., Jr.; Krebs, C. Enzymatic C-H activation by metal-superoxo intermediates. Curr. Opin. Chem. Biol. 2007, 11, 151–158. [Google Scholar] [CrossRef]
- Que, L., Jr. The road to non-heme oxoferryls and beyond. Acc. Chem. Res. 2007, 40, 493–500. [Google Scholar] [CrossRef]
- Hirao, H.; Que, L., Jr.; Nam, W.; Shaik, S. A two-state reactivity rationale for counterintuitive axial ligand effects on the C−H activation reactivity of nonheme FeIV=O oxidants. Chem. Eur. J. 2008, 14, 1740–1756. [Google Scholar] [CrossRef]
- Que, L., Jr.; Tolman, W.B. Biologically inspired oxidation catalysis. Nature 2008, 455, 333–340. [Google Scholar] [CrossRef] [PubMed]
- De Visser, S.P. Elucidating enzyme mechanism and intrinsic chemical properties of short-lived intermediates in the catalytic cycles of cysteine dioxygenase and taurine/α-ketoglutarate dioxygenase. Coord. Chem. Rev. 2009, 253, 754–768. [Google Scholar] [CrossRef]
- Prat, I.; Mathieson, J.S.; Güell, M.; Ribas, X.; Luis, J.M.; Cronin, L.; Costas, M. Observation of Fe(V)=O using variable-temperature mass spectrometry and its enzyme-like C–H and C=C oxidation reactions. Nat. Chem. 2011, 3, 788–793. [Google Scholar] [CrossRef] [PubMed]
- Hirao, H.; Li, F.; Que, L., Jr.; Morokuma, K. Theoretical study of the mechanism of oxoiron(IV) formation from H2O2 and a nonheme iron(II) complex: O–O cleavage involving proton-coupled electron transfer. Inorg. Chem. 2011, 50, 6637–6648. [Google Scholar] [CrossRef]
- Wilson, S.A.; Chen, J.; Hong, S.; Lee, Y.-M.; Clémancey, M.; Garcia-Serres, R.; Nomura, T.; Ogura, T.; Latour, J.-M.; Hedman, B.; et al. [FeIV=O(TBC)(CH3CN)]2+: Comparative reactivity of iron(IV)-oxo species with constrained equatorial cyclam ligation. J. Am. Chem. Soc. 2012, 134, 11791–11806. [Google Scholar] [CrossRef]
- De Visser, S.P.; Rohde, J.-U.; Lee, Y.-M.; Cho, J.; Nam, W. Intrinsic properties and reactivities of mononuclear nonheme iron–oxygen complexes bearing the tetramethylcyclam ligand. Coord. Chem. Rev. 2013, 257, 381–393. [Google Scholar] [CrossRef]
- Nam, W.; Lee, Y.-M.; Fukuzumi, S. Tuning reactivity and mechanism in oxidation reactions by mononuclear nonheme iron(IV)-oxo complexes. Acc. Chem. Res. 2014, 47, 1146–1154. [Google Scholar] [CrossRef]
- de Visser, S.P.; Quesne, M.G.; Martin, B.; Comba, P.; Ryde, U. Computational modelling of oxygenation processes in enzymes and biomimetic model complexes. Chem. Commun. 2014, 50, 262–282. [Google Scholar] [CrossRef]
- Puri, M.; Que, L., Jr. Toward the synthesis of more reactive S = 2 non-heme oxoiron(IV) complexes. Acc. Chem. Res. 2015, 48, 2443–2452. [Google Scholar] [CrossRef]
- Fan, R.; Serrano-Plana, J.; Oloo, W.N.; Draksharapu, A.; Delgado-Pinar, E.; Company, A.; Martin-Diaconescu, V.; Borrell, M.; Lloret-Fillol, J.; García-España, E.; et al. Spectroscopic and DFT characterization of a highly reactive nonheme FeV–oxo intermediate. J. Am. Chem. Soc. 2018, 140, 3916–3928. [Google Scholar] [CrossRef]
- Borrell, M.; Andris, E.; Navrátil, R.; Roithová, J.; Costas, M. Characterized cis-FeV(O)(OH) intermediate mimics enzymatic oxidations in the gas phase. Nat. Commun. 2019, 10, 901. [Google Scholar] [CrossRef]
- Shimoyama, Y.; Kojima, T. Metal–oxyl species and their possible roles in chemical oxidations. Inorg. Chem. 2019, 58, 9517–9542. [Google Scholar] [CrossRef] [PubMed]
- Oswald, V.F.; Lee, J.L.; Biswas, S.; Weitz, A.C.; Mittra, K.; Fan, R.; Li, J.; Zhao, J.; Hu, M.Y.; Alp, E.E.; et al. Effects of noncovalent interactions on high-spin Fe(IV)–oxido complexes. J. Am. Chem. Soc. 2020, 142, 11804–11817. [Google Scholar] [CrossRef] [PubMed]
- Andris, E.; Segers, K.; Mehara, J.; Rulíšek, L.; Roithová, J. Closed shell iron(IV) oxo complex with an Fe–O triple bond: Computational design, synthesis, and reactivity. Angew. Chem. Int. Ed. 2020, 59, 23137–23144. [Google Scholar] [CrossRef] [PubMed]
- Takahara, Y.; Yamaguchi, K.; Fueno, T. Potential energy curves for transition metal dimers and complexes calculated by the approximately projected unrestricted Hartree-Fock and Møller-Plesset perturbation (APUMP) methods. Chem. Phys. Lett. 1989, 158, 95–101. [Google Scholar] [CrossRef]
- Fiedler, A.; Schröder, D.; Shaik, S.; Schwarz, H. Electronic structures and gas-phase reactivities of cationic late-transition-metal oxides. J. Am. Chem. Soc. 1994, 116, 10734–10741. [Google Scholar] [CrossRef]
- Shaik, S.; Danovich, D.; Fiedler, A.; Schröder, D.; Schwarz, H. Two-state reactivity in organometallic gas-phase ion chemistry. Helv. Chim. Acta 1995, 78, 1393–1407. [Google Scholar] [CrossRef]
- Danovich, D.; Shaik, S. Spin−orbit coupling in the oxidative activation of H−H by FeO+. Selection rules and reactivity effects. J. Am. Chem. Soc. 1997, 119, 1773–1786. [Google Scholar] [CrossRef]
- Kim, C.; Chen, K.; Kim, J.; Que, L., Jr. Stereospecific alkane hydroxylation with H2O2 catalyzed by an iron(II)−tris(2-pyridylmethyl)amine complex. J. Am. Chem. Soc. 1997, 119, 5964–5965. [Google Scholar] [CrossRef]
- Filatov, M.; Shaik, S. Theoretical investigation of two-state-reactivity pathways of H−H activation by FeO+: Addition−elimination, “rebound”, and oxene-insertion mechanisms. J. Phys. Chem. A 1998, 102, 3835–3846. [Google Scholar] [CrossRef]
- Shoji, O.; Aiba, Y.; Watanabe, Y. Hoodwinking cytochrome P450BM3 into hydroxylating non-native substrates by exploiting its substrate misrecognition. Acc. Chem. Res. 2019, 52, 925–934. [Google Scholar] [CrossRef] [PubMed]
- Nesbet, R.K. Unrestricted Hartree–Fock then and now. Int. J. Quant. Chem. 2005, 102, 602–605. [Google Scholar] [CrossRef]
- Hanauske-Abel, H.M.; Günzler, V. A stereochemical concept for the catalytic mechanism of prolylhydroxylase: Applicability to classification and design of inhibitors. J. Theor. Biol. 1982, 94, 421–455. [Google Scholar] [CrossRef] [PubMed]
- Que, L., Jr. Metalloproteins with phenolate coordination. Coord. Chem. Rev. 1983, 50, 73–108. [Google Scholar] [CrossRef]
- Larson, V.A.; Battistella, B.; Ray, K.; Lehnert, N.; Nam, W. Iron and manganese oxo complexes, oxo wall and beyond. Nat. Rev. Chem. 2020, 4, 404–419. [Google Scholar] [CrossRef]
- Tripodi, G.L.; Roithová, J. Unmasking the iron–oxo bond of the [igand)Fe-OIAr]2+/+ complexes. J. Am. Soc. Mass Spectrom. 2022, 33, 1636–1643. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T.; Nasu, K. Ab initio MO calculations of effective exchange integrals between transition-metal ions via oxygen dianions: Nature of the copper-oxygen bonds and superconductivity. Jpn. J. Appl. Phys. 1987, 26, L1362–L1364. [Google Scholar] [CrossRef]
- Karlin, K.D.; Hayes, J.C.; Gultneh, Y.; Cruse, R.W.; McKown, J.W.; Hutchinson, J.P.; Zubieta, J. Copper-mediated hydroxylation of an arene: Model system for the action of copper monooxygenases. Structures of a binuclear copper(I) complex and its oxygenated product. J. Am. Chem. Soc. 1984, 106, 2121–2128. [Google Scholar] [CrossRef]
- Solomon, E.I.; Tuczek, F.; Root, D.E.; Brown, C.A. Spectroscopy of binuclear dioxygen complexes. Chem. Rev. 1994, 94, 827–856. [Google Scholar] [CrossRef]
- Wallar, B.J.; Lipscomb, J.D. Dioxygen activation by enzymes containing binuclear non-heme iron clusters. Chem. Rev. 1996, 96, 2625–2658. [Google Scholar] [CrossRef]
- Baik, M.-H.; Newcomb, M.; Friesner, R.A.; Lippard, S.J. Mechanistic studies on the hydroxylation of methane by methane monooxygenase. Chem. Rev. 2003, 103, 2385–2420. [Google Scholar] [CrossRef] [PubMed]
- Decker, A.; Clay, M.D.; Solomon, E.I. Spectroscopy and electronic structures of mono- and binuclear high-valent non-heme iron–oxo systems. J. Inorg. Biochem. 2006, 100, 697–706. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Shoji, M.; Isobe, H.; Yamanaka, S.; Kitagawa, Y.; Yamada, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Theory of chemical bonds in metalloenzymes. XIV. Correspondence between magnetic coupling mode and radical coupling mechanism in hydroxylations with methane monooxygenase and related species. Int. J. Quant. Chem. 2010, 110, 2955–2981. [Google Scholar] [CrossRef]
- Wachters, A.J. Gaussian basis set for molecular wavefunctions containing third-row atoms. J. Chem. Phys. 1970, 52, 1033–1036. [Google Scholar] [CrossRef]
- Bauschlicher, C.W., Jr.; Langhoff, S.R.; Partridge, H.; Barnes, L.A. Theoretical studies of the first- and second-row transition-metal methyls and their positive ions. J. Chem. Phys. 1989, 91, 2399–2411. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Cvetanović, R.J. Addition of atoms to olefins in the gas phase. In Advances in Photochemistry; Noyers, W.A., Jr., Hammond, G.S., Pitts, J.N., Jr., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1963; Volume 1, pp. 115–182. [Google Scholar]
- Fueno, T.; Takahara, Y.; Yamaguchi, K. Approximately projected UHF Møller-Plesset calculations of the potential energy profiles for the reaction of the triplet oxygen atom with ethylene. Chem. Phys. Lett. 1990, 167, 291–297. [Google Scholar] [CrossRef]
- Seger, S.T.; Rydberg, P.; Olsen, L. Mechanism of the N-hydroxylation of primary and secondary amines by cytochrome P450. Chem. Res. Toxicol. 2015, 28, 597–603. [Google Scholar] [CrossRef]
- Wasserman, H.H.; Murray, R.W. Singlet Oxygen; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Rodgers, M.A.J.; Powers, E.L. Oxygen and Oxy-Radicals in Chemistry and Biology; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Tinberg, C.E.; Lippard, S.J. Dioxygen activation in soluble methane monooxygenase. Acc. Chem. Res. 2011, 44, 280–288. [Google Scholar] [CrossRef]
- Banerjee, R.; Jones, J.C.; Lipscomb, J.D. Soluble methane monooxygenase. Annu. Rev. Biochem. 2019, 88, 409–431. [Google Scholar] [CrossRef] [PubMed]
- Fujisaki, H.; Ishizuka, T.; Kotani, H.; Shiota, Y.; Yoshizawa, K.; Kojima, T. Selective methane oxidation by molecular iron catalysts in aqueous medium. Nature 2023, 616, 476–481. [Google Scholar] [CrossRef]
- Arnold, F.H. Directed evolution: Bringing new chemistry to life. Angew. Chem. Int. Ed. 2018, 57, 4143–4148. [Google Scholar] [CrossRef]
- Ariyasu, S.; Yonemura, K.; Kasai, C.; Aiba, Y.; Onoda, H.; Shisaka, Y.; Sugimoto, H.; Tosha, T.; Kubo, M.; Kamachi, T.; et al. Catalytic oxidation of methane by wild-type cytochrome P450BM3 with chemically evolved decoy molecules. ACS Catal. 2023, 13, 8613–8623. [Google Scholar] [CrossRef]
- Bofill, J.M.; Pulay, P. The unrestricted natural orbital–complete active space (UNO–CAS) method: An inexpensive alternative to the complete active space–self-consistent-field (CAS–SCF) method. J. Chem. Phys. 1989, 90, 3637–3646. [Google Scholar] [CrossRef]
- Kawakami, T.; Miyagawa, K.; Sharma, S.; Saito, T.; Shoji, M.; Yamada, S.; Yamanaka, S.; Okumura, M.; Nakajima, T.; Yamaguchi, K. UNO DMRG CAS CI calculations of binuclear manganese complex Mn(IV)2O2(NHCHCO2)4: Scope and applicability of Heisenberg model. J. Comput. Chem. 2019, 40, 333–341. [Google Scholar] [CrossRef]
- Feldt, M.; Phung, Q.M.; Pierloot, K.; Mata, R.A.; Harvey, J.N. Limits of coupled-cluster calculations for non-heme iron complexes. J. Chem. Theory Comput. 2019, 15, 922–937. [Google Scholar] [CrossRef] [PubMed]
- Phung, Q.M.; Martín-Fernández, C.; Harvey, J.N.; Feldt, M. Ab initio calculations for spin-gaps of non-heme iron complexes. J. Chem. Theory Comput. 2019, 15, 4297–4304. [Google Scholar] [CrossRef] [PubMed]
- Feldt, M.; Martín-Fernández, C.; Harvey, J.N. Energetics of non-heme iron reactivity: Can ab initio calculations provide the right answer? Phys. Chem. Chem. Phys. 2020, 22, 23908–23919. [Google Scholar] [CrossRef]
- Veryazov, V.; Widmark, P.-O.; Serrano-Andrés, L.; Lindh, R.; Roos, B.O. 2MOLCAS as a development platform for quantum chemistry software. Int. J. Quant. Chem. 2004, 100, 626–635. [Google Scholar] [CrossRef]
- Chan, G.K.-L.; Sharma, S. The density matrix renormalization group in quantum chemistry. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [Google Scholar] [CrossRef] [PubMed]
- Schapiro, I.; Sivalingam, K.; Neese, F. Assessment of n-electron valence state perturbation theory for vertical excitation energies. J. Chem. Theory Comput. 2013, 9, 3567–3580. [Google Scholar] [CrossRef] [PubMed]
- Mahapatra, U.S.; Datta, B.; Bandyopadhyay, B.; Mukherjee, M. State-specific multi-reference coupled cluster formulations: Two paradigms. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Academic Press: New York, NY, USA, 1998; Volume 30, pp. 163–193. [Google Scholar]
- Liebermann, N.; Ghanem, K.; Alavi, A. Importance-sampling FCIQMC: Solving weak sign-problem systems. J. Chem. Phys. 2022, 157, 124111. [Google Scholar] [CrossRef] [PubMed]
- Montanaro, A. Quantum algorithms: An overview. NPJ Quantum Inf. 2016, 2, 15023. [Google Scholar] [CrossRef]
- Goings, J.J.; White, A.; Lee, J.; Tautermann, C.S.; Degroote, M.; Gidney, C.; Shiozaki, T.; Babbush, R.; Rubin, N.C. Reliably assessing the electronic structure of cytochrome P450 on today’s classical computers and tomorrow’s quantum computers. Proc. Acad. Natl. Sci. USA 2022, 119, e2203533119. [Google Scholar] [CrossRef]
- Romero, P.A.; Kuause, A.; Arnold, F.H. Navigating the protein fitness landscape with Gaussian processes. Proc. Acad. Natl. Sci. USA 2012, 110, E193–E201. [Google Scholar] [CrossRef]
- Coelho, P.S.; Brustad, E.M.; Kannan, A.; Arnold, F.H. Olefin cyclopropanation via carbene transfer catalyzed by engineered cytochrome P450 enzymes. Science 2012, 339, 307–310. [Google Scholar] [CrossRef]
- Chen, K.; Huang, X.; Kan, S.B.J.; Zhang, R.K.; Arnold, F.H. Enzymatic construction of highly strained carbocycles. Science 2018, 360, 71–75. [Google Scholar] [CrossRef]
- Nandy, A.; Zhu, J.; Janet, J.P.; Duan, C.; Getman, R.B.; Kulik, H.J. Machine learning accelerates the discovery of design rules and exceptions in stable metal–oxo intermediate formation. ACS Catal. 2019, 9, 8243–8255. [Google Scholar] [CrossRef]
- Ai, D.; Cai, H.; Wei, J.; Zhao, D.; Chen, Y.; Wang, L. DEEPCYPs: A deep learning platform for enhanced cytochrome P450 activity prediction. Front. Pharmacol. 2023, 14, 1099093. [Google Scholar] [CrossRef]
- Böselt, L.; Thürlemann, M.; Riniker, S. Machine learning in QM/MM molecular dynamics simulations of condensed-phase systems. J. Chem. Theory Comput. 2021, 17, 2641–2658. [Google Scholar] [CrossRef] [PubMed]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Zeguendry, A.; Jarir, Z.; Quafafou, M. Quantum machine learning: A review and case studies. Entropy 2023, 25, 287. [Google Scholar] [CrossRef] [PubMed]
| [M(X)OO] (a) | 2S + 1 | δ1 | δ2 | dσ | dπx | dπy | dπx* | dπy* | Fe (c) | O1 (b) | O2 (b) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cr(II)OO (c) | 3 | ↑ | 0 | ↑ | ↑ | ↑ | ↓ | ↓ | 1.86 | −0.37 | 0.51 |
| 7 | ↑ | 0 | ↑ | ↑ | ↑ | ↑ | ↑ | 1.86 | −0.43 | 0.57 | |
| L1Cr(II)OO (c,d) | 3 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↓ | ↓ | 1.40 | −0.51 | −0.26 |
| 7 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↑ | ↑ | 1.43 | −0.69 | −0.38 | |
| Fe(II)OO (c) | 3 | ↑ | ↑↓ | ↑ | ↑ | ↑ | ↓ | ↓ | 1.82 | −0.41 | 0.59 |
| 7 | ↑ | ↑↓ | ↑ | ↑ | ↑ | ↑ | ↑ | 1.84 | −0.44 | 0.60 | |
| L1Fe(II)OO (d) | 3 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↓ | ↓ | 1.24 | −0.35 | 0.08 |
| L12Fe(II)OO (d) | 3 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↓ | ↓ | 1.42 | −0.31 | −0.01 |
| L123Fe(II)OO (d) | 3 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↓ | ↑ | 1.44 | −0.31 | −0.07 |
| L13Fe(II)OO (d) | 3 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↓ | ↑↓ | 1.40 | −0.62 | −0.44 |
| L133Fe(II)OO (d) | 3 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↓ | ↓↓ | 1.41 | −0.56 | −0.51 |
| [M(X)O] (a) | 2S + 1 | δ1 | δ2 | σ | πx | πy | πx* | πy* | ΔE (b) | N.X. (c) |
|---|---|---|---|---|---|---|---|---|---|---|
| Cr(III)O | 4 | ↑ | ↑ | ↑↓ | ↑↓ | ↑↓ | 0 | ↑ | 0.0 | −0.19 |
| 6 | ↑ | ↑ | ↑↓ | ↑↓ | ↑ | ↑ | ↑ | 30.6 | −0.42 | |
| Cr(IV)O | 3 | ↑ | ↑ | ↑↓ | ↑↓ | ↑↓ | 0 | 0 | 0.0 | 0.35 |
| 7 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↑ | ↑ | 39.0 | 0.30 | |
| Cr(V)O | 2 | ↑ | 0 | ↑↓ | ↑↓ | ↑↓ | 0 | 0 | 0.0 | 0.96 |
| 6 | ↑ | 0 | ↑↓ | ↑ | ↑ | ↑ | ↑ | 70.0 | 0.65 | |
| Mn(III)O | 3 | ↑ | 0 | ↑↓ | ↑↓ | ↑↓ | 0 | ↑ | 0.0 | −0.04 |
| 5 | ↑ | 0 | ↑↓ | ↑ | ↑ | ↑ | ↑ | 44.0 | −0.04 | |
| Mn(IV)O | 2 | ↑ | 0 | ↑↓ | ↑↓ | ↑↓ | 0 | 0 | 0.0 | 0.33 |
| 4 | ↑ | 0 | ↑↓ | ↑↓ | ↑ | 0 | ↑ | 36.0 | 0.29 | |
| Mn(V)O | 3 | ↑ | ↑ | ↑↓ | ↑↓ | ↑↓ | 0 | 0 | 0.0 | 1.08 |
| 7 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↑ | ↑ | 64.4 | 1.06 | |
| Fe(II)O | 5 | ↑ | ↑ | ↑↓ | ↑↓ | ↑ | 0 | ↑ | 0.0 | −0.72 |
| 7 | ↑ | ↑ | ↑↓ | ↑ | ↑ | ↑ | ↑ | 12.9 | −0.62 | |
| Fe(III)O | 4 | ↑ | ↑ | ↑↓ | ↑↓ | ↑↓ | 0 | ↑ | 0.0 | −0.55 |
| 6 | ↑ | ↑ | ↑↓ | ↑↓ | ↑ | ↑ | ↑ | 18.4 | −0.59 | |
| Fe(IV)O | 3 | ↑↓ | 0 | ↑↓ | ↑↓ | ↑↓ | ↑ | ↑ | 0.0 | 0.55 |
| 1 | ↑↓ | 0 | ↑↓ | ↑↓ | ↑↓ | ↑ | ↓ | 26.7 | 0.35 |
| System | Spin State | UHF | UB3LYP | UBLYP | UCCSD(T) | Exp. | |||
|---|---|---|---|---|---|---|---|---|---|
| (1) (a) | (2) (b) | (1) (a) | (2) (b) | (1) (a) | (2) (b) | (2) (b) | |||
| CrO | 5Π | 1.90 | 1.86 | 1.66 | 1.62 | 1.65 | 1.62 | 1.66 | 1.615 |
| MnO | 6Σ+ | 1.88 | 1.87 | 1.66 | 1.63 | 1.67 | 1.64 | 1.69 | 1.648 |
| FeO | 5Δ | 1.84 | 1.83 | 1.63 | 1.61 | 1.64 | 1.62 | 1.65 | 1.619 |
| CoO | 5Δ | 1.85 | 1.84 | 1.64 | 1.63 | 1.66 | 1.65 | 1.64 | 1.631 |
| 4Σ− | 1.79 | 1.79 | 1.61 | 1.59 | 1.62 | 1.61 | 1.62 | ||
| NiO | 3Σ− | 1.80 | 1.81 | 1.63 | 1.63 | 1.65 | 1.65 | 1.64 | 1.631 |
| CuO | 2Π | 1.92 | 1.87 | 1.82 | 1.77 | 1.80 | 1.75 | 1.80 | 1.724 |
| System | Spin State | UHF | UB3LYP | UBLYP | UCCSD(T) | Exp. | |||
|---|---|---|---|---|---|---|---|---|---|
| (1) (a) | (2) (b) | (1) (a) | (2) (b) | (1) (a) | (2) (b) | (2) (b) | |||
| CrO | 5Π | 0.44 | 1.24 | 3.42 | 4.34 | 4.48 | 5.35 | 3.71 | 4.57 |
| 7Π | 0.12 | 0.98 | 2.26 | 2.92 | 2.72 | 3.29 | |||
| MnO | 6Σ+ | −0.28 | 1.13 | 2.50 | 4.09 | 3.64 | 5.26 | 2.94 | 3.83 |
| 4Π | −0.39 | 0.80 | 2.08 | 2.94 | 3.29 | 4.27 | |||
| 4Σ | −1.34 | 0.00 | 1.57 | 2.98 | 2.80 | 4.23 | |||
| 8Π | −0.03 | 1.43 | 1.32 | 2.58 | 1.70 | 2.94 | |||
| FeO | 5Δ | −0.39 | 1.05 | 2.89 | 4.38 | 4.07 | 5.34 | 3.21 | 4.17 |
| 3Φ | −0.19 | 1.03 | 2.47 | 3.36 | 3.72 | 4.38 | |||
| 5Σ+ | −0.90 | 0.48 | 2.96 | 3.91 | 4.21 | 4.82 | 2.96 | ||
| 7Σ+ | −1.31 | 0.31 | 1.99 | 3.40 | 2.96 | 4.08 | |||
| CoO | 4Δ | −1.05 | 0.35 | 3.00 | 4.07 | 4.36 | 5.43 | 2.92 | 3.94 |
| 4Σ− | −2.10 | 0.67 | 2.06 | 3.74 | 3.39 | 5.20 | 2.61 | ||
| 2Δ− | −0.43 | 0.78 | 2.35 | 3.44 | 3.70 | 4.85 | |||
| 6Δ | 1.46 | 0.18 | 1.83 | 3.21 | 2.94 | 4.36 | |||
| NiO | 3Σ− | −1.73 | −0.19 | 3.26 | 4.13 | 4.19 | 5.59 | 3.13 | 3.91 |
| 1Σ− | −2.76 | −1.37 | 2.82 | 3.72 | 3.81 | 5.24 | |||
| 5Σ | −0.54 | 0.37 | 1.72 | 2.69 | 2.46 | 4.01 | |||
| 5Δ | 0.00 | 0.01 | 1.62 | 2.28 | 2.17 | 3.30 | |||
| 5Φ | −0.47 | 0.91 | 1.47 | 2.30 | 1.41 | 2.94 | |||
| CuO | 2Π | 0.08 | 0.61 | 2.27 | 2.69 | 2.80 | 3.18 | 2.37 | 2.75 |
| 4Σ− | −0.26 | 0.02 | 0.74 | 0.93 | 1.50 | 1.57 | |||
| No. | Systems | δxy | σ | πzx | πzy | πzx* | πzy* | δx2−y2 | σ* | BO |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2Fe(V)=O | 2 | 2 | 2 | 2 | 1 | 0 | 0 | 0 | 2.5 |
| 2 | 2Fe(V)=O | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 1 | 2.5 |
| 3 | 4Fe(V)=O | 1 | 2 | 2 | 2 | 1 | 0 | 1 | 0 | 2.5 |
| 4 | 4Fe(V)=O | 1 | 2 | 2 | 2 | 0 | 0 | 1 | 1 | 2.5 |
| 5 | 4Fe(V)=O | 1 | 2 | 2 | 2 | 1 | 1 | 0 | 0 | 2.0 |
| 6 | 4Fe(V)=O | 1 | 2 | 2 | 2 | 1 | 0 | 0 | 1 | 2.0 |
| 7 | 2••Fe(V)–O•• | 2 | 2 | 1 + T | 1 + T | 1 − T | 1 − T | 0 | 1 | 0.5 + 2T |
| 8 | 2•Fe(V)–O• | 2 | 2 | 2 | 1 + T | 1 | 1 − T | 0 | 0 | 1.5 + T |
| 9 | 2•Fe(V)–O• | 2 | 2 | 2 | 1 + T | 1 | 0 | 0 | 1 − T | 1.5 + T |
| 10 | 2•Fe(V)–O• | 2 | 2 | 1 + T | 2 | 1 | 0 | 0 | 1 − T | 1.5 + T |
| 11 | 2•Fe(V)–O• | 2 | 1 + T | 2 | 2 | 1 | 0 | 0 | 1 − T | 1.5 + T |
| 12 | 4•Fe(V)–O• | 1 | 2 | 2 | 1 + T | 1 | 1 − T | 1 | 0 | 1.5 + T |
| 13 | 3Fe(IV)=O | 2 | 2 | 2 | 2 | 1 | 1 | 0 | 0 | 2.0 |
| 14 | 3Fe(IV)=O | 2 | 2 | 2 | 2 | 1 | 0 | 0 | 1 | 2.0 |
| 15 | 3Fe(IV)=O | 2 | 2 | 2 | 2 | 0 | 1 | 0 | 1 | 2.0 |
| 16 | 1Fe(IV)=O | 2 | 2 | 2 | 2 | 1 | 1 | 0 | 0 | 2.0 |
| 17 | 3•Fe(IV)=O• | 1 | 2 | 1 + T | 2 | 1 − T | 2 | 1 | 0 | 2.0 − T |
| 18 | 3•Fe(IV)=O• | 1 | 2 | 2 | 1 + T | 2 | 1 − T | 1 | 0 | 2.0 − T |
| 19 | 3•Fe(III)–O• | 2 | 2 | 2 | 1 + T | 1 | 1 − T | 0 | 1 | 1.0 + T |
| 20 | 3•Fe(III)–O• | 2 | 2 | 2 | 1 + T | 1 | 1 | 0 | 1 − T | 1.0 + T |
| 21 | 3•Fe(III)–O• | 2 | 1 + T | 2 | 2 | 1 | 1 | 0 | 1 − T | 1.0 + T |
| 22 | 5Fe(IV)=O | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 2.0 |
| 23 | 5Fe(IV)=O | 1 | 2 | 2 | 2 | 1 | 1 | 0 | 1 | 1.5 |
| 24 | 5•Fe(III)–O• | 1 | 2 | 2 | 1 + T | 1 | 1 − T | 1 | 1 | 1.0 + T |
| 25 | 5•Fe(III)–O• | 1 | 2 | 2 | 1 + T | 1 | 1 | 1 | 1 − T | 1.0 + T |
| 26 | 5•Fe(III)–O• | 1 | 1 + T | 2 | 2 | 1 | 1 | 1 | 1 − T | 1.0 + T |
| Model | Catalase | Peroxidase (a) | P450 | Model Complex | ||
|---|---|---|---|---|---|---|
| 1 | 2a | 2b | 3 | 4a | 4b | |
| Jcalc. | −29.3 | 9.1 | 59.9 | −20.4 | 40.66 | 29.57 |
| Jexp. | 6 (b) | −1.3 < Jexp (c) < 1.3 | −18 (d) | - | 21.5 | |
| System | Conf. | Jab (R(M–O), Angle) | |||
|---|---|---|---|---|---|
| CrIIIOCrIII | d3-d3 | −6204 (1.0) | −1987 (1.25) | −671 (1.5) | −377 (1.7) |
| XCrIIIOCrIIIX | d3-d3 | −187 (1.7) | −79 (1.8) | −10 (1.9) | |
| Mn0…Mn0 | d5-d5 | −32 (3.0) | −7 (3.5) | ||
| MnIIOMnII | d5-d5 | −3534 (1.0) | −156 (1.5) | 7 (2.0) | |
| XMnIIOMnIIX | d5-d5 | −24 (1.71) | |||
| XMnIIIOMnIIIX | d4-d4 | −60 (1.71) | |||
| FeIIIOFeIII | d5-d5 | −4913 (1.0) | −264 (1.5) | −71 (1.6) | 279 (1.8) |
| 326 (1.9) | |||||
| NiIIONiII | d8-d8 | −14754 (1.0) | −831 (1.5) | −525 (1.7) | |
| XNiIIONiIIX | d8-d8 | −174 (1.7) | |||
| CuIIOCuII | d9-d9 | −36453 (1.0) | −4621 (1.6) | −5433 (1.8) | |
| CuIIIOCuIII | d8-d8 | −19616 (1.0) | −5671 (1.6) | −5688 (1.8) | |
| CuII(OH)2CuII | d9-d9 | 554 (2.85, 97) | 207 (2.98, 103) | ||
| −175 (3.15, 110) | −170 (3.12, 110) | ||||
| H2CuII(OH)2NiIIH2 | d9-d8 | −24 (2.85, 95.6) | −170 (3.15, 110) | ||
| FeIII…FeIII | d5-d5 | −16 (2.70, 75) | |||
| FeIIIS2FeIII | d5-d5 | −926 (2.70, 75) | |||
| H2FeIIIS2FeIIIH2 | d5-d5 | −175 (2.70, 75) | |||
| Spin State | Fe | S | N | O | O(2) | ||
|---|---|---|---|---|---|---|---|
| A | S = 1/2 | Charge | 0.57 | 0.22 | −0.07 | 0.10 (H2O) | |
| Spin | 1.02 | 0.06 | 0.00 | 0.00 (H2O) | |||
| C | S = 2 | Charge | 1.06 | −0.15 | 0.12 | - | |
| Spin | 3.86 | 0.23 | 0.05 | - | |||
| S = 1 | Charge | 0.87 | −0.15 | −0.11 | - | ||
| Spin | 2.01 | 0.26 | −0.01 | - | |||
| S = 0 | Charge | 0.70 | 0.09 | −0.11 | - | ||
| Spin | 1.09 | −0.14 | −0.05 | - | |||
| D | S = 0 | Charge | 0.17 | −0.02 | 0.23 | −0.18 (O1) | −0.19 (O2) |
| Spin | 1.08 | 0.06 | 0.02 | −0.66 (O1) | −0.39 (O2) | ||
| E | S = 1/2 | Charge | 0.24 | −0.13 | 0.21 | −0.20 (O1) | −0.25 (O2) |
| Spin | 0.93 | −0.02 | −0.05 | 0.38 (O1) | 0.59 (O2) | ||
| F | S = 1/2 | Charge | 0.20 | 0.10 | 0.19 | −0.13 | |
| Spin | 1.19 | −0.81 | 0.04 | 0.91 |
| Entry | Orbital | Q | U | I | b | Y | B |
|---|---|---|---|---|---|---|---|
| D | σ | 0.220 | 0.048 | 0.970 | 0.975 | 0.000 | 0.999 |
| π | 0.966 | 0.934 | 0.207 | 0.257 | 0.517 | 0.482 | |
| E | σ (SP) | 0.192 | 0.037 | 0.977 | 0.981 | 0.000 | 0.999 |
| π | 0.898 | 0.806 | 0.380 | 0.441 | 0.261 | 0.738 | |
| F | π | 0.996 | 0.992 | 0.067 | 0.088 | 0.824 | 0.175 |
| No. | Type | Fe | O | Por | SR | H | C (a) | x | ΔE‡ (b) |
|---|---|---|---|---|---|---|---|---|---|
| II | 2CpdIb | 1.93 | −0.20 | −0.18 | −0.09 | 0.05 | −0.51 | 51.3 | 15.8 |
| IV | 2CpdIb | 1.86 | −0.07 | −0.19 | −0.09 | 0.03 | −0.54 | 52.2 | 20.3 |
| V | 2CpdIb | 1.87 | −0.05 | −0.22 | −0.17 | 0.02 | −0.45 | 52.4 | 17.7 |
| VI | 2CpdIb | 1.85 | −0.07 | −0.19 | −0.08 | 0.03 | −0.54 | 52.1 | 20.4 |
| VII | 2CpdIb | 1.82 | 0.12 | −0.31 | −0.24 | 0.01 | −0.40 | 48.6 | 15.2 |
| VIII | 2CpdIb | 1.82 | −0.03 | −0.22 | −0.12 | 0.02 | −0.47 | 51.7 | 17.3 |
| IX | 2CpdIb | 1.83 | 0.11 | −0.29 | −0.28 | 0.00 | −0.37 | 45.9 | 15.1 |
| X | 2CpdIb | 1.71 | 0.21 | −0.23 | −0.15 | −0.01 | −0.52 | 47.0 | 6.65 |
| XI | 2CpdIb | 1.81 | 0.11 | −0.30 | −0.22 | 0.01 | −0.41 | 53.3 | 14.8 |
| State | Fe | O | L (a) | CR3 | ΔE# * (b) | ΔE# ** (c) | |
|---|---|---|---|---|---|---|---|
| S = 0 | R | 0.54 | −0.51 | −0.03 | −0.00 | 0.0 (9.1) | 0.0 (8.5) |
| TS | 0.83 | −0.30 | −0.05 | −0.48 | 13 (14.0) | 9.4 (17.9) | |
| I | 0.90 | 0.09 | −0.06 | −0.94 | −1.3 (−1.8) | −8.3 (0.28) | |
| S = 1 | R | 1.11 | 0.96 | −0.07 | 0.00 | 0.0 (0.0) | 0.0 (0.0) |
| TS | 0.96 | 0.64 | −0.07 | 0.49 | 8.9 (8.9) | 12.5 (12.5) | |
| I | 0.91 | 0.22 | −0.06 | 0.93 | −1.5 (−1.5) | 0.87 (0.87) | |
| S = 2 | R | 2.98 | 0.73 | 0.29 | 0.00 | 0.0 (1.14) | 0.0 (0.43) |
| TS | 3.71 | 0.24 | 0.39 | −0.34 | 0.22 (1.36) | 7.1(7.5) | |
| I | 3.99 | 0.38 | 0.48 | −0.85 | 1.4 (−13.0) | 1.4 (−5.6) | |
| Methods | UB3LYP/Basis Set II | CASPT2 [15e, 16o] | RASPT2 [29e, 28o] |
|---|---|---|---|
| 4A2(a) | 0.0(0.0) | 0.0(0.0) | 0.0(0.0) |
| 2A2(a) | 0.1(0.4) | −1.4 (−0.6) | 0.0(0.4) |
| 2E (a) | 12.4 (12.7) | 1.6 (−3.4) | −1.7 (−6.5) |
| Δ (b) | –0.3 | 5.0 | 4.8 |
| Methods | UB3LYP | UB3LYP (a) | UB3LYP (a) | UB3LYP (b) | RAS [29e, 28o] |
|---|---|---|---|---|---|
| (ε = 0.0) | (ε = 5.7) | (ε = 78) | (average) | RAS2 [6 + SO] | |
| 4A2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2E | 12.4 | 5.7 | 7.9 | 6.8 (d) | 3.9 (d) (−1.7) |
| ΔΔ (c) | 0.0 | 6.7 | 4.5 | 5.6 (c) | 5.6 |
| ΔE(T-Q) (a) | ΔE#(Triplet) (b) | ΔE#(Quintet) (c) | C/non C (d) | ||
|---|---|---|---|---|---|
| Methods | Type (e) | ||||
| UB3LYP | XII | 3.1 | 21.7 | 10.4 | Cross |
| XIII | 7.6 | 14.3 | 3.5 | Cross | |
| UB3LYP-D3 | XII | 2.5 | 21.3 | 10.9 | Cross |
| XIII | 10.0 | 13.3 | 3.5 | Cross | |
| UB3LYP-UCCSD(T) | XII | 0.6 | 29.6 | 17.2 | Cross |
| UHF-UCCSD(T) | XII | −2.0 | 27.6 | 17.0 | Cross |
| DLPNO CCSD(T) | XII | −6.0 | 30.4 | 16.7 | Quintet |
| XIII | 1.8 | 25.4 | 8.8 | Quintet | |
| CASPT2 | XII | −3.3 | 31.7 | 15.7 | Triplet |
| XIII | 11.4 | 24.3 | 8.4 | Triplet | |
| CASPT2/CC | XII | 0.5 | 29.2 | 13.7 | Cross |
| XIII | 14.0 | 23.8 | 9.0 | Triplet | |
| CASSCF (12e,12o) | XII | −0.5 | 27.4 | 16.7 | Cross |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaguchi, K.; Isobe, H.; Shoji, M.; Kawakami, T.; Miyagawa, K. The Nature of the Chemical Bonds of High-Valent Transition–Metal Oxo (M=O) and Peroxo (MOO) Compounds: A Historical Perspective of the Metal Oxyl–Radical Character by the Classical to Quantum Computations. Molecules 2023, 28, 7119. https://doi.org/10.3390/molecules28207119
Yamaguchi K, Isobe H, Shoji M, Kawakami T, Miyagawa K. The Nature of the Chemical Bonds of High-Valent Transition–Metal Oxo (M=O) and Peroxo (MOO) Compounds: A Historical Perspective of the Metal Oxyl–Radical Character by the Classical to Quantum Computations. Molecules. 2023; 28(20):7119. https://doi.org/10.3390/molecules28207119
Chicago/Turabian StyleYamaguchi, Kizashi, Hiroshi Isobe, Mitsuo Shoji, Takashi Kawakami, and Koichi Miyagawa. 2023. "The Nature of the Chemical Bonds of High-Valent Transition–Metal Oxo (M=O) and Peroxo (MOO) Compounds: A Historical Perspective of the Metal Oxyl–Radical Character by the Classical to Quantum Computations" Molecules 28, no. 20: 7119. https://doi.org/10.3390/molecules28207119
APA StyleYamaguchi, K., Isobe, H., Shoji, M., Kawakami, T., & Miyagawa, K. (2023). The Nature of the Chemical Bonds of High-Valent Transition–Metal Oxo (M=O) and Peroxo (MOO) Compounds: A Historical Perspective of the Metal Oxyl–Radical Character by the Classical to Quantum Computations. Molecules, 28(20), 7119. https://doi.org/10.3390/molecules28207119