Next Article in Journal
Model Approach to Thermal Conductivity in Hybrid Graphene–Polymer Nanocomposites
Previous Article in Journal
Trans-(±)-TTPG-B Attenuates Cell Cycle Progression and Inhibits Cell Proliferation on Cholangiocarcinoma Cells
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 21
10.3390/molecules28217341
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Optoelectronic Evolution in Halogen-Doped Organic–Inorganic Halide Perovskites: A First-Principles Analysis

by
Cheng-Liang Xiao
,
Sicheng Liu
,
Xiao-Yan Liu
,
Yi-Ning Li
and
Peng Zhang
*
School of Space Science and Physics, Shandong University, Weihai 264209, China
*
Author to whom correspondence should be addressed.
Molecules 2023, 28(21), 7341; https://doi.org/10.3390/molecules28217341
Submission received: 11 October 2023 / Revised: 27 October 2023 / Accepted: 28 October 2023 / Published: 30 October 2023
(This article belongs to the Topic Advances in Computational Materials Sciences)
Browse Figures
Versions Notes

Abstract

:
Cl, Br, and I are elements in the halogen family, and are often used as dopants in semiconductors. When employed as dopants, these halogens can significantly modify the optoelectronic properties of materials. From the perspective of halogen doping, we have successfully achieved the stabilization of crystal structures in CH3NH3PbX3, CH3NH3PbI3−xClx, CH3NH3PbI3−xBrx, and CH3NH3PbBr3−xClx, which are organic–inorganic hybrid perovskites. Utilizing first-principles density functional theory calculations with the CASTEP module, we investigated the optoelectronic properties of these structures by simulations. According to the calculations, a smaller difference in electronegativity between different halogens in doped structures can result in smoother energy bands, especially in CH3NH3PbI3−xBrx and CH3NH3PbBr3−xClx. The PDOS of the Cl-3p orbitals undergoes a shift along the energy axis as a result of variances in electronegativity levels. The optoelectronic performance, carrier mobility, and structural stability of the CH3NH3PbBr3−xClx system are superior to other systems like CH3NH3PbX3. Among many materials considered, CH3NH3PbBr2Cl exhibits higher carrier mobility and a relatively narrower bandgap, making it a more suitable material for the absorption layer in solar cells. This study provides valuable insights into the methodology employed for the selection of specific types, quantities, and positions of halogens for further research on halogen doping.

Graphical Abstract

1. Introduction

In 2009, Kojima et al. introduced a novel dye-sensitized material known as the organic–inorganic hybrid perovskite CH3NH3PbX3 (X = I, Br). This material is cost-effective and can be produced at temperatures that are comparatively lower. At that time, solar cells exhibited a maximum power conversion efficiency (PCE) of merely 3.81%, and exhibited high instability. This marked the emergence of organic–inorganic hybrid perovskite solar cells [1]. In the past decade, there has been a remarkable advancement in the power conversion efficiency (PCE) of perovskite solar cells [2,3,4,5,6,7,8,9,10]. In the field of computational research on organic–inorganic hybrid perovskite structures, in 2013, Mosconi et al. conducted first-principles calculations on CH3NH3PbX3 (X = I, Br, Cl) and found a blue shift in the absorption spectrum as the halogen X changes from I to Br to Cl. Furthermore, they observed that the band structure trends in line with the experimentally obtained perovskite bandgap [11]. Additionally, they found that within the CH3NH3PbI2X (X = Cl, Br) system, Cl atoms exhibit a preference for occupying the top position of the PbI2X4 octahedron, while Br atoms have the capability to occupy either the top or equatorial positions. In 2014, Giacomo et al. employed first-principles calculation methods to examine the influence of organic cations on the optoelectronic properties of synthesized organic–inorganic hybrid perovskites CH3NH3PbX3 (X = I, Br, Cl). They found that in two-dimensional situations, organic molecules have a minimal impact on the band structure of perovskites, but they can alter the shape and orbital positions of the band edges [12]. In 2016, Pan et al. also used first-principles calculations to investigate the electronic structure and orbital compositions of the conduction and valence bands of CH3NH3PbX3 (X = I, Br, Cl). It was discovered that CH3NH3PbI3 can generate and transport more electrons compared to the other two structures [13]. As research has progressed, doping halogen elements has been verified as an effective strategy for modifying the physical properties of materials [14,15,16,17,18,19,20,21,22,23,24,25]. In 2019, Pramchu et al. applied density functional theory to investigate the impact of Cl and Br doping on the surface of CH3NH3PbI3 perovskites and their influence on structural stability. They found that Cl and Br dopants with higher binding energy to the surrounding atoms can prevent the deterioration of the perovskite. It was claimed that adding Cl/Br to MAPbI3 could overcome instability issues and enhance the efficiency of perovskite solar cells based on MAPbI3 [26]. While there have been numerous studies of halogens, the impact of the doping levels of I, Br, and Cl, and their impacts on the optoelectronic properties of organic–inorganic hybrid perovskite materials remain unknown. This includes adjusting the material’s bandgap through halogen doping, enhancing the material’s thermal stability and chemical stability, improving charge migration performance within the material, influencing crystal lattice parameters and structure, altering the material’s absorption characteristics at specific wavelengths, or addressing inherent defects within the material. Based on this, we conducted calculations on the established hybrid perovskite crystal structures, utilizing first-principles calculation methods to derive the electronic structure and optoelectronic properties of perovskite crystals in different systems. We evaluated the computed findings and investigated the regularities of the influence of halogen atom doping at different positions and in different quantities on the structure and properties of hybrid organic–inorganic perovskite materials. The observed results show that doping halogen elements with closer electronegativity and atomic radii can yield a more stable structure, resulting in a larger calculated curvature radius of the energy band. Due to the variation in doping elements, the PDOS of the Cl 3p orbitals experiences a shift along the energy axis, leading to a blue shift in the absorption spectrum and a consequent narrowing of the absorption range when doped with more electronegative elements.

2. Results and Discussion

2.1. Geometric Properties

In comparison with the original CH3NH3PbX3 structure, the introduction of halogen atoms as dopants in the organic–inorganic hybrid perovskite structures CH3NH3PbI3−xClx, CH3NH3PbI3−xBrx, and CH3NH3PbBr3−xClx causes distortions and a reduction in symmetry. This has a major impact on the bonding and properties of atoms within the crystal. Simulation calculations of the crystal structure play a crucial role in the study of such perovskites. The choice of an appropriate crystal structure model has a significant impact on the accuracy and efficiency of the calculations. Before calculating the original structure using first-principles methods, we tested the structural model’s convergence. The convergence test results are displayed in Figure 1. Considering both accuracy and efficiency, we selected a cutoff energy of 280 eV for the computations.
Using first-principles calculations, we optimized the crystal structures of all materials. For the optimization of CH3NH3PbI3, the largest change observed in bond length was 0.070 Å, while the largest change in bond angle was 2.307° compared with the characteristics of the same structures in reality. In addition, we examined the bond angles and lengths of the Pb-Cl-Pb bonds in the optimized structures of CH3NH3PbI3−xClx and CH3NH3PbBr3−xClx, as shown in Figure 2. It was found that the different doping elements had little effect on the bond length of Pb-Cl, but the Pb-Cl-Pb bond angle in the I-doped structure was smaller than that in the Br-doped structure at both octahedral vertices and equatorial positions. To analyze this phenomenon, we need to consider the differences between I and Br, including atomic size and steric repulsion, electronegativity, and electric field effects. When the I atom approaches the Pb-Cl-Pb structure, its large volume will cause steric repulsion with the nearby Pb-Cl-Pb, which will cause the Pb-Cl-Pb structure to deform to avoid contact with the I atom, resulting in the deviation of its bond angle from 180 degrees. In contrast, the steric repulsion caused by the smaller Br atom is relatively weak, so the Pb-Cl-Pb bond angle in the presence of Br is closer to 180 degrees. In addition, the electronegativity of Br is closer to that of Cl. The interaction between Br and the electron cloud of the Pb-Cl-Pb bond will cause the electrons in the bond to redistribute, resulting in a bond angle closer to 180 degrees. The lower electronegativity of I will not cause a significant electric field effect on the Pb-Cl-Pb bond angle, resulting in a deviation from 180 degrees. The closer the bond angle is to 180 degrees, the more balanced the repulsive force between the electrons on the central atom, and the more symmetrical the crystal structure becomes. This symmetry contributes to the excellent stability of the CH3NH3PbBr3−xClx structures.

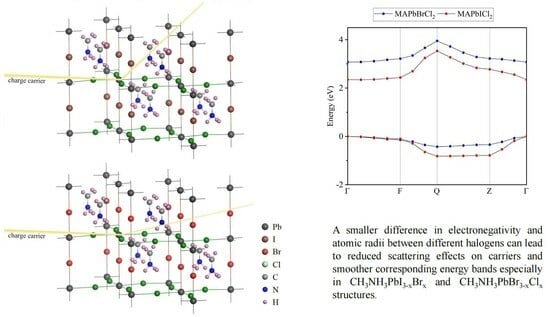
2.2. Electronic Properties

The condition for a material to generate electron-hole pairs is that the incident solar light ħω on the material surface is greater than the bandgap energy. Each pair can release the maximum energy that can be converted into short-circuit current, which is closely related to the bandgap width of the material. When the bandgap is greater, each electron-hole pair can release more energy. However, only a portion of ħω greater than the bandgap can be absorbed and excited into electron-hole pairs. In addition, although narrow bandgap materials are highly capable of generating electron-hole pairs, most of the energy is wasted due to the conversion of carriers and lattice collisions into heat energy, resulting in the very little energy that can be released by electron-hole pairs. Therefore, the value of the bandgap is an important parameter that affects the performance of solar cells. When the bandgap is roughly 2.5–2.6 eV, which is slightly less than the peak of the solar energy distribution, an optimal state is reached [27,28]. We calculated the band structures and bandgap widths of the optimized geometries of various systems using first-principles calculations, as presented in Table 1.
According to the calculation results mentioned above, doping with I, Br, and Cl will cause particular modifications to the structure’s lattice characteristics. Additionally, the bandgap of different structures will exhibit significant variations. The bandgap values of CH3NH3PbI3, CH3NH3PbI3−xClx, and CH3NH3PbCl3 structures were found to be 1.730 eV, 1.895 eV, 2.343 eV, and 3.183 eV, respectively. Compared with the reported values of 1.57 eV for CH3NH3PbI3 and 3.02 eV for CH3NH3PbCl3, the calculated values are slightly higher, with an error less than 10%, but they are in good agreement with the actual values, proving that our simulation calculations are instructive [29]. Based on the calculated bandgap size, CH3NH3PbBrCl2 and CH3NH3PbCl3 have a bandgap greater than 3 eV, making it difficult to excite, and are not suitable as light-absorbing materials for solar cells. The other systems are suitable as light-absorbing layers for solar cells. From the band structure diagram below, it can be seen that the Fermi level of all nine systems is located near the valence band, and the maximum value of the valence band top and the minimum value of the conduction band bottom appear at the same k point, indicating the characteristics of a direct bandgap p-type semiconductor, as shown in Figure 3 (with CH3NH3PbI3−xClx as an example). Compared with indirect bandgap semiconductors, direct bandgap semiconductors have higher photoelectric conversion efficiency because electrons can directly transition to the conduction band upon energy absorption.
In addition, the structures of the valence band maximum (VBM) and the conduction band minimum (CBM) of the nine systems were analyzed, as shown in Figure 4. From Figure 4a, it can be seen that the conduction band minimum and valence band maximum of CH3NH3PbCl3 and CH3NH3PbBr3 structures are flatter than those of other systems, making it easier for the conduction band minimum to accept electrons transitioning from the valence band, forming carriers. Therefore, this flat structure makes electron transition faster and more effective, making it more advantageous as a photoelectric conversion material. However, the energy band curve of the conduction band minimum in the CH3NH3PbI3−xClx system exhibits a significant curvature, which results in a higher degree of curvature; As a result, it is less likely to accept electrons transitioning from the valence band. In the Cl-doped system, the bandgap lies between CH3NH3PbCl3 and CH3NH3PbI3. The bandgap of CH3NH3PbI2Cl exhibits a high degree of similarity to that of CH3NH3PbI3. However, the valence band maximum and the conduction band minimum of CH3NH3PbI2Cl and CH3NH3PbICl2 structures are the sharpest, which makes them unsuitable for facilitating rapid electron transition.
From Figure 4b, we used the flattest CH3NH3PbBr3 as a reference point to assess the flatness of the CH3NH3PbI3−xBrx and CH3NH3PbBr3−xClx systems. We discovered that the flatness of these two systems is comparable to that of CH3NH3PbBr3.
In the periodic table, the atomic radii of Cl, Br, and I gradually increase. Because the atomic radius of Br is between Cl and I, the spatial changes it causes in the lattice are moderate. This means that the lattice distortion of CH3NH3PbI3−xBrx and CH3NH3PbBr3−xClx is smaller than that of CH3NH3PbI3−xClx. The reduced lattice distortion helps to obtain a more stable and smooth energy band. Different electronegativities will also affect the bond strength between halogen atoms and Pb atoms. The electronegativity difference between I and Br and between Br and Cl is smaller than that between I and Cl, making the chemical bonds formed by CH3NH3PbI3−xBrx and CH3NH3PbBr3−xClx closer to CH3NH3PbBr3, which helps to obtain a smoother energy band structure. In addition, the energy levels of different halogen p-orbitals vary, which will impact their overlap with the Pb 6s orbital. When the Pb 6s orbital hybridizes with the p orbitals of different halogens, the resulting hybrid orbitals will also be different, which will further affect the band structure. This will be further discussed in the analysis of PDOS later on.
When the electronegativity and atomic radius differences of halogen elements are smaller, the distribution of the electric field in the crystal structure is more uniform, and the arrangement of atoms is more closely packed and orderly. This reduces the scattering effects (including lattice scattering and impurity scattering) experienced by electrons during their motion. As a result, carriers experience less scattering, leading to a faster migration rate and, consequently, an increase in the material’s electrical conductivity. This is particularly crucial in semiconductors and photovoltaic materials. In solar cells, rapid carrier migration enhances the efficiency of the cells by reducing the probability of carrier recombination before reaching the electrodes, thereby minimizing energy loss.
By conducting first-principles calculations, it is feasible to attain the density of states (DOS) for each system, as well as the partial density of states (PDOS) of each atom within those systems. The valence band maximum is mainly contributed by the presence of halogens, while the contribution of Pb is predominantly responsible for the conduction band minimum. The valence band maximum is obtained from the halogen 5p state, while the conduction band minimum is obtained from the Pb 6s and 6p states. There is a relatively weak covalent interaction between Pb and halogens. The organic cation MA+ does not contribute to the valence band maximum or conduction band minimum, as shown in Figure 5a. In the systems CH3NH3PbI2Cl and CH3NH3PbICl2, the valence band maximum is jointly obtained from the I 5p state and the Cl 3p state, but the peak intensities of the two atoms are different. In CH3NH3PbI2Cl, the number of electrons on I is greater than that of Cl, indicating a stronger interaction between I and Pb compared to Cl. The opposite is true for CH3NH3PbICl2. This indicates that as the number of Cl substitutions increases, the contribution of Cl gradually strengthens, as shown in Figure 5b. We compare the total density of states diagrams of different systems, taking CH3NH3PbI3, CH3NH3PbCl3, and CH3NH3PbI3−xClx as examples. The density of states of the four systems exhibit similarities, and their molecular orbital bonding types are basically the same, with only minor variations in position. This indicates that the change of halogens has little effect on the overall orbital bonding, as shown in Figure 5c.
Now, let us focus on the issue of band smoothness that we discovered earlier. We take CH3NH3PbI2Cl and CH3NH3PbBr2Cl as examples and calculate the PDOS of their respective halogens, as shown in Figure 5d. Under the same doping amount, we found that the PDOS of the Cl 3p orbitals (two red lines) of CH3NH3PbI2Cl and CH3NH3PbBr2Cl shifted toward the Fermi level along the energy axis by 0.6 eV, due to the electronegativities of I, Br, and Cl being 2.66, 2.96, and 3.16, respectively. This difference in electronegativity implies that when adjacent to I, Cl undergoes a relatively small electric field effect. However, when adjacent to Br, it experiences an increased electric field effect, which results in different degrees of hybridization between the p orbitals of I and Br with the Cl 3p orbital, leading to a change in the energy level of the Cl 3p orbital. The difference in electronegativity also causes different extents of charge transfer from I or Br to Cl, which changes the charge state of the Cl atom, thereby affecting the energy level of its 3p orbital. In addition, the atomic radius of I is larger than that of Br, and the spatial relationship and interatomic distance in the two lattices are different. This difference also leads to a change in the strength of interaction between atoms.
In conclusion, due to the combined effects of electronegativity, atomic size, orbital overlap, hybridization, and charge transfer, the PDOS of the Cl 3p orbitals undergoes a shift along the energy axis.

2.3. Effective Masses

Carrier mobility, which is typically closely linked to the effective mass of electrons, is a crucial parameter for evaluating the potential for utilization in optoelectronic devices. In general, semiconductors with a small effective mass of carriers exhibit high carrier mobility. To analyze the mobility and transport properties of organic–inorganic halide perovskites, we focused on their effective masses. We observed that the effective mass of electrons in CH3NH3PbX3 (X = I, Br, Cl) decreases sequentially from X = I to Br to Cl, as presented in Table 2. However, no clear pattern was found in other doped structures, which is attributed to the chosen path and the distribution of doped elements. On our calculated G-F path, the effective mass of electrons and holes is influenced by factors such as the optimized lattice structure, atomic species, chemical bond energies, impurities and defects, and electron–electron interactions. However, by observing the table data, we can still see that the electron effective mass of CH3NH3PbBr2Cl is the smallest along the G-F path. This unique structure can effectively enhance carrier mobility, allowing electrons or holes to move faster and reduce scattering effects. The overall conductivity of the material will also increase. Meanwhile, it can increase the response speed of the carrier. When applied to optoelectronic devices, the carrier can respond faster to external stimuli.

2.4. Absorption Spectrum

The absorption spectrum reflects the material’s ability to absorb light in different wavelength bands. Therefore, analyzing the absorption spectrum can provide insights into the appropriate systems to be used as absorbing layers. By calculating the optical properties using first principles, we can obtain maps of the optical absorption coefficient for different systems. The optical absorption coefficient is directly proportional to the absorption spectrum. Therefore, the absorption spectrum can also be analyzed based on the absorption coefficient map. We analyzed the absorption spectra of CH3NH3PbI3−xClx and CH3NH3PbBr3−xClx and found that the absorption range of CH3NH3PbBr3−xClx is narrower and shifted toward shorter wavelengths, as shown in Figure 6. This is similar to the findings of Mosconi et al. in 2013, where the organic–inorganic hybrid perovskites CH3NH3PbX3 (X = I, Br, Cl) showed a blue shift in the absorption spectrum from X = I to Br to Cl [11]. This indicates that doping with more electronegative elements can also achieve a blue shift in the absorption spectrum. Br has higher electronegativity compared to I, leading to an increased bandgap width. A wider bandgap means that photons need higher energy, i.e., shorter wavelengths, to excite electrons from the valence band to the conduction band. Irregularities and defects in the crystal structure can broaden the absorption spectrum. CH3NH3PbBr3−xClx reduces such irregularities compared to CH3NH3PbI3−xClx, resulting in a narrower absorption spectrum. Although a narrower spectrum allows for higher resolution and sensitivity in the same spectral range, it can limit the efficiency of applications that require broad-spectrum absorption. In conclusion, it is important to determine its advantages and disadvantages based on specific applications and requirements. Further research can continue to modify the doping ratio of Br to achieve ideal performance.

3. Simulation Strategy

The CASTEP module is a first-principles calculation module based on density functional theory. Based on previous study findings and experimental comparisons, the GGA-PW91 exchange–correlation energy approximation method was selected, and the ultrasoft pseudopotential method was used for geometric optimization and calculation of relevant photoelectric properties [30,31,32,33,34,35,36,37]. Since the initial structure reported in the literature contains 48 atoms [38,39,40,41], as shown in Figure 7a, after convergence testing (detailed in the above text), considering the efficiency and accuracy of the calculations, a plane cutoff energy of 280 eV and a 3 × 3 × 2 k-point mesh were selected for the calculations. After obtaining the stable crystal structure of CH3NH3PbX3 (X = I, Br, Cl), different elements other than X were doped at the octahedral top and equatorial positions of the original perovskite CH3NH3PbX3 crystal structure, resulting in two different CH3NH3PbI3−xClx, CH3NH3PbI3−xBrx, and CH3NH3PbBr3−xClx structures, totaling six, as shown in Figure 7b,c (with CH3NH3PbI3−xClx as an example). The same method was used to calculate the geometric and electronic structures of these nine structures.
By utilizing the CASTEP program, geometric optimization and electronic structure calculations on the organic–inorganic hybrid perovskite can be conducted. This enables the acquisition of several parameters, such as band structure, density of states, charge distribution, and absorption spectra of the material’s crystal structure. Through the process of calculation, it is feasible to assess the impact of halogen atoms on the structure and properties of hybrid perovskites.

4. Conclusions

Based on our first-principles calculations, the crystal structure of CH3NH3PbBr3−xClx is more stable compared to CH3NH3PbI3−xClx. Additionally, the bandgap of CH3NH3PbBr2Cl makes it suitable as a light-absorbing material for solar cells. The Cl-3p orbital PDOS in CH3NH3PbI2Cl shifts toward the Fermi level along the energy axis compared to CH3NH3PbBr2Cl, due to doping with halogen elements that have similar electronegativity and atomic radii. The band structures of CH3NH3PbI3−xBrx and CH3NH3PbBr3−xClx are smoother, making them more receptive to transition electrons compared to CH3NH3PbI3−xClx. CH3NH3PbBr2Cl has the smallest effective mass of electrons along the G-F path, resulting in high carrier mobility, strong conductivity, fast response, and beneficial properties for optoelectronic devices. Doping with elements of higher electronegativity can also achieve a blue shift in the absorption spectrum.
The optoelectronic performance of the CH3NH3PbBr2Cl system is superior to other systems, with a more stable structure. Electrons in this system can undergo transitions more rapidly and efficiently, and the bandgap is close to the optimal value, making it suitable as a light-absorbing material for solar cell layers. Overall, we provide a thorough analysis of the band structure, density of states, partial density of states, and effective mass of different systems. We emphasize the importance of considering the electronegativity of elements in predicting and explaining doping effects. Our investigations also reveal the consistent changes in optoelectronic performance that result from doping different elements. These provide important insights for further refinement of doping research and serve as a valuable guide for solar cell design.

Author Contributions

C.-L.X. is mainly responsible for model construction and article writing; S.L. assisted structural modeling and data processing; X.-Y.L. and Y.-N.L. helped to analyze the data and discuss the results; P.Z. conducted simulations, data analysis, and edited the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

We are grateful to the project ZR2022MA017 supported by Shandong Provincial Natural Science for financial support.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are available from the authors.

Acknowledgments

The numerical calculations were performed on the supercomputing system at the Supercomputing Center, Shandong University, Weihai.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
  2. Wu, T.H.; Qin, Z.Z.; Wang, Y.B.; Wu, Y.Z.; Chen, W.; Zhang, S.F.; Cai, M.L.; Dai, S.Y.; Zhang, J.; Liu, J.; et al. The Main Progress of Perovskite Solar Cells in 2020–2021. Nano-Micro Lett. 2021, 13, 152. [Google Scholar] [CrossRef] [PubMed]
  3. Deng, L.-L.; Xie, S.-Y.; Huang, R.-B.; Zheng, L.-S. Research Progress in Perovskite Solar Cell Materials and Devices. J. Xiamen Univ. Nat. Sci. 2015, 54, 619–629. [Google Scholar]
  4. Koscher, B.A.; Swabeck, J.K.; Bronstein, N.D.; Alivisatos, A.P. Essentially Trap-Free CsPbBr3 Colloidal Nanocrystals by Postsynthetic Thiocyanate Surface Treatment. J. Am. Chem. Soc. 2017, 139, 6566–6569. [Google Scholar] [CrossRef]
  5. Wang, Y.; Liu, X.M.; Zhang, T.Y.; Wang, X.T.; Kan, M.; Shi, J.L.; Zhao, Y.X. The Role of Dimethylammonium Iodide in CsPbI3 Perovskite Fabrication: Additive or Dopant? Angew. Chem.-Int. Ed. 2019, 58, 16691–16696. [Google Scholar] [CrossRef]
  6. Wei, H.T.; DeSantis, D.; Wei, W.; Deng, Y.H.; Guo, D.Y.; Savenije, T.J.; Cao, L.; Huang, J.S. Dopant compensation in alloyed CH3NH3PbBr3−xClx perovskite single crystals for gamma-ray spectroscopy. Nat. Mater. 2017, 16, 826–833. [Google Scholar] [CrossRef] [PubMed]
  7. Zhang, H.L.; Xu, H.Y.; Ji, X.; Liang, J.K.; Yu, Q.F. Progress toward Applications of Perovskite Solar Cells. Energy Fuels 2020, 34, 6624–6633. [Google Scholar] [CrossRef]
  8. Zhang, W.; Peng, X.; Feng, X. Recent progress of perovskite solar cells. Electron. Compon. Mater. 2014, 33, 7–11. [Google Scholar] [CrossRef]
  9. Alla, M.; Manjunath, V.; Chawki, N.; Singh, D.; Yadav, S.C.; Rouchdi, M.; Boubker, F. Optimized CH3NH3PbI3−XClX based perovskite solar cell with theoretical efficiency exceeding 30%. Opt. Mater. 2022, 124, 112044. [Google Scholar] [CrossRef]
  10. Ayad, M.; Fathi, M.; Mellit, A. Study and performance analysis of Perovskite solar cell structure based on organic and inorganic thin films. Optik 2021, 233, 166619. [Google Scholar] [CrossRef]
  11. Mosconi, E.; Amat, A.; Nazeeruddin, M.K.; Grätzel, M.; De Angelis, F. First-Principles Modeling of Mixed Halide Organometal Perovskites for Photovoltaic Applications. J. Phys. Chem. C 2013, 117, 13902–13913. [Google Scholar] [CrossRef]
  12. Giorgi, G.; Fujisawa, J.I.; Segawa, H.; Yamashita, K. Cation Role in Structural and Electronic Properties of 3D Organic-Inorganic Halide Perovskites: A DFT Analysis. J. Phys. Chem. C 2014, 118, 12176–12183. [Google Scholar] [CrossRef]
  13. Pan, Y.Y.; Su, Y.H.; Hsu, C.H.; Huang, L.W.; Kaun, C.C. The electronic structure of organic-inorganic hybrid perovskite solar cell: A first-principles analysis. Comput. Mater. Sci. 2016, 117, 573–578. [Google Scholar] [CrossRef]
  14. Zheng, F.; Takenaka, H.; Wang, F.; Koocher, N.Z.; Rappe, A.M. First-Principles Calculation of the Bulk Photovoltaic Effect in CH3NH3PbI3 and CH3NH3PbI3–xClx. J. Phys. Chem. Lett. 2015, 6, 31–37. [Google Scholar] [CrossRef]
  15. Wang, S.; Xiao, W.-b.; Wang, F. Structural, electronic, and optical properties of cubic formamidinium lead iodide perovskite: A first-principles investigation. RSC Adv. 2020, 10, 32364–32369. [Google Scholar] [CrossRef]
  16. Liu, S.; Zheng, F.; Koocher, N.Z.; Takenaka, H.; Wang, F.; Rappe, A.M. Ferroelectric Domain Wall Induced Band Gap Reduction and Charge Separation in Organometal Halide Perovskites. J. Phys. Chem. Lett. 2015, 6, 693–699. [Google Scholar] [CrossRef] [PubMed]
  17. Filippetti, A.; Delugas, P.; Mattoni, A. Radiative Recombination and Photoconversion of Methylammonium Lead Iodide Perovskite by First Principles: Properties of an Inorganic Semiconductor within a Hybrid Body. J. Phys. Chem. C 2014, 118, 24843–24853. [Google Scholar] [CrossRef]
  18. Quarti, C.; Mosconi, E.; Umari, P.; De Angelis, F. Chlorine Incorporation in the CH3NH3PbI3 Perovskite: Small Concentration, Big Effect. Inorg. Chem. 2017, 56, 74–83. [Google Scholar] [CrossRef]
  19. Yan, W.-L.; Lu, G.-H.; Liu, F. Effect of Chlorine Substitution on Lattice Distortion and Ferroelectricity of CH3NH3PbI3. J. Phys. Chem. C 2016, 120, 17972–17977. [Google Scholar] [CrossRef]
  20. Long, R.; Prezhdo, O.V. Dopants Control Electron–Hole Recombination at Perovskite–TiO2 Interfaces: Ab Initio Time-Domain Study. ACS Nano 2015, 9, 11143–11155. [Google Scholar] [CrossRef]
  21. Xu, F.; Zhang, T.; Li, G.; Zhao, Y. Synergetic Effect of Chloride Doping and CH3NH3PbCl3 on CH3NH3PbI3−xClx Perovskite-Based Solar Cells. ChemSusChem 2017, 10, 2365–2369. [Google Scholar] [CrossRef] [PubMed]
  22. Caputo, M.; Cefarin, N.; Radivo, A.; Demitri, N.; Gigli, L.; Plaisier, J.R.; Panighel, M.; Di Santo, G.; Moretti, S.; Giglia, A.; et al. Electronic structure of MAPbI3 and MAPbCl3: Importance of band alignment. Sci. Rep. 2019, 9, 15159. [Google Scholar] [CrossRef] [PubMed]
  23. Petrovai, I.; Todor-Boer, O.; David, L.; Botiz, I. Growth of Hybrid Perovskite Crystals from CH3NH3PbI3−xClx Solutions Subjected to Constant Solvent Evaporation Rates. Materials 2023, 16, 2625. [Google Scholar] [CrossRef] [PubMed]
  24. Yerezhep, D.; Omarova, Z.; Aldiyarov, A.; Shinbayeva, A.; Tokmoldin, N. IR Spectroscopic Degradation Study of Thin Organometal Halide Perovskite Films. Molecules 2023, 28, 1288. [Google Scholar] [CrossRef]
  25. Siddique, Z.; Payne, J.L.; Irvine, J.T.S.; Jagadamma, L.K.; Akhter, Z.; Samuel, I.D.W.; Iqbal, A. Effect of halide-mixing on tolerance factor and charge-carrier dynamics in (CH3NH3PbBr3−xClx) perovskites powders. J. Mater. Sci.-Mater. Electron. 2020, 31, 19415–19428. [Google Scholar] [CrossRef]
  26. Pramchu, S.; Cheiwchanchamnangij, T.; Laosiritaworn, Y.; Jaroenjittichai, A.P. Enhancing surface stabilization of CH3NH3PbI3 perovskite by Cl and Br doping: First-principles study. J. Appl. Phys. 2019, 125, 115302. [Google Scholar] [CrossRef]
  27. Keremane, K.S.; Rao, R.; Adhikari, A.V. Simple 3,6-disubstituted Carbazoles as Potential Hole Transport Materials: Photophysical, Electrochemical and Theoretical Studies. Photochem. Photobiol. 2021, 97, 289–300. [Google Scholar] [CrossRef]
  28. Somsongkul, V.; Lang, F.; Jeong, A.R.; Rusu, M.; Arunchaiya, M.; Dittrich, T. Hole blocking PbI2/CH3NH3PbI3 interface. KU Knowl. Repos. 2014, 8, 763–766. [Google Scholar]
  29. Cao, D.Y.H.; Guo, P.J.; Mannodi-Kanakkithodi, A.; Wiederrecht, G.P.; Gosztola, D.J.; Jeon, N.; Schaller, R.D.; Chan, M.K.Y.; Martinson, A.B.F. Charge Transfer Dynamics of Phase-Segregated Halide Perovskites: CH3NH3PbCl3 and CH3NH3PbI3 or (C4H9NH3)2(CH3NH3)n−1PbnI3n+1 Mixtures. ACS Appl. Mater. Interfaces 2019, 11, 9583–9593. [Google Scholar] [CrossRef]
  30. Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
  31. Laasonen, K.; Pasquarello, A.; Car, R.; Lee, C.; Vanderblit, D. Car-parrinello molecular-dynamics with vanderbilt ultrasoft pseudopotentials. Phys. Rev. B 1993, 47, 10142–10153. [Google Scholar] [CrossRef] [PubMed]
  32. Garrity, K.F.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Pseudopotentials for high-throughput DFT calculations. Comput. Mater. Sci. 2014, 81, 446–452. [Google Scholar] [CrossRef]
  33. Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Fur Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
  34. Feng, J.; Xiao, B. Effective Masses and Electronic and Optical Properties of Nontoxic MASnX3 (X = Cl, Br, and I) Perovskite Structures as Solar Cell Absorber: A Theoretical Study Using HSE06. J. Phys. Chem. C 2014, 118, 19655–19660. [Google Scholar] [CrossRef]
  35. Han, X.; Amrane, N.; Qamhieh, N.; Zhang, Z.; Benkraouda, M. Optoelectronic functionality and photovoltaic performance of Sr-doped tetragonal CH3NH3PbI3: A first-principles study. Phys. B Condens. Matter 2023, 649, 414453. [Google Scholar] [CrossRef]
  36. Shi, J.; Yun, S. First-Principles DFT Calculations for Perovskite Solar Cells. In Counter Electrodes for Dye-Sensitized and Perovskite Solar Cells; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 487–509. [Google Scholar]
  37. Peng, C.; Chen, J.; Wang, H.; Hu, P. First-Principles Insight into the Degradation Mechanism of CH3NH3PbI3 Perovskite: Light-Induced Defect Formation and Water Dissociation. J. Phys. Chem. C 2018, 122, 27340–27349. [Google Scholar] [CrossRef]
  38. Lin, Q.Q.; Armin, A.; Nagiri, R.C.R.; Burn, P.L.; Meredith, P. Electro-optics of perovskite solar cells. Nat. Photonics 2015, 9, 106–112. [Google Scholar] [CrossRef]
  39. Arakcheeva, A.; Chernyshov, D.; Spina, M.; Forró, L.; Horváth, E. CH3NH3PbI3: Precise structural consequences of water absorption at ambient conditions. Acta Crystallogr. Sect. B-Struct. Sci. Cryst. Eng. Mater. 2016, 72, 716–722. [Google Scholar] [CrossRef]
  40. Stoumpos, C.C.; Malliakas, C.D.; Kanatzidis, M.G. Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties. Inorg. Chem. 2013, 52, 9019–9038. [Google Scholar] [CrossRef]
  41. Jaffe, A.; Lin, Y.; Beavers, C.M.; Voss, J.; Mao, W.L.; Karunadasa, H.I. High-Pressure Single-Crystal Structures of 3D Lead-Halide Hybrid Perovskites and Pressure Effects on their Electronic and Optical Properties. ACS Cent. Sci. 2016, 2, 201–209. [Google Scholar] [CrossRef]
Molecules 28 07341 g001
Figure 1. Test results for convergence of structural models.
Figure 1. Test results for convergence of structural models.
Molecules 28 07341 g001
Molecules 28 07341 g002
Figure 2. Optimized geometric structures of CH3NH3PbI3−xClx and CH3NH3PbBr3−xClx perovskites. (a,b) are the top views of CH3NH3PbBrCl2 and CH3NH3PbICl2, respectively. (c,d) are the side views of CH3NH3PbBr2Cl and CH3NH3PbI2Cl, respectively. Numbers in all figures represent the bond lengths and bond angles, respectively.
Figure 2. Optimized geometric structures of CH3NH3PbI3−xClx and CH3NH3PbBr3−xClx perovskites. (a,b) are the top views of CH3NH3PbBrCl2 and CH3NH3PbICl2, respectively. (c,d) are the side views of CH3NH3PbBr2Cl and CH3NH3PbI2Cl, respectively. Numbers in all figures represent the bond lengths and bond angles, respectively.
Molecules 28 07341 g002
Molecules 28 07341 g003
Figure 3. Band structure of: (a) CH3NH3PbI2Cl, (b) CH3NH3PbICl2 perovskites.
Figure 3. Band structure of: (a) CH3NH3PbI2Cl, (b) CH3NH3PbICl2 perovskites.
Molecules 28 07341 g003
Molecules 28 07341 g004
Figure 4. The valence band maximum and conduction band minimum of: (a) CH3NH3PbX3 (X = I, Br, Cl) and CH3NH3PbI3−xClx, (b) CH3NH3PbBr3, CH3NH3PbI3−xBrx and CH3NH3PbBr3−xClx perovskites.
Figure 4. The valence band maximum and conduction band minimum of: (a) CH3NH3PbX3 (X = I, Br, Cl) and CH3NH3PbI3−xClx, (b) CH3NH3PbBr3, CH3NH3PbI3−xBrx and CH3NH3PbBr3−xClx perovskites.
Molecules 28 07341 g004
Molecules 28 07341 g005
Figure 5. (a) DOS and PDOS of CH3NH3PbI3 perovskites. (b) PDOS of the Cl 3p orbitals and the I 5p orbitals of CH3NH3PbI3−xClx perovskites. (c) DOS of CH3NH3PbI3, CH3NH3PbCl3 and CH3NH3PbI3−xClx perovskites. (d) PDOS of CH3NH3PbI2Cl and CH3NH3PbBr2Cl perovskites.
Figure 5. (a) DOS and PDOS of CH3NH3PbI3 perovskites. (b) PDOS of the Cl 3p orbitals and the I 5p orbitals of CH3NH3PbI3−xClx perovskites. (c) DOS of CH3NH3PbI3, CH3NH3PbCl3 and CH3NH3PbI3−xClx perovskites. (d) PDOS of CH3NH3PbI2Cl and CH3NH3PbBr2Cl perovskites.
Molecules 28 07341 g005
Molecules 28 07341 g006
Figure 6. Absorption coefficient graphs of: (a) CH3NH3PbBr2Cl and CH3NH3PbI2Cl structures, (b) CH3NH3PbBrCl2 and CH3NH3PbICl2 structures.
Figure 6. Absorption coefficient graphs of: (a) CH3NH3PbBr2Cl and CH3NH3PbI2Cl structures, (b) CH3NH3PbBrCl2 and CH3NH3PbICl2 structures.
Molecules 28 07341 g006
Molecules 28 07341 g007
Figure 7. The geometric structures of: (a) CH3NH3PbI3, (b) CH3NH3PbI2Cl doped at the octahedral top, (c) CH3NH3PbICl2 doped at the equatorial position.
Figure 7. The geometric structures of: (a) CH3NH3PbI3, (b) CH3NH3PbI2Cl doped at the octahedral top, (c) CH3NH3PbICl2 doped at the equatorial position.
Molecules 28 07341 g007
Table 1. Geometrically optimized bandgap for different structure types. (MA = CH3NH3).
Table 1. Geometrically optimized bandgap for different structure types. (MA = CH3NH3).
StructureBandgap (eV)StructureBandgap (eV)StructureBandgap (eV)
MAPbI31.730MAPbBr32.544MAPbCl33.183
MAPbI2Cl1.895MAPbBr2Cl2.578MAPbI2Br1.888
MAPbICl22.343MAPbBrCl23.076MAPbIBr22.093
Table 2. Effective carrier masses in different structure types of organic–inorganic halide perovskites (MA = CH3NH3).
Table 2. Effective carrier masses in different structure types of organic–inorganic halide perovskites (MA = CH3NH3).
Structure TypememhStructure Typememh
MAPbI30.643 m0−0.514 m0MAPbI2Cl0.265 m0−0.207 m0
MAPbBr30.445 m0−0.866 m0MAPbICl21.692 m0−1.642 m0
MAPbCl30.269 m0−0.816 m0MAPbBr2Cl0.223 m0−0.316 m0
MAPbI2Br0.372 m0−0.216 m0MAPbBrCl21.125 m0−1.181 m0
MAPbIBr20.688 m0−1.308 m0Path: G-F; m0 is the mass of a free electron
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Xiao, C.-L.; Liu, S.; Liu, X.-Y.; Li, Y.-N.; Zhang, P. Optoelectronic Evolution in Halogen-Doped Organic–Inorganic Halide Perovskites: A First-Principles Analysis. Molecules 2023, 28, 7341. https://doi.org/10.3390/molecules28217341

AMA Style

Xiao C-L, Liu S, Liu X-Y, Li Y-N, Zhang P. Optoelectronic Evolution in Halogen-Doped Organic–Inorganic Halide Perovskites: A First-Principles Analysis. Molecules. 2023; 28(21):7341. https://doi.org/10.3390/molecules28217341

Chicago/Turabian Style

Xiao, Cheng-Liang, Sicheng Liu, Xiao-Yan Liu, Yi-Ning Li, and Peng Zhang. 2023. "Optoelectronic Evolution in Halogen-Doped Organic–Inorganic Halide Perovskites: A First-Principles Analysis" Molecules 28, no. 21: 7341. https://doi.org/10.3390/molecules28217341

APA Style

Xiao, C. -L., Liu, S., Liu, X. -Y., Li, Y. -N., & Zhang, P. (2023). Optoelectronic Evolution in Halogen-Doped Organic–Inorganic Halide Perovskites: A First-Principles Analysis. Molecules, 28(21), 7341. https://doi.org/10.3390/molecules28217341

Article Metrics

Back to TopTop