Exploring the Impact of Intermolecular Interactions on the Glassy Phase Formation of Twist-Bend Liquid Crystal Dimers: Insights from Dielectric Studies
Abstract
:1. Introduction
2. Results
2.1. Dielectric Relaxation
2.2. Molecular Modes in the Nematic Phase
3. Discussion
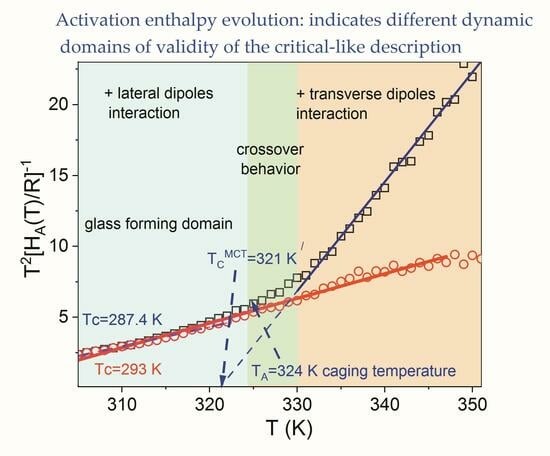
Dynamic Characterization on Glass Forming
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meyer, R.B. In Les Houches Summer School in Theoretical Physics; Balian, R.G., Weil, G., Eds.; Gordon and Breach: New York, NY, USA, 1976; pp. 273–373. [Google Scholar]
- Dozov, I. On the Spontaneous Symmetry Breaking in the Mesophases of Achiral Banana-Shaped Molecules. Europhys. Lett. 2001, 56, 247–253. [Google Scholar] [CrossRef]
- Panov, V.P.; Balachandran, R.; Nagaraj, M.; Vij, J.K.; Tamba, M.G.; Kohlmeier, A.; Mehl, G.H. Microsecond Linear Optical Response in the Unusual Nematic Phase of Achiral Bimesogens. Appl. Phys. Lett. 2011, 99, 261903-3. [Google Scholar] [CrossRef]
- Panov, V.; Balachandran, R.; Vij, J.K.; Tamba, M.G.; Kohlmeier, A.; Mehl, G.H. Field-Induced Periodic Chiral Pattern in the Nx Phase of Achiral Bimesogens. Appl. Phys. Lett. 2012, 101, 234106-4. [Google Scholar] [CrossRef]
- Cestari, M.; Diez-Berart, S.; Dunmur, D.A.; Ferrarini, A.; de la Fuente, M.R.; Jackson, D.J.B.; Lopez, D.O.; Luckhurst, G.R.; Perez-Jubindo, M.A.; Richardson, R.M.; et al. Phase Behavior and Properties of the Liquid Crystal Dimer 1″,7″-bis(4-cyanobiphenyl-4′-yl) heptane: A Twist-Bend Nematic Liquid Crystal. Phys. Rev. E 2011, 84, 031704-20. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Porada, J.H.; Hooper, J.B.; Klittnick, A.; Shen, Y.; Tuchband, M.R.; Korblova, E.; Bedrov, D.; Walba, D.M.; Glaser, M.A.; et al. Chiral Heliconical Ground State of Nanoscale Pitch in a Nematic Liquid Crystal of Achiral Molecular Dimers. Proc. Natl. Acad. Sci. USA 2013, 110, 15931–15936. [Google Scholar] [CrossRef]
- Borshch, V.; Kim, Y.K.; Xiang, J.; Gao, M.; Jákli, A.; Panov, V.P.; Vij, J.K.; Imrie, C.T.; Tamba, M.G.; Mehl, G.H.; et al. Nematic Twist-Bend Phase with Nanoscale Modulation of Molecular Orientation. Nat. Commun. 2013, 4, 2635–2638. [Google Scholar] [CrossRef]
- Meyer, C.; Luckhurst, G.; Dozov, I. Flexoelectrically Driven Electroclinic Effect in the Twist-Bend Nematic Phase of Achiral Molecules with Bent Shapes. Phys. Rev. Lett. 2013, 111, 067801-5. [Google Scholar] [CrossRef]
- Panov, V.P.; Nagaraj, M.; Vij, J.K.; Panarin, Y.P.; Kohlmeier, A.; Tamba, M.G.; Lewis, R.A.; Mehl, G.H. Spontaneous Periodic Deformations in Nonchiral Planar-Aligned Bimesogens With a Nematic-Nematic Transition and a Negative Elastic Constant. Phys. Rev. Lett. 2010, 105, 167801-4. [Google Scholar] [CrossRef]
- Henderson, P.A.; Imrie, C.T. Methylene Linked Liquid Crystal Dimers and the Twist-Bend Nematic Phase. Liq. Cryst. 2011, 38, 1407–1414. [Google Scholar] [CrossRef]
- Adlem, K.; Čopič, M.; Luckhurst, G.R.; Mertelj, A.; Parri, O.; Richardson, R.M.; Snow, B.D.; Timimi, B.A.; Tuffin, R.P.; Wilkes, D. Chemically Induced Twist-Bend Nematic Liquid Crystals, Liquid Crystal Dimers, and Negative Elastic Constants. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 88, 022503-8. [Google Scholar] [CrossRef]
- Mandle, R.J.; Davis, E.J.; Lobato, S.A.; Vol, C.-C.A.; Cowling, S.J.; Goodby, W.J. Synthesis and Characterisation of an Unsymmetrical, Ether-Linked, Fluorinated Bimesogen Exhibiting a New Polymorphism Containing the NTB or ‘twist-bend’ Phase. Phys. Chem. Chem. Phys. 2014, 16, 6907–6915. [Google Scholar] [CrossRef] [PubMed]
- Mandle, R.J.; Davis, E.J.; Archbold, C.T.; Cowling, S.J.; Goodby, W.J. Microscopy Studies of the Nematic NTB Phase of 1,11-di-(1″-cyanobiphenyl-4-yl)undecane. J. Mater. Chem. C 2014, 2, 556–566. [Google Scholar] [CrossRef]
- Mandle, R.J.; Davis, E.J.; Archbold, C.T.; Vol, C.-C.A.; Andrews, J.L.; Cowling, S.J.; Goodby, W.J. Apolar Bimesogens and the Incidence of the Twist–Bend Nematic Phase. Chem. Eur. J. 2015, 21, 8158–8167. [Google Scholar] [CrossRef] [PubMed]
- Gorecka, E.; Vaupotic, N.; Zep, A.; Pociecha, D.; Yoshioka, J.; Yamamoto, J.; Takezoe, H. A Twist-Bend Nematic (NTB) Phase of Chiral Materials. Angew. Chem. Int. Ed. 2015, 54, 10155–10159. [Google Scholar] [CrossRef] [PubMed]
- Paterson, D.A.; Gao, M.; Kim, Y.-K.; Jamali, A.; Finley, K.L.; Robles-Hernández, B.; Diez-Berart, S.; Salud, J.; de la Fuente, M.R.; Timimi, B.A.; et al. Understanding the Twist-Bend Nematic Phase: The Characterisation of 1-(4-cyanobiphenyl-4′-yloxy)-6-(4-cyanobiphenyl-4′-yl)hexane (CB6OCB) and Comparison with CB7CB. Soft Matter 2016, 12, 6827–6840. [Google Scholar] [CrossRef]
- Paterson, D.A.; Abberley, J.P.; Harrison, W.T.A.; Storey, M.D.J.; Imrie, C.T. Cyanobiphenyl-Based Liquid Crystal Dimers and the Twist-Bend Nematic Phase. Liq. Cryst. 2017, 44, 127–146. [Google Scholar] [CrossRef]
- Chen, D.; Nakata, M.; Shao, R.; Tuchband, M.R.; Shuai, M.; Baumeister, U.; Weissflog, W.; Walba, D.M.; Glaser, M.A.; Maclennan, J.E.; et al. Twist-Bend Heliconical Chiral Nematic Liquid Crystal Phase of an Achiral Rigid Bent-Core Mesogen. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 89, 022506-5. [Google Scholar] [CrossRef]
- Sreenilayam, S.P.; Panov, V.P.; Vij, J.K.; Shanker, G. The NTB Phase in an Achiral Asymmetrical Bent-Core Liquid Crystal Terminated with Symmetric Alkyl Chains. Liq. Cryst. 2017, 44, 244–253. [Google Scholar] [CrossRef]
- Merkel, K.; Kocot, A.; Vij, J.K.; Shanker, G. Distortions in Structures of the Twist Bend Nematic Phase of a Bent-Core Liquid Crystal by the Electric Field. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2018, 98, 022704-8. [Google Scholar] [CrossRef]
- Walker, R.; Pociecha, D.; Salamończyk, M.; Storey, J.M.D.; Gorecka, E.; Imrie, C.T. Supramolecular Liquid Crystals Exhibiting a Chiral Twist-Bend Nematic Phase. Mater. Adv. 2020, 1, 1622–1630. [Google Scholar] [CrossRef]
- Mandle, R.J. The Dependency of Twist-Bend Nematic Liquid Crystals on Molecular Structure: A Progression from Dimers to Trimers, Oligomers and Polymers. Soft Matter 2016, 12, 7883–7901. [Google Scholar] [CrossRef] [PubMed]
- Merkel, K.; Welch, C.; Ahmed, Z.; Piecek, W.; Mehl, G.H. Dielectric Response of Electric-Field Distortions of the Twist-Bend Nematic Phase for LC Dimers. J. Chem. Phys. 2019, 151, 114908–114920. [Google Scholar] [CrossRef] [PubMed]
- Merkel, K.; Kocot, A.; Welch, C.; Mehl, G.H. Soft Modes of the Dielectric Response in the Twist–Bend Nematic Phase and Identification of the Transition to a Nematic Splay Bend Phase in the CBC7CB Dimer. Phys. Chem. Chem. Phys. 2019, 21, 22839–22848. [Google Scholar] [CrossRef] [PubMed]
- Nordio, P.L.; Rigatti, G.; Segre, U. Dielectric Relaxation Theory in Nematic Liquids. Mol. Phys. 1973, 25, 129–136. [Google Scholar] [CrossRef]
- Coffey, W.T.; Kalmykov, Y.P. Rotational Diffusion and Dielectric Relaxation in Nematic Liquid Crystals. Adv. Chem. Phys. 2000, 113, 487–551. [Google Scholar]
- Stocchero, M.; Ferrarini, A.; Moro, G.J.; Dunmur, D.A.; Luckhurst, G.R. Molecular Theory of Dielectric Relaxation in Nematic Dimers. J. Chem. Phys. 2004, 121, 8079–8097. [Google Scholar] [CrossRef]
- Kocot, A.; Loska, B.; Arakawa, Y.; Merkel, K. Structure of the Twist-Bend Nematic Phase with Respect to the Orientational Molecular Order of the Thioether-Linked Dimers. Phys. Rev. E 2022, 105, 044701-10. [Google Scholar] [CrossRef]
- Merkel, K.; Loska, B.; Arakawa, Y.; Mehl, G.H.; Karcz, J.; Kocot, A. How Do Intermolecular Interactions Evolve at the Nematic to Twist–Bent Phase Transition? Int. J. Mol. Sci. 2022, 23, 11018. [Google Scholar] [CrossRef]
- García Colin, L.S.; del Castillo, L.F.; Goldstein, P. Theoretical Basis for the Vogel-Fulcher-Tammann Equation. Phys. Rev. B 1989, 40, 7040–7044, Erratum in Phys. Rev. B 1990, 41, 4785. [Google Scholar] [CrossRef]
- Adams, G.; Gibbs, J.H. On the Temperature Dependence of Cooperative Relaxation Properties in GlassForming Liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef]
- Cohen, M.H.; Grest, G.S. Liquid-glass transition, a free-volume approach. Phys. Rev. B 1979, 20, 1077–1098. [Google Scholar] [CrossRef]
- Bouchaud, G.P.; Biroli, G. On the Adam-Gibbs-Kirkpatrick-Thirumalai-Wolynes Scenario for the Viscosity Increase in Glasses. J. Chem. Phys. 2004, 121, 7347–7354. [Google Scholar] [CrossRef] [PubMed]
- Lubchenko, V.; Wolynes, P.G. Theory of Structural Glasses and Supercooled Liquids. Ann. Rev. Phys. Chem. 2007, 58, 235–266. [Google Scholar] [CrossRef] [PubMed]
- Colby, R.H. Dynamic Scaling Approach to Glass Formation. Phys. Rev. E 2000, 61, 1783–1792. [Google Scholar] [CrossRef] [PubMed]
- Erwin, B.M.; Colby, R.H. Temperature Dependence of Relaxation Times and the Length Scale of Cooperative Motion for Glass-Forming Liquids. J. Non-Cryst. Solids 2002, 307–310, 225–231. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Pawlus, S.; Martínez-García, J.C.; Tamarit, J.-L. Evidence for Critical-Like Behavior in Ultraslowing Glass Forming Systems. Phys. Rev. E 2010, 82, 031501-8. [Google Scholar] [CrossRef]
- Waterton, S.C. The Viscosity-Temperature Relationship and Some Inferences on the Nature of Molten and of Plastic. J. Soc. Glass. Technol. 1932, 16, 244–249. [Google Scholar]
- Mauro, J.C.; Yue, Y.; Ellison, A.J.; Gupta, P.K.; Allan, D.C. Viscosity of Glass-Forming Liquids. Proc. Natl. Acad. Sci. USA 2009, 106, 19780–19784. [Google Scholar] [CrossRef]
- Kocot, A.; Czarnecka, M.; Arakawa, Y.; Merkel, K. Dielectric Study of Liquid Crystal Dimers: Probing the Orientational Order and Molecular Interactions in Nematic and Twist-Bend Nematic Phases. Phys. Chem. B 2023, 127, 7082–7090. [Google Scholar] [CrossRef]
- López, D.O.; Sebastian, N.; de la Fuente, M.R.; Martínez-García, J.C.; Salud, J.; Pérez-Jubindo, M.A.; Diez-Berart, S.; Dunmur, D.A.; Luckhurst, G.R. Disentangling Molecular Motions Involved in the Glass Transition of a Twist-Bend Nematic Liquid Crystal Through Dielectric Studies. J. Chem. Phys. 2012, 137, 034502-10. [Google Scholar] [CrossRef]
- Pociecha, D.; Crawford, C.A.; Paterson, D.A.; Storey, J.M.D.; Imrie, C.T.; Vaupotič, N.; Gorecka, E. Critical Behavior of the Optical Birefringence at the Nematic to Twist-Bend Nematic Phase Transition. Phys. Rev. E 2018, 98, 052706-5. [Google Scholar] [CrossRef]
- Stickel, F.; Fischer, E.W.; Richert, R. Dynamics of Glass-Forming Liquids. I. Temperature-Derivative Analysis of Dielectric Relaxation Data. J. Chem. Phys. 1995, 102, 6251–6257. [Google Scholar] [CrossRef]
- Martínez-García, J.C.; Tamarit, J.L.; Rzoska, S.J. Enthalpy Space Analysis of the Evolution of the Primary Relaxation Time in Ultraslowing Systems. J. Chem. Phys. 2011, 134, 024512-7. [Google Scholar] [CrossRef]
- Arakawa, Y.; Komatsu, K.; Tsuji, H. Twist-Bend Nematic Liquid Crystals Based on Thioether Linkage. New J. Chem. 2019, 43, 6786–6793. [Google Scholar] [CrossRef]
- Arakawa, Y.; Ishida, Y.; Tsuji, H. Ether- and Thioether-Linked Naphthalene-Based Liquid-Crystal Dimers: Influence of Chalcogen Linkage and Mesogenic-Arm Symmetry on the Incidence and Stability of the Twist–Bend Nematic Phase. Chem. Eur. J. 2020, 26, 3767–3775. [Google Scholar] [CrossRef]







| Sample | Mode | log10 [τ(s)] | T0 (K) | B (K) | Tgl (K) |
|---|---|---|---|---|---|
| CBSC7SCB | m1 | −10.1 | 266.6 | 682.6 | 289.8 |
| m2 | −11.9 | 265.6 | 631.9 | 286.3 | |
| CBSC7OCB | m1 | −9.2 | 261.3 | 596.0 | 284.3 |
| m2 | −11.5 | 260.5 | 621.7 | 280.5 |
| Sample | log10 [τ(s)] | Equation (2) | Equation (9) | Range [1000/T(K−1)] |
|---|---|---|---|---|
| CBSC7SCB | −10.3 | 269 | 289 | 2.96–3.3 |
| −11.6 | 264 | 289 | 3.15–3.3 | |
| CBSC7OCB | −8.9 | 265 | 266 | 3.08–3.3 |
| −11.5 | 261 | 270 | 3.08–3.3 |
| Sample | TA | Φ (T < TA) | Tc | Φ | Range (K) | Description |
|---|---|---|---|---|---|---|
| CBSC7SCB | 324 K | 287.4 7.3 | 293 | 7.3 | 305–347 | DS |
| 321 | 1.3 | 330–351 | MCT | |||
| CBSC7OCB | 320 K | 282.5 7.0 | 287.4 | 7.0 | 295–350 | DS |
| 303.5 | 1.3 | 320–365 | MCT |
| Sample | log10 [τ(s)] | K (K) | C (K) | Tgl (K) | Range (1000/T (K−1)) |
|---|---|---|---|---|---|
| CBSC7SCB | −7.78 | 0.0789 | 3016 | 268.2 | 2.97–3.28 |
| −9.08 | 0.0082 | 3653 | 267.9 | 3.02–3.22 | |
| CBSC7OCB | −7.15 | 0.058 | 3028 | 263.9 | 3.03–3.30 |
| −9.05 | 0.031 | 3198 | 260.6 | 2.98–3.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kocot, A.; Czarnecka, M.; Arakawa, Y.; Merkel, K. Exploring the Impact of Intermolecular Interactions on the Glassy Phase Formation of Twist-Bend Liquid Crystal Dimers: Insights from Dielectric Studies. Molecules 2023, 28, 7441. https://doi.org/10.3390/molecules28217441
Kocot A, Czarnecka M, Arakawa Y, Merkel K. Exploring the Impact of Intermolecular Interactions on the Glassy Phase Formation of Twist-Bend Liquid Crystal Dimers: Insights from Dielectric Studies. Molecules. 2023; 28(21):7441. https://doi.org/10.3390/molecules28217441
Chicago/Turabian StyleKocot, Antoni, Małgorzata Czarnecka, Yuki Arakawa, and Katarzyna Merkel. 2023. "Exploring the Impact of Intermolecular Interactions on the Glassy Phase Formation of Twist-Bend Liquid Crystal Dimers: Insights from Dielectric Studies" Molecules 28, no. 21: 7441. https://doi.org/10.3390/molecules28217441
APA StyleKocot, A., Czarnecka, M., Arakawa, Y., & Merkel, K. (2023). Exploring the Impact of Intermolecular Interactions on the Glassy Phase Formation of Twist-Bend Liquid Crystal Dimers: Insights from Dielectric Studies. Molecules, 28(21), 7441. https://doi.org/10.3390/molecules28217441