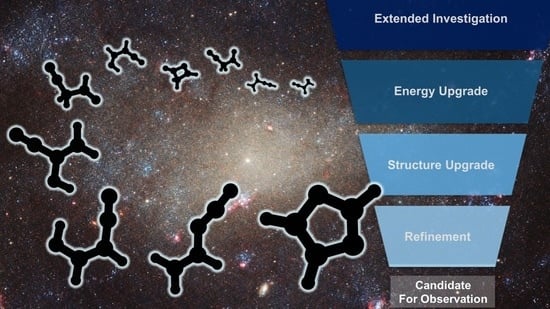
Computational Protocol for the Identification of Candidates for Radioastronomical Detection and Its Application to the C3H3NO Family of Isomers
Abstract
:1. Introduction
2. Results and Discussion
2.1. Step 1: Preliminary Investigation
2.2. Step 2: Energy Refinement
2.3. Step 3: Structure Improvement and Final Energy Refinement
2.4. Spectroscopic Characterization
3. Materials and Methods
3.1. Step 1: Preliminary Investigation
3.2. Step 2: Energy Refinement
3.3. Step 3: Structure Improvement & Final Energy Refinement
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ISM | interstellar medium |
| MEP | minimum energy principle |
| DFT | density functional theory |
| ZPE | zero-point vibrational energy |
| HF-SCF | Hartree–Fock self-consistent field |
| CC | coupled cluster |
| CCSD(T) | coupled cluster with single, double, and perturbative triple excitations |
| CBS | complete basis set |
| CV | core-valence |
| CCSDT | coupled-cluster with single, double, and triple excitations |
| CCSDT(Q) | coupled-cluster single, double, triple, and perturbative quadrupole excitations |
| DBOC | diagonal Born–Oppenheimer correction |
| MP2 | second-order Møller-Plesset perturbation theory |
| VPT2 | second-order vibrational perturbation theory (VPT2) |
| HFF | harmonic force field |
References
- McGuire, B.A. 2021 Census of Interstellar, Circumstellar, Extragalactic, Protoplanetary Disk, and Exoplanetary Molecules. Astrophys. J. Suppl. Ser. 2022, 259, 30. [Google Scholar] [CrossRef]
- CDMS, Cologne Database for Molecular Spectroscopy. Available online: cdms.astro.uni-koeln.de/classic/molecules (accessed on 1 March 2023).
- The Astrochymist: An Internet Resource for Astrochemists and Interested Bystanders. Available online: astrochymist.org (accessed on 1 March 2023).
- Garrod, R.; Belloche, A.; Müller, H.; Menten, K. Exploring molecular complexity with ALMA (EMoCA): Simulations of branched carbon-chain chemistry in Sgr B2 (N). Astron. Astrophys. 2017, 601, A48. [Google Scholar] [CrossRef] [Green Version]
- Calcutt, H.; Jørgensen, J.; Müller, H.; Kristensen, L.; Coutens, A.; Bourke, T.; Garrod, R.; Persson, M.; Van der Wiel, M.; Van Dishoeck, E.; et al. The ALMA-PILS survey: Complex nitriles towards IRAS 16293–2422. Astron. Astrophys. 2018, 616, A90. [Google Scholar] [CrossRef] [Green Version]
- Rivilla, V.M.; Jimenez-Serra, I.; Martín-Pintado, J.; Colzi, L.; Tercero, B.; De Vicente, P.; Zeng, S.; Martín, S.; García De La Concepción, J.; Bizzocchi, L.; et al. Molecular precursors of the RNA-world in space: New nitriles in the G + 0.693 − 0.027 molecular cloud. Front. Astron. Space Sci. 2022, 9, 160. [Google Scholar] [CrossRef]
- Godfrey, P.; Brown, R.; Robinson, B.; Sinclair, M. Discovery of interstellar methanimine (formaldimine). Astrophys. Lett. 1973, 13, 119. [Google Scholar]
- Zaleski, D.P.; Seifert, N.A.; Steber, A.L.; Muckle, M.T.; Loomis, R.A.; Corby, J.F.; Martinez, O.; Crabtree, K.N.; Jewell, P.R.; Hollis, J.M.; et al. Detection of E-cyanomethanimine toward Sagittarius B2 (N) in the Green Bank Telescope PRIMOS survey. Astrophys. J. Lett. 2013, 765, L10. [Google Scholar] [CrossRef]
- Loomis, R.A.; Zaleski, D.P.; Steber, A.L.; Neill, J.L.; Muckle, M.T.; Harris, B.J.; Hollis, J.M.; Jewell, P.R.; Lattanzi, V.; Lovas, F.J.; et al. The detection of interstellar ethanimine (CH3CHNH) from observations taken during the GBT PRIMOS survey. Astrophys. J. Lett. 2013, 765, L9. [Google Scholar] [CrossRef] [Green Version]
- Ligterink, N.F.W.; Calcutt, H.; Coutens, A.; Kristensen, L.; Bourke, T.; Drozdovskaya, M.N.; Müller, H.; Wampfler, S.; van Der Wiel, M.; Van Dishoeck, E.; et al. The ALMA-PILS survey: Stringent limits on small amines and nitrogen-oxides towards IRAS 16293–2422B. Astron. Astrophys. 2018, 619, A28. [Google Scholar] [CrossRef] [Green Version]
- Rivilla, V.; Martín-Pintado, J.; Jiménez-Serra, I.; Zeng, S.; Martín, S.; Armijos-Abenda no, J.; Requena-Torres, M.; Aladro, R.; Riquelme, D. Abundant Z-cyanomethanimine in the interstellar medium: Paving the way to the synthesis of adenine. Mon. Not. R. Astron. Soc. Lett. 2019, 483, L114–L119. [Google Scholar] [CrossRef] [Green Version]
- Bizzocchi, L.; Prudenzano, D.; Rivilla, V.M.; Pietropolli-Charmet, A.; Giuliano, B.M.; Caselli, P.; Martín-Pintado, J.; Jiménez-Serra, I.; Martín, S.; Requena-Torres, M.A.; et al. Propargylimine in the laboratory and in space: Millimetre-wave spectroscopy and its first detection in the ISM. Astron. Astrophys. 2020, 640, A98. [Google Scholar] [CrossRef]
- Alberton, D.; Bizzocchi, L.; Jiang, N.; Melosso, M.; Rivilla, V.; Charmet, A.P.; Giuliano, B.; Caselli, P.; Puzzarini, C.; Alessandrini, S.; et al. Laboratory spectroscopy of allylimine and tentative detection towards the G + 0.693 − 0.027 molecular cloud. Astron. Astrophys. 2023, 669, A93. [Google Scholar] [CrossRef]
- Kaifu, N.; Morimoto, M.; Nagane, K.; Akabane, K.; Iguchi, T.; Takagi, K. Detection of interstellar methylamine. Astrophys. J. 1974, 191, L135–L137. [Google Scholar] [CrossRef]
- Zeng, S.; Jiménez-Serra, I.; Rivilla, V.M.; Martín-Pintado, J.; Rodríguez-Almeida, L.F.; Tercero, B.; de Vicente, P.; Rico-Villas, F.; Colzi, L.; Martín, S.; et al. Probing the chemical complexity of amines in the ISM: Detection of vinylamine (C2H3NH2) and tentative detection of ethylamine (C2H5NH2). Astrophys. J. Lett. 2021, 920, L27. [Google Scholar] [CrossRef]
- Müller, H.S.; Belloche, A.; Xu, L.H.; Lees, R.M.; Garrod, R.T.; Walters, A.; van Wijngaarden, J.; Lewen, F.; Schlemmer, S.; Menten, K.M. Exploring molecular complexity with ALMA (EMoCA): Alkanethiols and alkanols in Sagittarius B2 (N2). Astron. Astrophys. 2016, 587, A92. [Google Scholar] [CrossRef] [Green Version]
- Rivilla, V.M.; Colzi, L.; Jiménez-Serra, I.; Martín-Pintado, J.; Megías, A.; Melosso, M.; Bizzocchi, L.; López-Gallifa, Á.; Martínez-Henares, A.; Massalkhi, S.; et al. Precursors of the RNA World in Space: Detection of (Z)-1,2-ethenediol in the Interstellar Medium, a Key Intermediate in Sugar Formation. Astrophys. J. Lett. 2022, 929, L11. [Google Scholar] [CrossRef]
- Jiménez-Serra, I.; Rodríguez-Almeida, L.F.; Martín-Pintado, J.; Rivilla, V.M.; Melosso, M.; Zeng, S.; Colzi, L.; Kawashima, Y.; Hirota, E.; Puzzarini, C.; et al. Precursors of fatty alcohols in the ISM: Discovery of n-propanol. Astron. Astrophys. 2022, 663, A181. [Google Scholar] [CrossRef]
- Colzi, L.; Rivilla, V.; Beltrán, M.; Jiménez-Serra, I.; Mininni, C.; Melosso, M.; Cesaroni, R.; Fontani, F.; Lorenzani, A.; Sánchez-Monge, A.; et al. The GUAPOS project-II. A comprehensive study of peptide-like bond molecules. Astron. Astrophys. 2021, 653, A129. [Google Scholar] [CrossRef]
- Belloche, A.; Meshcheryakov, A.; Garrod, R.; Ilyushin, V.; Alekseev, E.; Motiyenko, R.; Margulès, L.; Müller, H.; Menten, K. Rotational spectroscopy, tentative interstellar detection, and chemical modeling of N-methylformamide. Astron. Astrophys. 2017, 601, A49. [Google Scholar] [CrossRef]
- Belloche, A.; Garrod, R.; Müller, H.; Menten, K.; Medvedev, I.; Thomas, J.; Kisiel, Z. Re-exploring Molecular Complexity with ALMA (ReMoCA): Interstellar detection of urea. Astron. Astrophys. 2019, 628, A10. [Google Scholar] [CrossRef] [Green Version]
- Martín-Doménech, R.; Rivilla, V.; Jiménez-Serra, I.; Quénard, D.; Testi, L.; Martín-Pintado, J. Detection of methyl isocyanate (CH3NCO) in a solar-type protostar. Mon. Not. R. Astron. Soc. 2017, 469, 2230–2234. [Google Scholar] [CrossRef] [Green Version]
- Ligterink, N.F.; El-Abd, S.J.; Brogan, C.L.; Hunter, T.R.; Remijan, A.J.; Garrod, R.T.; McGuire, B.M. The family of amide molecules toward NGC 6334I. Astrophys. J. 2020, 901, 37. [Google Scholar] [CrossRef]
- Irvine, W.M.; Brown, R.D.; Cragg, D.M.; Friberg, P.; Godfrey, P.D.; Kaifu, N.; Matthews, H.E.; Ohishi, M.; Suzuki, H.; Takeo, H. A New Interstellar Polyatomic Molecule: Detection of Propynal in the Cold Cloud TMC-1. Astrophys. J. Lett. 1988, 335, L89. [Google Scholar] [CrossRef]
- Hollis, J.M.; Lovas, F.J.; Jewell, P.R. Interstellar Glycolaldehyde: The First Sugar. Astrophys. J. 2000, 540, L107. [Google Scholar] [CrossRef]
- Belloche, A.; Müller, H.S.P.; Menten, K.M.; Schilke, P.; Comito, C. Complex organic molecules in the interstellar medium: IRAM 30 m line survey of Sagittarius B2(N) and (M). Astron. Astrophys. 2013, 559, A47. [Google Scholar] [CrossRef] [Green Version]
- Manigand, S.; Coutens, A.; Loison, J.C.; Wakelam, V.; Calcutt, H.; Müller, H.S.P.; Jørgensen, J.K.; Taquet, V.; Wampfler, S.F.; Bourke, T.L.; et al. The ALMA-PILS survey: First detection of the unsaturated 3-carbon molecules Propenal (C2H3CHO) and Propylene (C3H6) towards IRAS 16293-2422 B. Astron. Astrophys. 2021, 645, A53. [Google Scholar] [CrossRef]
- Lattelais, M.; Pauzat, F.; Ellinger, Y.; Ceccarelli, C. Interstellar complex organic molecules and the minimum energy principle. Astrophys. J. 2009, 696, L133. [Google Scholar] [CrossRef]
- Loomis, R.A.; McGuire, B.A.; Shingledecker, C.; Johnson, C.H.; Blair, S.; Robertson, A.; Remijan, A.J. Investigating the minimum energy principle in searches for new molecular species—The case of H2C3O isomers. Astrophys. J. 2015, 799, 34. [Google Scholar] [CrossRef] [Green Version]
- Lattelais, M.; Pauzat, F.; Ellinger, Y.; Ceccarelli, C. A new weapon for the interstellar complex organic molecule hunt: The minimum energy principle. Astron. Astrophys. 2010, 519, A30. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef]
- Melli, A.; Melosso, M.; Bizzocchi, L.; Alessandrini, S.; Jiang, N.; Tonolo, F.; Boi, S.; Castellan, G.; Sapienza, C.; Guillemin, J.C.; et al. Rotational Spectra of Unsaturated Carbon Chains Produced by Pyrolysis: The Case of Propadienone, Cyanovinylacetylene, and Allenylacetylene. J. Phys. Chem. A 2022, 126, 6210–6220. [Google Scholar] [CrossRef]
- Alessandrini, S.; Melosso, M.; Jiang, N.; Bizzocchi, L.; Dore, L.; Puzzarini, C. Conformational stability of cyclopropanecarboxaldehyde is ruled by vibrational effects. Mol. Phys. 2021, 119, e1955988. [Google Scholar] [CrossRef]
- Møllendal, H.; Margulés, L.; Motiyenko, R.A.; Larsen, N.W.; Guillemin, J.C. Rotational spectrum and conformational composition of cyanoacetaldehyde, a compound of potential prebiotic and astrochemical interest. J. Phys. Chem. A 2012, 116, 4047–4056. [Google Scholar] [CrossRef]
- Behnke, M.; Medvedev, I.; Winnewisser, M.; De Lucia, F.C.; Herbst, E. The Millimeter-and Submillimeter-Wave Spectrum of Oxiranecarbonitrile. Astrophys. J. Suppl. S. 2004, 152, 97. [Google Scholar] [CrossRef] [Green Version]
- Mackrodt, W.; Wardley, A.; Curnuck, P.; Owen, N.; Sheridan, J. Microwave spectra of oxazole and isoxazole. Chem. Comm. 1966, 692–693. [Google Scholar] [CrossRef]
- Sauer, E.G.; Oja, T. Nitrogen-14 nuclear quadrupole resonance in isoxazole. J. Chem. Phys. 1973, 58, 2650–2651. [Google Scholar] [CrossRef]
- Stiefvater, O.; Nösberger, P.; Sheridan, J. Microwave spectrum and structure of isoxazole. Chem. Phys. 1975, 9, 435–444. [Google Scholar] [CrossRef]
- Kumar, A.; Sheridan, J.; Stiefvater, O.L. The microwave spectrum of oxazole I. The complete structure by DRM microwave spectroscopy. Z. Naturforsch. A 1978, 33, 145–152. [Google Scholar] [CrossRef]
- Kumar, A.; Sheridan, J.; Stiefvater, O.L. The Microwave Spectrum of Oxazole: II. Dipole Moment and Quadrupole Coupling Constants. Z. Naturforsch. A 1978, 33, 549–558. [Google Scholar] [CrossRef] [Green Version]
- Kraśnicki, A.; Pszczółkowski, L.; Kisiel, Z. Analysis of the rotational spectrum of pyruvonitrile up to 324 GHz. J. Mol. Spectrosc. 2010, 260, 57–65. [Google Scholar] [CrossRef]
- Bouchy, A.; Roussy, G. Geometrical and electronic structures of two conformers of vinyl isocyanate by microwave spectroscopy. J. Mol. Spectrosc. 1977, 68, 156–165. [Google Scholar] [CrossRef]
- Kirby, C.; Kroto, H. Microwave and photoelectron study of cis-and trans-isocyanato ethene, CH2=CHNCO (vinylisocyanate). J. Mol. Spectrosc. 1978, 70, 216–228. [Google Scholar] [CrossRef]
- Bouchy, A.; Roussy, G. The determination of the dipole moment in microwave spectroscopy: The case of cis vinyl isocyanate. J. Mol. Spectrosc. 1979, 77, 145–146. [Google Scholar] [CrossRef]
- Vávra, K.; Kolesniková, L.; Belloche, A.; Garrod, R.; Kouckỳ, J.; Uhlíková, T.; Luková, K.; Guillemin, J.C.; Kania, P.; Müller, H.; et al. Millimeter wave spectrum and search for vinyl isocyanate toward Sgr B2 (N)with ALMA. Astron. Astrophys. 2022, 666, A50. [Google Scholar] [CrossRef]
- Vijayakumar, S.; Kolandaivel, P. Isomerization of C3H3NO isomers: Ab initio study. Mol. Phys. 2006, 104, 1401–1411. [Google Scholar] [CrossRef]
- Chong, D.P.; Hu, C.H. Accurate density functional calculation of core-electron binding energies with a scaled polarized triple-zeta basis set. IV. Application to isomers of C3H6O, C3H3NO, and C6H6. J. Chem. Phys. 1998, 108, 8950–8956. [Google Scholar] [CrossRef]
- Santra, G.; Sylvetsky, N.; Martin, J.M.L. Minimally Empirical Double-Hybrid Functionals Trained against the GMTKN55 Database: RevDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A 2019, 123, 5129–5143. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Papajak, E.; Truhlar, D.G. Convergent Partially Augmented Basis Sets for Post-Hartree-Fock Calculations of Molecular Properties and Reaction Barrier Heights. J. Chem. Theory Comput. 2011, 7, 10–18. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Alessandrini, S.; Melosso, M. Fate of the Gas-Phase Reaction Between Oxirane and the CN Radical in Interstellar Conditions. Front. Astron. Space Sci. 2021, 8, 754977. [Google Scholar] [CrossRef]
- Turner, B.E.; Apponi, A.J. Microwave detection of interstellar vinyl alcohol, CH2CHOH. Astrophys. J. 2001, 561, L207. [Google Scholar] [CrossRef]
- Agúndez, M.; Marcelino, N.; Tercero, B.; Cabezas, C.; de Vicente, P.; Cernicharo, J. O-bearing complex organic molecules at the cyanopolyyne peak of TMC-1: Detection of C2H3CHO, C2H3OH, HCOOCH3, and CH3OCH3. Astron. Astrophys. 2021, 649, L4. [Google Scholar] [CrossRef] [PubMed]
- Tonolo, F.; Lupi, J.; Puzzarini, C.; Barone, V. The quest for a plausible formation route of formyl cyanide in the interstellar medium: A state-of-the-art quantum-chemical and kinetic approach. Astrophys. J. 2020, 900, 85. [Google Scholar] [CrossRef]
- Barone, V.; Biczysko, M.; Bloino, J.; Puzzarini, C. Accurate structure, thermodynamic and spectroscopic parameters from CC and CC/DFT schemes: The challenge of the conformational equilibrium in glycine. Phys. Chem. Chem. Phys. 2013, 15, 10094–10111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Puzzarini, C.; Bloino, J.; Tasinato, N.; Barone, V. Accuracy and Interpretability: The Devil and the Holy Grail. New Routes across Old Boundaries in Computational Spectroscopy. Chem. Rev. 2019, 119, 8131–8191. [Google Scholar] [CrossRef]
- Puzzarini, C.; Barone, V. The challenging playground of astrochemistry: An integrated rotational spectroscopy–quantum chemistry strategy. Phys. Chem. Chem. Phys. 2020, 22, 6507–6523. [Google Scholar] [CrossRef]
- Lupi, J.; Puzzarini, C.; Cavallotti, C.; Barone, V. State-of-the-Art Quantum Chemistry Meets Variable Reaction Coordinate Transition State Theory to Solve the Puzzling Case of the H2S + Cl System. J. Chem. Theory Comput. 2020, 16, 5090–5104. [Google Scholar] [CrossRef]
- Little, G.B.; Gerry, M. The microwave spectrum, structure, and dipole moment of propiolamide, HCCC(O)NH2. J. Mol. Spectrosc. 1978, 71, 321–342. [Google Scholar] [CrossRef]
- Hegelund, F.; Larsen, R.W.; Palmer, M. High-resolution infrared and theoretical study of gaseous oxazole in the 600–1400 cm−1 region. J. Mol. Spectr. 2007, 241, 26–44. [Google Scholar] [CrossRef]
- Puzzarini, C.; Stanton, J.F.; Gauss, J. Quantum-chemical calculation of spectroscopic parameters for rotational spectroscopy. Int. Rev. Phys. Chem. 2010, 29, 273–367. [Google Scholar] [CrossRef]
- Barone, V.; Alessandrini, S.; Biczysko, M.; Cheeseman, J.R.; Clary, D.C.; McCoy, A.B.; DiRisio, R.J.; Neese, F.; Melosso, M.; Puzzarini, C. Computational molecular spectroscopy. Nat. Rev. Methods Primers 2021, 1, 38. [Google Scholar] [CrossRef]
- Heise, H.; Scappini, F.; Dreizler, H. Acetyl Cyanide III. Vibrational Spectrum and Vibrational Analysis. Z. Naturforsch. A 1976, 31, 1408–1412. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16 Revision C.01, 2016; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Matthews, D.A.; Cheng, L.; Harding, M.E.; Lipparini, F.; Stopkowicz, S.; Jagau, T.C.; Szalay, P.G.; Gauss, J.; Stanton, J.F. Coupled-cluster techniques for computational chemistry: The CFOUR program package. J. Chem. Phys. 2020, 152, 214108. [Google Scholar] [CrossRef] [PubMed]
- Stanton, J.F.; Gauss, J.; Cheng, L.; Harding, M.E.; Matthews, D.A.; Szalay, P.G. CFOUR, Coupled-Cluster Techniques for Computational Chemistry, a Quantum-Chemical Program Package. Available online: http://www.cfour.de (accessed on 1 March 2023).
- Kállay, M.; Nagy, P.R.; Mester, D.; Rolik, Z.; Samu, G.; Csontos, J.; Csóka, J.; Szabó, P.B.; Gyevi-Nagy, L.; Hégely, B.; et al. The MRCC program system: Accurate quantum chemistry from water to proteins. J. Chem. Phys. 2020, 152, 074107. [Google Scholar] [CrossRef] [PubMed]
- Shavitt, I.; Bartlett, R.J. Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Mancini, G.; Fusè, M.; Lazzari, F.; Chandramouli, B.; Barone, V. Unsupervised search of low-lying conformers with spectroscopic accuracy: A two-step algorithm rooted into the island model evolutionary algorithm. J. Chem. Phys. 2020, 153, 124110. [Google Scholar] [CrossRef]
- León, I.; Fusè, M.; Alonso, E.R.; Mata, S.; Mancini, G.; Puzzarini, C.; Alonso, J.l.; Barone, V. Unbiased disentanglement of conformational baths with the help of microwave spectroscopy, quantum chemistry, and artificial intelligence: The puzzling case of homocysteine. J. Chem. Phys. 2022, 157, 074107. [Google Scholar] [CrossRef]
- Barone, V.; Fusè, M.; Aguado, R.; Potenti, S.; Leon, I.; Alonso, E.R.; Mata, S.; Lazzari, F.; Mancini, G.; Spada, L.; et al. Bringing Machine-Learning Enhanced Quantum Chemistry and Microwave Spectroscopy to Conformational Landscape Exploration: The Paradigmatic Case of 4-Fluoro-Threonine. Chem. Eur. J. 2023; in press. [Google Scholar] [CrossRef]
- Puzzarini, C.; Gambi, A. The energetics and structural properties of diazomethyl (HCNN) and cyanomidyl (HNCN) radicals and their related cations and anions from ab initio calculations. J. Chem. Phys. 2005, 122, 064316. [Google Scholar] [CrossRef] [PubMed]
- Feller, D.; Peterson, K.A.; Dixon, D.A. A survey of factors contributing to accurate theoretical predictions of atomization energies and molecular structures. J. Chem. Phys. 2008, 129, 204105. [Google Scholar] [CrossRef]
- Puzzarini, C. Accurate thermochemistry and spectroscopy of the oxygen-protonated sulfur dioxide isomers. Phys. Chem. Chem. Phys. 2011, 13, 21319–21327. [Google Scholar] [CrossRef]
- Alessandrini, S.; Puzzarini, C. Structural and energetic characterization of prebiotic molecules: The case study of formamide and its dimer. J. Phys. Chem. A 2016, 120, 5257–5263. [Google Scholar] [CrossRef] [PubMed]
- Feller, D. The Use of Systematic Sequences of Wave Functions for Estimating the Complete Basis Set, Full Configuration Interaction Limit in Water. J. Phys. Chem. 1993, 98, 7059–7071. [Google Scholar] [CrossRef]
- Helgaker, T.; Klopper, W.; Koch, H.; Noga, J. Basis-Set Convergence of Correlated Calculations on Water. J. Chem. Phys. 1997, 106, 9639. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. V. Core-Valence Basis Sets for Boron through Neon. J. Chem. Phys. 1995, 103, 4572. [Google Scholar] [CrossRef] [Green Version]
- Heckert, M.; Kállay, M.; Gauss, J. Molecular Equilibrium Geometries Based on Coupled-Cluster Calculations Including Quadruple Excitations. Mol. Phys. 2005, 103, 2109–2115. [Google Scholar] [CrossRef]
- Heckert, M.; Kállay, M.; Tew, D.P.; Klopper, W.; Gauss, J. Basis-Set Extrapolation Techniques for the Accurate Calculation of Molecular Equilibrium Geometries Using Coupled-Cluster Theory. J. Chem. Phys. 2006, 125, 044108. [Google Scholar] [CrossRef] [PubMed]
- Mills, I.M. Vibration–Rotation Structure in Asymmetric- and Symmetric-Top Molecules. In Molecular Spectroscopy: Modern Research; Rao, K.N., Matthews, C.W., Eds.; Academic Press: Cambridge, MA, USA, 1972; Volume 1, pp. 115–140. [Google Scholar]
- Puzzarini, C.; Stanton, J.F. Connections between the accuracy of rotational constants and equilibrium molecular structures. Phys. Chem. Chem. Phys. 2023, 25, 1421–1429. [Google Scholar] [CrossRef] [PubMed]
- Piccardo, M.; Bloino, J.; Barone, V. Generalized vibrational perturbation theory for rotovibrational energies of linear, symmetric and asymmetric tops: Theory, approximations, and automated approaches to deal with medium-to-large molecular systems. Int. J. Quantum Chem. 2015, 115, 948–982. [Google Scholar] [CrossRef] [Green Version]
- Noga, J.; Bartlett, R.J. The full CCSDT model for molecular electronic structure. J. Chem. Phys. 1987, 86, 7041–7050. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Schaefer, H.F., III. A new implementation of the full CCSDT model for molecular electronic structure. Chem. Phys. Lett. 1988, 152, 382–386. [Google Scholar] [CrossRef]
- Bomble, Y.J.; Stanton, J.F.; Kállay, M.; Gauss, J. Coupled-cluster methods including noniterative corrections for quadruple excitations. J. Chem. Phys. 2005, 123, 054101. [Google Scholar] [CrossRef]
- Kállay, M.; Gauss, J. Approximate treatment of higher excitations in coupled-cluster theory. J. Chem. Phys. 2005, 123, 214105. [Google Scholar] [CrossRef]
- Kállay, M.; Gauss, J. Approximate treatment of higher excitations in coupled-cluster theory. II. Extension to general single-determinant reference functions and improved approaches for the canonical Hartree–Fock case. J. Chem. Phys. 2008, 129, 144101. [Google Scholar] [CrossRef]
- Handy, N.C.; Yamaguchi, Y.; Schaefer, H.F., III. The diagonal correction to the Born–Oppenheimer approximation: Its effect on the singlet–triplet splitting of CH2 and other molecular effects. J. Chem. Phys. 1986, 84, 4481–4484. [Google Scholar] [CrossRef]
- Klopper, W. Simple recipe for implementing computation of first-order relativistic corrections to electron correlation energies in framework of direct perturbation theory. J. Comp. Chem. 1997, 18, 20–27. [Google Scholar] [CrossRef]
- Cowan, R.D.; Griffin, D.C. Approximate relativistic corrections to atomic radial wave functions. J. Opt. Soc. Am. 1976, 66, 1010–1014. [Google Scholar] [CrossRef]
- Rodríguez-Almeida, L.; Rivilla, V.; Jiménez-Serra, I.; Melosso, M.; Colzi, L.; Zeng, S.; Tercero, B.; de Vicente, P.; Martín, S.; Requena-Torres, M.; et al. First Detection of C2H5NCO in the ISM and Search of Other Isocyanates towards the G + 0.693-0.027 Molecular Cloud. Astron. Astrophys. 2021, 654, L1. [Google Scholar] [CrossRef]
- Cernicharo, J.; Agúndez, M.; Cabezas, C.; Marcelino, N.; Tercero, B.; Pardo, J.R.; Fuentetaja, R.; de Vicente, P. The QUIJOTE line survey of TMC-1. In Proceedings of the EPJ Web of Conferences, EDP Sciences, Sacramento, CA, USA, 24–29 July 2022; Volume 265. [Google Scholar]
- McGuire, B.A.; Burkhardt, A.M.; Loomis, R.A.; Shingledecker, C.N.; Lee, K.L.K.; Charnley, S.B.; Cordiner, M.A.; Herbst, E.; Kalenskii, S.; Momjian, E.; et al. Early science from GOTHAM: Project overview, methods, and the detection of interstellar propargyl cyanide (HCCCH2CN) in TMC-1. Astrophys. J. Lett. 2020, 900, L10. [Google Scholar] [CrossRef]





| CH2CHNCO | c-N(CH)2OCH | |||||
| trans | gauche | |||||
| Theory | Exp. | Theory | Exp. | Theory | Exp. | |
| 62,759.3 (0.28%) | 62,586.3 | 20,306.5 (0.81%) | 20,144.1 | 10,058.0 (0.07%) | 10,051.0 | |
| 2437.2 (0.02%) | 2437.8 | 3097.7 (0.31%) | 3107.5 | 9659.1 (0.14%) | 9645.8 | |
| 2346.2 (0.01%) | 2346.5 | 2684.7 (0.17%) | 2689.4 | 4924.1 (0.10%) | 4919.4 | |
| NCCH2CHO | CH3COCN | |||||
| trans | gauche | |||||
| Theory | Exp. | Theory | Exp. | Theory | Exp. | |
| 27,147.3 (1.46%) | 267,56.8 | 12,827.5 (0.12%) | 12,812.1 | 10,194.2 (0.08%) | 10,185.9 | |
| 2569.5 (0.25%) | 2576.0 | 3657.5 (0.03%) | 3658.7 | 4157.6 (0.004%) | 4157.7 | |
| 2416.9 (0.28%) | 2423.6 | 2894.5 (0.002%) | 2894.6 | 3003.5 (0.03%) | 3002.8 | |
| Parameter a | Units | (Z)-Cyanovinylalcohol | (E)-Cyanovinylalcohol | ||
|---|---|---|---|---|---|
| trans | gauche | trans | gauche | ||
| MHz | 13,893.0 | 12,869.2 | 45,505.9 | 44,451.1 | |
| MHz | 3554.5 | 3845.5 | 2387.0 | 2384.3 | |
| MHz | 2827.2 | 2956.3 | 2267.2 | 2262.0 | |
| kHz | 3.1 | 4.6 | 0.33 | 0.33 | |
| kHz | −27.3 | −32.6 | −35.7 | −32.54 | |
| kHz | 117.1 | 100.3 | 2330.0 | 1981.70 | |
| kHz | −0.95 | −1.5 | −0.041 | −0.040 | |
| Hz | −60.6 | −0.1 | −0.92 | −0.96 | |
| Hz | 0.011 | 0.025 | 0.00033 | 0.00032 | |
| Hz | −0.072 | −0.18 | −0.072 | −0.067 | |
| Hz | −0.52 | −0.28 | 2.2 | 2.2 | |
| Hz | 3.3 | 2.4 | 69.8 | 32.2 | |
| Hz | 0.0054 | 0.012 | 0.0001 | 0.0001 | |
| mHz | 0.88 | 1.8 | 0.0031 | 0.0031 | |
| mHz | 0.16 | 0.35 | 0.0013 | 0.0013 | |
| MHz | −2.1 | −1.6 | −1.3 | −3.6 | |
| − | MHz | −1.8 | −1.67 | 0.1 | 0.4 |
| MHz | 3.0 | 3.3 | 0.7 | 1.85 | |
| D | 5.45 | 2.60 | 4.78 | 4.03 | |
| D | 2.16 | 1.83 | 0.93 | 1.72 | |
| kJ mol−1 | 14.1 | 0.0 | 11.4 | 9.8 | |
| oxazole | ||||
| CC/TZ a | b | best Estimate | Exp. c | |
| 3309.09 | −126.55 | 3182.54 | ||
| 3285.40 | −126.81 | 3158.59 | ||
| 3275.62 | −125.38 | 3150.24 | ||
| 1575.76 | −35.97 | 1539.79 | ||
| 1540.35 | −43.16 | 1497.19 | ||
| 1358.40 | −32.97 | 1325.43 | 1329.75165(3) | |
| 1280.23 | −27.82 | 1252.41 | ||
| 1177.36 | −34.36 | 1143.00 | 1142.50528(3) | |
| 1112.64 | −26.01 | 1086.63 | 1091.12069(5) | |
| 1108.71 | −28.00 | 1080.70 | 1081.29060(4) | |
| 1074.50 | −23.58 | 1050.92 | 1051.75844(3) | |
| 919.16 | −13.30 | 905.86 | 909.28465(6) | |
| 908.75 | −13.73 | 895.01 | 899.33009(6) | |
| 872.69 | −18.31 | 854.38 | 859.19(1) | |
| 851.29 | −18.58 | 832.71 | 832.01870(3) | |
| 763.10 | −17.15 | 745.95 | 749.31060(3) | |
| 655.72 | −11.31 | 644.41 | 646.35537(3) | |
| 618.04 | −10.21 | 607.83 | ||
| t-vinylisocyanate | ||||
| CC/TZ a | b | best estimate | Lit. d | |
| 3270.82 | −137.94 | 3132.87 | 3149.9 | |
| 3186.24 | −132.33 | 3053.92 | 3079.0 | |
| 3168.87 | −106.84 | 3062.03 | 3051.5 | |
| 2324.44 | −60.72 | 2263.71 | 2301.7 | |
| 1689.63 | −53.05 | 1636.58 | 1635.6 | |
| 1484.92 | −28.65 | 1456.27 | 1490.3 | |
| 1405.70 | −33.45 | 1372.25 | 1408.3 | |
| 1335.24 | −26.77 | 1308.48 | 1328.3 | |
| 1115.46 | −22.70 | 1092.77 | 1109.3 | |
| 972.93 | −14.57 | 958.36 | 972.1 | |
| 899.79 | −3.96 | 895.84 | 915.6 | |
| 854.82 | 0.76 | 855.58 | 853.5 | |
| 694.68 | 1.63 | 696.31 | 698.4 | |
| 639.59 | −24.99 | 614.60 | 656.0 | |
| 573.32 | −17.43 | 555.89 | 601.1 | |
| 446.77 | −11.57 | 435.21 | 453.1 | |
| 143.04 | −2.45 | 140.58 | 136.5 | |
| 83.22 | 3.45 | 86.67 | 78.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alessandrini, S.; Melosso, M.; Rivilla, V.M.; Bizzocchi, L.; Puzzarini, C. Computational Protocol for the Identification of Candidates for Radioastronomical Detection and Its Application to the C3H3NO Family of Isomers. Molecules 2023, 28, 3226. https://doi.org/10.3390/molecules28073226
Alessandrini S, Melosso M, Rivilla VM, Bizzocchi L, Puzzarini C. Computational Protocol for the Identification of Candidates for Radioastronomical Detection and Its Application to the C3H3NO Family of Isomers. Molecules. 2023; 28(7):3226. https://doi.org/10.3390/molecules28073226
Chicago/Turabian StyleAlessandrini, Silvia, Mattia Melosso, Víctor M. Rivilla, Luca Bizzocchi, and Cristina Puzzarini. 2023. "Computational Protocol for the Identification of Candidates for Radioastronomical Detection and Its Application to the C3H3NO Family of Isomers" Molecules 28, no. 7: 3226. https://doi.org/10.3390/molecules28073226
APA StyleAlessandrini, S., Melosso, M., Rivilla, V. M., Bizzocchi, L., & Puzzarini, C. (2023). Computational Protocol for the Identification of Candidates for Radioastronomical Detection and Its Application to the C3H3NO Family of Isomers. Molecules, 28(7), 3226. https://doi.org/10.3390/molecules28073226