Temperature Dependence of the Number of Defect-Structures in Poly(vinylidene fluoride)
Abstract
:1. Introduction
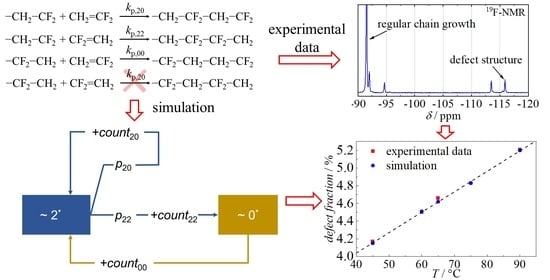
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gardiner, J. Fluoropolymers: Origin, Production, and Industrial and Commercial Applications. Aust. J. Chem. 2015, 68, 13–22. [Google Scholar] [CrossRef]
- Ameduri, B. Fluoropolymers: The right material for the right application. Chem. Eur. J. 2018, 24, 18830–18841. [Google Scholar] [CrossRef]
- Liu, F.; Hashim, N.A.; Liu, Y.; Abed, M.R.M.; Li, K. Progress in the production and modification of PVDF membranes. J. Membr. Sci. 2011, 375, 1–27. [Google Scholar] [CrossRef]
- Marcus, M.A. Ferroelectric polymers and their applications. Ferroelectrics 1982, 40, 29–41. [Google Scholar] [CrossRef]
- Martins, P.; Lopes, A.C.; Lanceros-Mendez, S. Electroactive phases of poly(vinylidene fluoride): Determination, processing and applications. Prog. Polym. Sci. 2014, 39, 683–706. [Google Scholar] [CrossRef]
- Dillon, D.R.; Tenneti, K.K.; Li, C.Y.; Ko, F.K.; Sics, I.; Hsiao, B.S. On the structure and morphology of polyvinylidene fluoride-nanoclay nanocomposites. Polymer 2006, 47, 1678–1688. [Google Scholar] [CrossRef]
- Ameduri, B. From Vinylidene Fluoride (VDF) to the Applications of VDF-Containing Polymers and Copolymers: Recent Developments and Future Trends. Chem. Rev. 2009, 109, 6632–6686. [Google Scholar] [CrossRef]
- Soulestin, T.; Ladmiral, V.; Dos Santos, F.D.; Ameduri, B. Vinylidene fluoride- and trifluoroethylene-containing fluorinated electroactive copolymers. How does chemistry impact properties? Prog. Polym. Sci. 2017, 72, 16–60. [Google Scholar] [CrossRef]
- Pladis, P.; Alexopoulos, A.H.; Kiparissides, C. Mathematical Modeling and Simulation of Vinylidene Fluoride Emulsion Polymerization. Ind. Eng. Chem. Res. 2014, 53, 7352–7364. [Google Scholar] [CrossRef]
- Brandl, F.; Beuermann, S. Semibatch Emulsion Polymerization of Vinylidene fluoride. Chem. Ing. Technol. 2018, 90, 372–379. [Google Scholar] [CrossRef]
- Boyer, C.; Valade, D.; Sauguet, L.; Ameduri, B.; Boutevin, B. Iodine Transfer Polymerization (IPT) of Vinylidene Fluoride (VDF). Influence of the Defect of VDF Chaining on the Control of ITP. Macromolecules 2005, 38, 10353–10362. [Google Scholar] [CrossRef]
- Modena, S.; Pianca, M.; Tato, M.; Moggi, G. Radical Telomerization of Vinylidene Fluoride in the Presence of 1,2-Dibromotetrafluoroethane. J. Fluor. Chem. 1989, 43, 15–25. [Google Scholar] [CrossRef]
- Maiti, P.; Nandi, A.K. Influence of Chain Structure on the Miscibility of Poly(vinylidene fluoride) with Poly(methyl acrylate). Macromolecules 1995, 28, 8511–8516. [Google Scholar] [CrossRef]
- Durand, N.; Ameduri, B.; Takashima, K.; Ishida, K.; Horie, S.; Ueda, Y. Vinylidene fluoride telomers for piezoelectric devices. Polym. J. 2011, 43, 171–179. [Google Scholar] [CrossRef]
- Lovinger, A.J.; Davis, D.D.; Cais, R.E.; Kometani, J.M. The role of molecular defects on the structure and phase transitions of poly(vinylidene fluoride). Polymer 1987, 28, 617–626. [Google Scholar] [CrossRef]
- Vohlídal, J.; Graeff, C.F.O.; Hiorns, R.C.; Jones, R.G.; Luscombe, C.; Schué, F.; Stingelin, N.; Walter, M.G. Glossary of terms relating to elevtronic, photonic and magnetic properties of polymers (IUPAC Recommendations 2021). Pure Appl. Chem. 2022, 94, 15–69. [Google Scholar] [CrossRef]
- Guerre, M.; Rahaman, S.M.W.; Ameduri, B.; Poli, R.; Ladmiral, V. Limits of Vinylidene Fluoride RAFT Polymerization. Macromolecules 2016, 49, 5386–5396. [Google Scholar] [CrossRef]
- Balague, J.; Ameduri, B.; Boutevin, B.; Caporiccio, G. Synthesis of fluorinated telomers. Part 1. Telomerization of vinylidene fluoride with perfluoroalkyl iodides. J. Fluor. Chem. 1995, 70, 215–223. [Google Scholar] [CrossRef]
- Russo, S.; Behari, K.; Chengji, S.; Pianca, M.; Barchiesi, E.; Moggi, G. Synthesis and microstructural characterization of low-molar-mass poly(vinylidene fluoride). Polymer 1993, 34, 4777–4781. [Google Scholar] [CrossRef]
- Guiot, J.; Ameduri, B.; Boutevin, B. Radical Homopolymerization of Vinylidene Fluoride Initiated by tert-Butyl Peroxypivalate. Investigation of the Microstructure by 19F and 1H NMR Spectroscopies and Mechanisms. Macromolecules 2002, 35, 8694–8707. [Google Scholar] [CrossRef]
- Ameduri, B.; Ladaviere, C.; Delolme, F.; Boutevin, B. First MALDI-TOF Mass Spectrometry of Vinylidene Fluoride Telomers Endowed with Low Defect Chaining. Macromolecules 2004, 37, 7602–7609. [Google Scholar] [CrossRef]
- Patil, Y.; Zhao, J.; Ameduri, B.; Rastogi, S. Tailoring Electroactive β- and γ-Phases via Synthesis in the Nascent Poly(vinylidene fluoride) Homopolymers. Macromolecules 2024, 57, 616–627. [Google Scholar] [CrossRef]
- Giannetti, E. Semi-crystalline fluorinated polymers. Polym. Int. 2001, 50, 10–26. [Google Scholar] [CrossRef]
- Timmerman, R. The Predominant Reaction of Some Fluorinated Polymers to Ionizing Radiation. J. Appl. Polym. Sci. 1962, 22, 456–460. [Google Scholar] [CrossRef]
- Siegmann, R.; Drache, M.; Beuermann, S. Propagation Rate Coefficients for Vinylidene Fluoride Homopolymerizations. Macromolecules 2013, 46, 9507–9514. [Google Scholar] [CrossRef]
- Schäfer, T. Kinetische Untersuchungen und PREDICI Modellierung der Pulslaserinduzierten Hochdruckpolymerisation von Vinylidenfluorid in Überkritischem Kohlendioxid. Ph.D. Thesis, TU Clausthal, Clausthal-Zellerfeld, Germany, 2017. [Google Scholar]
- Olaj, O.F.; Bitai, I.; Hinkelmann, F. The laser-flash-initiated polymerization as a tool of evaluating (individual) kinetic constants of free-radical polymerization, The direct determination of the rate constant of chain propagation. Makromol. Chem. 1987, 188, 1689–1702. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M. Rate coefficients of free-radical polymerization deduced from pulsed laser experiments. Prog. Polym. Sci. 2002, 27, 191–254. [Google Scholar] [CrossRef]
- Twum, E.B.; Li, X.; McCord, E.F.; Fox, P.A.; Lyons, D.F.; Rinaldi, P.L. 2D-NMR Studies of Polyvinylidene Fluoride. In Fluorine Containing Polymers: Advances in Fluorine-Containing Polymers; Smith, D.W., Iacono, S.T., Kettwich, S.C., Boday, D.J., Eds.; American Chemical Society: Washington, DC, USA, 2012; pp. 187–213. [Google Scholar] [CrossRef]
- Monyatsi, O.; Nikitin, A.N.; Hutchinson, R.A. Effect of Head-To-Head Addition on Vinyl Acetate Propagation Kinetics in Radical Polymerization. Macromolecules 2014, 47, 8145–8153. [Google Scholar] [CrossRef]
- Feuerpfeil, A.; Drache, M.; Jantke, L.-A.; Melchin, T.; Rodriguez-Fernandez, J.; Beuermann, S. Modeling Semi-Batch Vinyl Acetate Polymerization Processes. Ind. Eng. Chem. Res. 2021, 60, 18256–18267. [Google Scholar] [CrossRef]
- Drache, M.; Stehle, M.; Mätzig, J.; Brandl, K.; Jungbluth, M.; Namyslo, J.C.; Schmidt, A.; Beuermann, S. Identification of β scission products from free radical polymerizations of butyl acrylate at high temperature. Polym. Chem. 2019, 10, 1956. [Google Scholar] [CrossRef]
- van Herk, A.M.; Manders, L.G.; Canelas, D.A.; Quadir, M.A.; DeSimone, J.M. Propagation rate coefficients of styrene and methyl methacrylate in supercritical CO2. Macromolecules 1997, 30, 4780–4782. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M.; Isemer, C.; Lacik, I.; Wahl, A. Pressure and Temperature Dependence of the Propagation Rate Coefficient of Free-Radical Styrene Polymerization in Supercritical Carbon Dioxide. Macromolecules 2002, 35, 3866–3869. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M.; Schmaltz, C.; Kutcha, F.-D. Determination of free-radical propagation rate coefficients for methyl methacrylate and butyl acrylate homopolymerizations in fluid CO2. Macromol. Chem. Phys. 1998, 199, 1209–1216. [Google Scholar] [CrossRef]







| A20 | A22 | A00 | Ea,20 | Ea,22 | Ea,00 |
|---|---|---|---|---|---|
| L∙mol−1∙s−1 | kJ∙mol−1 | ||||
| 1.99 × 108 | 6.50 × 107 | 3.52 × 109 | 25.5 | 30.7 | 35.4 |
| T/°C | defect fractionexp/% | defect fractionsim/% | kp,app,exp /L·mol−1·s−1 | kp,app,sim /L·mol−1·s−1 |
|---|---|---|---|---|
| 45 | 4.2 | 4.2 | 11,200 | 12,700 |
| 60 | 4.5 | 4.5 | 20,000 | 19,900 |
| 65 | 4.7 | 4.6 | 23,300 | 23,000 |
| 75 | 4.8 | 4.8 | 30,900 | 30,100 |
| 90 | 5.2 | 5.2 | 46,000 | 43,800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwaderer, J.; Drache, M.; Beuermann, S. Temperature Dependence of the Number of Defect-Structures in Poly(vinylidene fluoride). Molecules 2024, 29, 1551. https://doi.org/10.3390/molecules29071551
Schwaderer J, Drache M, Beuermann S. Temperature Dependence of the Number of Defect-Structures in Poly(vinylidene fluoride). Molecules. 2024; 29(7):1551. https://doi.org/10.3390/molecules29071551
Chicago/Turabian StyleSchwaderer, Jan, Marco Drache, and Sabine Beuermann. 2024. "Temperature Dependence of the Number of Defect-Structures in Poly(vinylidene fluoride)" Molecules 29, no. 7: 1551. https://doi.org/10.3390/molecules29071551
APA StyleSchwaderer, J., Drache, M., & Beuermann, S. (2024). Temperature Dependence of the Number of Defect-Structures in Poly(vinylidene fluoride). Molecules, 29(7), 1551. https://doi.org/10.3390/molecules29071551