Temperature-Dependent Phase Behaviors in Cylinder-Forming Block Copolymers
Abstract
:1. Introduction
2. Experiments
3. Results and Discussion
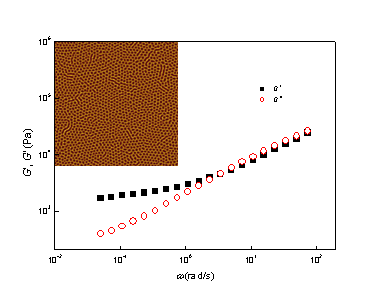
3.1. Phase Behaviors of a Highly Asymmetric Parallel Cylinder-Forming Block Copolymer
3.2. Phase Behaviors of Parallel Cylinder-Forming Block Copolymer Mixtures with a Relatively Weak Segregation Force between the Block Domains
3.3. Phase Behaviors of Perpendicular Cylinder-Forming Block Copolymer Mixture with a Strong Segregation Force between the Block Domains
3.4. Phase Behaviors of Perpendicular Cylinder-Forming Block Copolymer Mixture with an Exceptionally Strong Segregation Force between the Block Domains
4. Conclusions
References
- Bates, FS; Fredrickson, GH. Block copolymer thermodynamics: Theory and experiment. Annu. Rev. Phys. Chem 1990, 41, 525–557. [Google Scholar]
- Sakurai, S; Momii, T; Taie, K; Shibayama, M; Nomura, S; Hashimoto, T. Morphology transition from cylindrical to lamellar microdomains of block copolymers. Macromolecules 1993, 26, 485–491. [Google Scholar]
- Han, CD; Vaidya, NY; Kim, D; Shin, G; Yamaguchi, D; Hashimoto, T. Lattice disordering/ordering and demicellization/micellization transitions in highly asymmetric polystyrene-block-polyisoprene copolymers. Macromolecules 2000, 33, 3767–3780. [Google Scholar]
- Park, MJ; Char, K; Bang, J; Lodge, T. Order-disorder transition and critical micelle temperature in concentrated block copolymer solutions. Macromolecules 2005, 38, 2449–2459. [Google Scholar]
- Abuzaina, FM; Patel, AJ; Mochrie, S; Narayanan, S; Sandy, A; Garetz, BA; Balsara, NP. Structure and phase behavior of block copolymer melts near the sphere-cylinder boundary. Macromolecules 2005, 38, 7090–7097. [Google Scholar]
- Park, C; Simmons, S; Fetters, LJ; Hsiao, B; Yeh, F; Thomas, EL. Spherical to cylindrical microdomain transformation by application of a flow field. Polymer 2000, 41, 2971–2977. [Google Scholar]
- Cates, ME; Milner, ST. Role of shear in the isotropic-to-lamellar transition. Phys. Rev. Lett 1989, 62, 1856–1859. [Google Scholar]
- Balsara, NP; Hammouda, B. Shear effects on solvated block copolymer lamellae: Polystyrene-polyisoprene in dioctyl phthalate. Phys. Rev. Lett 1993, 72, 360–363. [Google Scholar]
- Ryu, CY; Lodge, TP. Thermodynamic stability and anisotropic fluctuations in the cylinder-to-sphere transition of a block copolymer. Macromolecules 1999, 32, 7190–7201. [Google Scholar]
- Ahn, DU; Sancaktar, E. Perpendicularly aligned, size- and spacing-controlled nanocylinders by molecular-weight adjustment of a homopolymer blended in an asymmetric triblock copolymer. Adv. Funct. Mat 2006, 16, 1950–1958. [Google Scholar]
- Ahn, DU; Sancaktar, E. Fabrication of well-defined block copolymer nano-cylinders by controlling the thermodynamics and kinetics involved in block copolymer self-assembly. Soft Matter 2008, 4, 1454–1466. [Google Scholar]
- Hawker, CJ; Russell, TP. Block copolymer lithography: Merging “bottom-up” with “top-down” processes. MRS Bull 2005, 30, 952–966. [Google Scholar]
- Darling, SB. Directing the self-assembly of block copolymers. Prog. Polym. Sci 2007, 32, 1152–1204. [Google Scholar]
- Lee, SH; Char, K; Kim, G. Order-disorder and order-order transitions in mixtures of highly asymmetric triblock copolymer and low molecular weight homopolymers. Macromolecules 2000, 33, 7072–7083. [Google Scholar]
- Bates, FS; Rosedale, JH; Fredrickson, GH. Fluctuation effects in a symmetric diblock copolymer near the order-disorder transition. J. Chem. Phys 1990, 92, 6255–6270. [Google Scholar]
- Sakamoto, N; Hashimoto, T; Han, CD; Kim, D; Vaidya, NY. Order-order and order-disorder transitions in a polystyrene-block-polyisoprene-block-polystyrene copolymer. Macromolecules 1997, 30, 1621–1632. [Google Scholar]
- Hamley, IW; Koppi, KA; Rosedale, JH; Bates, FS; Almdal, K; Mortensen, K. Hexagonal mesophases between lamellae and cylinders in a diblock copolymer melt. Macromolecules 1993, 26, 5959–5970. [Google Scholar]
- Khandpur, AK; Föster, S; Bates, FS; Hamley, IW; Ryan, AJ; Bras, W; Almdal, K; Mortensen, K. Polyisoprene-polystyrene diblock copolymer phase diagram near the order-disorder transition. Macromolecules 1995, 28, 8796–8806. [Google Scholar]










| Sample | Thermal History |
|---|---|
| SIS, SIS + PS2k, SIS + PS4k, SIS + PS12k, and SIS + PS15k | Annealed at 130 °C for 50 h and then rapidly quenched in liquid nitrogen (LN). |
| SIS150, SIS + PS2k150, SIS + PS12k150, and SIS + PS15k150 | First annealed at 130 °C for 47.5 h and then heated to 150 °C and held there for 2.5 h and then rapidly quenched in LN. |
| SIS170, SIS + PS4k170, SIS + PS12k170 and SIS + PS15k170 | First annealed at 130 °C for 47.5 h and then heated to 150 °C and held there for 1 h and then heated to 170 °C and held there for 1.5 h and then rapidly quenched in LN. |
| SIS + PS4k190 and SIS + PS12k190 | First annealed at 130 °C for 47.5 h and then heated to 150 °C and held there for 1 h and then heated to 170 °C and held there for 1 h and then heated to 190 °C and held there for 0.5 h and then rapidly quenched in LN. |
| SIS-210, SIS+PS4k210, SIS+PS12k210 and SIS+PS15k210 | First annealed at 130 °C for 47.5 h and then heated to 150 °C and held there for 1 h and then heated to 170 °C and held there for 0.5 h and then heated to 190 °C and held there for 0.5 h and then heated to 210 °C and held there for 0.5 h and then rapidly quenched in LN. |
| SIS + PS12k230 and SIS + PS15k230 | First annealed at 130 °C for 47.5 h and then heated to 150 °C and held there for 0.5 h and then heated to 170 °C and held there for 0.5 h and then heated to 190 °C and held there for 0.5 h and then heated to 210 °C and held there for 0.5 h and then heated to 230 °C and held there for 0.5 h and then rapidly quenched in LN. |
| SIS + PS15k250 | First annealed at 130 °C for 47.5 h and then heated to 150 °C and held there for 0.5 h and then heated to 170 °C and held there for 0.5 h and then heated to 190 °C and held there for 0.5 h and then heated to 210 °C and held there for 0.5 h and then heated to 230 °C and held there for 0.5 h and then heated to 250 °C and held there for 0.5 h rapidly quenched in LN. |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ahn, D.U.; Sancaktar, E. Temperature-Dependent Phase Behaviors in Cylinder-Forming Block Copolymers. Int. J. Mol. Sci. 2009, 10, 2169-2189. https://doi.org/10.3390/ijms10052169
Ahn DU, Sancaktar E. Temperature-Dependent Phase Behaviors in Cylinder-Forming Block Copolymers. International Journal of Molecular Sciences. 2009; 10(5):2169-2189. https://doi.org/10.3390/ijms10052169
Chicago/Turabian StyleAhn, Dae Up, and Erol Sancaktar. 2009. "Temperature-Dependent Phase Behaviors in Cylinder-Forming Block Copolymers" International Journal of Molecular Sciences 10, no. 5: 2169-2189. https://doi.org/10.3390/ijms10052169
APA StyleAhn, D. U., & Sancaktar, E. (2009). Temperature-Dependent Phase Behaviors in Cylinder-Forming Block Copolymers. International Journal of Molecular Sciences, 10(5), 2169-2189. https://doi.org/10.3390/ijms10052169