A DNA Network as an Information Processing System

Abstract

Biomolecular systems that can process information are sought for computational applications, because of their potential for parallelism and miniaturization and because their biocompatibility also makes them suitable for future biomedical applications. DNA has been used to design machines, motors, finite automata, logic gates, reaction networks and logic programs, amongst many other structures and dynamic behaviours. Here we design and program a synthetic DNA network to implement computational paradigms abstracted from cellular regulatory networks. These show information processing properties that are desirable in artificial, engineered molecular systems, including robustness of the output in relation to different sources of variation. We show the results of numerical simulations of the dynamic behaviour of the network and preliminary experimental analysis of its main components.

1. Introduction

Computing is the study of natural and artificial information processes [1]. Natural computing includes the implementation of computational paradigms abstracted from natural phenomena either on traditional electronic hardware or on alternative physical media such as in biomolecular (DNA, RNA) computing [2]. Biocompatible systems that can process information are sought for future biomedical applications. Biomolecular systems are potentially important for these and more general computational applications because of their intrinsically high information storage capabilities and parallelism.

DNA is used to build synthetic molecular machines because the simplicity of its structure and interactions allows control of its assembly through information stored in nucleotide sequences [3,4]. The Watson–Crick double helix is formed by linking together two antiparallel strands of DNA that have complementary base sequences, a process known as hybridization. Attractive interactions between complementary nucleotides contribute to the stability of the structure: adenine (A) on one strand pairs with thymine (T) on the other, while cystosine (C) pairs with guanine (G). It is the remarkable specificity of the interactions between these complementary nucleotides, together with the availability of routine commercial synthesis, that allows DNA to be used as engineering material with which to design complex systems and structures capable of self-assembly and parallel operation [3,4]. This versatile molecule has been used to design machines [5–13], finite automata [14,15], logic gates [16,17], reaction networks [18–20] and logic circuits [21,22], amongst many other structures and dynamic systems. Refer to [3,4,23] for reviews of DNA devices and machines.

Here we present preliminary work towards an autonomous, synthetic DNA network, comprised solely of DNA molecules. This DNA network implements computing paradigms abstracted from natural cellular biochemical reaction networks.

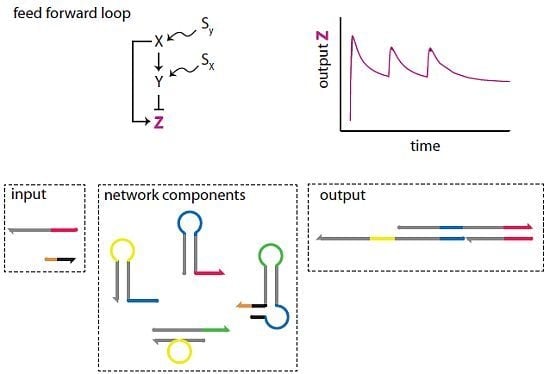
Cellular regulation is achieved through complex networks of interactions among biochemicals and cellular structures. Recurrent network motifs, classifiable in terms of function, architecture, dynamics, or biochemical process [24–26], have been identified. Alon and colleagues investigated transcription networks in the bacterium E. coli and the yeast S. cerevisiae whose information processing role is to determine the rate of production of specific proteins as a function of the environment [25,26]. In these networks, the nodes are genes and the edges represent transcriptional regulation of one gene by the protein product of another gene. Two important motifs in E. coli and S. cerevisiae transcription networks are the type-1 coherent feed-forward loop (C1-FFL) and the type-1 incoherent feed-forward loop (I1-FFL). In the C1-FFL (Figure 1a) both paths are positive: X activates both Z and an activator of Z. In the I1-FFL (Figure 1b), the direct path is positive and the indirect path is negative, i.e., X activates Z and an inhibitor of Z. Experimental and computational approaches have shown that the C1-FFL shows sign-sensitive delay that can protect against brief input fluctuations [27], whereas the I1-FFL is responsible for functions such as pulse generation [28], adaptation [29,30], fold-change detection [31] and amplitude filtering [32]. Figure 1c shows an example of pulse generation using the I1-FFL network motif.

Other networks have been investigated and display interesting information processing properties. Acar et al. [34] investigate inducibility and network-dosage invariance (i.e., invariance to the number of copies of a gene network in a cell) in the yeast galactose network. Their results revealed that, in general, the presence of two network components, one positive and one negative regulator, is the minimal requirement for network-dosage invariance.

In this work, we develop an implementation of an information processing paradigm abstracted from the yeast galactose network using DNA molecular computation. In particular, we aim to show that a DNA system can be designed and programmed to implement an information processing function that is robust to changes in network dosage and is thus capable of contributing to network behaviour that is reliable despite the stochasticity inherent in molecular systems. We choose to implement, on the DNA network, the basic information processing function of the I1-FFL: pulse generation. We note that the I1-FFL network motif [27] has two components, one positive and one negative regulator, and thus satisfies the minimal requirement for a network whose activity is robust to changes in network dosage [34].

The paper is organized as follows. Section 2 discusses the toolbox, i.e., the DNA processes and structures from which our DNA network is composed. The network itself is described in Section 3. Section 4 contains the results of numerical simulations, and conclusions are presented in Section 5.

2. The Toolbox of DNA Processes

Figure 2 illustrates an operation that is often harnessed in the design of dynamic DNA systems: toehold hybridization followed by branch migration resulting in strand displacement [35]. The system depicted in Figure 2 can be considered an information processing system that detects the presence of input S3 and releases output S1 in response. Using the same simple mechanism of toehold-mediated strand displacement, in 2006 Seelig et al. [16] showed experimental results for DNA-based digital logic circuits and in 2009, Soloveichik et al. [20] discussed reaction cascades with unimolecular and bimolecular kinetics. They illustrate their method, for example, by simulating DNA reaction modules that corresponds to the Lotka–Volterra oscillator.

Loop-containing DNA structures are interesting elements for information processing systems, as energy and information can be stored in the loop in a form that cannot readily be accessed [37,38]. The neck of the hairpin controls access to the information stored in the loop: the neck is opened using toehold-mediated strand displacement (Figure 3a). Dirks and Pierce [39] demonstrate a system of two hairpins in which the toehold required to open the neck of one is hidden in the loop of the other and vice versa. Polymerisation of the loops is triggered when one of the loops is opened by an initiator DNA.

Here, we introduce a new structure, a “gated hairpin loop” (Figure 3), that is used in our DNA network. The gated hairpin (Figure 3b) has a second level of control, i.e., a gate. A second neck controls the accessibility of the toehold used to open the loop and thus to activate the primary loop domain. Preliminary experimental results show that the loop is not opened until the gate is unlocked with the “key” K (Figure 3c). (Please refer to the Supplementary Material for methods and sequences.) The gated hairpin loop is a useful component for the implementation of the DNA network because, before unlocking the “gate”, the information held within this component is not accessible by the other network components.

3. The DNA Network Design

The DNA network is shown in Figure 4. It is abstracted from the topology and functionality of the I1-FFL network motif [27] and network-dosage invariance of the galactose signalling pathway of yeast [34]. Its abstract representation is identical to the I1-FFL shown in Figure 1b. In our DNA implementation, the nodes are complexes of DNA strands. The network has two inputs, I_x and K_y, and its activity is measured by the concentration of the output Z^*. Its design is based on the principle of toehold-mediated strand displacement (Figure 2) and the gated hairpin structure (Figure 3).

To initiate both positive and negative reaction pathways, input I_x reacts with hairpin H_x (as described in Figure 3a) forming X^* and allowing access to the toehold sequestered in the loop of H_x (blue). Following the positive reaction pathway, X^* can then react with hairpin H_z to form Z^*, in which the toehold sequestered in the loop of H_z (yellow) is activated.

Independently, and in parallel, the second input, strand K_y, activates the gated hairpin loop G_y (as described in Figure 3b), forming G_y^*. The latter reacts with X^* in the negative regulatory pathway, opening the hairpin and forming product Y^*. Y^* binds to double-stranded complex Aux in a reaction mediated by its exposed toehold (green), displacing strand Inh from Aux and forming Waste. The displaced single strand Inh hybridizes to Z^*, forming the structure InhZ in which the domain that encodes the active state of Z^* is inhibited.

The output of the network is measured by the concentration of Z^*. The toehold activated by production of Z^* (the yellow loop domain that is sequestered in hairpin H_z) is reactive and could be used to cascade downstream reactions. It could act as the input signal to another network or could be designed to regulate the production of its own initiator, input strand I_x, providing feedback to the network.

The gated hairpin loop G_y is not active unless input strand K_y is present to open its gate (Figure 3c). In the absence of input K_y, the network only has the positive reaction pathway and input I_x reacts stoichiometrically to produce output Z^*. In the presence of K_y, through production of G_y^*, a proportion of I_x is diverted to the negative reaction pathway, leading to inhibition of Z^*. The use of the gated hairpin therefore adds an independent control to the output of the network.

Because the two reaction pathways run in parallel, it is important to consider the effects of the timing of the inputs on the network behaviour. We consider two scenarios. In Scenario A, input K_y is added first, such that its reaction with G_y to form G_y^* is substantially complete before the second input I_x is added. In Scenario B, both inputs are added simultaneously. Two effects can contribute to a transient overproduction of output Z^* that is later compensated by production of Inh, resulting in a pulse of Z^*. In Scenario B, production of intermediate G_y^* does not begin until both inputs are added, so the initial reaction rate of intermediate X^* with G_y^*, corresponding to entry into the negative pathway, is zero: this guarantees a pulse of Z^*. Even in Scenario A, in which both pathways are active when I_x is added, a relative delay in the production of Inh resulting from the greater length of the negative pathway gives rise to pulse production.

This network motif is designed to operate far-from-equilibrium, as are the natural biochemical networks that inspired it. The ratios between forward and reverse reaction rates are determined by the free energy changes in each reaction and can be made large by design. Slow reverse reactions will have little effect on transient phenomena (pulse generation). However, if a sufficiently long time is allowed to elapse then reverse reactions—however slow—will ensure that the final state of the system is in thermodynamic equilibrium, independent of the details of reaction pathways. If the output of the network motif cascades forward to actuate downstream processes that are similarly far-from-equilibrium then this equilibrium state is never relevant to its operation.

3.1. Programming the DNA Network

In order to achieve a steady-state concentration of output Z^* that is invariant to network dosage, i.e., to the concentrations of network components, it is necessary to ensure that the ratio between the time-integrated quantities of input I_x (and therefore of intermediate X^*) that flow through the positive and negative reaction pathways is invariant. We assume below that the concentrations of network components H_x, H_z, G_y and Aux and of input K_y are in sufficient excess over the initial concentration of input I_x that perturbations resulting from the reactions triggered by addition of I_x are small. The rate of activation of the negative pathway depends on the concentration of intermediate G_y^* which is, in general, time-dependent and a function of the input K_y. In Scenario A, when all G_y^* is formed before I_x is added, the time-dependence of the production of K_y plays no part in the behaviour of the network. Network-dosage invariance of the steady-state output is achieved if the concentrations of H_z and the smaller of the concentrations of G_y and of K_y are scaled together ensuring a constant branching ratio between the two reaction pathways. In Scenario B, K_y and I_x are added simultaneously and the time-dependence of the production of G_y^* does affect the output of the network. In this case, network-dosage invariance is achieved if the concentrations of H_x, H_z, G_y and K_y are scaled together (see Supplementary Material). Note that the dynamic component of the network output (the pulse) is not, in general, network-dosage invariant.

The network can be configured in three ways—positive, balanced and negative—defined by its behaviour in Scenario A. The branching ratio between positive and negative pathways is determined by the concentrations of G_y^* and H_z which compete for reaction with intermediate X^*. In a balanced network, the time-integrated branching ratio is 1:1 and addition of input I_x has no effect on the steady-state concentration of output Z^*. In an unbalanced network the proportions of I_x that enter the positive and negative pathways are unequal with the result that the output concentration of Z^* is changed by addition of I_x: it can be increased or decreased (though not, of course, below zero), depending on the relative concentrations of G_y^* and H_z.

4. Simulation Results

We have investigated the behaviour of the proposed DNA network through chemical kinetics simulations. The network was modelled by the following ordinary differential equations:

$$\begin{array}{l}{H}_x+I_x\stackrel{k_1}{\to }{X}^{*}\\ X^{*}+H_z\stackrel{k_2}{\to }{Z}^{*}\\ G_y+K_y\stackrel{k_3}{\to }{G}_y^{*}\\ X^{*}+G_y^{*}\stackrel{k_4}{\to }{Y}^{*}\\ Y^{*}+Aux\stackrel{k_5}{\to }Inh+Waste\\ Z^{*}+Inh\stackrel{k_6}{\to }InhZ\end{array}$$

All reactions, with the exception of the reaction of Inh with Z^*, involve toehold-mediated strand displacement to open a secondary structure loop. Rate constants k₁ to k₆ are set at 10⁵M⁻¹s⁻¹ [35,38]. We have assumed that all reactions are irreversible (rates of reverse reactions can be six orders of magnitude slower for appropriate toehold lengths [40]). Initial concentrations of DNA molecules are specified in Supplementary Material, Table 1: concentrations of network components are of the order of 1 μM. Simulations were performed in Matlab [41] using the ODE solver ode15s.

Simulation results are shown in Figure 5. The graphs show the concentration of the network output Z^* as a function of time. Unless stated otherwise, the initial concentration of input I_x is set to 100 nM. All network components are present at t = 0 s.

Figure 5a shows simulation results for Scenario A (Section 3): input K_y is added first, at t = 0 s, and input I_x is added at t = 700 s when the reaction of K_y with G_y to produce G_y^* is substantially complete. Simulation S1 is unbalanced positively, i.e., the initial concentration of H_z is greater than that of G_y resulting in a non-zero steady-state concentration of output Z^*. In simulation 2S1, the initial concentrations of all network components are doubled: the concentration of K_y is greater than that of G_y in both cases. The two networks generate similar pulses, and the steady-state outputs of the two networks are the same, demonstrating that the steady-state output of the DNA network is robust to changes in network dosage. The same network behaviour—pulse generation and network-dosage invariant steady-state output—is displayed for balanced (S2 and 2S2) and negative (S3 and 2S3) networks.

Figure 5b shows simulation results for Scenario B: inputs I_x and K_y are delivered simultaneously at t = 0 s. S4-S6 correspond to positive, balanced and negative networks and 2S4–2S6 to the same networks in which the concentrations of network components and input K_y are doubled. Again, under these conditions the steady-state component of the output is robust to the change in network dosage. Note that, as expected, the steady-state output of the balanced network (S5) is different from the zero output of the same network in Scenario A (S2, Figure 5a): this asymmetry is a result of the initial unbalance in the network during production of G_y^*. Also shown in Figure 5b is the result of simulation S7 in which all initial concentrations are the same as in 2S5 with the exception of the concentration of K_y, which is as in S5 (half that in 2S5). The outputs of 2S5 and S7 are different, as expected, demonstrating that the concentration of input K_y must be scaled with those of network components in order to achieve network-dosage invariance.

Simulation results shown in Figure 5a,b confirm that the dynamical component of the output Z^* (the pulse) changes with network dose. (For an expanded view of the pulses in Figure 5a,b see Figure 1a,b in Supplementary Material.)

The balanced network has another robust behaviour. Once input K_y has had time to react—whether in Scenario A or Scenario B—the steady-state level of output Z^* is unchanged by subsequent addition of small quantities of input I_x. Once a steady (and balanced) concentration of G_y^* is established, these subsequent stimuli I_x cause equal activation of the positive and negative reaction pathways, resulting in a pulse of Z^* but no change in its steady-state concentration. Figure 5c shows the effects of subsequent additions of input I_x. Simulation S8 is the same as Simulation S5, except that two further quantities of I_x were added after the initial pulse of output Z^* had died away. (For a plot of the state space see Figure 2 in Supplementary Material.) The second and third additions of I_x have no effect on the steady-state output of the network, as expected. The results of Simulation S9 are also shown: S9 has the same quantity of input I_x added as in Simulation S8, except that it is all added at once at t = 0 s (initial conditions are otherwise the same as Simulations 5 and 8). The steady-state output in Simulation S9 is different from S5 and S8, demonstrating that the lack of effect of the later additions of I_x is a result of the timing of the inputs and not of saturation of the output of the network.

Figures 3–5 in Supplementary Material present additional simulation results showing robustness of output to subsequent stimuli, the limits of the desired network behaviour and results of extreme imbalance between the activation and repression pathways.

5. Conclusions

We have investigated the implementation, in a synthetic DNA reaction network, of computing paradigms abstracted from two different cellular biochemical reaction networks, the yeast galactose network [34] and the type-1 incoherent feed-forward loop network motif [27]. The results of chemical kinetics simulations show that the proposed DNA network can be programmed to implement transient pulse generation with a steady-state output that can be made robust to changes in network dosage. This network has another interesting property: it can be configured such that the steady-state output is proportional to the initial dose of one of the inputs but insensitive to subsequent additions which generate only transient output pulses.

Supplementary Material

ijms-13-05125-s001.pdf