How Common Is Disorder? Occurrence of Disordered Residues in Four Domains of Life
Abstract
:1. Introduction
2. Results and Discussion
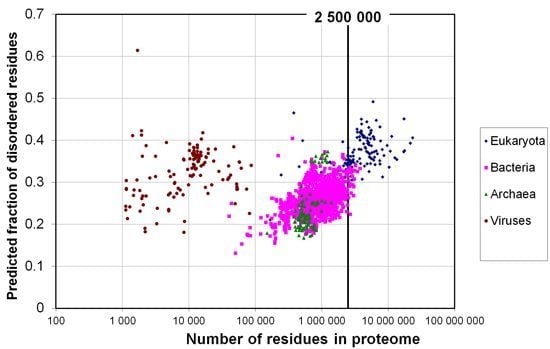
2.1. How Common Is Disorder? Prediction of Disordered Residues in 122 Proteomes







2.2. Fraction of Disordered Residues in Proteins Containing Homo-Repeats of Different Length



| B_japonicum | |||||||||||||||||
| Amino Acid | Homo-Repeat Length | ||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | >15 | |
| C | 1453 | 6768 | 364 | 11 | |||||||||||||
| M | – | 8240 | 1501 | 48 | 4 | ||||||||||||
| F | 103 | 8140 | 2477 | 119 | 6 | ||||||||||||
| I | 22 | 8229 | 3507 | 193 | 7 | ||||||||||||
| L | 5 | 8247 | 6620 | 1481 | 213 | 23 | 1 | ||||||||||
| V | 9 | 8239 | 5807 | 1010 | 103 | 2 | – | 1 | |||||||||
| W | 930 | 7312 | 496 | 18 | 1 | ||||||||||||
| Y | 386 | 7848 | 1247 | 42 | 2 | ||||||||||||
| A | – | 8253 | 7467 | 3151 | 586 | 89 | 19 | 2 | 1 | ||||||||
| G | 8 | 8242 | 5904 | 1202 | 149 | 21 | 10 | 4 | 2 | – | 1 | – | – | – | – | – | |
| T | 20 | 8229 | 4149 | 432 | 41 | 4 | 2 | ||||||||||
| S | 9 | 8241 | 4491 | 525 | 62 | 5 | 2 | 1 | 2 | – | – | 1 | |||||
| Q | 107 | 8138 | 2265 | 203 | 12 | – | – | – | – | – | – | – | 1 | ||||
| N | 195 | 8043 | 1563 | 58 | 2 | – | – | 1 | |||||||||
| E | 40 | 8206 | 3785 | 272 | 10 | 1 | 1 | ||||||||||
| D | 32 | 8214 | 4157 | 368 | 24 | 2 | 1 | 2 | |||||||||
| H | 324 | 7911 | 1215 | 87 | 9 | 2 | 1 | ||||||||||
| R | 16 | 8218 | 5771 | 968 | 102 | 17 | 3 | ||||||||||
| K | 111 | 8132 | 2401 | 157 | 10 | 3 | |||||||||||
| P | 36 | 8216 | 3810 | 473 | 76 | 19 | 8 | 5 | 1 | – | – | 1 | |||||
| B_japonicum | |||||||||||||||||
| Amino Acid | Homo-Repeat Length | ||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | >15 | |
| C | 4183 | 54,706 | 10,645 | 539 | 82 | 20 | 16 | 1 | – | – | 1 | ||||||
| M | 590 | 58,389 | 9287 | 320 | 17 | – | 1 | 2 | |||||||||
| F | 2011 | 56,921 | 20,466 | 1535 | 146 | 30 | 12 | 10 | 2 | 1 | 1 | ||||||
| I | 1886 | 57,053 | 24,782 | 2218 | 118 | 21 | 2 | 1 | – | 1 | |||||||
| L | 296 | 58,704 | 47,078 | 15,204 | 2697 | 918 | 185 | 131 | 57 | 39 | 17 | 13 | – | 1 | – | 1 | |
| V | 681 | 58,306 | 17,587 | 4911 | 458 | 40 | 9 | ||||||||||
| W | 7492 | 51,379 | 4293 | 108 | 3 | 1 | |||||||||||
| Y | 3959 | 54,975 | 14,416 | 854 | 53 | 5 | 2 | ||||||||||
| A | 590 | 58,370 | 39,712 | 10,362 | 2011 | 671 | 311 | 180 | 82 | 81 | 43 | 28 | 18 | 21 | 17 | 9 | |
| G | 603 | 58,383 | 35,065 | 7075 | 1460 | 461 | 209 | 138 | 66 | 27 | 30 | 23 | 12 | 7 | 6 | 7 | |
| T | 718 | 58,220 | 28,359 | 3512 | 416 | 130 | 43 | 14 | 5 | 3 | – | 2 | 1 | 1 | |||
| S | 303 | 58,692 | 42,712 | 13,046 | 2925 | 699 | 259 | 122 | 69 | 52 | 25 | 24 | 16 | 5 | 10 | – | |
| Q | 1197 | 57,773 | 25,784 | 3675 | 567 | 216 | 131 | 63 | 53 | 19 | 46 | 15 | 11 | 4 | 13 | 17 | |
| N | 2414 | 56,528 | 18,282 | 1446 | 92 | 21 | – | 2 | – | – | 1 | ||||||
| E | 898 | 58,037 | 38,361 | 10,830 | 2461 | 852 | 381 | 261 | 144 | 86 | 42 | 18 | 17 | 30 | 10 | 14 | |
| D | 1511 | 57,465 | 24,695 | 1769 | 405 | 144 | 47 | 17 | 29 | 2 | – | 1 | 1 | 2 | 5 | 1 | |
| H | 3230 | 55,669 | 13,649 | 842 | 116 | 41 | 26 | 26 | 14 | 29 | 9 | 8 | 5 | 2 | 1 | 2 | |
| R | 785 | 58,172 | 18,597 | 6686 | 1080 | 212 | 48 | 6 | 3 | 3 | 1 | 1 | – | – | – | – | |
| K | 1423 | 57,514 | 32,501 | 6424 | 1083 | 263 | 102 | 47 | 64 | 66 | 18 | – | 2 | 3 | 1 | 1 | |
| P | 891 | 58,076 | 17,653 | 8799 | 2173 | 774 | 357 | 219 | 114 | 69 | 55 | 26 | 16 | 18 | 2 | 6 | |
3. Experimental Section
3.1. Proteomes
| Eukaryota | Eukaryota (Fungi) | Bacteria *** | ||
|---|---|---|---|---|
| Metazoa | 25.H_sapiens; 22974.B_taurus; 59.M_musculus; 122.R_norvegicus; 21457.G_gallus; 20721.D_rerio; 22388.T_nigroviridis; 17.D_melanogaster; 25396.D_pseudoobscura; 31436.A_aegypti; 78607.A_darlingi; 22426.A_gambiae; 21633.C_briggsae; 9.C_elegans; 64800.L_loa; 79720.T_spiralis; 30565.N_vectensis | 34310.A_capsulata_ATCC_26029; 34967.A_capsulata_H143; 34495.A_dermatitidis_SLH14081; 34498.A_dermatitidis_ER-3; 35919.A_benhamiae; 29154.A_clavatus; 33020.A_flavus; 22118.A_fumigatus_FGSC_A1100; 31018.A_fumigatus_CEA10; 29130.A_niger; 23077.A_oryzae; 28239.A_terreus; 30100.B_fuckeliana; 22024.C_albicans_SC5314; 32738.C_dubliniensis; 19665.C_glabrata; 34491.C_tropicalis; 25585.C_globosum_IFO_6347; 34493.C_lusitaniae; 34218.C_posadasii; 79902.C_graminicola; 20018.D_hansenii; 34482.L_thermotolerans; 29447.L_elongisporus; 22028.M_oryzae; | Acidobacteria | 25797.S_usitatus 37022.A_mediterranei; 33926.C_acidiphila; 35278.Frankia_sp_EuI1c; 35534.F_sp; 74443.K_setae; 33113.R_opacus; 25456.Rhodococcus_sp; 131.S_avermitilis; 36666.S_bingchenggensis; 84.S_coelicolor; 34910.S_scabies; 58962.S_violaceusniger; 34011.S_roseum |
| Viridiplantae | 23214.O_sativa; 3.A_thaliana; 33157.Micromonas_sp; 29351.O_lucimarinus; 25972.O_tauri | 34471.N_otae; 34970.N_haematococca; 29157.N_fischeri; 22025.N_crassa; 34307.P_brasiliensis_Pb03; 34389.P_brasiliensis_Pb18; 34392.P_brasiliensis_ATCC_MYA‑826; 31898.P_chrysogenum; | Proteobacteria | 112.B_japonicum; 22343.Burkholderia_sp_ATCC_17760; 25388.B_xenovorans; 33223.H_ochraceum; 23351.M_xanthus; 32044.P_pacifica; 30295.S_cellulosum; 33616.S_aurantiaca |
| Stramenopiles * | 35109.E_siliculosus | 32999.P_marneffei 25591.P_nodorum; 29448.P_guilliermondii; | Bacteroidetes | 33930.C_pinensis; 32144.M_marina |
| Choanoflagellida ** | 30562.M_brevicollis | 28727.P_stipitis; 79908.P_graminis; | Chloroflexi | 36622.K_racemifer |
| Amoebozoa * | 21395.D_discoideum; 35301.P_pallidum | 30091.S_cerevisiae_YJM789; 31651.S_cerevisiae_RM11-1a; 34506.S_cerevisiae_JAY291; 35062.S_cerevisiae_Lalvin_EC1118; 71242.S_cerevisiae; 30103.S_sclerotiorum; 35280.S_macrospora; 33056.T_stipitatus; 35921.T_verrucosum; 34386.U_reesii; 30097.V_polyspora; 35359.V_albo-atrum; 20011.Y_lipolytica; 31020.C_cinerea; 20846.C_neoformans_JEC21; 21380.C_neoformans_B-3501A; 31023.L_bicolor; 33031.P_placenta; 22029.U_maydis | ||
3.2. Prediction of Disordered Residues
| Method | Sw | AUC |
|---|---|---|
| CSpritz [25] (Walsh et al., 2011) | 0.571 | 0.877 |
| IsUnstruct [18] version 2.02 (Lobanov et al., 2013) | 0.567 | 0.856 |
| IUPred (long) [26] (Dosztanyi et al., 2005) | 0.426 | 0.818 |
| PONDR-FIT [24] (Xue et al., 2010) | 0.515 | 0.817 |
| FoldUnfold [20] (Galzitskaya et al., 2006) | 0.446 | 0.813 |
| DISOPRED [27] (Ward et al., 2004) | 0.462 | 0.806 |



| Domain | Number | Our Definition | Rough Definition | Difference |
|---|---|---|---|---|
| Eukaryota | 137 | 0.366 | 0.319 | 0.047 |
| Bacteria | 1540 | 0.260 | 0.151 | 0.109 |
| Archaea | 105 | 0.236 | 0.128 | 0.108 |
| Viruses | 120 | 0.282 | 0.176 | 0.106 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sigrist, C.J.A.; Cerutti, L.; de Castro, E.; Langendijk-Genevaux, P.S.; Bulliard, V.; Bairoch, A.; Hulo, N. PROSITE, a protein domain database for functional characterization and annotation. Nucleic Acids Res. 2010, 38, D161–D166. [Google Scholar] [CrossRef] [PubMed]
- Hunter, S.; Apweiler, R.; Attwood, T.K.; Bairoch, A.; Bateman, A.; Binns, D.; Bork, P.; Das, U.; Daugherty, L.; Duquenne, L.; et al. InterPro: The integrative protein signature database. Nucleic Acids Res. 2009, 37, D211–D215. [Google Scholar] [CrossRef] [PubMed]
- Finn, R.D.; Mistry, J.; Tate, J.; Coggill, P.; Heger, A.; Pollington, J.E.; Gavin, O.L.; Gunasekaran, P.; Ceric, G.; Forslund, K.; et al. The Pfam protein families database. Nucleic Acids Res. 2010, 38, D211–D222. [Google Scholar] [CrossRef] [PubMed]
- Potenza, E.; di Domenico, T.; Walsh, I.; Tosatto, S.C.E. MobiDB 2.0: An improved database of intrinsically disordered and mobile proteins. Nucleic Acids Res. 2015, 43, D315–D320. [Google Scholar] [CrossRef] [PubMed]
- Pietrosemoli, N.; García-Martín, J.A.; Solano, R.; Pazos, F. Genome-wide analysis of protein disorder in Arabidopsis thaliana: Implications for plant environmental adaptation. PLoS ONE 2013, 8, e55524. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, J.; Grahn, M.; Wright, A.P.H. Proteome-wide evidence for enhanced positive Darwinian selection within intrinsically disordered regions in proteins. Genome Biol. 2011, 12, R65. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, M.Y.; Furletova, E.I.; Bogatyreva, N.S.; Roytberg, M.A.; Galzitskaya, O.V. Library of disordered patterns in 3D protein structures. PLoS Comput. Biol. 2010, 6, e1000958. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, M.Y.; Galzitskaya, O.V. Disordered patterns in clustered Protein Data Bank and in eukaryotic and bacterial proteomes. PLoS ONE 2011, 6, e27142. [Google Scholar] [CrossRef] [PubMed]
- Jorda, J.; Xue, B.; Uversky, V.N.; Kajava, A.V. Protein tandem repeats—The more perfect, the less structured. FEBS J. 2010, 277, 2673–2682. [Google Scholar] [CrossRef] [PubMed]
- Hengen, P. Purification of His-Tag fusion proteins from Escherichia coli. Trends Biochem. Sci. 1995, 20, 285–286. [Google Scholar] [CrossRef]
- Serdiuk, I.N.; Galzitskaia, O.V. Unstructured regions in elongation factors EF1A from three overkingdom of the living world. Mol. Biol. 2007, 41, 1042–1055. [Google Scholar]
- Karlin, S. Statistical significance of sequence patterns in proteins. Curr. Opin. Struct. Biol. 1995, 5, 360–371. [Google Scholar] [CrossRef]
- Lagier-Tourenne, C.; Cleveland, D.W. Neurodegeneration: An expansion in ALS genetics. Nature 2010, 466, 1052–1053. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Dion, P.; Laganiere, J.; Brais, B.; Rouleau, G.A. Oligomerization of polyalanine expanded PABPN1 facilitates nuclear protein aggregation that is associated with cell death. Hum. Mol. Genet. 2001, 10, 2341–2351. [Google Scholar] [CrossRef] [PubMed]
- Sackewitz, M.; Scheidt, H.A.; Lodderstedt, G.; Schierhorn, A.; Schwarz, E.; Huster, D. Structural and dynamical characterization of fibrils from a disease-associated alanine expansion domain using proteolysis and solid-state NMR spectroscopy. J. Am. Chem. Soc. 2008, 130, 7172–7173. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, M.Y.; Sokolovskiy, I.V.; Galzitskaya, O.V. HRaP: Database of occurrence of HomoRepeats and patterns in proteomes. Nucleic Acids Res. 2014, 42, D273–D278. [Google Scholar] [CrossRef] [PubMed]
- Galzitskaya, O.V.; Lobanov, M.Y. Phyloproteomic analysis of 11,780 six-residue-long motifs occurrences. Biomed. Res. Int. 2015, 2015, 208346. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, M.Y.; Sokolovskiy, I.V.; Galzitskaya, O.V. IsUnstruct: Prediction of the residue status to be ordered or disordered in the protein chain by a method based on the Ising model. J. Biomol. Struct. Dyn. 2013, 31, 1034–1043. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, M.Y.; Galzitskaya, O.V. The Ising model for prediction of disordered residues from protein sequence alone. Phys. Biol. 2011, 8, 035004. [Google Scholar] [CrossRef] [PubMed]
- Galzitskaya, O.V.; Garbuzynskiy, S.O.; Lobanov, M.Y. FoldUnfold: Web server for the prediction of disordered regions in protein chain. Bioinform. Oxf. Engl. 2006, 22, 2948–2949. [Google Scholar] [CrossRef] [PubMed]
- Bogatyreva, N.S.; Finkelstein, A.V.; Galzitskaya, O.V. Trend of amino acid composition of proteins of different taxa. J. Bioinform. Comput. Biol. 2006, 4, 597–608. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Dunker, A.K.; Uversky, V.N. Orderly order in protein intrinsic disorder distribution: Disorder in 3500 proteomes from viruses and the three domains of life. J. Biomol. Struct. Dyn. 2012, 30, 137–149. [Google Scholar] [CrossRef] [PubMed]
- Syutkin, A.S.; Pyatibratov, M.G.; Galzitskaya, O.V.; Rodríguez-Valera, F.; Fedorov, O.V. Haloarcula marismortui archaellin genes as ecoparalogs. Extrem Life Extreme Cond. 2014, 18, 341–349. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Dunbrack, R.L.; Williams, R.W.; Dunker, A.K.; Uversky, V.N. PONDR-FIT: A meta-predictor of intrinsically disordered amino acids. Biochim. Biophys. Acta 2010, 1804, 996–1010. [Google Scholar] [CrossRef] [PubMed]
- Walsh, I.; Martin, A.J.M.; di Domenico, T.; Vullo, A.; Pollastri, G.; Tosatto, S.C.E. CSpritz: Accurate prediction of protein disorder segments with annotation for homology, secondary structure and linear motifs. Nucleic Acids Res. 2011, 39, W190–W196. [Google Scholar] [CrossRef] [PubMed]
- Dosztányi, Z.; Csizmok, V.; Tompa, P.; Simon, I. IUPred: Web server for the prediction of intrinsically unstructured regions of proteins based on estimated energy content. Bioinformatics 2005, 21, 3433–3434. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.J.; McGuffin, L.J.; Bryson, K.; Buxton, B.F.; Jones, D.T. The DISOPRED server for the prediction of protein disorder. Bioinformatics 2004, 20, 2138–2139. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Yan, J.; Fan, X.; Mizianty, M.J.; Xue, B.; Wang, K.; Hu, G.; Uversky, V.N.; Kurgan, L. Exceptionally abundant exceptions: Comprehensive characterization of intrinsic disorder in all domains of life. Cell. Mol. Life Sci. 2015, 72, 137–151. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobanov, M.Y.; Galzitskaya, O.V. How Common Is Disorder? Occurrence of Disordered Residues in Four Domains of Life. Int. J. Mol. Sci. 2015, 16, 19490-19507. https://doi.org/10.3390/ijms160819490
Lobanov MY, Galzitskaya OV. How Common Is Disorder? Occurrence of Disordered Residues in Four Domains of Life. International Journal of Molecular Sciences. 2015; 16(8):19490-19507. https://doi.org/10.3390/ijms160819490
Chicago/Turabian StyleLobanov, Mikhail Yu., and Oxana V. Galzitskaya. 2015. "How Common Is Disorder? Occurrence of Disordered Residues in Four Domains of Life" International Journal of Molecular Sciences 16, no. 8: 19490-19507. https://doi.org/10.3390/ijms160819490
APA StyleLobanov, M. Y., & Galzitskaya, O. V. (2015). How Common Is Disorder? Occurrence of Disordered Residues in Four Domains of Life. International Journal of Molecular Sciences, 16(8), 19490-19507. https://doi.org/10.3390/ijms160819490