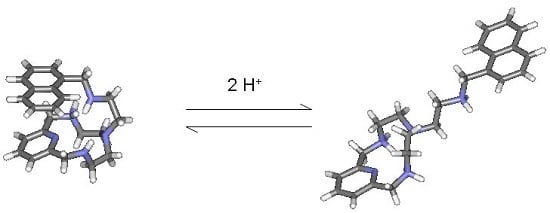
Molecular Rearrangement of an Aza-Scorpiand Macrocycle Induced by pH: A Computational Study †
Abstract
:1. Introduction
2. Results and Discussion
2.1. Conformational Search
2.2. Comparison of Total Energies
3. Methods
3.1. Monte Carlo Multiple Minimum
3.2. Calculation of Energies
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kinbara, K.; Aida, T. Toward intelligent molecular machines: Directed motions of biological and artificial molecules and assemblies. Chem. Rev. 2005, 105, 1377–1400. [Google Scholar] [CrossRef] [PubMed]
- Pallavicini, P.S.; Perotti, A.; Poggi, A.; Seghi, B.; Fabbrizzi, L. N-(aminoethyl) cyclam: A tetraaza macrocycle with a coordinating tail (scorpiand). Acidity controlled coordination of the side chain to nickel(II) and nickel(III) cations. J. Am. Chem. Soc. 1987, 109, 5139–5144. [Google Scholar] [CrossRef]
- Bencini, A.; Berni, E.; Bianchi, A.; Fornasari, P.; Giorgi, C.; Lima, J.C.; Pina, F. A fluorescent chemosensor for Zn(II). Exciplex formation in solution and the solid state. Dalton Trans. 2004, 14, 2180–2187. [Google Scholar] [CrossRef] [PubMed]
- Blasco, S.; Verdejo, B.; Bazzicalupi, C.; Bianchi, A.; Giorgi, C.; Soriano, C.; García-España, E. A thermodynamic insight into the recognition of hydrophilic and hydrophobic amino acids in pure water by aza-scorpiand type receptors. Org. Biomol. Chem. 2015, 13, 843–850. [Google Scholar] [CrossRef] [PubMed]
- Bernier, N.; Esteves, C.V.; Delgado, R. Heteroditopic receptor based on crown ether and cyclen units for the recognition of zwitterionic amino acids. Tetrahedron 2012, 68, 4860–4868. [Google Scholar] [CrossRef]
- Aydın, I.; Aral, T.; Karakaplan, M.; Hoşgören, H. Chiral lariat ethers as membrane carriers for chiral amino acids and their sodium and potassium salts. Tetrahedron Asymmetry 2009, 20, 179–183. [Google Scholar] [CrossRef]
- Verdejo, B.; Acosta-Rueda, L.; Clares, M.P.; Aguinaco, A.; Basallote, M.G.; Soriano, C.; García-España, E. Equilibrium, kinetic, and computational studies on the formation of Cu2+ and Zn2+ complexes with an indazole-containing azamacrocyclic scorpiand: Evidence for metal-induced tautomerism. Inorg. Chem. 2015, 54, 1983–1991. [Google Scholar] [CrossRef] [PubMed]
- Verdejo, B.; Ferrer, A.; Blasco, S.; Castillo, C.E.; González, J.; Latorre, J.; García-España, E. Hydrogen and copper ion-induced molecular reorganizations in scorpionand-like ligands. A potentiometric, mechanistic, and solid-state study. Inorg. Chem. 2007, 46, 5707–5719. [Google Scholar] [CrossRef] [PubMed]
- de Julián-Ortiz, J.; Verdejo, B.; Polo, V.; Besalú, E.; García-España, E. Molecular Rearrangement of an Aza-Scorpiand Macrocycle Induced by pH. A Computational Study. In Sciforum Electronic Conference Series, Proceedings of the MOL2NET, Bizkaia, Spain, 5–15 December 2015.
- Valencia, L.; Bastida, R.; García-España, E.; de Julián-Ortiz, J.V.; Llinares, J.M.; Macías, A.; Pérez Lourido, P. Nitrate encapsulation within the cavity of polyazapyridinophane. Considerations on nitrate-pyridine interactions. Cryst. Growth Des. 2010, 10, 3418–3423. [Google Scholar] [CrossRef]
- Chang, G.; Guida, W.C.; Still, W.C. An internal-coordinate Monte Carlo method for searching conformational space. J. Am. Chem. Soc. 1989, 111, 4379–4386. [Google Scholar] [CrossRef]
- Saunders, M.; Houk, K.N.; Wu, Y.D.; Still, W.C.; Lipton, M.; Chang, G.; Guida, W.C. Conformations of cycloheptadecane. A comparison of methods for conformational searching. J. Am. Chem. Soc. 1990, 112, 1419–1427. [Google Scholar] [CrossRef]
- Kolossváry, I.; Guida, W.C. Torsional flexing: Conformational searching of cyclic molecules in biased internal coordinate space. J. Comput. Chem. 1993, 14, 691–698. [Google Scholar] [CrossRef]
- Allinger, N.L. Conformational analysis. 130. MM2. A hydrocarbon force field utilizing V1 and V2. J. Am. Chem. Soc. 1977, 99, 8127–8134. [Google Scholar] [CrossRef]
- Bushuev, Y.G.; Sastre, G.; de Julian-Ortiz, J.V. The structural directing role of water and hydroxyl groups in the synthesis of beta zeolite polymorphs. J. Phys. Chem. C 2009, 114, 345–356. [Google Scholar] [CrossRef]
- Bushuev, Y.G.; Sastre, G.; de Julian-Ortiz, J.V.; Gálvez, J. Water–hydrophobic zeolite systems. J. Phys. Chem. C 2012, 116, 24916–24929. [Google Scholar] [CrossRef]
- Bultinck, P.; Gironés, X.; Carbo-Dorca, R. Molecular quantum similarity: Theory and applications. Rev. Comput. Chem. 2005, 21, 127. [Google Scholar]
- Hypercube Inc. HYPERCHEM. Version 7.5; Gainsville, FL, USA, 2002. [Google Scholar]
- MOPAC2016, Version: 16.060W, James J.P. Stewart, Stewart Computational Chemistry. Available online: http://OpenMOPAC.net (accessed on 13 July 2016).
- Versluis, L.; Ziegler, T. The determination of molecular structures by density functional theory. The evaluation of analytical energy gradients by numerical integration. J. Chem. Phys. 1988, 88, 322–328. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993, 2, 799–805. [Google Scholar] [CrossRef]
- Pye, C.C.; Ziegler, T. An implementation of the conductor-like screening model of solvation within the Amsterdam density functional package. Theor. Chem. Acc. 1999, 101, 396–408. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K. Comparison shopping for a gradient-corrected density functional. Int. J. Quantum Chem. 1996, 57, 309–319. [Google Scholar] [CrossRef]
- ADF2006.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available online: http://www.scm.com (accessed on 13 July 2016).




| Conformation | Torsions Allowed | a | b | c | d | e |
|---|---|---|---|---|---|---|
| A | - | −146.8 | 74.4 | −170.9 | 80.7 | 77.0 |
| 1 | 12-ring, d | −148.4 | 59.1 | 176.8 | 144.9 | 66.3 |
| 2 | 12-ring, b, d | 68.2 | 179.2 | −91.2 | 71.3 | 74.7 |
| 3 | a, b | −67.9 | −175.5 | 94.2 | −67.3 | 105.3 |
| 4 | d | −62.6 | −167.8 | −177.3 | −176.9 | −814 |
| 5 | 12-ring, a | −154.9 | 170.8 | 177.6 | 172.9 | −87.1 |
| B | - | 69.4 | −176.5 | −177.2 | −179.2 | 84.6 |
| Conformation | Smallest Box Enclosing Solute/Å | Cubic Periodic Box Edge/Å | Maximum Number of Water Molecules | ||
|---|---|---|---|---|---|
| X | Y | Z | |||
| A | 6.90 | 6.19 | 7.73 | 18.10 | 216 |
| 1 | 7.65 | 5.87 | 7.80 | 18.10 | 216 |
| 2 | 8.08 | 6.91 | 9.07 | 18.10 | 216 |
| 3 | 7.76 | 5.71 | 10.75 | 21.51 | 329 |
| 4 | 7.49 | 5.42 | 15.48 | 30.96 | 980 |
| 5 | 7.30 | 5.17 | 19.91 | 31.81 | 1064 |
| B | 6.90 | 3.29 | 17.62 | 35.25 | 1447 |
| Starting Conformation | Number of H+ | Method | Environment Simulation Method | Total Energy/kcal/mol 2 | Difference A–B/kcal/mol |
|---|---|---|---|---|---|
| A | 1 | PM3 | vacuum | −6124.84 | −9.14 |
| B | 1 | PM3 | vacuum | −6115.70 | |
| A | 3 | PM3 | vacuum | −5752.39 | −14.13 |
| B | 3 | PM3 | vacuum | −5757.88 | |
| A | 1 | PM7 | vacuum | −99257.16 | 5.49 |
| B | 1 | PM7 | vacuum | −99257.00 | |
| A | 3 | PM7 | vacuum | −99411.69 | −0.16 |
| B | 3 | PM7 | vacuum | −99424.32 | |
| A | 1 | LDA/QZ4P | COSMO | −9171.05 | −6.42 |
| B | 1 | LDA/QZ4P | COSMO | −9162.84 | |
| A | 3 | LDA/QZ4P | COSMO | −9133.36 | 12.63 |
| B | 3 | LDA/QZ4P | COSMO | −9134.40 | |
| A | 3 | GGA-BP/TZ2P | vacuum | −8396.54 | −8.21 |
| B | 3 | GGA-BP/TZ2P | vacuum | −8408.01 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Julián-Ortiz, J.V.; Verdejo, B.; Polo, V.; Besalú, E.; García-España, E. Molecular Rearrangement of an Aza-Scorpiand Macrocycle Induced by pH: A Computational Study. Int. J. Mol. Sci. 2016, 17, 1131. https://doi.org/10.3390/ijms17071131
De Julián-Ortiz JV, Verdejo B, Polo V, Besalú E, García-España E. Molecular Rearrangement of an Aza-Scorpiand Macrocycle Induced by pH: A Computational Study. International Journal of Molecular Sciences. 2016; 17(7):1131. https://doi.org/10.3390/ijms17071131
Chicago/Turabian StyleDe Julián-Ortiz, Jesus Vicente, Begoña Verdejo, Víctor Polo, Emili Besalú, and Enrique García-España. 2016. "Molecular Rearrangement of an Aza-Scorpiand Macrocycle Induced by pH: A Computational Study" International Journal of Molecular Sciences 17, no. 7: 1131. https://doi.org/10.3390/ijms17071131
APA StyleDe Julián-Ortiz, J. V., Verdejo, B., Polo, V., Besalú, E., & García-España, E. (2016). Molecular Rearrangement of an Aza-Scorpiand Macrocycle Induced by pH: A Computational Study. International Journal of Molecular Sciences, 17(7), 1131. https://doi.org/10.3390/ijms17071131