Conformation-Independent QSPR Approach for the Soil Sorption Coefficient of Heterogeneous Compounds
Abstract
:1. Introduction
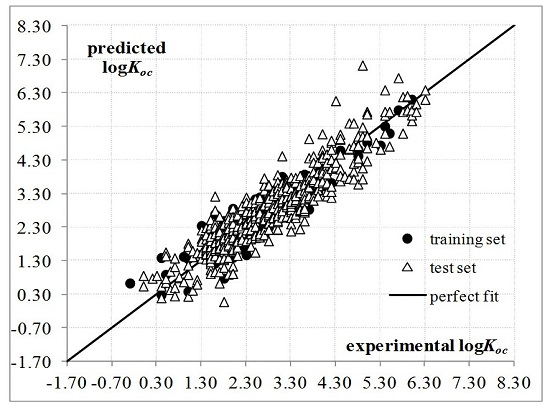
2. Results and Discussion
3. Materials and Methods
3.1. Experimental Dataset
3.2. Structural Representation and Molecular Descriptors Calculation
3.3. Model Development
3.3.1. Molecular Descriptors’ Selection in Multivariable Linear Regression (MLR)
3.3.2. The Optimal Molecular Descriptors
3.3.3. Model Validation
3.3.4. Applicability Domain
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sparks, D.L. Environmental Soil Chemistry; Academic Press: Tokyo, Japan, 2013; p. 267. [Google Scholar]
- Jury, W.A. Adsorption of organic chemicals onto soil. In Vadose Zone Modeling of Organic Pollutants; Henn, S.C., Melancon, S.M., Eds.; Lewis Publisher: New York, NY, USA, 1986; pp. 177–189. [Google Scholar]
- Gawlik, B.M.; Sotiriou, N.; Feicht, E.A.; Schulte-Hostede, S.; Kettrup, A. Alternatives for the determination of the soil adsorption coefficient, KOC, of non-ionic organic compounds—A review. Chemosphere 1997, 34, 2525–2551. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A. Exploring QSAR. Fundamentals and Applications in Chemistry and Biology; American Chemical Society: Washington, DC, USA, 1995. [Google Scholar]
- Kubinyi, H. QSAR: Hansch Analysis and Related Approaches; Wiley-Interscience: New York, NY, USA, 2008. [Google Scholar]
- Puzyn, T.; Leszczynski, J.; Cronin, M.T.D. Recent Advances in QSAR Studies: Methods and Applications; Springer Science & Business Media B.V.: Houten, The Netherlands, 2010. [Google Scholar]
- Katritzky, A.R.; Goordeva, E.V. Traditional topological indices vs. Electronic, geometrical, and combined molecular descriptors in QSAR/QSPR research. J. Chem. Inf. Comput. Sci. 1993, 33, 835–857. [Google Scholar] [CrossRef] [PubMed]
- Diudea, M.V.E. QSPR/QSAR Studies by Molecular Descriptors; Nova Science Publishers: New York, NY, USA, 2001. [Google Scholar]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics (Methods and Principles in Medicinal Chemistry); Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Sabljic, A.; Gusten, H.; Verhaar, H.; Hermens, J. QSAR modeling of soil sorption. Improvements and systematics of log Koc vs. Log kow correlations. Chemosphere 1995, 31, 4489–4514. [Google Scholar] [CrossRef]
- Duchowicz, P.R.; González, M.P.; Helguera, A.M.; Cordeiro, M.N.D.S.; Castro, E.A. Application of the replacement method as novel variable selection in QSPR. 2. Soil sorption coefficients. Chemom. Intell. Lab. Syst. 2007, 88, 197–203. [Google Scholar] [CrossRef]
- Goudarzi, N.; Goodarzi, M.; Araujo, M.C.U.; Galvão, R.K.H. QSPR modeling of soil sorption coefficients (Koc) of pesticides using SPA-ANN and SPA-MLR. J. Agric. Food Chem. 2009, 57, 7153–7158. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Liu, J.; Wanga, M.; Shi, L.; Yao, X.; Gramatica, P. Integrated QSPR models to predict the soil sorption coefficient for a large diverse set of compounds by using different modeling methods. Atmos. Environ. 2014, 88, 212–218. [Google Scholar] [CrossRef]
- Gramatica, P.; Giani, E.; Papa, E. Statistical external validation and consensus modeling: A QSPR case study for Koc prediction. J. Mol. Graph. Model. 2007, 25, 755–766. [Google Scholar] [CrossRef] [PubMed]
- Duchowicz, P.R.; Comelli, N.C.; Ortiz, E.V.; Castro, E.A. QSAR study for carcinogenicity in a large set of organic compounds. Curr. Drug Saf. 2012, 7, 282–288. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Toropova, A.P.; Benfenati, E.; Gini, G. OCWLGI descriptors: Theory and praxis. Curr. Comput. Aided Drug Des. 2013, 9, 226–232. [Google Scholar] [CrossRef] [PubMed]
- Ibezim, E.; Duchowicz, P.R.; Ortiz, E.V.; Castro, E.A. QSAR on aryl-piperazine derivatives with activity on malaria. Chemom. Intell. Lab. Syst. 2012, 110, 81–88. [Google Scholar] [CrossRef]
- Mullen, L.M.A.; Duchowicz, P.R.; Castro, E.A. QSAR treatment on a new class of triphenylmethyl-containing compounds as potent anticancer agents. Chemom. Intell. Lab. Syst. 2011, 107, 269–275. [Google Scholar] [CrossRef]
- Toropov, A.A.; Leszczynska, D.; Leszczynski, J. Predicting water solubility and octanol water partition coefficient for carbon nanotubes based on the chiral vector. Comput. Biol. Chem. 2007, 31, 127–128. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Toropova, A.P.; Benfenati, E.; Gini, G.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Novel application of the CORAL software to model cytotoxicity of metal oxide nanoparticles to bacteria Escherichia coli. Chemosphere 2012, 89, 1098–1102. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A.; Martyanov, S.E.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. CORAL: QSAR modeling of toxicity of organic chemicals towards Daphnia magna. Chemom. Intell. Lab. Syst. 2012, 110, 177–181. [Google Scholar] [CrossRef]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef]
- US EPA. Available online: https://www.epa.gov/tsca-screening-tools/epi-suitetm-estimation-program-interface (accessed on 29 July 2016).
- ACD/ChemSketch, 2016. Available online: http://www.acdlabs.com (accessed on 29 July 2016).
- PaDEL, 2016. Available online: http://www.yapcwsoft.com/ (accessed on 29 July 2016).
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef] [PubMed]
- Duchowicz, P.R.; Castro, E.A.; Fernández, F.M. Alternative algorithm for the search of an optimal set of descriptors in QSAR-QSPR studies. MATCH Commun. Math. Comput. Chem. 2006, 55, 179–192. [Google Scholar]
- Duchowicz, P.R.; Castro, E.A.; Fernández, F.M.; González, M. A new search algorithm of QSPR/QSAR theories: Normal boiling points of some organic molecules. Chem. Phys. Lett. 2005, 412, 376–380. [Google Scholar] [CrossRef]
- Duchowicz, P.R.; Talevi, A.; Bruno-Blanch, L.E.; Castro, E.A. New QSPR study for the prediction of aqueous solubility of drug-like compounds. Bioorg. Med. Chem. Lett. 2008, 16, 7944–7955. [Google Scholar] [CrossRef] [PubMed]
- Goodarzi, M.; Duchowicz, P.R.; Wu, C.H.; Fernández, F.M.; Castro, E.A. New hybrid genetic based support vector regression as QSAR approach for analyzing flavonoids-GABA(A) complexes. J. Chem. Inf. Model. 2009, 49, 1475–1485. [Google Scholar] [CrossRef] [PubMed]
- Pomilio, A.B.; Giraudo, M.A.; Duchowicz, P.R.; Castro, E.A. QSPR analyses for aminograms in food: Citrus juices and concentrates. Food. Chem. 2010, 123, 917–927. [Google Scholar] [CrossRef]
- Talevi, A.; Goodarzi, M.; Ortiz, E.V.; Duchowicz, P.R.; Bellera, C.L.; Pesce, G.; Castro, E.A.; Bruno-Blanch, L.E. Prediction of drug intestinal absorption by new linear and non-linear QSPR. Eur. J. Med. Chem. 2011, 46, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Pasquale, G.; Romanelli, G.P.; Autino, J.C.; García, J.; Ortiz, E.V.; Duchowicz, P.R. Quantitative structure-activity relationships on chalcone derivatives: Mosquito larvicidal studies. J. Agric. Food. Chem. 2012, 60, 692–697. [Google Scholar] [CrossRef] [PubMed]
- Matlab 7.0. Available online: http://www.mathworks.com (accessed on 29 July 2016).
- Coral 1.5. Available online: http://www.insilico.eu/coral (accessed on 29 July 2016).
- Wold, S.; Eriksson, L. Statistical validation of qsar results. In Chemometrics Methods in Molecular Design; van de Waterbeemd, H., Ed.; VCH: Weinheim, Germany, 1995; pp. 309–318. [Google Scholar]
- Gramatica, P. Principles of qsar models validation: Internal and external. QSAR Comb. Sci. 2007, 26, 694–701. [Google Scholar] [CrossRef]
- Eriksson, L.; Jaworska, J.; Worth, A.P.; Cronin, M.T.; McDowell, R.M.; Gramatica, P. Methods for reliability and uncertainty assessment and for applicability evaluations of classification- and regression-based QSARS. Environ. Health Perspect. 2003, 111, 1361–1375. [Google Scholar] [CrossRef] [PubMed]


| d | Descriptors | ||||
|---|---|---|---|---|---|
| 1 | CrippenLogP | 0.72 | 0.68 | 0.65 | 0.67 |
| 2 | CrippenLogP XLogP | 0.80 | 0.76 | 0.55 | 0.59 |
| 3 | CrippenLogP gmax TpiPC | 0.84 | 0.79 | 0.49 | 0.56 |
| 4 | SP3 CrippenLogP gmax XLogP | 0.87 | 0.81 | 0.45 | 0.53 |
| 5 | ALogp2 CrippenLogP maxHBint2 TpiPC XLogP | 0.87 | 0.81 | 0.44 | 0.52 |
| 6 | BCUTw-1l CrippenLogP gmax ETA_Epsilon_3 WPOL XLogP | 0.89 | 0.81 | 0.41 | 0.53 |
| Structural Attributes | |||||
|---|---|---|---|---|---|
| 0.84 | 0.73 | 0.49 | 0.64 | 50 | |
| 0.86 | 0.75 | 0.46 | 0.62 | 70 | |
| 0.87 | 0.76 | 0.45 | 0.61 | 64 |
| Structural Attribute | CW |
|---|---|
| EC0-O...1... | 0.12508 |
| EC0-C...3... | 1.00094 |
| EC0-H...1... | −0.18254 |
| EC0-H...1... | −0.18254 |
| NNC-O...101. | 0.24867 |
| NNC-C...303. | −0.75284 |
| NNC-H...101. | −0.07978 |
| NNC-H...101. | −0.07978 |
| NOSP01000000 | −0.74613 |
| d | Descriptors | ||||
|---|---|---|---|---|---|
| 1 | 0.77 | 0.76 | 0.59 | 0.59 | |
| 2 | MLFER_E | 0.86 | 0.83 | 0.46 | 0.50 |
| 3 | MLFER_E SubFP302 | 0.87 | 0.84 | 0.44 | 0.48 |
| 4 | mindO MLFER_E KRFP1105 | 0.88 | 0.84 | 0.42 | 0.48 |
| 5 | MAXDP2 ZMIC1 TpiPC KRFP3788 | 0.90 | 0.84 | 0.40 | 0.49 |
| 6 | ATSC3c AATSC3c MATS4p MLFER_E AD2D393 | 0.91 | 0.84 | 0.37 | 0.49 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aranda, J.F.; Garro Martinez, J.C.; Castro, E.A.; Duchowicz, P.R. Conformation-Independent QSPR Approach for the Soil Sorption Coefficient of Heterogeneous Compounds. Int. J. Mol. Sci. 2016, 17, 1247. https://doi.org/10.3390/ijms17081247
Aranda JF, Garro Martinez JC, Castro EA, Duchowicz PR. Conformation-Independent QSPR Approach for the Soil Sorption Coefficient of Heterogeneous Compounds. International Journal of Molecular Sciences. 2016; 17(8):1247. https://doi.org/10.3390/ijms17081247
Chicago/Turabian StyleAranda, José F., Juan C. Garro Martinez, Eduardo A. Castro, and Pablo R. Duchowicz. 2016. "Conformation-Independent QSPR Approach for the Soil Sorption Coefficient of Heterogeneous Compounds" International Journal of Molecular Sciences 17, no. 8: 1247. https://doi.org/10.3390/ijms17081247
APA StyleAranda, J. F., Garro Martinez, J. C., Castro, E. A., & Duchowicz, P. R. (2016). Conformation-Independent QSPR Approach for the Soil Sorption Coefficient of Heterogeneous Compounds. International Journal of Molecular Sciences, 17(8), 1247. https://doi.org/10.3390/ijms17081247