Large-Scale Simulation of the Phenotypical Variability Induced by Loss-of-Function Long QT Mutations in Human Induced Pluripotent Stem Cell Cardiomyocytes
Abstract
:1. Introduction
2. Results
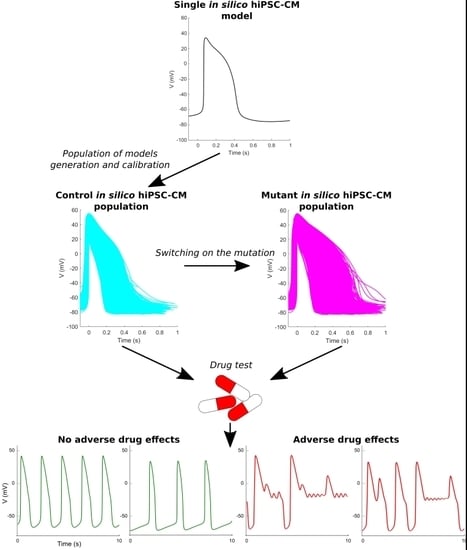
2.1. The Control and the Mutant LQT1 Populations
2.2. The Control and the Mutant LQT2 Populations
2.3. At Risk vs. Normal-Like Mutant hiPSC-CMs
2.4. Quinidine Effect on hiPSC-CMs
3. Discussion
4. Materials and Methods
4.1. General Approach and Study Design
4.2. Control and Mutant Slow Delayed Rectifying Current IKs
4.3. Control and Mutant Rapid Delayed Rectifying Current IKr
4.4. Control Populations (LQT1_CTRL and LQT2_CTRL) of In Silico hiPSC-CMs
4.5. Mutant LQT1 and LQT2 (LQT1_MUT and LQT2_MUT) In Silico Populations
4.6. In Silico Drug Tests
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AP | Action potential |
| APDxx | Action potential duration at xx% |
| hiPSC | Human induced pluripotent stem cell |
| APA | Action potential amplitude |
| DAD | Delayed afterdepolarization |
| dV/dtmax | Maximum upstroke velocity |
| EAD | Early afterdepolarization |
| EHT | Engineered heart tissue |
| FDA | Food and drug administration |
| hiPSC-CM | Human induced pluripotent stem cell-derived cardiomyocyte |
| ICaL | L-type Ca2+ current |
| If | Funny current |
| IKr | Rapid delayed rectifying K+ current |
| IKs | Slow delayed rectifying K+ current |
| IK1 | Inward rectifying K+ current |
| INa | Fast Na+ current |
| INaK | Na+/K+ pump |
| INaL | Late Na+ current |
| INCX | Na+/Ca2+ exchanger |
| IpCa | Sarcolemmal Ca2+ pump |
| IRyR | RyR-sensitive Ca2+ release |
| ISERCA | SERCA pump |
| Ito | Transient outward K+ current |
| LB | Lower bound |
| LQT1_CTRL | hiPSC-CM population with control IKs from [3] |
| LQT1_MUT | hiPSC-CM population with mutant IKs from [3] |
| LQT2_CTRL | hiPSC-CM population with control IKr from [4] |
| LQT2_MUT | hiPSC-CM population with mutant IKr from [4] |
| MDP | Maximum diastolic potential |
| mean | Mean value |
| Paci2018 | hiPSC-CM model from [20] |
| Peak | Peak potential |
| Rate | Spontaneous action potential rate |
| SD | Standard deviation |
| UB | Upper bound |
| ΔAPD90% | Percent APD90 variation |
References
- Rodriguez, B.; Carusi, A.; Abi-Gerges, N.; Ariga, R.; Britton, O.; Bub, G.; Bueno-Orovio, A.; Burton, R.A.B.; Carapella, V.; Cardone-Noott, L.; et al. Human-based approaches to pharmacology and cardiology: An interdisciplinary and intersectorial workshop. Europace 2016, 18, 1287–1298. [Google Scholar] [CrossRef] [PubMed]
- Colatsky, T.; Fermini, B.; Gintant, G.; Pierson, J.B.; Sager, P.; Sekino, Y.; Strauss, D.G.; Stockbridge, N. The Comprehensive in Vitro Proarrhythmia Assay (CiPA) initiative—Update on progress. J. Pharmacol. Toxicol. Methods 2016, 81, 15–20. [Google Scholar] [CrossRef] [PubMed]
- Moretti, A.; Bellin, M.; Welling, A.; Jung, C.B.; Lam, J.T.; Bott-Flügel, L.; Dorn, T.; Goedel, A.; Höhnke, C.; Hofmann, F.; et al. Patient-specific induced pluripotent stem-cell models for long-QT syndrome. N. Engl. J. Med. 2010, 363, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Bellin, M.; Casini, S.; Davis, R.P.; D’Aniello, C.; Haas, J.; Ward-van Oostwaard, D.; Tertoolen, L.G.J.; Jung, C.B.; Elliott, D.A.; Welling, A.; et al. Isogenic human pluripotent stem cell pairs reveal the role of a KCNH2 mutation in long-QT syndrome. EMBO J. 2013, 32, 3161–3175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lahti, A.L.; Kujala, V.J.; Chapman, H.; Koivisto, A.-P.; Pekkanen-Mattila, M.; Kerkela, E.; Hyttinen, J.; Kontula, K.; Swan, H.; Conklin, B.R.; et al. Model for long QT syndrome type 2 using human iPS cells demonstrates arrhythmogenic characteristics in cell culture. Dis. Model. Mech. 2012, 5, 220–230. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Wei, H.; Zhao, Y.; Lu, J.; Li, G.; Binte, N.; Sahib, E.; Hong, T.; Yean, K.; Shim, W.; et al. Modeling type 3 long QT syndrome with cardiomyocytes derived from patient-specific induced pluripotent stem cells. Int. J. Cardiol. 2013, 168, 5277–5286. [Google Scholar] [CrossRef] [PubMed]
- Rocchetti, M.; Sala, L.; Dreizehnter, L.; Crotti, L.; Sinnecker, D.; Mura, M.; Pane, L.S.; Altomare, C.; Torre, E.; Mostacciuolo, G.; et al. Elucidating arrhythmogenic mechanisms of long-QT syndrome CALM1-F142L mutation in patient-specific induced pluripotent stem cell-derived cardiomyocytes. Cardiovasc. Res. 2017, 113, 531–541. [Google Scholar] [CrossRef] [PubMed]
- Kujala, K.; Paavola, J.; Lahti, A.; Larsson, K.; Pekkanen-Mattila, M.; Viitasalo, M.; Lahtinen, A.M.; Toivonen, L.; Kontula, K.; Swan, H.; et al. Cell model of catecholaminergic polymorphic ventricular tachycardia reveals early and delayed afterdepolarizations. PLoS ONE 2012, 7, e44660. [Google Scholar] [CrossRef] [PubMed]
- Ojala, M.; Prajapati, C.; Pölönen, R.P.; Rajala, K.; Pekkanen-Mattila, M.; Rasku, J.; Larsson, K.; Aalto-Setälä, K. Mutation-specific phenotypes in hiPSC-derived cardiomyocytes carrying either myosin-binding protein C or alfa-tropomyosin mutation for hypertrophic cardiomyopathy. Stem Cells Int. 2016, 2016. [Google Scholar] [CrossRef] [PubMed]
- Davis, R.P.; Casini, S.; van den Berg, C.W.; Hoekstra, M.; Remme, C.A.; Dambrot, C.; Salvatori, D.; Oostwaard, D.W.; Wilde, A.A.M.; Bezzina, C.R.; et al. Cardiomyocytes derived from pluripotent stem cells recapitulate electrophysiological characteristics of an overlap syndrome of cardiac sodium channel disease. Circulation 2012, 125, 3079–3091. [Google Scholar] [CrossRef] [PubMed]
- Paci, M.; Hyttinen, J.; Aalto-Setälä, K.; Severi, S. Computational models of ventricular- and atrial-like human induced pluripotent stem cell derived cardiomyocytes. Ann. Biomed. Eng. 2013, 41, 2334–2348. [Google Scholar] [CrossRef] [PubMed]
- Paci, M.; Sartiani, L.; Lungo, M.; Jaconi, M.; Mugelli, A.; Cerbai, E.; Severi, S. Mathematical modelling of the action potential of human embryonic stem cell derived cardiomyocytes. Biomed. Eng. Online 2012, 11, 61. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, J.; Guo, L.; Fiene, S.J.; Anson, B.D.; Thomson, J.A.; Kamp, T.J.; Kolaja, K.L.; Swanson, B.J.; January, C.T. High purity human-induced pluripotent stem cell-derived cardiomyocytes: Electrophysiological properties of action potentials and ionic currents. AJP Hear. Circ. Physiol. 2011, 301, H2006–H2017. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.; Chang, K.C.; Beattie, K.A.; Sheng, J.; Tran, P.N.; Wu, W.W.; Wu, M.; Strauss, D.G.; Colatsky, T.; Li, Z. Optimization of an in silico cardiac cell model for proarrhythmia risk assessment. Front. Physiol. 2017, 8, 1–15. [Google Scholar] [CrossRef]
- Paci, M.; Hyttinen, J.; Rodriguez, B.; Severi, S. Human induced pluripotent stem cell-derived versus adult cardiomyocytes: An in silico electrophysiological study on effects of ionic current block. Br. J. Pharmacol. 2015, 172, 5147–5160. [Google Scholar] [CrossRef] [PubMed]
- Knollmann, B.C. Induced pluripotent stem cell-derived cardiomyocytes: Boutique science or valuable arrhythmia model? Circ. Res. 2013, 112, 969–976. [Google Scholar] [CrossRef] [PubMed]
- Britton, O.J.; Bueno-Orovio, A.; Van Ammel, K.; Lu, H.R.; Towart, R.; Gallacher, D.J.; Rodriguez, B. Experimentally calibrated population of models predicts and explains intersubject variability in cardiac cellular electrophysiology. Proc. Natl. Acad. Sci. USA 2013, 110, E2098–E2105. [Google Scholar] [CrossRef] [PubMed]
- Paci, M.; Passini, E.; Severi, S.; Hyttinen, J.; Rodriguez, B. Phenotypic variability in LQT3 human induced pluripotent stem cell-derived cardiomyocytes and their response to antiarrhythmic pharmacologic therapy: An in silico approach. Hear. Rhythm 2017, 14, 1704–1712. [Google Scholar] [CrossRef] [PubMed]
- Passini, E.; Britton, O.J.; Lu, H.R.; Rohrbacher, J.; Hermans, A.N.; Gallacher, D.J.; Greig, R.J.H.; Bueno-Orovio, A.; Rodriguez, B. Human In Silico Drug Trials Demonstrate Higher Accuracy than Animal Models in Predicting Clinical Pro-Arrhythmic Cardiotoxicity. Front. Physiol. 2017, 8, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Paci, M.; Pölönen, R.-P.; Cori, D.; Penttinen, K.; Aalto-Setälä, K.; Severi, S.; Hyttinen, J. Automatic optimization of an in silico model of human iPSC derived cardiomyocytes recapitulating calcium handling abnormalities. Front. Physiol. 2018, 9, 709. [Google Scholar] [CrossRef] [PubMed]
- Morita, H.; Wu, J.; Zipes, D.P. The QT syndromes: Long and short. Lancet 2008, 372, 750–763. [Google Scholar] [CrossRef]
- Varró, A.; Baczkó, I. Cardiac ventricular repolarization reserve: A principle for understanding drug-related proarrhythmic risk. Br. J. Pharmacol. 2011, 164, 14–36. [Google Scholar] [CrossRef] [PubMed]
- Roden, D.M. Editorial: Repolarization reserve: A moving target. Circulation 2008, 118, 981–982. [Google Scholar] [CrossRef] [PubMed]
- Lemoine, M.D.; Krause, T.; Koivumäki, J.T.; Prondzynski, M.; Schulze, M.L.; Girdauskas, E.; Willems, S.; Hansen, A.; Eschenhagen, T.; et al. Human Induced Pluripotent Stem Cell–Derived Engineered Heart Tissue as a Sensitive Test System for QT Prolongation and Arrhythmic Triggers. Circ. Arrhythmia Electrophysiol. 2018, 11, e006035. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; D’Aniello, C.; Verkerk, A.O.; Wrobel, E.; Frank, S.; Ward-van Oostwaard, D.; Piccini, I.; Freund, C.; Rao, J.; Seebohm, G.; et al. Recessive cardiac phenotypes in induced pluripotent stem cell models of Jervell and Lange-Nielsen syndrome: Disease mechanisms and pharmacological rescue. Proc. Natl. Acad. Sci. USA 2014, 111, E5383–E5392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Christ, T.; Horvath, A.; Eschenhagen, T. LQT1-phenotypes in hiPSC: Are we measuring the right thing? Proc. Natl. Acad. Sci. USA 2015, 112, E1968. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Xian, W.; Bellin, M.; Dorn, T.; Tian, Q.; Goedel, A.; Dreizehnter, L.; Schneider, C.M.; Ward-Van Oostwaard, D.; Ng, J.K.M.; et al. Subtype-specific promoter-driven action potential imaging for precise disease modelling and drug testing in hiPSC-derived cardiomyocytes. Eur. Heart J. 2017, 38, 292–301. [Google Scholar] [CrossRef] [PubMed]
- Passini, E.; Mincholé, A.; Coppini, R.; Cerbai, E.; Rodriguez, B.; Severi, S.; Bueno-Orovio, A. Mechanisms of pro-arrhythmic abnormalities in ventricular repolarisation and anti-arrhythmic therapies in human hypertrophic cardiomyopathy. J. Mol. Cell. Cardiol. 2016, 96, 72–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krogh-Madsen, T.; Jacobson, A.F.; Ortega, F.A.; Christini, D.J. Global optimization of ventricular myocyte model to multi-variable objective improves predictions of drug-induced Torsades de Pointes. Front. Physiol. 2017, 8, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Kuusela, J.; Kujala, V.J.; Kiviaho, A.; Ojala, M.; Swan, H.; Kontula, K.; Aalto-Setälä, K. Effects of cardioactive drugs on human induced pluripotent stem cell derived long QT syndrome cardiomyocytes. Springerplus 2016, 5, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Woosley, R.; Heise, C.; Romero, K. CredibleMeds, QTdrugs List. Available online: https://crediblemeds.org/ (accessed on 28 August 2018).
- Casini, S.; Verkerk, A.O.; Remme, C.A. Human iPSC-Derived Cardiomyocytes for Investigation of Disease Mechanisms and Therapeutic Strategies in Inherited Arrhythmia Syndromes: Strengths and Limitations. Cardiovasc. Drugs Ther. 2017, 31, 325–344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paci, M.; Passini, E.; Severi, S.; Hyttinen, J.; Rodriguez, B. A population of in silico models to face the variability of human induced pluripotent stem cell-derived cardiomyocytes: The hERG block case study. In Proceedings of the 2016 Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 1189–1192. [Google Scholar]
- Ten Tusscher, K.H.W.J.; Noble, D.; Noble, P.J.; Panfilov, A. V A model for human ventricular tissue. Am. J. Physiol. Hear. Circ. Physiol. 2004, 286, H1573–H1589. [Google Scholar] [CrossRef] [PubMed]
- Fatima, A.; Kaifeng, S.; Dittmann, S.; Xu, G.; Gupta, M.K.; Linke, M.; Zechner, U.; Nguemo, F.; Milting, H.; Farr, M.; et al. The disease-specific phenotype in cardiomyocytes derived from induced pluripotent stem cells of two long QT syndrome type 3 patients. PLoS ONE 2013, 8, e83005. [Google Scholar] [CrossRef] [PubMed]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; Wiley-Interscience: New York, NY, USA, 2000; ISBN 978-0-471-05669-0. [Google Scholar]
- Kramer, J.; Obejero-Paz, C.A.; Myatt, G.; Kuryshev, Y.A.; Bruening-Wright, A.; Verducci, J.S.; Brown, A.M. MICE models: Superior to the HERG model in predicting Torsade de Pointes. Sci. Rep. 2013, 3, 2100. [Google Scholar] [CrossRef] [PubMed]
- Crumb, W.J.; Vicente, J.; Johannesen, L.; Strauss, D.G. An evaluation of 30 clinical drugs against the comprehensive in vitro proarrhythmia assay (CiPA) proposed ion channel panel. J. Pharmacol. Toxicol. Methods 2016. [Google Scholar] [CrossRef] [PubMed]
- Strauss, D.G.; Gintant, G.; Li, Z.; Wu, W.; Blinova, K.; Vicente, J.; Turner, J.R.; Sager, P.T. Comprehensive In Vitro Proarrhythmia Assay (CiPA) Update from a Cardiac Safety Research Consortium/Health and Environmental Sciences Institute/FDA Meeting. Ther. Innov. Regul. Sci. 2018. [Google Scholar] [CrossRef] [PubMed]















| Population (# Models) | Rate (bpm) | MDP (mV) | Peak (mV) | APA (mV) | dV/dtmax (V/s) | APD50 (ms) | APD90 (ms) |
|---|---|---|---|---|---|---|---|
| LQT1_CTRL (3584) | 46 ± 15 | −77 ± 3 | 38 ± 7 | 114 ± 9 | 37 ± 21 | 274 ± 63 | 344 ± 74 |
| LQT1_MUT (3238) | 44 ± 14 | −77 ± 3 | 38 ± 7 | 114 ± 9 | 36 ± 21 | 317 ± 94 | 389 ± 102 |
| LQT2_CTRL spontaneous (1226) | 45 ± 14 | −76 ± 3 | 35 ± 5 | 111 ± 7 | 40 ± 21 | 209 ± 55 | 254 ± 63 |
| LQT2_MUT spontaneous (1008) | 40 ± 12 | −77 ± 3 | 40 ± 4 | 116 ± 6 | 41 ± 21 | 292 ± 58 | 340 ± 64 |
| LQT2_CTRL paced (979) | 60 ± 0 | −76 ± 3 | 37 ± 5 | 114 ± 7 | 55 ± 24 | 233 ± 60 | 288 ± 72 |
| LQT2_MUT paced (650) | 60 ± 0 | −76 ± 3 | 42 ± 4 | 118 ± 5 | 52 ± 23 | 322 ± 62 | 380 ± 70 |
| AP Biomarkers | Moretti 2010 [3] Control (n = 21) | Moretti 2010 [3] Mutant (n = 14) |
|---|---|---|
| Rate (bpm) | 68 ± 12 | 60 ± 8 |
| MDP (mV) | −64 ± 10 | −65 ± 10 |
| Peak (mV) | 44 ± 7 | 46 ± 8 |
| APA (mV) | 108 ± 10 | 110 ± 10 |
| dV/dtmax (V/s) | 9 ± 1 | 8 ± 1 |
| APD50 (ms) | 323 ± 139 | 654 ± 328 |
| APD90 (ms) | 381 ± 162 | 745 ± 342 |
| AP biomarkers | Bellin 2013 [4] Control (n = 10) | Bellin 2013 [4] Mutant (n = 14) |
|---|---|---|
| Rate (bpm) | 60 ± 0 | 60 ± 0 |
| MDP (mV) | −75 ± 6 | −75 ± 6 |
| APA (mV) | 116 ± 10 | 120 ± 9 |
| dV/dtmax (V/s) | 71 ± 39 | 66 ± 42 |
| APD50 (ms) | 164 ± 78 | 227 ± 66 |
| APD90 (ms) | 207 ± 92 | 292 ± 81 |
| Dose (µM) | LQT1_CTRL | LQT1_MUT (at Risk vs. Normal-Like) | LQT2_CTRL | LQT2_MUT (at Risk vs. Normal-Like) |
|---|---|---|---|---|
| 0 | 0% | 0% (0% vs. 0%) | 0% | 0% (0% vs. 0%) |
| 1.5 | 5% | 11% (16% vs. 7%) | 1% | 1% (2% vs. 0%) |
| 3 | 11% | 23% (29% vs. 18%) | 4% | 6% (10% vs. 4%) |
| 9 | 35% | 54% (55% vs. 53%) | 46% | 46% (50% vs. 44%) |
| Dataset (# Cells) | Ma2011 [13] (32) | Moretti2010 [3] (21) | Ma2013 [6] (12) | Fatima2013 [35] (6) | Lahti2012 [5] (13) | Kujala2012 [8] (16) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AP biomarkers | LB | UB | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD |
| Rate (bpm) | >0 | 209 | 35 | 12 | 68 | 12 | 69 | 39 | 118 | 45 | 72 | 22 | 41 | 24 |
| MDP (mV) | −89 | −44 | −76 | 7 | −64 | 10 | −61 | 5 | −64 | 6 | −63 | 5 | −68 | 7 |
| Peak (mV) | 17 | 58 | 28 | 6 | 44 | 7 | --- | --- | 39 | 3 | --- | --- | --- | --- |
| APA (mV) | 76 | 139 | 104 | 6 | 108 | 10 | 86 | 5 | 102 | 5 | 113 | 9 | 118 | 10 |
| dV/dtmax (V/s) | >0 | 82 | 28 | 27 | 9 | 1 | 13 | 16 | 24 | 12 | 27 | 23 | --- | --- |
| APD10 (ms) | 20 | 128 | 74 | 27 | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| APD20 (ms) | >0 | 290 | --- | --- | --- | --- | 138 | 76 | --- | --- | --- | --- | --- | --- |
| APD30 (ms) | 59 | 301 | 180 | 61 | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| APD50 (ms) | >0 | 601 | --- | --- | 323 | 139 | 338 | 115 | 175 | 106 | 265 | 54 | 204 | 81 |
| APD70 (ms) | 146 | 631 | --- | --- | --- | --- | 388 | 121 | --- | --- | --- | --- | --- | --- |
| APD90 (ms) | 1 | 705 | 415 | 123 | 381 | 162 | 434 | 108 | 298 | 148 | 314 | 63 | 330 | 90 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paci, M.; Casini, S.; Bellin, M.; Hyttinen, J.; Severi, S. Large-Scale Simulation of the Phenotypical Variability Induced by Loss-of-Function Long QT Mutations in Human Induced Pluripotent Stem Cell Cardiomyocytes. Int. J. Mol. Sci. 2018, 19, 3583. https://doi.org/10.3390/ijms19113583
Paci M, Casini S, Bellin M, Hyttinen J, Severi S. Large-Scale Simulation of the Phenotypical Variability Induced by Loss-of-Function Long QT Mutations in Human Induced Pluripotent Stem Cell Cardiomyocytes. International Journal of Molecular Sciences. 2018; 19(11):3583. https://doi.org/10.3390/ijms19113583
Chicago/Turabian StylePaci, Michelangelo, Simona Casini, Milena Bellin, Jari Hyttinen, and Stefano Severi. 2018. "Large-Scale Simulation of the Phenotypical Variability Induced by Loss-of-Function Long QT Mutations in Human Induced Pluripotent Stem Cell Cardiomyocytes" International Journal of Molecular Sciences 19, no. 11: 3583. https://doi.org/10.3390/ijms19113583
APA StylePaci, M., Casini, S., Bellin, M., Hyttinen, J., & Severi, S. (2018). Large-Scale Simulation of the Phenotypical Variability Induced by Loss-of-Function Long QT Mutations in Human Induced Pluripotent Stem Cell Cardiomyocytes. International Journal of Molecular Sciences, 19(11), 3583. https://doi.org/10.3390/ijms19113583