Systems Approach to Study Associations between OxLDL and Abdominal Aortic Aneurysms
Abstract
:1. Introduction
2. Analysis
- AvgF for in full model is 19.40, while AvgF for in full model with knockout of is 19.46.
- AvgF for in full model is 4.85, while AvgF for in full model with knockout of is 4.86.
3. Petri-Net-Based Models
4. Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Proposed Petri Net Model
| Place | Biological Meaning | Place | Biological Meaning |
|---|---|---|---|
| superoxide anion radical | PKC | ||
| oxidized LDL | NFB | ||
| LDL | chemokines | ||
| NO | inflammatory cytokines | ||
| peroxynitrite | MMPs | ||
| BH | adhesion particles | ||
| NOSs | circulating inflammatory cells | ||
| BH | TNF | ||
| HO | p38MAPK | ||
| ROS | active inflammatory cells | ||
| dismutase | hemodynamic stress | ||
| catalase | COX2 | ||
| NOX | PGE2 | ||
| ANGII | less elastin | ||
| ANGI | less collagen | ||
| ACE | enlarged AAA | ||
| tyrosine kinase | deposited collagen | ||
| PARP polymerase | HOCl | ||
| AP1 | MPO | ||
| Akt | IL-6 |
| Transition | Biological Meaning | Transition | Biological Meaning |
|---|---|---|---|
| LDL oxidation | expression of MMPs by inflammatory cytokines | ||
| blood as LDL source | activation of MMPs by ROS | ||
| peroxynitrite synthesis | production of adhesion particles | ||
| BH synthesis | diapedesis | ||
| NO synthesis | source of inflammatory cells | ||
| NOSs sources | source of ANGI | ||
| BH oxidation to BH through peroxynitrite | elastine proteolysis by MMPs | ||
| BH oxidation to BH through O | source of TNF | ||
| O synthesis via NOSs and BH | pool of inflamatory cytokines | ||
| pool of ROS | activation of p38MAPK | ||
| dismutation | production of inflammatory cytokines by inflmmatory cells | ||
| source of dismutase | direct stimulation of NFB via ANGII | ||
| HO reduction | O synthesis via NOSs and oxLDL | ||
| source of catalase | stimulation of adhesion particles | ||
| O synthesis through NOX | stimulation of NFB by TNF | ||
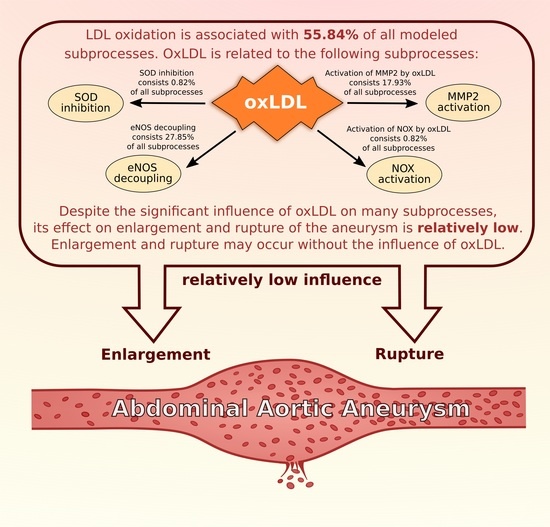
| indirect stimulation of NOX through oxLDL | activation of NOX by hemodynamic stress | ||
| activation of NOX through TNF | activation of COX2 by hemodynamic stress | ||
| activation of NOX by ANGII | production of PGE2 by COX2 | ||
| conversion of ANGI to ANGII | activation of NFB via PGE2 | ||
| source of ACE | collagen proteolysis by MMPs | ||
| activation of ACE by ROS | enlargement of AAA | ||
| stimulation of tyrosine kinase | compensating collagen deposition | ||
| DNA damage and release of PARP | rupture of AAA | ||
| stimulation of AP1 | degradation of chemokines | ||
| indirect stimulation of Akt | additional activation of elastin proteolysis by MMP2 | ||
| VSMC apoptosis | increase of hemodynamic stress | ||
| stimulation of PKC by PARP | activation of iNOS by inflammatory cytokines | ||
| activation of NFB by PKC | inhibition of SOD | ||
| stimulation of inflammatory cytokines production by AP1 | production of HOCl by MPO | ||
| stimulation of inflammatory cytokines production by NFB | source of MPO | ||
| stimulation of chemokines production by AP1 | activation of MMPs by HOCl | ||
| stimulation of chemokines production by NFB | stimulation of IL-6 |

Appendix B. Analysis of MCT Sets
| MCT-Set | Contained Transitions | Biological Meaning |
|---|---|---|
| , , | Oxidation of BH to BH by ONOO. | |
| , , | Dismutation of NOX-derived O. | |
| , , | Apoptosis of VSMC. | |
| , , | Activation of NFB caused by DNA damage by ROS. | |
| , , | Infiltration by inflammatory cells. | |
| , , | Activation of NFB via PGE2 activated by COX2. | |
| , , | Collagen proteolysis and rupture of aneurysm. | |
| , | Oxidation of LDL. | |
| , | Synthesis of O by NOS and BH. | |
| , | Reduction of HO by catalase. | |
| , | Conversion of ANGI to ANGII by ACE. | |
| , | Stimulation of AP1 by ROS. | |
| , | Stimulation of IL-6 by hemodynamic stress. | |
| , | Influence of aneurysm enlargement on hemodynamic stress. | |
| , | Production of HOCl by MPO and HO. |
Appendix C. Analysis of t-Clusters
| t-Cluster | Biological Meaning |
|---|---|
| Uncoupling of NOS by ONOO and O. | |
| Influence of hemodynamic stress on activation of NFB, which activates production of chemokines and inflammatory cytokines, and results in inflammatory cells infiltration. Inflammatory state leads to production of MMPs and enlargement of aneurysm. | |
| This cluster includes all modeled subprocesses. | |
| This cluster includes almost all modeled subprocesses except: activation of NOX through TNF. | |
| Activation of NFB by TNF. NFB produces chemokines. | |
| Influence of ANGII on enlargement and rupture of aneurysm. | |
| Synthesis of HOCL by MPO leads to activation of MMPs which results in enlargement and rupture of aneurysm. Activation of NOX by ANGII, TNF, hemodynamic stress. PGE2 stimulates NFB which activates production of chemokines. | |
| Activation of inflammatory cytokines (TNF and IL-6) resulting in enlargement of aneurysm. | |
This cluster includes almost all modeled subprocesses except:
| |
| Activation of NFB by TNF. NFB produces cytokines, which activates iNOS. iNOS and eNOS are uncoupled by ONOO and O. | |
| Activation of NFB by ANGII. NFB activates production of chemokines and inflammatory cytokines, and results in inflammatory cells infiltration. Cytokines activates iNOS, iNOS and eNOS are uncoupled by ONOO and O. | |
| Activation of NOX by ANGII and TNF. PGE2 stimulates NFB, which enhances tissue infiltration by inflammatory cells. Inflammatory cells produce cytokines resulting in activation of iNOS. Part of O undergoes dismutation to HO, and other part reacts with NO leading to ONOO synthesis. ONOO leads to uncoupling of NOS. Synthesis of HOCL by MPO leads to activation of MMPs which results in enlargement of aneurysm. | |
| Activation of NOX by ANGII, TNF and hemodynamic stress. ANGII and TNF stimulates NFB, which enhances tissue infiltration by inflammatory cells. Inflammatory cells produce cytokines (mainly IL-6, IL-1 and TNF) resulting in activation of iNOS. Part of O undergoes dismutation to HO, and other part reacts with NO leading to ONOO synthesis. ONOO leads to uncoupling of NOS. Synthesis of HOCl by MPO leads to activation of MMPs which results in enlargement and rupture of aneurysm. | |
| Activation of NFB by TNF. NFB activates production of chemokines and adhesion particles, which results in inflammatory cells infiltration. Cytokines activates iNOS, iNOS and eNOS are uncoupled by ONOO. | |
| Activation of NFB by ANGII and TNF. TNF and IL-6 as inflammatory cytokines lead to expression of MMPs and enlargement of aneurysm. Adhesion particles produced by NFB and chemokines result in inflammatory cells infiltration. Cytokines activates iNOS, iNOS and eNOS are uncoupled by ONOO. | |
| Activation of NFB by TNF leads to inflammatory cytokines production. Inflammatory cytokines activates expression of MMPs, which results in enlargement and rupture of aneurysm. | |
This cluster includes almost all modeled subprocesses except:
|
References
- Newby, D.; Forsythe, R.; McBride, O. Aortic Wall Inflammation Predicts Abdominal Aortic Aneurysm Expansion, Rupture, and Need for Surgical Repair. Circulation 2017, 136, 787–797. [Google Scholar] [CrossRef]
- Toghill, B.J.; Saratzis, A.; Bown, M.J. Abdominal aortic aneurysm-an independent disease to atherosclerosis? Cardiovasc. Pathol. 2017, 27, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Guzik, B. Rola Anionu Ponadtlenkowego w Etiopatogenezie Tętniaków Aorty Brzusznej. Ph.D. Dissertation, Institute of Cardiology, Jagiellonian University Collegium Medicum, Krakow, Poland, 2006. [Google Scholar]
- Golledge, J.; Norman, P. Atherosclerosis and abdominal aortic aneurysm: Cause, response or common risk factors? Arterioscler. Thromb. Vasc. Biol. 2010, 30, 1075–1077. [Google Scholar] [CrossRef] [PubMed]
- Trollope, A.F.; Golledge, J. Angiopoietins, abdominal aortic aneurysm and atherosclerosis. Atherosclerosis 2011, 214, 237–243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuivaniemi, H.; Ryer, E.J.; Elmore, J.R.; Tromp, G. Understanding the pathogenesis of abdominal aortic aneurysms. Expert Rev. Cardiovasc. Ther. 2015, 13, 975–987. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yansheng, Y.; Yanbing, W.; Yibo, Z.; Chang, L. Klotho ameliorates oxidized low density lipoprotein (ox-LDL)-induced oxidative stress via regulating LOX-1 and PI3K/Akt/eNOS pathways. Lipids Health Dis. 2017, 16, 77. [Google Scholar] [CrossRef]
- Kubota, Y.; Folsom, A.R.; Ballantyne, C.M.; Tang, W. Lipoprotein(a) and abdominal aortic aneurysm risk: The Atherosclerosis Risk in Communities study. Atherosclerosis 2018, 268, 63–67. [Google Scholar] [CrossRef]
- Li, W.; Luo, S.; Luo, J.; Liu, Y.; Ning, B.; Huang, W.; Xue, L.; Chen, J. Predictors Associated With Increased Prevalence of Abdominal AorticAneurysm in Chinese Patients with Atherosclerotic Risk Factors. Eur. J. Vasc. Endovasc. Surg. 2017, 54, 43–49. [Google Scholar] [CrossRef]
- Hobbs, S.D.; Claridge, M.W.; Quick, C.R.; Day, N.E.; Bradbury, A.W.; Wilmink, A.B. LDL cholesterol is associated with small abdominal aortic aneurysms. Eur. J. Vasc. Endovasc. Surg. 2003, 26, 618–622. [Google Scholar] [CrossRef]
- Liu, J.; Lu, H.; Howatt, D.A.; Balakrishnan, A.; Moorleghen, J.J.; Sorci-Thomas, M.; Cassis, L.A.; Daugherty, A. Associations of ApoAI and ApoB-containing lipoproteins with AngII-induced abdominal aortic aneurysms in mice. Arterioscler. Thromb. Vasc. Biol. 2015, 35, 1826–1834. [Google Scholar] [CrossRef]
- Prins, P.A.; Hill, M.F.; Airey, D.; Nwosu, S.; Perati, P.R.; Tavori, H.; Linton, M.F.; Kon, V.; Fazio, S.; Sampson, U.K. Angiotensin-induced abdominal aortic aneurysms in hypercholesterolemic mice: Role of serum cholesterol and temporal effects of exposure. PLoS ONE 2014, 9, e84517. [Google Scholar] [CrossRef] [PubMed]
- Frösen, J.; Tulamo, R.; Heikura, T.; Sammalkorpi, S.; Niemelä, M.; Hernesniemi, J.; Levonen, A.L.; Hörkkö, S.; Ylä-Herttuala, S. Lipid accumulation, lipid oxidation, and low plasma levels of acquired antibodies against oxidized lipids associate with degeneration and rupture of the intracranial aneurysm wall. Acta Neuropathol. Commun. 2013, 1, 71. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Siu, K.L.; Chalupsky, K.; Nguyen, A.; Chen, P.; Weintraub, N.L.; Galis, Z.; Cai, H. Role of uncoupled endothelial nitric oxide synthase in abdominal aortic aneurysm formation: Treatment with folic acid. Hypertension 2012, 59, 158–166. [Google Scholar] [CrossRef] [PubMed]
- Muller, G.; Morawietz, H. Nitric oxide, NAD(P)H oxidase, and atherosclerosis. Antioxid. Redox Signal. 2009, 11, 1711–1731. [Google Scholar] [CrossRef] [PubMed]
- Schulz, E.; Gori, T.; Münzel, T. Oxidative stress and endothelial dysfunction in hypertension. Hypertens. Res. 2011, 34, 665–673. [Google Scholar] [CrossRef] [PubMed]
- McCormick, M.L.; Gavrila, D.; Weintraub, N.L. Role of oxidative stress in the pathogenesis of abdominal aortic aneurysms. Arterioscler. Thromb. Vasc. Biol. 2007, 27, 461–469. [Google Scholar] [CrossRef] [PubMed]
- Fleming, I.; Mohamed, A.; Galle, J.; Turchanowa, L.; Brandes, R.P.; Fisslthaler, B.; Busse, R. Oxidized low-density lipoprotein increases superoxide production by endothelial nitric oxide synthase by inhibiting PKCalpha. Cardiovasc. Res. 2005, 65, 897–906. [Google Scholar] [CrossRef]
- Honjo, T.; Otsui, K.; Shiraki, R.; Kawashima, S.; Sawamura, T.; Yokoyama, M.; Inoue, N. Essential role of NOXA1 in generation of reactive oxygen species induced by oxidized low-density lipoprotein in human vascular endothelial cells. Endothelium 2008, 15, 137–141. [Google Scholar] [CrossRef]
- Wang, Y.; Che, J.; Zhao, H.; Tang, J.; Shi, G. Osthole alleviates oxidized low-density lipoprotein-induced vascular endothelial injury through suppression of transforming growth factor-β1/Smad pathway. Int. Immunopharmacol. 2018, 65, 373–381. [Google Scholar] [CrossRef]
- Yang, H.; Shi, M.; Richardson, A.; Vijg, J.; Guo, Z. Attenuation of leukocyte-endothelium interaction by antioxidant enzymes. Free Radic. Biol. Med. 2003, 35, 266–276. [Google Scholar] [CrossRef]
- Kim, H.W.; Blomkalns, A.L.; Ogbi, M.; Thomas, M.; Gavrila, D.; Neltner, B.S.; Cassis, L.A.; Thompson, R.W.; Weiss, R.M.; Lindower, P.D.; et al. Role of myeloperoxidase in abdominal aortic aneurysm formation: Mitigation by taurine. Am. J. Physiol. Heart Circ. Physiol. 2017, 1, 1168–1179. [Google Scholar] [CrossRef] [PubMed]
- Emeto, T.I.; Moxon, J.V.; Au, M.; Golledge, J. Oxidative stress and abdominal aortic aneurysm: Potential treatment targets. Clin. Sci. 2016, 130, 301–315. [Google Scholar] [CrossRef] [PubMed]
- Schramm, A.; Matusik, P.; Osmenda, G.; Guzik, T.J. Targeting NADPH oxidases in vascular pharmacology. Vascul. Pharmacol. 2012, 56, 216–231. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, W.; Mactaggart, J.; Knispel, R.; Worth, J.; Zhu, Z.; Yulong, L.; Sun, Y.; Baxter, T.; Johanning, J. Inhibition of reactive oxygen species attenuates aneurysm formation in a murine model. Atherosclerosis 2009, 202, 128–134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fukatsu, H.; Koide, N.; Tada-Oikawa, S.; Izuoka, K.; Ikegami, A.; Ichihara, S.; Ukaji, T.; Morita, N.; Naiki, Y.; Komatsu, T.; et al. NF κB inhibitor DHMEQ inhibits titanium dioxide nanoparticle induced interleukin 1β production: Inhibition of the PM2.5 induced inflammation model. Mol. Med. Rep. 2018, 18, 5279–5285. [Google Scholar] [CrossRef]
- Akerman, A.W.; Stroud, R.E.; Bans, R.W.; Grespin, R.T.; McDonald, L.T.; LaRue, R.A.; Mukherjee, R.; Ikonomidis, J.S.; Jones, J.A.; Ruddy, J.M. Elevated Wall Tension Initiates Interleukin-6 Expression and Abdominal Aortic Dilation. Ann. Vasc. Surg. 2018, 46, 193–204. [Google Scholar] [CrossRef]
- Ray, R.; Shah, A.M. NADPH oxidase and endothelial cell function. Clin. Sci. 2005, 109, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Siu, K.L.; Li, Q.; Zhang, Y.; Guo, J.; Youn, J.Y.; Du, J.; Cai, H. NOX isoforms in the development of abdominal aortic aneurysm. Redox Biol. 2017, 11, 118–125. [Google Scholar] [CrossRef]
- Ramella, M.; Boccafoschi, F.; Bellofatto, K.; Follenzi, A.; Fusaro, L.; Boldorini, R.; Casella, F.; Porta, C.; Settembrini, P.; Cannas, M. Endothelial MMP-9 drives the inflammatory response in abdominal aortic aneurysm (AAA). Am. J. Transl. Res. 2017, 9, 5485. [Google Scholar]
- Madamanchi, N.R.; Runge, M.S. Redox signaling in cardiovascular health and disease. Free Radic. Biol. Med. 2013, 61, 473–501. [Google Scholar] [CrossRef] [Green Version]
- Dawson, J.; Cockerill, G.W.; Choke, E.; Belli, A.M.; Loftus, I.; Thompson, M.M. Aortic aneurysms secrete interleukin-6 into the circulation. J. Vasc. Surg. 2007, 45, 350–356. [Google Scholar] [CrossRef] [Green Version]
- Sprague, A.H.; Khalil, R.A. Inflammatory cytokines in vascular dysfunction and vascular disease. Biochem. Pharmacol. 2009, 78, 539–552. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.K.; Green, L.A.; Gutwein, A.R.; Drucker, N.A.; Motaganahalli, R.L.; Gupta, A.K.; Fajardo, A.; Murphy, M.P. Description of human AAA by cytokine and immune cell aberrations compared to risk-factor matched controls. Surgery 2018, 164, 354–358. [Google Scholar] [CrossRef]
- Choke, E.; Cockerill, G.; Wilson, W.R.; Sayed, S.; Dawson, J.; Loftus, I.; Thompson, M.M. A review of biological factors implicated in abdominal aortic aneurysm rupture. Eur. J. Vasc. Endovasc. Surg. 2005, 30, 227–244. [Google Scholar] [CrossRef]
- Formanowicz, D.; Gutowska, K.; Formanowicz, P. Theoretical Studies on the Engagement of Interleukin 18 in the Immuno-Inflammatory Processes Underlying Atherosclerosis. Int. J. Mol. Sci. 2018, 19, 3476. [Google Scholar] [CrossRef]
- Formanowicz, D.; Radom, M.; Zawierucha, P.; Formanowicz, P. Petri-net-based approach to modeling and analysis of selected aspects of the molecular regulation of angiogenesis. PLoS ONE 2017, 12, e0173020. [Google Scholar] [CrossRef]
- Radom, M.; Rybarczyk, A.; Szawulak, B.; Andrzejewski, H.; Chabelski, P.; Kozak, A.; Formanowicz, P. Holmes: A graphical tool for development, simulation and analysis of Petri-net-based models of complex biological systems. Bioinformatics 2017, 33, 3822–3823. [Google Scholar] [CrossRef]
- Formanowicz, P.; Nowicki, M.; Formanowicz, P. Mathematical modeling of aortic aneurysm progression. In New Approaches to Aortic Diseases from Valve to Abdominal Bifurcation; Tintoiu, I.C., Ursulescu, A., Elefteriades, J.A., Underwood, M.J., Droc, I., Eds.; Academic Press: London, UK, 2018. [Google Scholar]
- Zmijewski, J.W.; Landar, A.; Watanabe, N.; Dickinson, D.A.; Noguchi, N.; Darley-Usmar, V.M. Cell signalling by oxidized lipids and the role of reactive oxygen species in the endothelium. Biochem. Soc. Trans. 2005, 33, 1385–1389. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Schmidt, J.; Ryschich, E.; Mueller-Schilling, M.; Schumacher, H.; Allenberg, J.R. Inducible nitric oxide synthase is present in human abdominal aortic aneurysm and promotes oxidative vascular injury. J. Vasc. Surg. 2003, 38, 360–367. [Google Scholar] [CrossRef]
- Gomez, I.; Ozen, G.; Deschildre, C.; Amgoud, Y.; Boubaya, L.; Gorenne, I.; Benyahia, C.; Roger, T.; Lesèche, G.; Galardon, E.; et al. Reverse Regulatory Pathway (H2S/PGE2/MMP) in Human Aortic Aneurysm and Saphenous Vein Varicosity. PLoS ONE 2016, 11, e0158421. [Google Scholar] [CrossRef]
- Yokoyama, U.; Ishiwata, R.; Jin, M.H.; Kato, Y.; Suzuki, O.; Jin, H.; Ichikawa, Y.; Kumagaya, S.; Katayama, Y.; Fujita, T.; et al. Inhibition of EP4 signaling attenuates aortic aneurysm formation. PLoS ONE 2012, 7, e36724. [Google Scholar] [CrossRef]
- Russell-Puleri, S.; Dela Paz, N.G.; Adams, D.; Chattopadhyay, M.; Cancel, L.; Ebong, E.; Orr, A.W.; Frangos, J.A.; Tarbell, J.M. Fluid shear stress induces upregulation of COX-2 and PGI2 release in endothelial cells via a pathway involving PECAM-1, PI3K, FAK, and p38. Am. J. Physiol. Heart Circ. Physiol. 2017, 312, H485–H500. [Google Scholar] [CrossRef]
- Cao, R.Y.; St Amand, T.; Li, X.; Yoon, S.H.; Wang, C.P.; Song, H.; Maruyama, T.; Brown, P.M.; Zelt, D.T.; Funk, C.D. Prostaglandin receptor EP4 in abdominal aortic aneurysms. Am. J. Pathol. 2012, 181, 313–321. [Google Scholar] [CrossRef]
- Ozen, G.; Gomez, I.; Daci, A.; Deschildre, C.; Boubaya, L.; Teskin, O.; Uydeş-Doğan, B.S.; Jakobsson, P.J.; Longrois, D.; Topal, G.; et al. Inhibition of microsomal PGE synthase-1 reduces human vascular tone by increasing PGI2: A safer alternative to COX-2 inhibition. Br. J. Pharmacol. 2017, 174, 4087–4098. [Google Scholar] [CrossRef]
- Petri, C.A. Communication with Automata; Schriften des Instituts fur Instrumentelle Mathematik: Bonn, Germany, 1962. (In German) [Google Scholar]
- Koch, I.; Reisig, W.; Schreiber, F. (Eds.) Modeling in Systems Biology; The Petri Net Approach; Springer: London, UK, 2011; ISBN 978-1-84996-474-6. [Google Scholar]
- Murata, T. Petri Nets: Properties, Analysis and Applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Reising, W. Understanding Petri Nets. Modeling Techniques, Analysis Methods, Case Studies; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sackmann, A.; Heiner, M.; Koch, I. Application of Petri net-based analysis techniques to signal transduction pathways. BMC Bioinform. 2006, 7, 482. [Google Scholar] [CrossRef]
- Grafahrend-Belau, E.; Schreiber, F.; Heiner, M.; Sackmann, A.; Junker, B.H.; Grunwald, S.; Speer, A.; Winder, K.; Koch, I. Modularization of biochemical networks based on classification of Petri net t-invariants. BMC Bioinform. 2008, 9. [Google Scholar] [CrossRef]
- Formanowicz, D.; Kozak, A.; Głowacki, T.; Radom, M.; Formanowicz, P. Hemojuvelin–Hepcidin axis modeled and analyzed using Petri nets. J. Biomed. Inform. 2013, 46, 1030–1043. [Google Scholar] [CrossRef]
- Formanowicz, D.; Radom, M.; Rybarczyk, A.; Formanowicz, P. The role of Fenton reaction in ROS-induced toxicity underlying atherosclerosis—Modeled and analyzed using a Petri-net-based approach. BioSystems 2018, 165, 71–87. [Google Scholar] [CrossRef]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley and Sons: New York, NY, USA, 1990; ISBN 0-471-87876-6. [Google Scholar]


| Full Model with oxLDL | Reduced Model without oxLDL | ||||
|---|---|---|---|---|---|
| Subprocess | Elementary Subprocess | Frequency Trans/Inv | Percentage of Transition in Whole System (100% = 736 inv) | Frequency Trans/Inv | Percentage of Transition in Whole System (100% = 325 inv) |
| production of O by NOX | 713 | 96.88% | 302 | 92.92% | |
| production of O by NOS and oxLDL | 205 | 27.85% | - | - | |
| oxidative stress | production of O by NOS and BH | 364 | 49.46% | 218 | 67.08% |
| production of ONOO by O and NO | 182 | 24.73% | 109 | 33.54% | |
| production of HO through dismutation | 713 | 96.88% | 302 | 92.92% | |
| production of HOCl by MPO and HO | 707 | 96.06% | 296 | 91.08% | |
| activation by ROS | 197 | 26.77% | 88 | 27.08% | |
| activation by cytokines | 192 | 26.09% | 99 | 30.46% | |
| influence of MMPs | activation of MMP2 by oxLDL | 132 | 17.93% | - | - |
| activation of MPO by HOCl | 184 | 25.00% | 75 | 23.08% | |
| LDL oxidation | LDL oxidation | 411 | 55.84% | - | - |
| activation by oxLDL | 6 | 0.82% | - | - | |
| influence of NOX | activation by TNF | 342 | 46.47% | 143 | 44.00% |
| activation by hemodynamic stress | 145 | 19.70% | 79 | 24.31% | |
| activation by ANGII | 291 | 39.54% | 115 | 35.38% | |
| production by inflammatory cells | 552 | 75.00% | 211 | 64.92% | |
| production by TNF | 108 | 14.67% | 53 | 16.31% | |
| production of inflammatory cytokines | production by NFB | 115 | 15.63% | 55 | 16.92% |
| production by AP1 | 26 | 3.53% | 20 | 6.15% | |
| stimulation of IL-6 | 108 | 14.67% | 53 | 16.31% | |
| enlargement of AAA | enlargement of AAA | 629 | 85.46% | 274 | 84.31% |
| rupture of AAA | rupture of AAA | 260 | 35.33% | 106 | 32.62% |
| Oxidative Stress | Influence of MMPs | LDL Oxidation | Influence of NOX | Production of Inflammatory Cytokines | Enlargement of AAA | Rupture of AAA | |
|---|---|---|---|---|---|---|---|
| full model (with oxLDL) | 98.78% | 80.84% | 55.84% | 96.88% | 93.75% | 85.46% | 35.33% |
| reduced model (without oxLDL) | 97.23% | 78.15% | - | 92.92% | 90.15% | 84.31% | 32.62% |
| knockouted transitions | , , , , , | , , , | , , , | , , , , |
| Full Model with oxLDL | |||||
|---|---|---|---|---|---|
| Significance Analysis of Selected Subprocesses | Knockout of Full Model (Knockout Transition ) | ||||
| Subprocess | Frequency Trans/Inv | Percentage Contribution in Whole System (100% = 736 inv) | Frequency Trans/Inv | Percentage Contribution in Whole System (100% = 325 inv) | Difference between Percentage Contribution (736 inv vs. 325 inv) |
| enlargement of AAA | 629 | 85.46% | 274 | 84.31% | 1.15 p.p. |
| rupture of AAA | 260 | 35.33% | 106 | 32.62% | 2.71 p.p. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutowski, Ł.; Gutowska, K.; Pioruńska-Stolzmann, M.; Formanowicz, P.; Formanowicz, D. Systems Approach to Study Associations between OxLDL and Abdominal Aortic Aneurysms. Int. J. Mol. Sci. 2019, 20, 3909. https://doi.org/10.3390/ijms20163909
Gutowski Ł, Gutowska K, Pioruńska-Stolzmann M, Formanowicz P, Formanowicz D. Systems Approach to Study Associations between OxLDL and Abdominal Aortic Aneurysms. International Journal of Molecular Sciences. 2019; 20(16):3909. https://doi.org/10.3390/ijms20163909
Chicago/Turabian StyleGutowski, Łukasz, Kaja Gutowska, Maria Pioruńska-Stolzmann, Piotr Formanowicz, and Dorota Formanowicz. 2019. "Systems Approach to Study Associations between OxLDL and Abdominal Aortic Aneurysms" International Journal of Molecular Sciences 20, no. 16: 3909. https://doi.org/10.3390/ijms20163909
APA StyleGutowski, Ł., Gutowska, K., Pioruńska-Stolzmann, M., Formanowicz, P., & Formanowicz, D. (2019). Systems Approach to Study Associations between OxLDL and Abdominal Aortic Aneurysms. International Journal of Molecular Sciences, 20(16), 3909. https://doi.org/10.3390/ijms20163909