Application of the Movable Type Free Energy Method to the Caspase-Inhibitor Binding Affinity Study
Abstract
:1. Introduction
2. Results and Discussion
2.1. Large-Scale Validation Benchmark
2.2. Test Benchmark Studying the Binding ∆∆G Regarding the Structural Changes at the Binding Interface
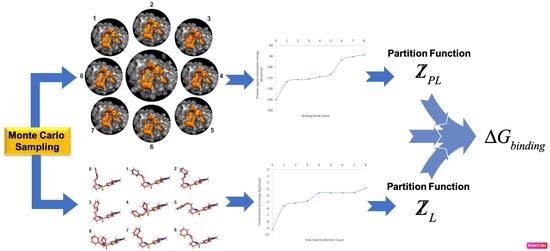
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Alzheimer’s Disease |
| MT | Movable Type |
| NFTs | Neurofibrillary tangles |
References
- Rohn, T.T.; Head, E.; Su, J.H.; Anderson, A.J.; Bahr, B.A.; Cotman, C.W.; Cribbs, D.H. Correlation between caspase activation and neurofibrillary tangle formation in Alzheimer’s disease. Am. J. Pathol. 2001, 158, 189–198. [Google Scholar] [CrossRef]
- Stadelmann, C.; Deckwerth, T.L.; Srinivasan, A.; Bancher, C.; Brück, W.; Jellinger, K.; Lassmann, H. Activation of caspase-3 in single neurons and autophagic granules of granulovacuolar degeneration in Alzheimer’s disease. Evidence for apoptotic cell death. Am. J. Pathol. 1999, 155, 1459–1466. [Google Scholar] [CrossRef]
- Gervais, F.G.; Xu, D.; Robertson, G.S.; Vaillancourt, J.P.; Zhu, Y.; Huang, J.; LeBlanc, A.; Smith, D.; Rigby, M.; Shearman, M.S.; et al. Involvement of caspases in proteolytic cleavage of Alzheimer’s amyloid-beta precursor protein and amyloidogenic A beta peptide formation. Cell 1999, 97, 395–406. [Google Scholar] [CrossRef]
- Cotman, C.W.; Poon, W.W.; Rissman, R.A.; Blurton-Jones, M. The role of caspase cleavage of tau in Alzheimer disease neuropathology. J. Neuropathol. Exp. Neurol. 2005, 64, 104–112. [Google Scholar] [CrossRef] [PubMed]
- Roth, K.A. Caspases, apoptosis, and Alzheimer disease: Causation, correlation, and confusion. J. Neuropathol. Exp. Neurol. 2001, 60, 829–838. [Google Scholar] [CrossRef] [PubMed]
- Obulesu, M.; Lakshmi, M.J. Apoptosis in Alzheimer’s disease: An understanding of the physiology, pathology and therapeutic avenues. Neurochem. Res. 2014, 39, 2301–2312. [Google Scholar] [CrossRef] [PubMed]
- Cribbs, D.H.; Poon, W.W.; Rissman, R.A.; Blurton-Jones, M. Caspase-Mediated Degeneration in Alzheimer’s Disease. Am. J. Pathol. 2004, 165, 353–355. [Google Scholar] [CrossRef]
- Kim, T.W.; Pettingell, W.H.; Jung, Y.K.; Kovacs, D.M.; Tanzi, R.E. Alternative cleavage of Alzheimer-associated presenilins during apoptosis by a caspase-3 family protease. Science 1997, 277, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Gamblin, T.C.; Chen, F.; Zambrano, A.; Abraha, A.; Lagalwar, S.; Guillozet, A.L.; Lu, M.; Fu, Y.; Garcia-Sierra, F.; LaPointe, N.; et al. Caspase cleavage of tau: Linking amyloid and neurofibrillary tangles in Alzheimer’s disease. Proc. Natl. Acad. Sci. USA 2003, 100, 10032–10037. [Google Scholar] [CrossRef] [PubMed]
- Rissman, R.A.; Poon, W.W.; Blurton-Jones, M.; Oddo, S.; Torp, R.; Vitek, M.P.; LaFerla, F.M.; Rohn, T.T.; Cotman, C.W. Caspase-cleavage of tau is an early event in Alzheimer disease tangle pathology. J. Clin. Investig. 2004, 114, 121–130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Binder, L.I.; Guillozet-Bongaarts, A.L.; Garcia-Sierra, F.; Berry, R.W. Tau, tangles, and Alzheimer’s disease. Biochim. Biophys. Acta Mol. Basis Dis. 2005, 1739, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Leroy, K.; Ando, K.; Laporte, V.; Dedecker, R.; Suain, V.; Authelet, M.; Héraud, C.; Pierrot, N.; Yilmaz, Z.; Octave, J.N.; et al. Lack of tau proteins rescues neuronal cell death and decreases amyloidogenic processing of APP in APP/PS1 mice. Am. J. Pathol. 2012, 181, 1928–1940. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Albrecht, S.; Bourdeau, M.; Petzke, T.; Bergeron, C.; LeBlanc, A.C. Active caspase-6 and caspase-6-cleaved tau in neuropil threads, neuritic plaques, and neurofibrillary tangles of Alzheimer’s disease. Am. J. Pathol. 2004, 165, 523–531. [Google Scholar] [CrossRef]
- Rohn, T.T.; Rissman, R.A.; Davis, M.C.; Kim, Y.E.; Cotman, C.W.; Head, E. Caspase-9 activation and caspase cleavage of tau in the Alzheimer’s disease brain. Neurobiol. Dis. 2002, 11, 341–354. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, A.; Liu, H.; Goodyer, C.; Bergeron, C.; Hammond, J. Caspase-6 role in apoptosis of human neurons, amyloidogenesis, and Alzheimer’s disease. J. Biol. Chem. 1999, 274, 23426–23436. [Google Scholar] [CrossRef] [PubMed]
- Klaiman, G.; Petzke, T.L.; Hammond, J.; Leblanc, A.C. Targets of caspase-6 activity in human neurons and Alzheimer disease. Mol. Cell Proteom. 2008, 7, 1541–1555. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, P.M.; Patterson, K.R.; Guillozet-Bongaarts, A.L.; Reynolds, M.R.; Carroll, C.A.; Weintraub, S.T.; Bennett, D.A.; Cryns, V.L.; Berry, R.W.; Binder, L.I. Early N-terminal changes and caspase-6 cleavage of tau in Alzheimer’s disease. J. Neurosci. 2004, 24, 7895–7902. [Google Scholar] [CrossRef]
- Su, J.H.; Zhao, M.; Anderson, A.J.; Srinivasan, A.; Cotman, C.W. Activated caspase-3 expression in Alzheimer’s and aged control brain: Correlation with Alzheimer pathology. Brain Res. 2001, 898, 350–357. [Google Scholar] [CrossRef]
- Rohn, T.T.; Head, E.; Nesse, W.H.; Cotman, C.W.; Cribbs, D.H. Activation of caspase-8 in the Alzheimer’s disease brain. Neurobiol. Dis. 2001, 8, 1006–1016. [Google Scholar] [CrossRef]
- Pate, K.M.; Rogers, M.; Reed, J.W.; van der Munnik, N.; Vance, S.Z.; Moss, M.A. Anthoxanthin Polyphenols Attenuate Aβ Oligomer-induced Neuronal Responses Associated with Alzheimer’s Disease. CNS Neurosci. Ther. 2017, 23, 135–144. [Google Scholar] [CrossRef]
- Pérez, M.J.; Vergara-Pulgar, K.; Jara, C.; Cabezas-Opazo, F.; Quintanilla, R.A. Caspase-Cleaved Tau Impairs Mitochondrial Dynamics in Alzheimer’s Disease. Mol. Neurobiol. 2018, 55, 1004–1018. [Google Scholar] [CrossRef] [PubMed]
- Forner, S.; Baglietto-Vargas, D.; Martini, A.C.; Trujillo-Estrada, L.; LaFerla, F.M. Synaptic Impairment in Alzheimer’s Disease: A Dysregulated Symphony. Trends Neurosci. 2017, 40, 347–357. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.; Lauretti, E.; Praticò, D. Caspase-3-dependent cleavage of Akt modulates tau phosphorylation via GSK3β kinase: Implications for Alzheimer’s disease. Mol. Psychiatry. 2017, 22, 1002–1008. [Google Scholar] [CrossRef] [PubMed]
- Rohn, T.T. The role of caspases in Alzheimer’s disease; potential novel therapeutic opportunities. Apoptosis 2010, 15, 1403–1409. [Google Scholar] [CrossRef] [PubMed]
- Gilson, M.K.; Zhou, H.X. Calculation of protein-ligand binding affinities. Annu. Rev. Bioph. Biom. 2007, 36, 21–42. [Google Scholar] [CrossRef] [PubMed]
- Michel, J.; Essex, J.W. Prediction of protein-ligand binding affinity by free energy simulations: Assumptions, pitfalls and expectations. J. Comput. Aid. Mol Des. 2010, 24, 639–658. [Google Scholar] [CrossRef]
- Shirts, M.R.; Mobley, D.L.; Chodera, J.D. Alchemical Free Energy Calculations: Ready for Prime Time? Ann. Rep. Comp. Chem. 2007, 3, 41–59. [Google Scholar]
- Halperin, I.; Ma, B.Y.; Wolfson, H.; Nussinov, R. Principles of docking: An overview of search algorithms and a guide to scoring functions. Proteins 2002, 47, 409–443. [Google Scholar] [CrossRef]
- Yuriev, E.; Ramsland, P.A. Latest developments in molecular docking: 2010-2011 in review. J. Mol. Recognit. 2013, 26, 215–239. [Google Scholar] [CrossRef]
- Kollman, P.A.; Massova, I.; Reyes, C.; Kuhn, B.; Huo, S.; Chong, L.; Lee, M.; Lee, T.; Duan, Y.; Wang, W.; et al. Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33, 889–897. [Google Scholar] [CrossRef]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Mobley, D.L.; Shirts, M.R.; Dixon, R.W.; Branson, K.; Pande, V.S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struc. Biol. 2011, 21, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Christ, C.D.; Mark, A.E.; van Gunsteren, W.F. Feature Article Basic Ingredients of Free Energy Calculations: A Review. J. Comput. Chem. 2010, 31, 1569–1582. [Google Scholar] [PubMed]
- Woo, H.J.; Roux, B. Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. USA 2005, 102, 6825–6830. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R.W. High-Temperature Equation of State by a Perturbation Method.1. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Buch, I.; Sadiq, S.K.; De Fabritiis, G. Optimized Potential of Mean Force Calculations for Standard Binding Free Energies. J. Chem. Theory Comput. 2011, 7, 1765–1772. [Google Scholar] [CrossRef] [PubMed]
- Essex, J.W.; Severance, D.L.; TiradoRives, J.; Jorgensen, W.L. Monte Carlo simulations for proteins: Binding affinities for trypsin-benzamidine complexes via free-energy perturbations. J. Phys. Chem. B 1997, 101, 9663–9669. [Google Scholar] [CrossRef]
- Gumbart, J.C.; Roux, B.; Chipot, C. Standard Binding Free Energies from Computer Simulations: What Is the Best Strategy? J. Chem. Theory Comput. 2013, 9, 794–802. [Google Scholar] [CrossRef]
- Roux, B. The Calculation of the Potential of Mean Force Using Computer-Simulations. Comput. Phys. Commun. 1995, 91, 275–282. [Google Scholar] [CrossRef]
- Jorgensen, W.L. Free-Energy Calculations—a Breakthrough for Modeling Organic-Chemistry in Solution. Accounts Chem. Res. 1989, 22, 184–189. [Google Scholar] [CrossRef]
- Klimovich, P.V.; Shirts, M.R.; Mobley, D.L. Guidelines for the analysis of free energy calculations. J. Comput. Aid. Mol Des. 2015, 29, 397–411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shirts, M.R.; Mobley, D.L. An introduction to best practices in free energy calculations. Methods Mol. Biol. 2013, 924, 271–311. [Google Scholar] [PubMed]
- Zheng, Z.; Ucisik, M.N.; Merz, K.M., Jr. The Movable Type Method Applied to Protein–Ligand Binding. J. Chem. Theory Comput. 2013, 9, 5526–5538. [Google Scholar] [CrossRef]
- Liu, T.; Lin, Y.; Wen, X.; Jorissen, R.N.; Gilson, M.K. BindingDB: A web-accessible database of experimentally determined protein-ligand binding affinities. Nucleic Acids Res. 2007, 35, D198–D201. [Google Scholar] [CrossRef] [PubMed]
- Gilson, M.K.; Liu, T.; Baitaluk, M.; Nicola, G.; Hwang, L.; Chong, J. BindingDB in 2015: A public database for medicinal chemistry, computational chemistry and systems pharmacology. Nucleic Acids Res. 2016, 44, D1045–D1053. [Google Scholar] [CrossRef] [PubMed]
- Mysinger, M.M.; Carchia, M.; Irwin, J.J.; Shoichet, B.K. Directory of Useful Decoys, Enhanced (DUD-E): Better Ligands and Decoys for Better Benchmarking. J. Med. Chem. 2012, 55, 6582–6594. [Google Scholar] [CrossRef]
- Gaulton, A.; Bellis, L.J.; Bento, A.P.; Chambers, J.; Davies, M.; Hersey, A.; Light, Y.; McGlinchey, S.; Michalovich, D.; Al-Lazikani, B.; et al. ChEMBL: A large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2012, 40, D1100–D1107. [Google Scholar] [CrossRef]
- Cheng, Y.; Prusoff, W.H. Relationship between the inhibition constant (KI) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem. Pharm. 1973, 22, 3099–3108. [Google Scholar]
- Kalliokoski, T.; Kramer, C.; Vulpetti, A.; Gedeck, P. Comparability of mixed IC50 data—a statistical analysis. PLoS ONE 2013, 8, e61007. [Google Scholar] [CrossRef]
- Kastritis, P.L.; Rodrigues, J.P.G.L.M.; Bonvin, A.M.J.J. HADDOCK2P2I: A Biophysical Model for Predicting the Binding Affinity of Protein–Protein Interaction Inhibitors. J. Chem. Inf. Model. 2014, 54, 826–836. [Google Scholar] [CrossRef] [PubMed]
- Sakkiah, S.; Thangapandian, S.; John, S.; Kwon, Y.J.; Lee, K.W. 3D QSAR pharmacophore based virtual screening and molecular docking for identification of potential HSP90 inhibitors. Eur. J. Med. Chem. 2010, 45, 2132–2140. [Google Scholar] [CrossRef] [PubMed]
- Schneider, G.; Odile, C.; Hilfiger, L.; Schneider, P.; Kirsch, S.; Böhm, H.; Neidhart, W. Virtual Screening for Bioactive Molecules by Evolutionary De Novo Design. Angew. Chem. Int. Ed. 2000, 39, 4130–4133. [Google Scholar] [CrossRef]
- Bansal, N.; Zheng, Z.; Song, L.F.; Pei, J.; Merz, K.M., Jr. The Role of the Active Site Flap in Streptavidin/Biotin Complex Formation. J. Am. Chem. Soc. 2018, 140, 5434–5446. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Zheng, Z.; Wang, T.; Merz, K.M., Jr. A Free Energy Based Conformational Search Algorithm Using the “Movable Type” Sampling Method. J. Chem. Theory Comput. 2015, 11, 5853–5864. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Pei, J.; Bansal, N.; Liu, H.; Song, L.F.; Merz, K.M., Jr. Generation of Pairwise Potentials Using Multi-Dimensional Data Mining. J. Chem. Theory Comput. 2018, 14, 5045–5067. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Wang, T.; Li, P.; Merz, K.M., Jr. KECSA-Movable Type Implicit Solvation Model (KMTISM). J. Chem. Theory Comput. 2014, 11, 667–682. [Google Scholar] [CrossRef] [Green Version]











| PDB ID | Ligand | Ligand Mass (Da) | Experimental ΔG (kcal/mol) | Calculated ΔG (kcal/mol) |
|---|---|---|---|---|
| 3h0e |  | 455.57 | −11.11 | −9.15 |
| 1gfw |  | 400.45 | −10.66 | −10.34 |
| 3dei |  | 366.32 | −10.08 | −8.56 |
| 3dej |  | 400.77 | −10.90 | −8.46 |
| 3dek |  | 427.38 | −10.32 | −10.37 |
| 1nms |  | 464.45 | −9.13 | −9.46 |
| 1re1 |  | 301.09 | −7.099 | −7.133 |
| 1rhm |  | 301.09 | −7.849 | −7.728 |
| PDB ID | Ligand | Ligand Mass (Da) | Experimental ΔG (kcal/mol) | Calculated ΔG (kcal/mol) |
|---|---|---|---|---|
| 1rhu | 5,6,7 tricyclic peptidomimetic | 638.69 | −11.61 | −10.88 |
| 1rhr | Cinnamic acid methyl ester | 651.14 | −11.04 | −10.79 |
| 1rhj | Pryazinone | 574.69 | −10.96 | −11.02 |
| 4jje | ACE-1MH-ASP-B3L-HLX-1U8 (Unnatural amino acid peptides) | 838.94 | −10.41 | −10.90 |
| 2h5i | Ac-DEVD-Cho | 504.49 | −12.11 | −11.18 |
| 2h5j | Ac-DMQD-Cho | 535.57 | −10.779 | −11.06 |
| 4jr0 | Ac-DEVD-CMK | 552.96 | −11.17 | −11.26 |
| 3gjt | Ac-IEPD (Diverse P4 Residues in Peptides) | 498.13 | −9.23 | −9.44 |
| PDB ID | Caspase Target | Peptide Ligand | Experimental ΔG (kcal/mol) | Calculated ΔG (kcal/mol) |
|---|---|---|---|---|
| 2h5j | caspase-3 | Ac-DMQD-Cho | −10.78 | −11.06 |
| 2ql5 | caspase-7 | Ac-DMQD-Cho | −11.04 | −12.72 |
| 2ql9 | caspase-7 | Ac-DQMD-Cho | −12.30 | −12.51 |
| 2qlf | caspase-7 | Ac-DNLD-Cho | −12.06 | −12.26 |
| 2qlb | caspase-7 | Ac-EMSD-Cho | −8.03 | −8.46 |
| 2ql7 | caspase-7 | Ac-IEPD-Cho | −8.53 | −8.16 |
| 1f1j | caspase-7 | Ac-DEVD-Cho | −11.99 | −10.74 |
| 2h5i | caspase-3 | Ac-DEVD-Cho | −12.11 | −11.18 |
| 4jr0 | caspase-3 | Ac-DEVD-CMK | −11.17 | −11.26 |
| 3r7b | caspase-2 | Ac-DVAD-Cho | −8.38 | −8.42 |
| 3r5j | caspase-2 | Ac-ADVAD-Cho | −9.48 | −9.72 |
| 3r6g | caspase-2 | Ac-VDVAD-Cho | −10.36 | −10.68 |
| 3gjt | caspase-3 | Ac-IEPD | −9.23 | −9.44 |
| 1f9e | caspase-8 | Phq-DEVD | −11.86 | −10.49 |
| 4jje | caspase-3 | Ac-1MH-ASP-B3L-HLX-1U8 | −10.41 | −10.90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, S.; Liu, H.; Zheng, Z. Application of the Movable Type Free Energy Method to the Caspase-Inhibitor Binding Affinity Study. Int. J. Mol. Sci. 2019, 20, 4850. https://doi.org/10.3390/ijms20194850
Xue S, Liu H, Zheng Z. Application of the Movable Type Free Energy Method to the Caspase-Inhibitor Binding Affinity Study. International Journal of Molecular Sciences. 2019; 20(19):4850. https://doi.org/10.3390/ijms20194850
Chicago/Turabian StyleXue, Song, Hao Liu, and Zheng Zheng. 2019. "Application of the Movable Type Free Energy Method to the Caspase-Inhibitor Binding Affinity Study" International Journal of Molecular Sciences 20, no. 19: 4850. https://doi.org/10.3390/ijms20194850
APA StyleXue, S., Liu, H., & Zheng, Z. (2019). Application of the Movable Type Free Energy Method to the Caspase-Inhibitor Binding Affinity Study. International Journal of Molecular Sciences, 20(19), 4850. https://doi.org/10.3390/ijms20194850