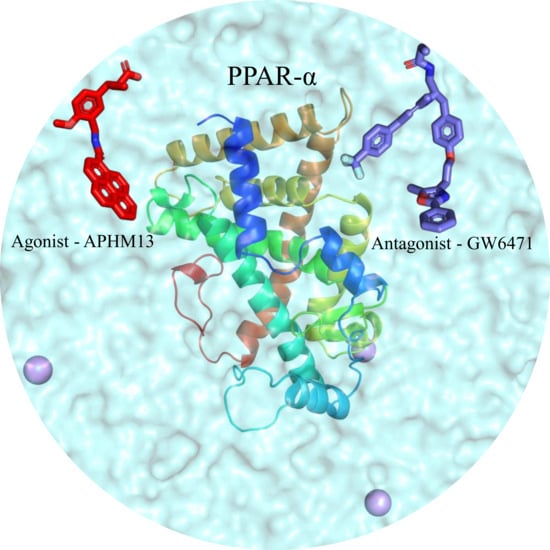
A Molecular Dynamics Approach to Explore the Intramolecular Signal Transduction of PPAR-α
Abstract
:1. Introduction
2. Results and Discussion
2.1. Structural Stability of PPAR-α Complexes During Simulations
2.2. Hydrogen Bond Analysis
2.3. Essential Dynamics Analysis
2.4. Generation of PPAR-α Minimal Energy Structures
2.5. Network Centrality Analysis
3. Materials and Methods
3.1. Computing and Data Analysis
3.2. Preparation of the Apo, Agonist-, and Antagonist-Bound Structures
3.3. Molecular Dynamics (MD) Simulations
3.4. Principal Component Analysis (PCA) and Free Energy Landscape (FEL)
3.5. Residue Interaction Network Construction
3.6. Network Centralities
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PPAR-α | Peroxisome proliferator-activated receptor-α |
| MD | Molecular dynamics |
| LBD | Ligand binding domain |
| RMSD | Root mean square deviation |
| RMSF | Root mean square fluctuation |
| PCA | Principal component analysis |
| FEL | Free energy landscape |
| 2D | Two-dimensional |
| CB | Betweenness centrality |
| CC | Closeness centrality |
| CD | Degree centrality |
References
- Daynes, R.A.; Jones, D.C. Emerging roles of PPARs in inflammation and immunity. Nat. Rev. Immunol. 2002, 2, 748–759. [Google Scholar] [CrossRef]
- Desvergne, B.; Wahli, W. Peroxisome proliferator-activated receptors: nuclear control of metabolism. Endocr. Rev. 1999, 20, 649–688. [Google Scholar] [CrossRef]
- Clark, R.B. The role of PPARs in inflammation and immunity. J. Leukoc. Biol. 2002, 71, 388–400. [Google Scholar]
- Varga, T.; Czimmerer, Z.; Nagy, L. PPARs are a unique set of fatty acid regulated transcription factors controlling both lipid metabolism and inflammation. Biochim. Biophys. Acta 2011, 1812, 1007–1022. [Google Scholar] [CrossRef] [PubMed]
- Levine, B.; Mizushima, N.; Virgin, H.W. Autophagy in immunity and inflammation. Nature 2011, 469, 323–335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grygiel-Gorniak, B. Peroxisome proliferator-activated receptors and their ligands: nutritional and clinical implications—A review. Nutr. J. 2014, 13, 17. [Google Scholar] [CrossRef]
- Contreras, A.V.; Torres, N.; Tovar, A.R. PPAR-alpha as a key nutritional and environmental sensor for metabolic adaptation. Adv. Nutr. 2013, 4, 439–452. [Google Scholar] [CrossRef] [PubMed]
- Issemann, I.; Green, S. Activation of a member of the steroid hormone receptor superfamily by peroxisome proliferators. Nature 1990, 347, 645–650. [Google Scholar] [CrossRef]
- Lefebvre, P.; Chinetti, G.; Fruchart, J.C.; Staels, B. Sorting out the roles of PPAR alpha in energy metabolism and vascular homeostasis. J. Clin. Investig. 2006, 116, 571–580. [Google Scholar] [CrossRef] [PubMed]
- Moran, E.P.; Ma, J.X. Therapeutic Effects of PPAR alpha on Neuronal Death and Microvascular Impairment. PPAR Res. 2015, 2015, 595426. [Google Scholar] [CrossRef] [PubMed]
- Kersten, S. Integrated physiology and systems biology of PPARalpha. Mol. Metab. 2014, 3, 354–371. [Google Scholar] [CrossRef] [PubMed]
- Schoonjans, K.; Staels, B.; Auwerx, J. The peroxisome proliferator activated receptors (PPARS) and their effects on lipid metabolism and adipocyte differentiation. Biochim. Biophys. Acta 1996, 1302, 93–109. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, H.M.; Kim, J.K.; Yang, C.S.; Kim, T.S.; Jung, M.; Jin, H.S.; Kim, S.; Jang, J.; Oh, G.T.; et al. PPAR-alpha Activation Mediates Innate Host Defense through Induction of TFEB and Lipid Catabolism. J. Immunol. 2017, 198, 3283–3295. [Google Scholar] [CrossRef] [PubMed]
- Kuwabara, N.; Oyama, T.; Tomioka, D.; Ohashi, M.; Yanagisawa, J.; Shimizu, T.; Miyachi, H. Peroxisome proliferator-activated receptors (PPARs) have multiple binding points that accommodate ligands in various conformations: phenylpropanoic acid-type PPAR ligands bind to PPAR in different conformations, depending on the subtype. J. Med. Chem. 2012, 55, 893–902. [Google Scholar] [CrossRef]
- Xu, H.E.; Stanley, T.B.; Montana, V.G.; Lambert, M.H.; Shearer, B.G.; Cobb, J.E.; McKee, D.D.; Galardi, C.M.; Plunket, K.D.; Nolte, R.T.; et al. Structural basis for antagonist-mediated recruitment of nuclear co-repressors by PPARalpha. Nature 2002, 415, 813–817. [Google Scholar] [CrossRef]
- Lee, Y.; Basith, S.; Choi, S. Recent Advances in Structure-Based Drug Design Targeting Class A G Protein-Coupled Receptors Utilizing Crystal Structures and Computational Simulations. J. Med. Chem. 2018, 61, 1–46. [Google Scholar] [CrossRef]
- Liu, M.; Wang, L.; Zhao, X.; Sun, X. Molecular recognition of agonist and antagonist for peroxisome proliferator-activated receptor-alpha studied by molecular dynamics simulations. Int. J. Mol. Sci. 2014, 15, 8743–8752. [Google Scholar] [CrossRef]
- Chan, M.K.; Mukund, S.; Kletzin, A.; Adams, M.W.; Rees, D.C. Structure of a hyperthermophilic tungstopterin enzyme, aldehyde ferredoxin oxidoreductase. Science 1995, 267, 1463–1469. [Google Scholar] [CrossRef]
- Salentin, S.; Haupt, V.J.; Daminelli, S.; Schroeder, M. Polypharmacology rescored: protein-ligand interaction profiles for remote binding site similarity assessment. Prog. Biophys. Mol. Biol. 2014, 116, 174–186. [Google Scholar] [CrossRef]
- Van der Spoel, D.; van Maaren, P.J.; Larsson, P.; Timneanu, N. Thermodynamics of hydrogen bonding in hydrophilic and hydrophobic media. J. Phys. Chem. B 2006, 110, 4393–4398. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.; Mason, S.P.; Barabasi, A.L.; Oltvai, Z.N. Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef] [Green Version]
- Basith, S.; Lee, Y.; Choi, S. Understanding G protein-coupled receptor allostery via molecular dynamics simulations: Implications for drug discovery. In Computational Drug Discovery and Design; Springer: Berlin/Heidelberg, Germany, 2018; pp. 455–472. [Google Scholar]
- Whitley, M.J.; Lee, A.L. Frameworks for understanding long-range intra-protein communication. Curr. Protein Pept. Sci. 2009, 10, 116–127. [Google Scholar] [CrossRef] [PubMed]
- De Ruvo, M.; Giuliani, A.; Paci, P.; Santoni, D.; Di Paola, L. Shedding light on protein-ligand binding by graph theory: the topological nature of allostery. Biophys. Chem. 2012, 165–166, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Amitai, G.; Shemesh, A.; Sitbon, E.; Shklar, M.; Netanely, D.; Venger, I.; Pietrokovski, S. Network analysis of protein structures identifies functional residues. J. Mol. Biol. 2004, 344, 1135–1146. [Google Scholar] [CrossRef]
- Gosu, V.; Son, S.; Shin, D.; Song, K.-D. Insights into the dynamic nature of the dsRNA-bound TLR3 complex. Sci. Rep. 2019, 9, 3652. [Google Scholar] [CrossRef]
- Lee, Y.; Choi, S.; Hyeon, C. Mapping the intramolecular signal transduction of G-protein coupled receptors. Proteins 2014, 82, 727–743. [Google Scholar] [CrossRef]
- Berendsen, H.J.; van der Spoel, D.; van Drunen, R. GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Schrodinger, LLC. The PyMOL Molecular Graphics System, Version 2.3.0a0; Schrodinger, LLC: New York, NY, USA, 2015. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90. [Google Scholar] [CrossRef]
- Pieper, U.; Webb, B.M.; Dong, G.Q.; Schneidman-Duhovny, D.; Fan, H.; Kim, S.J.; Khuri, N.; Spill, Y.G.; Weinkam, P.; Hammel, M.; et al. ModBase, a database of annotated comparative protein structure models and associated resources. Nucleic Acids Res. 2014, 42, D336–D346. [Google Scholar] [CrossRef] [PubMed]
- Sierra, M.L.; Beneton, V.; Boullay, A.B.; Boyer, T.; Brewster, A.G.; Donche, F.; Forest, M.C.; Fouchet, M.H.; Gellibert, F.J.; Grillot, D.A.; et al. Substituted 2-[(4-aminomethyl)phenoxy]-2-methylpropionic acid PPARalpha agonists. 1. Discovery of a novel series of potent HDLc raising agents. J. Med. Chem. 2007, 50, 685–695. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminform. 2011, 3, 33. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- David, C.C.; Jacobs, D.J. Principal component analysis: a method for determining the essential dynamics of proteins. Methods Mol. Biol. 2014, 1084, 193–226. [Google Scholar] [CrossRef] [PubMed]
- Amadei, A.; Linssen, A.B.; Berendsen, H.J. Essential dynamics of proteins. Proteins 1993, 17, 412–425. [Google Scholar] [CrossRef] [PubMed]
- Basith, S.; Manavalan, B.; Gosu, V.; Choi, S. Evolutionary, structural and functional interplay of the IkappaB family members. PLoS ONE 2013, 8, e54178. [Google Scholar] [CrossRef]
- Yamaguchi, H.; van Aalten, D.M.; Pinak, M.; Furukawa, A.; Osman, R. Essential dynamics of DNA containing a cis.syn cyclobutane thymine dimer lesion. Nucleic Acids Res. 1998, 26, 1939–1946. [Google Scholar] [CrossRef] [Green Version]
- Van Aalten, D.M.; Findlay, J.B.; Amadei, A.; Berendsen, H.J. Essential dynamics of the cellular retinol-binding protein—Evidence for ligand-induced conformational changes. Protein Eng. 1995, 8, 1129–1135. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Saranathan, R.; Prashanth, K.; Tiwary, B.K.; Krishna, R. Inhibition of the MurA enzyme in Fusobacterium nucleatum by potential inhibitors identified through computational and in vitro approaches. Mol. Biosyst. 2017, 13, 939–954. [Google Scholar] [CrossRef]
- Bharathi, A.C.; Yadav, P.K.; Syed Ibrahim, B. Sequence diversity and ligand-induced structural rearrangements of viper hyaluronidase. Mol. Biosyst. 2016, 12, 1128–1138. [Google Scholar] [CrossRef] [PubMed]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]








| CBApo ≥ 0.05 | CBAgo ≥ 0.05 | CBAntag ≥ 0.05 |
|---|---|---|
| Y311, L321 | F290, Y314, F361, Y464 | S280, F318, I354, M355 |
| |CBApo − CBAgo| ≥ 0.02 | |CBApo − CBAntag| ≥ 0.02 |
|---|---|
| L229, I272, F273, Q277, Y311, L321, V324, M325, M330, I382, Q401, E462, Y464 | L229, Q277, S280, L309, Y311, V313, F318, L321, M325, I354, M355, F378, K448, E451, E462 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basith, S.; Manavalan, B.; Shin, T.H.; Lee, G. A Molecular Dynamics Approach to Explore the Intramolecular Signal Transduction of PPAR-α. Int. J. Mol. Sci. 2019, 20, 1666. https://doi.org/10.3390/ijms20071666
Basith S, Manavalan B, Shin TH, Lee G. A Molecular Dynamics Approach to Explore the Intramolecular Signal Transduction of PPAR-α. International Journal of Molecular Sciences. 2019; 20(7):1666. https://doi.org/10.3390/ijms20071666
Chicago/Turabian StyleBasith, Shaherin, Balachandran Manavalan, Tae Hwan Shin, and Gwang Lee. 2019. "A Molecular Dynamics Approach to Explore the Intramolecular Signal Transduction of PPAR-α" International Journal of Molecular Sciences 20, no. 7: 1666. https://doi.org/10.3390/ijms20071666
APA StyleBasith, S., Manavalan, B., Shin, T. H., & Lee, G. (2019). A Molecular Dynamics Approach to Explore the Intramolecular Signal Transduction of PPAR-α. International Journal of Molecular Sciences, 20(7), 1666. https://doi.org/10.3390/ijms20071666