Rescoring and Linearly Combining: A Highly Effective Consensus Strategy for Virtual Screening Campaigns
Abstract
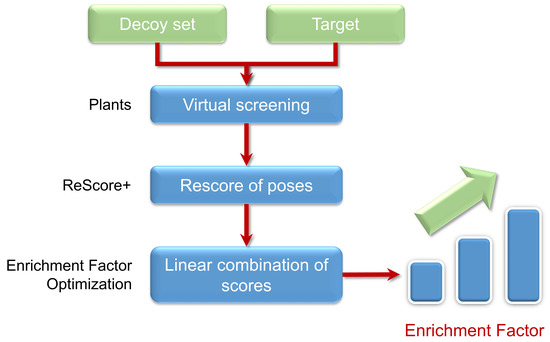
:1. Introduction
2. Results and Discussion
2.1. Single Variable Models
2.2. Two-Variable Consensus Models
2.3. Three-Variable Consensus Models
2.4. Comparison with Already Published Studies
3. Materials and Methods
3.1. Preparation of DUD Datasets
3.2. Docking Simulations
3.3. Generation and Validation of Predictive Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACO | Ant Colony Optimization |
| AUC | Area Under the Curve |
| DUD | Directory of Useful Decoys |
| EF | Enrichment Factor |
| EFO | Enrichment Factor Optimization |
| HTS | High Throughput Screening |
| MLP | Molecular Lipophilicity Potential |
| VIF | Variance Inflation Factor |
| VS | Virtual Screening |
References
- Wingert, B.M.; Camacho, C.J. Improving small molecule virtual screening strategies for the next generation of therapeutics. Curr. Opin. Chem. Biol. 2018, 44, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Truchon, J.F.; Bayly, C.I. Evaluating virtual screening methods: Good and bad metrics for the "early recognition" problem. J. Chem. Inf. Model 2007, 47, 488–508. [Google Scholar] [CrossRef] [PubMed]
- Lagarde, N.; Zagury, J.F.; Montes, M. Benchmarking Data Sets for the Evaluation of Virtual Ligand Screening Methods: Review and Perspectives. J. Chem. Inf. Model 2015, 55, 1297–1307. [Google Scholar] [CrossRef] [PubMed]
- Halder, A.K.; Saha, A.; Jha, T. The role of 3D pharmacophore mapping based virtual screening for identification of novel anticancer agents: An overview. Curr. Top. Med. Chem. 2013, 13, 1098–1126. [Google Scholar] [CrossRef] [PubMed]
- Chemi, G.; Gemma, S.; Campiani, G.; Brogi, S.; Butini, S.; Brindisi, M. Computational Tool for Fast in silico Evaluation of hERG K+ Channel Affinity. Front. Chem. 2017, 5. eCollection 2017. [Google Scholar] [CrossRef]
- Hoffer, L.; Muller, C.; Roche, P.; Morelli, X. Chemistry-driven Hit-to-lead Optimization Guided by Structure-based Approaches. Mol. Inform. 2018, 37, e1800059. [Google Scholar] [CrossRef] [PubMed]
- Zaccagnini, L.; Brogi, S.; Brindisi, M.; Gemma, S.; Chemi, G.; Legname, G.; Campiani, G.; Butini, S. Identification of novel fluorescent probes preventing PrPSc replication in prion diseases. Eur. J. Med. Chem. 2017, 127, 859–873. [Google Scholar] [CrossRef]
- Myrianthopoulos, V.; Lambrinidis, G.; Mikros, E. In Silico Screening of Compound Libraries Using a Consensus of Orthogonal Methodologies. Methods Mol. Biol. 2018, 1824, 261–277. [Google Scholar]
- Xia, J.; Hu, H.; Xue, W.; Wang, X.S.; Wu, S. The discovery of novel HDAC3 inhibitors via virtual screening and in vitro bioassay. J. Enzyme Inhib. Med. Chem. 2018, 33, 525–535. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Shi, D.; Zhou, S.; Liu, H.; Liu, H.; Yao, X. Molecular dynamics simulations and novel drug discovery. Expert Opin. Drug. Discov. 2018, 13, 23–37. [Google Scholar] [CrossRef]
- Chaput, L.; Mouawad, L. Efficient conformational sampling and weak scoring in docking programs? Strategy of the wisdom of crowds. J. Cheminform. 2017, 9, 37. [Google Scholar] [CrossRef]
- Wang, X.; Song, K.; Li, L.; Chen, L. Structure-Based Drug Design Strategies and Challenges. Curr. Top. Med. Chem. 2018, 18, 998–1006. [Google Scholar] [CrossRef]
- Li, G.B.; Yang, L.L.; Yuan, Y.; Zou, J.; Cao, Y.; Yang, S.Y.; Xiang, R.; Xiang, M. Virtual screening in small molecule discovery for epigenetic targets. Methods 2015, 71, 158–166. [Google Scholar] [CrossRef]
- Mavrogeni, M.E.; Pronios, F.; Zareifi, D.; Vasilakaki, S.; Lozach, O.; Alexopoulos, L.; Meijer, L.; Myrianthopoulos, V.; Mikros, E. A facile consensus ranking approach enhances virtual screening robustness and identifies a cell-active DYRK1α inhibitor. Future Med. Chem. 2018, 10, 2411–2430. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H.; Zheng, M.; Luo, J.; Kang, L.; Liu, X.; Wang, X.; Jiang, H. An effective docking strategy for virtual screening based on multi-objective optimization algorithm. BMC Bioinform. 2009, 10, 58. [Google Scholar] [CrossRef]
- Liu, S.; Fu, R.; Zhou, L.H.; Chen, S.P. Application of consensus scoring and principal component analysis for virtual screening against β-secretase (BACE-1). PLoS ONE 2012, 7, e38086. [Google Scholar] [CrossRef]
- Mazzolari, A.; Vistoli, G.; Testa, B.; Pedretti, A. Prediction of the Formation of Reactive Metabolites by A Novel Classifier Approach Based on Enrichment Factor Optimization (EFO) as Implemented in the VEGA Program. Molecules 2018, 23, 2955. [Google Scholar] [CrossRef]
- Huang, N.; Shoichet, B.K.; Irwin, J.J. Benchmarking sets for molecular docking. J. Med. Chem. 2006, 49, 6789–6801. [Google Scholar] [CrossRef]
- Harrison, R.W. Stiffness and energy conservation in the molecular dynamics-An improved integrator. J. Comp. Chem. 1993, 14, 1112–1122. [Google Scholar] [CrossRef]
- Wang, R.; Lai, L.; Wang, S. Further development and validation of empirical scoring functions for structure-based binding affinity prediction. J. Comput.-Aided. Mol. Des. 2002, 16, 11–26. [Google Scholar] [CrossRef]
- Pedretti, A.; Villa, L.; Vistoli, G. VEGA: A versatile program to convert, handle and visualize molecular structure on Windows-based PCs. J. Mol. Graph. Model 2002, 21, 47–49. [Google Scholar] [CrossRef]
- Vistoli, G.; Mazzolari, A.; Testa, B.; Pedretti, A. Binding Space Concept: A New Approach To Enhance the Reliability of Docking Scores and Its Application to Predicting Butyrylcholinesterase Hydrolytic Activity. J. Chem. Inf. Model 2017, 57, 1691–1702. [Google Scholar] [CrossRef] [PubMed]
- Gaillard, P.; Carrupt, P.A.; Testa, B.; Boudon, A. Molecular lipophilicity potential, a tool in 3D QSAR: Method and applications. J. Comput. Aided. Mol. Des. 1994, 8, 83–96. [Google Scholar] [CrossRef] [PubMed]
- Vistoli, G.; Pedretti, A.; Mazzolari, A.; Testa, B. Homology modeling and metabolism prediction of human carboxylesterase-2 using docking analyses by GriDock: A parallelized tool based on AutoDock 4.0. J. Comput. Aided. Mol. Des. 2010, 24, 771–787. [Google Scholar] [CrossRef] [PubMed]
- von Behren, M.M.; Rarey, M. Ligand-based virtual screening under partial shape constraints. J. Comput. Aided. Mol. Des. 2017, 31, 335–347. [Google Scholar] [CrossRef] [PubMed]
- Cang, Z.; Mu, L.; Wei, G.W. Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening. PLoS Comput. Biol. 2018, 14, e1005929. [Google Scholar] [CrossRef]
- Jasper, J.B.; Humbeck, L.; Brinkjost, T.; Koch, O. A novel interaction fingerprint derived from per atom score contributions: Exhaustive evaluation of interaction fingerprint performance in docking based virtual screening. J. Cheminform. 2018, 10, 15. [Google Scholar] [CrossRef]
- von Behren, M.M.; Bietz, S.; Nittinger, E.; Rarey, M. mRAISE: An alternative algorithmic approach to ligand-based virtual screening. J. Comput. Aided Mol. Des. 2016, 30, 583–594. [Google Scholar] [CrossRef]
- Korb, O.; Stützle, T.; Exner, T.E. Empirical scoring functions for advanced protein-ligand docking with PLANTS. J. Chem. Inf. Model 2009, 49, 84–96. [Google Scholar] [CrossRef]
- Stűtzle, T.; Hoos, H.H. MAX–MIN Ant System. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Pedretti, A.; Granito, C.; Mazzolari, A.; Vistoli, G. Structural Effects of Some Relevant Missense Mutations on the MECP2-DNA Binding: A MD Study Analyzed by Rescore+, a Versatile Rescoring Tool of the VEGA ZZ Program. Mol. Inform. 2016, 35, 424–433. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Vistoli, G.; Pedretti, A.; Mazzolari, A.; Testa, B. In silico prediction of human carboxylesterase-1 (hCES1) metabolism combining docking analyses and MD simulations. Bioorg. Med. Chem. 2010, 18, 320–329. [Google Scholar] [CrossRef] [PubMed]

| Target Class | Score | EF 1% | EF 2% | EF 5% | EF 10% | EF 20% |
|---|---|---|---|---|---|---|
| Kinases | PLANTS | 6.4 | 4.3 | 2.8 | 1.9 | 1.5 |
| Metalloenzymes | 17.7 | 13.6 | 7.2 | 4.8 | 3.0 | |
| Nuclear hormone receptors | 17.5 | 12.3 | 7.7 | 5.3 | 3.3 | |
| Serine Proteases | 14.6 | 13.3 | 8.5 | 5.7 | 3.5 | |
| Other enzymes | 17.1 | 12.2 | 7.2 | 4.8 | 3.0 | |
| Overall mean | 14.6 | 10.7 | 6.4 | 4.3 | 2.7 | |
| Kinases | Rescore without minimization | 15.1 | 10.5 | 5.9 | 3.6 | 2.2 |
| Metalloenzymes | 27.5 | 16.2 | 7.3 | 4.2 | 2.5 | |
| Nuclear hormone receptors | 22.2 | 16.8 | 10.1 | 6.4 | 3.7 | |
| Serine Proteases | 26.1 | 18.0 | 10.9 | 7.1 | 4.1 | |
| Other enzymes | 21.7 | 15.5 | 8.2 | 5.2 | 3.2 | |
| Overall mean | 21.4 | 14.9 | 8.2 | 5.1 | 3.1 | |
| Kinases | Rescore with minimization | 18.4 | 12.3 | 7.1 | 4.4 | 2.6 |
| Metalloenzymes | 26.3 | 16.0 | 7.4 | 4.2 | 2.5 | |
| Nuclear hormone receptors | 23.6 | 17.9 | 10.3 | 6.2 | 3.6 | |
| Serine Proteases | 27.1 | 19.7 | 13.6 | 8.0 | 4.4 | |
| Other enzymes | 24.4 | 17.1 | 10.2 | 6.0 | 3.5 | |
| Overall mean | 23.4 | 16.3 | 9.5 | 5.7 | 3.3 |
| Target Class | Score | EF 1% | EF 2% | EF 5% | EF 10% | EF 20% |
|---|---|---|---|---|---|---|
| Kinases | PLANTS | 9.0 | 6.4 | 4.0 | 3.0 | 2.0 |
| Metalloenzymes | 14.4 | 10.3 | 6.3 | 4.3 | 3.0 | |
| Nuclear hormone receptors | 22.9 | 16.4 | 9.0 | 5.7 | 3.5 | |
| Serine Proteases | 16.5 | 14.1 | 8.3 | 5.1 | 3.2 | |
| Other enzymes | 12.6 | 9.1 | 5.8 | 4.1 | 2.7 | |
| Overall mean | 15.1 | 11.3 | 6.7 | 4.4 | 2.9 | |
| Two vs. one variable | +0.5 | +0.6 | +0.3 | +0.1 | +0.2 | |
| Kinases | Rescore without minimization | 15.3 | 10.6 | 5.9 | 3.6 | 2.1 |
| Metalloenzymes | 24.4 | 18.3 | 10.0 | 6.3 | 4.0 | |
| Nuclear hormone receptors | 24.4 | 21.1 | 12.2 | 7.4 | 4.1 | |
| Serine Proteases | 27.3 | 19.1 | 11.9 | 7.0 | 4.2 | |
| Other enzymes | 24.2 | 17.0 | 9.6 | 6.1 | 3.5 | |
| Overall mean | 23.1 | 17.2 | 9.9 | 5.7 | 3.6 | |
| Two vs. one variable | +1.6 | +2.3 | +1.7 | +0.6 | +0.5 | |
| Kinases | Rescore with minimization | 23.5 | 16.5 | 8.7 | 5.1 | 2.8 |
| Metalloenzymes | 29.3 | 20.2 | 10.8 | 5.9 | 3.7 | |
| Nuclear hormone receptors | 25.4 | 20.9 | 12.2 | 7.0 | 3.9 | |
| Serine Proteases | 31.7 | 26.9 | 15.2 | 8.1 | 4.4 | |
| Other enzymes | 24.7 | 18.8 | 10.8 | 6.2 | 3.5 | |
| Overall mean | 26.9 | 20.7 | 11.5 | 6.5 | 3.7 | |
| Two vs. one variable | +3.5 | +4.4 | +2.0 | +0.8 | +0.4 | |
| Kinases | VEGA with minimization | 12.5 | 9.1 | 8.9 | 5.8 | 3.4 |
| Metalloenzymes | 12.0 | 12.4 | 9.6 | 6.4 | 3.6 | |
| Nuclear hormone receptors | 20.4 | 18.2 | 10.8 | 6.8 | 3.7 | |
| Serine Proteases | 18.6 | 15.9 | 10.1 | 5.9 | 3.3 | |
| Other enzymes | 13.9 | 11.8 | 8.2 | 5.4 | 3.4 | |
| Overall mean | 15.5 | 13.5 | 9.5 | 6.1 | 3.5 |
| Target Class | Score | EF 1% | EF 2% | EF 5% | EF 10% | EF 20% |
|---|---|---|---|---|---|---|
| Kinases | Rescore without minimization | 21.8 | 15.3 | 7.7 | 4.4 | 2.7 |
| Metalloenzymes | 19.3 | 12.0 | 8.1 | 5.0 | 3.2 | |
| Nuclear hormone receptors | 30.2 | 21.5 | 12.3 | 7.5 | 4.5 | |
| Serine Proteases | 29.9 | 23.3 | 14.4 | 8.1 | 4.9 | |
| Other enzymes | 24.2 | 17.9 | 9.6 | 5.8 | 3.3 | |
| Overall mean | 25.1 | 18.0 | 10.4 | 6.2 | 3.7 | |
| Three vs. one variable | +3.7 | +3.1 | +2.2 | +1.1 | +0.6 | |
| Three vs. two variables | +2 | +0.8 | +0.5 | +0.5 | +0.1 | |
| Kinases | Rescore with minimization | 20.5 | 15.2 | 8.2 | 5.0 | 3.0 |
| Metalloenzymes | 26.4 | 21.1 | 13.2 | 7.4 | 4.0 | |
| Nuclear hormone receptors | 34.4 | 28.5 | 16.4 | 9.3 | 4.9 | |
| Serine Proteases | 33.0 | 26.8 | 15.8 | 8.4 | 4.3 | |
| Other enzymes | 26.1 | 20.4 | 11.8 | 7.0 | 3.9 | |
| Overall mean | 28.1 | 22.4 | 13.1 | 7.4 | 4.0 | |
| Three vs. one variable | +4.7 | +6.1 | +3.6 | +1.7 | +0.7 | |
| Three vs. two variables | +1.2 | +1.7 | +1.6 | +0.9 | +0.3 |
| DUD Name | Protein class | EFO I | EFO II | EFO III | ΔAUC | PADIF | mRAISE | ML |
|---|---|---|---|---|---|---|---|---|
| CDK2 | Kinases | 0.78 | 0.82 | 0.82 | 0.04 | 0.81 | 0.67 | 0.88 |
| EGFr | Kinases | 0.67 | 0.68 | 0.70 | 0.03 | 0.91 | 0.96 | 0.95 |
| FGFr1 | Kinases | 0.86 | 0.88 | 0.97 | 0.11 | 0.49 | 0.54 | 0.95 |
| HSP90 | Kinases | 0.71 | 0.72 | 0.72 | 0.01 | 0.60 | 0.80 | 0.93 |
| P38 MAP | Kinases | 0.62 | 0.77 | 0.77 | 0.15 | 0.68 | 0.34 | 0.94 |
| PDGFrb | Kinases | 0.53 | 0.57 | 0.64 | 0.11 | n.a. | 0.35 | 0.97 |
| SRC | Kinases | 0.62 | 0.72 | 0.84 | 0.22 | 0.70 | 0.45 | 0.98 |
| TK | Kinases | 0.66 | 0.96 | 0.96 | 0.30 | 0.71 | 0.88 | 0.65 |
| VEGFr2 | Kinases | 0.66 | 0.72 | 0.72 | 0.06 | 0.60 | 0.44 | 0.96 |
| Mean | Kinases | 0.68 | 0.76 | 0.79 | 0.11 | 0.69 | 0.60 | 0.91 |
| ACE | Metalloenzymes | 0.68 | 0.74 | 0.77 | 0.09 | 0.46 | 0.91 | 0.81 |
| ADA | Metalloenzymes | 0.79 | 0.91 | 0.91 | 0.12 | 0.90 | 0.73 | 0.90 |
| COMT | Metalloenzymes | 0.52 | 0.74 | 0.99 | 0.47 | 0.63 | 0.85 | 0.73 |
| PDE5 | Metalloenzymes | 0.74 | 0.82 | 0.79 | 0.05 | 0.70 | 0.61 | 0.86 |
| Mean | Metalloenzymes | 0.68 | 0.80 | 0.87 | 0.18 | 0.67 | 0.78 | 0.83 |
| AR | NHR | 0.69 | 0.78 | 0.83 | 0.14 | 0.61 | 0.89 | 0.90 |
| ER agonist | NHR | 0.79 | 0.81 | 0.81 | 0.02 | 0.83 | 0.94 | 0.81 |
| ER antagonist | NHR | 0.87 | 0.86 | 0.97 | 0.10 | 0.93 | 0.92 | 0.83 |
| GR | NHR | 0.75 | 0.79 | 0.80 | 0.05 | 0.47 | 0.67 | 0.84 |
| MR | NHR | 0.77 | 0.94 | 0.97 | 0.20 | 0.81 | 0.85 | 0.87 |
| PPAR | NHR | 0.79 | 0.85 | 0.85 | 0.06 | 0.50 | 0.96 | 0.72 |
| PR | NHR | 0.73 | 0.77 | 0.79 | 0.06 | 0.72 | 0.71 | 0.91 |
| RXRa | NHR | 0.99 | 0.99 | 0.99 | 0.00 | 0.93 | 0.90 | 0.83 |
| Mean | NHR | 0.80 | 0.85 | 0.88 | 0.08 | 0.73 | 0.86 | 0.84 |
| FXa | Serine proteases | 0.85 | 0.88 | 0.88 | 0.03 | 0.67 | 0.71 | 0.89 |
| Thrombin | Serine proteases | 0.86 | 0.98 | 0.99 | 0.13 | 0.83 | 0.68 | 0.79 |
| Trypsin | Serine proteases | 0.97 | 0.98 | 0.99 | 0.02 | 0.95 | 0.68 | 0.78 |
| Mean | Serine proteases | 0.89 | 0.95 | 0.95 | 0.06 | 0.82 | 0.69 | 0.82 |
| AChE | Other enzymes | 0.71 | 0.71 | 0.77 | 0.06 | 0.65 | 0.75 | 0.65 |
| ALR2 | Other enzymes | 0.66 | 0.70 | 0.68 | 0.02 | 0.54 | 0.61 | 0.68 |
| AmpC | Other enzymes | 0.62 | 0.91 | 0.93 | 0.31 | 0.53 | 0.91 | 0.58 |
| COX-1 | Other enzymes | 0.66 | 0.68 | 0.72 | 0.06 | 0.39 | 0.59 | 0.86 |
| COX-2 | Other enzymes | 0.93 | 0.92 | 0.92 | -0.01 | 0.83 | 0.94 | 0.97 |
| GPB | Other enzymes | 0.91 | 0.92 | 0.93 | 0.02 | 0.88 | 0.92 | 0.66 |
| HIVPR | Other enzymes | 0.81 | 0.82 | 0.82 | 0.01 | 0.56 | 0.65 | 0.91 |
| HIVRT | Other enzymes | 0.70 | 0.75 | 0.81 | 0.11 | 0.56 | 0.64 | 0.88 |
| HMGR | Other enzymes | 0.64 | 0.77 | 0.71 | 0.07 | 0.87 | 0.95 | 0.96 |
| InhA | Other enzymes | 0.64 | 0.89 | 0.89 | 0.25 | 0.77 | 0.58 | 0.95 |
| NA | Other enzymes | 0.88 | 0.89 | 0.89 | 0.01 | 0.93 | 0.99 | 0.87 |
| PARP | Other enzymes | 0.86 | 0.96 | 0.96 | 0.10 | 0.74 | 0.63 | 0.71 |
| PNP | Other enzymes | 0.77 | 0.92 | 0.94 | 0.17 | 0.78 | 0.99 | 0.89 |
| SAHH | Other enzymes | 0.94 | 0.97 | 0.98 | 0.04 | 0.97 | 0.98 | 0.84 |
| DHFR | Other enzymes | 0.99 | 0.99 | 0.99 | 0.00 | 0.91 | 0.99 | 0.96 |
| GART | Other enzymes | 0.96 | 0.99 | 0.99 | 0.03 | 0.96 | 0.95 | 0.48 |
| Mean | Other enzymes | 0.79 | 0.86 | 0.87 | 0.08 | 0.74 | 0.82 | 0.80 |
| Overall mean | 0.76 | 0.84 | 0.86 | 0.10 | 0.73 | 0.76 | 0.84 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedretti, A.; Mazzolari, A.; Gervasoni, S.; Vistoli, G. Rescoring and Linearly Combining: A Highly Effective Consensus Strategy for Virtual Screening Campaigns. Int. J. Mol. Sci. 2019, 20, 2060. https://doi.org/10.3390/ijms20092060
Pedretti A, Mazzolari A, Gervasoni S, Vistoli G. Rescoring and Linearly Combining: A Highly Effective Consensus Strategy for Virtual Screening Campaigns. International Journal of Molecular Sciences. 2019; 20(9):2060. https://doi.org/10.3390/ijms20092060
Chicago/Turabian StylePedretti, Alessandro, Angelica Mazzolari, Silvia Gervasoni, and Giulio Vistoli. 2019. "Rescoring and Linearly Combining: A Highly Effective Consensus Strategy for Virtual Screening Campaigns" International Journal of Molecular Sciences 20, no. 9: 2060. https://doi.org/10.3390/ijms20092060
APA StylePedretti, A., Mazzolari, A., Gervasoni, S., & Vistoli, G. (2019). Rescoring and Linearly Combining: A Highly Effective Consensus Strategy for Virtual Screening Campaigns. International Journal of Molecular Sciences, 20(9), 2060. https://doi.org/10.3390/ijms20092060