Structure of Nanotubes Self-Assembled from a Monoamide Organogelator
Abstract
:1. Introduction
2. Results
2.1. Solubility and Gelation
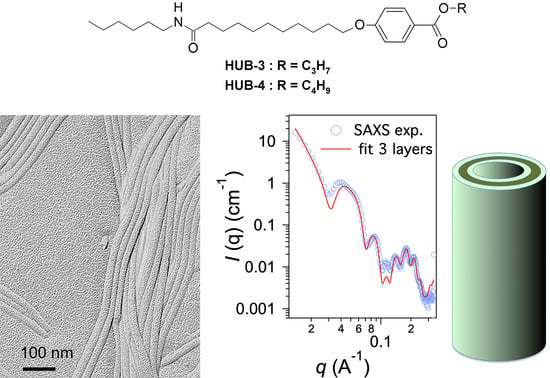
2.2. Structural Studies by Electron Microscopy
2.3. Structural Studies by SAXS
3. Discussion
4. Materials and Methods
4.1. Compounds
4.2. Characterisation of the Synthesized Compounds
4.3. FTIR of the Gels
4.4. Electron Microscopy
4.5. X-Ray Scattering
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SAXS | Small-angle X-ray scattering |
| SANS | Small-angle neutron scattering |
References
- Schnur, J.M. Lipid Tubules: A Paradigm for molecularly engineered structures. Science 1993, 262, 1669–1676. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, T.; Masuda, M.; Minamikawa, H. Supramolecular nanotube architectures based on Amphiphilic molecules. Chem. Rev. 2005, 105, 1401–1444. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, T. Self-assembly of discrete organic nanotubes. Bull. Chem. Soc. Jpn. 2018, 91, 623–668. [Google Scholar] [CrossRef]
- Helfrich, W. Helical bilayer structures due to spontaneous torsion of the edges. J. Chem. Phys. 1986, 85, 1085–1087. [Google Scholar] [CrossRef]
- Seifert, U.; Shillcock, J.; Nelson, P. Role of bilayer tilt difference in equilibrium membrane shapes. Phys. Rev. Lett. 1996, 77, 5237–5240. [Google Scholar] [CrossRef] [Green Version]
- Selinger, J.V.; Schnur, J.M. Theory of chiral lipid tubules. Phys. Rev. Lett. 1993, 71, 4091–4094. [Google Scholar] [CrossRef] [PubMed]
- Selinger, J.V.; Spector, M.S.; Schnur, J.M. Theory of self-assembled tubules and helical ribbons. J. Phys. Chem. B 2001, 105, 7157–7169. [Google Scholar] [CrossRef]
- Selinger, J.V.; MacKintosh, F.C.; Schnur, J.M. Theory of cylindrical tubules and helical ribbons of chiral lipid membranes. Phys. Rev. E 1996, 53, 3804–3818. [Google Scholar] [CrossRef] [Green Version]
- Chung, D.S.; Benedek, G.B.; Konikoff, F.M.; Donovan, J.M. Elastic free energy of anisotropic helical ribbons as metastable intermediates in the crystallization of cholesterol. Proc. Natl. Acad. Sci. USA 1993, 90, 11341–11345. [Google Scholar] [CrossRef] [Green Version]
- Nyrkova, I.A.; Semenov, A.N. Twisted surfactant structures: An advanced theoretical model. Soft Matter 2010, 6, 501–516. [Google Scholar] [CrossRef]
- Nyrkova, I.A.; Semenov, A.N. Self-assembling helical structures in solutions of achiral diamide-ester gelator molecules. Polymer 2018, 145, 202–231. [Google Scholar] [CrossRef]
- Oda, R.; Huc, I.; Schmutz, M.; Candau, S.J.; MacKintosh, F.C. Tuning bilayer twist using chiral counterions. Nature 1999, 399, 566–569. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, T.; Kogiso, M.; Masuda, M. Vesicle assembly in microtubes. Nature 1996, 383, 487–488. [Google Scholar] [CrossRef]
- Sirieix, J.; de Viguerie, N.L.; Rivière, M.; Lattes, A. From unsymmetrical bolaamphiphiles to supermolecules. New J. Chem. 2000, 24, 1043–1048. [Google Scholar] [CrossRef]
- Perino, A.; Schmutz, M.; Meunier, S.; Mésini, P.J.; Wagner, A. Self-Assembled Nanotubes and Helical Tapes from Diacetylene Nonionic Amphiphiles. Structural studies before and after polymerization. Langmuir 2011, 27, 12149–12155. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.B.; Koepsel, R.; Stolz, D.B.; Warriner, H.E.; Russell, A.J. Self-assembly of biocidal nanotubes from a single-chain diacetylene amine salt. J. Am. Chem. Soc. 2004, 126, 13400–13405. [Google Scholar] [CrossRef]
- Valéry, C.; Paternostre, M.; Robert, B.; Gulik-Krzywicki, T.; Narayanan, T.; Dedieu, J.-C.; Keller, G.; Torres, M.-L.; Cherif-Cheikh, R.; Calvo, P.; et al. Biomimetic organization: Octapeptide self-assembly into nanotubes of viral capsid-like dimension. Proc. Natl. Acad. Sci. USA 2003, 100, 10258–10262. [Google Scholar] [CrossRef] [Green Version]
- Oda, R.; Artzner, F.; Laguerre, M.; Huc, I. Molecular structure of self-assembled chiral nanoribbons and nanotubules revealed in the hydrated state. J. Am. Chem. Soc. 2008, 130, 14705–14712. [Google Scholar] [CrossRef]
- Schmutz, M.; Mésini, P.J. Cryo-fracture of self assembled systems in organic solvents. In Handbook of Cryopreparation Methods for Electron Microscopy; Cavalier, A., Spehner, D., Humbel, B.M., Eds.; Francis and Taylor CRC Press: New York, NY, USA, 2008; pp. 411–430. [Google Scholar]
- Nguyen, T.-T.-T.; Simon, F.-X.; Schmutz, M.; Mésini, P.J. Direct functionalization of self-assembled nanotubes overcomes unfavorable self-assembling processes. Chem. Commun. 2009, 3457–3459. [Google Scholar] [CrossRef]
- Engelkamp, H.; Middelbeek, S.; Nolte, R.J.M. Self-assembly of disk-shaped molecules to coiled-coil aggregates with tunable helicity. Science 1999, 284, 785–788. [Google Scholar] [CrossRef]
- Nguyen, T.-T.-T.; Simon, F.-X.; Combet, J.; Schmutz, M.; Mésini, P.J. Modification of self-assembled nanotubes by click chemistry generates new nanotubes by an out-of equilibrium process. Soft Matter 2011, 7, 1121–1128. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Te Nijenhuis, K. Chapter 4—Volumetric properties. In Properties of Polymers, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 71–108. ISBN 978-0-08-054819-7. [Google Scholar]
- Simon, F.-X.; Nguyen, T.T.T.; Díaz, N.; Schmutz, M.; Demé, B.; Jestin, J.; Combet, J.; Mésini, P.J. Self-assembling properties of a series of homologous ester-diamides—From ribbons to nanotubes. Soft Matter 2013, 9, 8483–8493. [Google Scholar] [CrossRef]
- Fuhrhop, J.H.; Schnieder, P.; Rosenberg, J.; Boekema, E. The chiral bilayer effect stabilizes micellar fibers. J. Am. Chem. Soc. 1987, 109, 3387–3390. [Google Scholar] [CrossRef] [Green Version]
- Guterman, T.; Levin, M.; Kolusheva, S.; Levy, D.; Noor, N.; Roichman, Y.; Gazit, E. Real-time in-situ monitoring of a tunable Pentapeptide Gel–Crystal transition. Angew. Chem. Int. Ed. 2019, 58, 15869–15875. [Google Scholar] [CrossRef] [PubMed]
- Huetz, P.; van Neuren, S.; Ringler, P.; Kremer, F.; van Breemen, J.F.L.; Wagenaar, A.; Engberts, J.B.F.N.; Fraaije, J.G.E.M.; Brisson, A. Relationship between molecular structure and supramolecular morphology of DODA-EO2-biotin and related lipids. Chem. Phys. Lipids 1997, 89, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Gubitosi, M.; D’Annibale, A.; Schillén, K.; Olsson, U.; Pavel, N.V.; Galantini, L. On the stability of lithocholate derivative supramolecular tubules. RSC Adv. 2016, 7, 512–517. [Google Scholar] [CrossRef] [Green Version]
- González, J.A.; Cobos, J.C.; De La Fuente, I.G. Thermodynamics of binary mixtures containing N-alkylamides. J. Mol. Liq. 2004, 115, 93–103. [Google Scholar] [CrossRef]
- Christ, E.; Blanc, C.; Al Ouahabi, A.; Maurin, D.; Le Parc, R.; Bantignies, J.-L.; Guenet, J.-M.; Collin, D.; Mésini, P.J. Origin of invariant gel melting temperatures in the C–T phase diagram of an Organogel. Langmuir 2016, 32, 4975–4982. [Google Scholar] [CrossRef]
- Kline, S.R. Reduction and analysis of SANS and USANS data using IGOR Pro. J. Appl. Crystallogr. 2006, 39, 895–900. [Google Scholar] [CrossRef]










| Parameters | Fit 1 | Fit 2 |
|---|---|---|
| e1 (Å) | 10.4 | 6.2 |
| e2 (Å) | 23.1 | 28.6 |
| e3 (Å) | 10.4 | 6.2 |
| total wall thickness (Å) | 43.9 | 41.0 |
| r4 (Å) | 53.2 | 55.0 |
| ρ1 (× 1010 cm−2) | 11.21 | 12.81 |
| ρ2 (× 1010 cm−2) | 8.84 | 8.65 |
| ρ3 (× 1010 cm−2) | 11.21 | 11.85 |
| ρs (× 1010 cm−2) | 7.55 | 7.55 |
| α | 1 | 1.07 |
| Δr4 (Å) | 3.3 | 3.4 |
| background (cm−1) | 0.0015 | 0.0015 |
| outer diameter (nm) | 19.4 | 19.2 |
| center-to-center dist. (nm) | 19.4 | 20.5 |
| Part of the Molecule | Estimated Density a (g/cm3) | Scattering Length Density (× 1010 cm−2) |
|---|---|---|
| Amide chains b | 1.04 | 9.92 |
| O–C6H4–COO– b | 1.55 | 19.63 |
| –C4H9 c | 0.81 | 7.90 |
| OC6H4COOC4H9 | 1.23 | 11.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zapién-Castillo, S.; Díaz-Zavala, N.P.; Melo-Banda, J.A.; Schwaller, D.; Lamps, J.-P.; Schmutz, M.; Combet, J.; Mésini, P.J. Structure of Nanotubes Self-Assembled from a Monoamide Organogelator. Int. J. Mol. Sci. 2020, 21, 4960. https://doi.org/10.3390/ijms21144960
Zapién-Castillo S, Díaz-Zavala NP, Melo-Banda JA, Schwaller D, Lamps J-P, Schmutz M, Combet J, Mésini PJ. Structure of Nanotubes Self-Assembled from a Monoamide Organogelator. International Journal of Molecular Sciences. 2020; 21(14):4960. https://doi.org/10.3390/ijms21144960
Chicago/Turabian StyleZapién-Castillo, Samuel, Nancy P. Díaz-Zavala, José A. Melo-Banda, Duncan Schwaller, Jean-Philippe Lamps, Marc Schmutz, Jérôme Combet, and Philippe J. Mésini. 2020. "Structure of Nanotubes Self-Assembled from a Monoamide Organogelator" International Journal of Molecular Sciences 21, no. 14: 4960. https://doi.org/10.3390/ijms21144960
APA StyleZapién-Castillo, S., Díaz-Zavala, N. P., Melo-Banda, J. A., Schwaller, D., Lamps, J. -P., Schmutz, M., Combet, J., & Mésini, P. J. (2020). Structure of Nanotubes Self-Assembled from a Monoamide Organogelator. International Journal of Molecular Sciences, 21(14), 4960. https://doi.org/10.3390/ijms21144960