Brownian Motion Influence on AFM Exosomes’ Size Measurements
Abstract
:1. Introduction
2. Results
2.1. Measurements of Vesicles’ Geometric Diameters
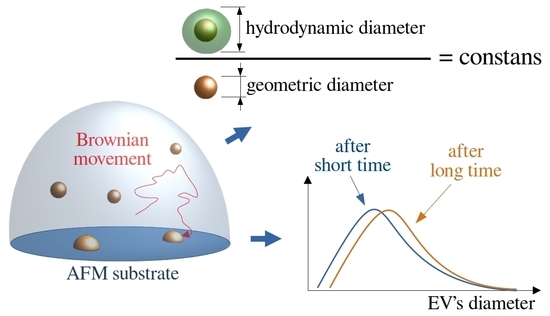
2.2. Simulations of Brownian Movement in a Specimen Drop
2.3. Lognormal Distribution
2.4. Hypothetical Bimodal Distribution
3. Discussion
4. Materials and Methods
4.1. Extracellular Vesicle Preparation
4.2. Nanoparticle Tracking Analysis (NTA)
4.3. Atomic Force Microscopy (AFM)
4.4. AFM Image Analysis
4.5. Simulations of Brownian Movement in a Specimen Drop
5. Conclusions
- (i)
- A reasonable compromise should be made between droplet thickness and waiting time before AFM imaging. Based on the results presented in Figure 3, it can be assumed that a drop 0.5 mm thick (with sufficient vesicles concentration) and time before imaging 5–10 h (with adequate humidity so that the sample would not dry during this time) will allow obtaining a representative statistical sample of vesicles attached to the mica substrate.
- (ii)
- It is suggested as an additional method of characterizing the physical properties of EVs to find the ratio of the hydrodynamic diameter to the geometric diameter. For this purpose, on the basis of AFM imaging, a histogram of geometric diameters of the vesicles should be created (see Section 4.4), and a histogram of the hydrodynamic diameters should be obtained using NTA. If fitting the log-normal distributions to this data, you obtain , then the quantity you are looking for will be the ratio .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EVs | extracelular vesicles |
| AFM | Atomic Force Microscopy |
| NTA | Nanoparticle Tracking Analysis |
| FBS | fetal bovine serum |
| APTES | 3-aminopropyltriethoxysilane |
| FWHM | full width at half maximum |
| CI | confidence interval |
References
- Olejarz, W.; Kubiak-Tomaszewska, G.; Chrzanowska, A.; Lorenc, T. Exosomes in Angiogenesis and Anti-angiogenic Therapy in Cancers. Int. J. Mol. Sci. 2020, 21, 5840. [Google Scholar] [CrossRef]
- Olejarz, W.; Dominiak, A.; Żołnierzak, A.; Kubiak-Tomaszewska, G.; Lorenc, T. Tumor-Derived Exosomes in Immunosuppression and Immunotherapy. J. Immunol. Res. 2020, 2020, 6272498. [Google Scholar] [CrossRef] [PubMed]
- Lorenc, T.; Klimczyk, K.; Michalczewska, I.; Slomka, M.; Kubiak-Tomaszewska, G.; Olejarz, W. Exosomes in Prostate Cancer Diagnosis, Prognosis and Therapy. Int. J. Mol. Sci. 2020, 21, 2118. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Pang, B.; Li, J.; Gao, N.; Fan, T.; Li, Y. Emerging Role of Exosomes in Liquid Biopsy for Monitoring Prostate Cancer Invasion and Metastasis. Front. Cell Dev. Biol. 2021, 9, 679527. [Google Scholar] [CrossRef]
- Tang, X.; Shi, X.; Gan, Y.; Yi, X. Nanomechanical characterization of pressurized elastic fluid nanovesicles using indentation analysis. Extrem. Mech. Lett. 2019, 34, 100613. [Google Scholar] [CrossRef]
- Vorselen, D.; van Dommelen, S.M.; Sorkin, R.; Piontek, M.C.; Schiller, J.; Dopp, S.T.; Kooijmans, S.A.A.; van Oirschot, B.A.; Versluijs, B.A.; Bierings, M.B.; et al. The fluid membrane determines mechanics of erythrocyte extracellular vesicles and is softened in hereditary spherocytosis. Nat. Commun. 2018, 9, 4960. [Google Scholar] [CrossRef]
- Lorenc, T.; Chrzanowski, J.; Olejarz, W. Current Perspectives on Clinical Use of Exosomes as a Personalized Contrast Media and Theranostics. Cancers 2020, 12, 3386. [Google Scholar] [CrossRef]
- Anselmo, A.C.; Zhang, M.; Kumar, S.; Vogus, D.R.; Menegatti, S.; Helgeson, M.E.; Mitragotri, S. Elasticity of Nanoparticles Influences Their Blood Circulation, Phagocytosis, Endocytosis, and Targeting. ACS Nano 2015, 9, 3169–3177. [Google Scholar] [CrossRef]
- Anselmo, A.C.; Mitragotri, S. Impact of particle elasticity on particle-based drug delivery systems. Adv. Drug Deliv. Rev. 2017, 108, 51–67. [Google Scholar] [CrossRef]
- LeClaire, M.; Gimzewski, J.; Sharma, S. A review of the biomechanical properties of single extracellular vesicles. Nano Select 2021, 2, 1–15. [Google Scholar] [CrossRef]
- Vorselen, D.; Piontek, M.C.; Roos, W.H.; Wuite, G. Mechanical Characterization of Liposomes and Extracellular Vesicles, a Protocol. Front. Mol. Biosci. 2020, 7, 139. [Google Scholar] [CrossRef] [PubMed]
- Théry, C.; Witwer, K.W.; Aikawa, E.; Alcaraz, M.J.; Anderson, J.D.; Andriantsitohaina, R.; Antoniou, A.; Arab, T.; Archer, F.; Atkin-Smith, G.K.; et al. Minimal information for studies of extracellular vesicles 2018 (MISEV2018): A position statement of the International Society for Extracellular Vesicles and update of the MISEV2014 guidelines. J. Extracell. Vesicles 2018, 7, 1535750. [Google Scholar] [CrossRef] [PubMed]
- Skliar, M.; Chernyshev, V.S. Imaging of Extracellular Vesicles by Atomic Force Microscopy. J. Vis. Exp. 2019, 151, e59254. [Google Scholar] [CrossRef]
- Chernyshev, V.S.; Rachamadugu, R.; Tseng, Y.H.; Belnap, D.M.; Jia, Y.; Branch, K.J.; Butterfield, A.E.; Pease, L.F., III; Bernard, P.S.; Skliar, M. Size and shape characterization of hydrated and desiccated exosomes. Anal. Bioanal. Chem. 2015, 407, 3285–3301. [Google Scholar] [CrossRef] [PubMed]
- Shringi, S.; Sharma, N.N. Analysis of Brownian particle considering nonrigidity of matter—A Langevin equation approach. In Proceedings of the 2017 IEEE 17th International Conference on Nanotechnology (IEEE-NANO), Pittsburgh, PA, USA, 25–28 July 2017; pp. 204–207. [Google Scholar] [CrossRef]
- Lisicki, M.; Velho Rodrigues, M.F.; Goldstein, R.E.; Lauga, E. Swimming eukaryotic microorganisms exhibit a universal speed distribution. eLife 2019, 8, e44907. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal Distributions across the Sciences: Keys and Clues: On the charms of statistics, and how mechanical models resembling gambling machines offer a link to a handy way to characterize log-normal distributions, which can provide deeper insight into variability and probability—Normal or log-normal: That is the question. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Mrowczynski, O.D.; Madhankumar, A.B.; Sundstrom, J.M.; Zhao, Y.; Imamura Kawasawa, Y.; Slagle-Webb, B.; Mau, C.; Payne, R.A.; Rizk, E.B.; Zacharia, B.E.; et al. Exosomes impact survival to radiation exposure in cell line models of nervous system cancer. Oncotarget 2018, 9, 36083–36101. [Google Scholar] [CrossRef] [PubMed]
- Bairamukov, V.; Bukatin, A.; Landa, S.; Burdakov, V.; Shtam, T.; Chelnokova, I.; Fedorova, N.; Filatov, M.; Starodubtseva, M. Biomechanical. Properties of Blood Plasma Extracellular Vesicles Revealed by Atomic Force Microscopy. Biology 2021, 10, 4. [Google Scholar] [CrossRef] [PubMed]
- Yurtsever, A.; Yoshida, T.; Badami Behjat, A.; Araki, Y.; Hanayama, R.; Fukuma, T. Structural and mechanical characteristics of exosomes from osteosarcoma cells explored by 3D-atomic force microscopy. Nanoscale 2021, 13, 6661–6677. [Google Scholar] [CrossRef]
- Ridolfi, A.; Brucale, M.; Montis, C.; Caselli, L.; Paolini, L.; Borup, A.; Boysen, A.T.; Loria, F.; van Herwijnen, M.J.C.; Kleinjan, M.; et al. AFM-Based High-Throughput Nanomechanical Screening of Single Extracellular Vesicles. Anal. Chem. 2020, 92, 10274–10282. [Google Scholar] [CrossRef]
- Needham, D.; Nunn, R.S. Elastic deformation and failure of lipid bilayer membranes containing cholesterol. Biophys. J. 1990, 58, 997–1009. [Google Scholar] [CrossRef]
- Skliar, M.; Chernyshev, V.S.; Belnap, D.M.; Sergey, G.V.; Al-Hakami, S.M.; Bernard, P.S.; Stijleman, I.J.; Rachamadugu, R. Membrane proteins significantly restrict exosome mobility. Biochem. Biophys. Res. Commun. 2018, 501, 1055–1059. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, N.; Hong, C.S.; Ludwig, S.; Azambuja, J.H.; Sharma, P.; Theodoraki, M.N.; Whiteside, T.L. Isolation and Analysis of Tumor-Derived Exosomes. Curr. Protoc. Immunol. 2019, 127, e91. [Google Scholar] [CrossRef] [PubMed]
- Pszczółkowska, B.; Olejarz, W.; Filipek, M.; Tartas, A.; Kubiak-Tomaszewska, G.; Żołnierzak, A.; Życieńska, K.; Ginter, J.; Lorenc, T.; Brzozowska, B. Exosome secretion and cellular response of DU145 and PC3 after exposure to alpha radiation. Radiat. Environ. Biophys. 2022, accepted. [Google Scholar]
- Kikuchi, Y.; Obana, N.; Toyofuku, M.; Kodera, N.; Soma, T.; Ando, T.; Fukumori, Y.; Nomura, N.; Taoka, A. Diversity of physical properties of bacterial extracellular membrane vesicles revealed through atomic force microscopy phase imaging. Nanoscale 2020, 12, 7950–7959. [Google Scholar] [CrossRef]
- Xu, K.; Sun, W.; Shao, Y.; Wei, F.; Zhang, X.; Wang, W.; Li, P. Recent development of PeakForce Tapping mode atomic force microscopy and its applications on nanoscience. Nanotechnol. Rev. 2018, 7, 605–621. [Google Scholar] [CrossRef]
- Regan, D.; Williams, J.; Borri, P.; Langbein, W. Lipid Bilayer Thickness Measured by Quantitative DIC Reveals Phase Transitions and Effects of Substrate Hydrophilicity. Langmuir ACS J. Surf. Colloids 2019, 35, 13805–13814. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Srivastava, R.; Khanna, K.N. Stokes-Einstein Relation in Two- and Three-Dimensional Fluids. J. Chem. Eng. Data 2009, 54, 1452–1456. [Google Scholar] [CrossRef]







| Scale (nm) | Shape (nm) | |
|---|---|---|
| geometric diameters AFM after 1 h | 71.1 [, +3.0] | 1.431 [, +0.033] |
| geometric diameters AFM after 20 h | 79.8 [, +4.7] | 1.436 [, +0.050] |
| hydrodynamic diameters NTA | 149.2 [, +2.3] | 1.461 [, +0.014] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Życieńska, K.; Pszczółkowska, B.; Brzozowska, B.; Kamiński, M.; Lorenc, T.; Olejarz, W.; Sęk, S.; Ginter, J. Brownian Motion Influence on AFM Exosomes’ Size Measurements. Int. J. Mol. Sci. 2022, 23, 10074. https://doi.org/10.3390/ijms231710074
Życieńska K, Pszczółkowska B, Brzozowska B, Kamiński M, Lorenc T, Olejarz W, Sęk S, Ginter J. Brownian Motion Influence on AFM Exosomes’ Size Measurements. International Journal of Molecular Sciences. 2022; 23(17):10074. https://doi.org/10.3390/ijms231710074
Chicago/Turabian StyleŻycieńska, Katarzyna, Beata Pszczółkowska, Beata Brzozowska, Maciej Kamiński, Tomasz Lorenc, Wioletta Olejarz, Sławomir Sęk, and Józef Ginter. 2022. "Brownian Motion Influence on AFM Exosomes’ Size Measurements" International Journal of Molecular Sciences 23, no. 17: 10074. https://doi.org/10.3390/ijms231710074
APA StyleŻycieńska, K., Pszczółkowska, B., Brzozowska, B., Kamiński, M., Lorenc, T., Olejarz, W., Sęk, S., & Ginter, J. (2022). Brownian Motion Influence on AFM Exosomes’ Size Measurements. International Journal of Molecular Sciences, 23(17), 10074. https://doi.org/10.3390/ijms231710074