AlphaFold2: A Role for Disordered Protein/Region Prediction?
Abstract
:1. Introduction
2. Methodology
2.1. Dataset Generation
2.2. Nrf2 Structure Generation
2.3. Molecular Dynamics Simulations
3. Results
3.1. pLDDT Performs Better Than Conventional Predictors and a Näive Use of DSSP for Disorder Identification
3.2. Sequence Predictors Can Still Outperform AlphaFold2 on Disorder Prediction
3.3. Secondary Structure Codons (SSC) Suggests Relationships between the pLDDT and Secondary Structure
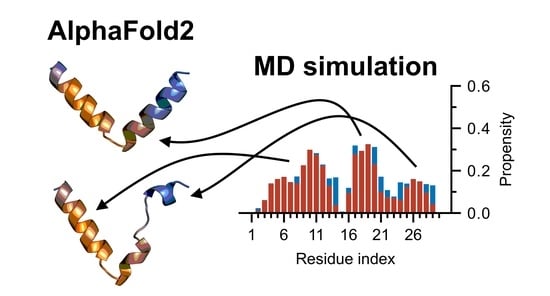
3.4. Nrf2: A Case Study
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dill, K.A.; MacCallum, J.L. The Protein-Folding Problem, 50 Years On. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nassar, R.; Dignon, G.L.; Razban, R.M.; Dill, K.A. The Protein Folding Problem: The Role of Theory. J. Mol. Biol. 2021, 433, 167126. [Google Scholar] [CrossRef] [PubMed]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Mullard, A. What does AlphaFold mean for drug discovery? Nat. Rev. Drug Discov. 2021, 20, 725–727. [Google Scholar] [CrossRef] [PubMed]
- Serpell, L.C.; Radford, S.E.; Otzen, D.E. AlphaFold: A Special Issue and A Special Time for Protein Science. J. Mol. Biol. 2021, 433, 167231. [Google Scholar] [CrossRef]
- Strodel, B. Energy Landscapes of Protein Aggregation and Conformation Switching in Intrinsically Disordered Proteins. J. Mol. Biol. 2021, 433, 167182. [Google Scholar] [CrossRef]
- Ruff, K.M.; Pappu, R.V. AlphaFold and Implications for Intrinsically Disordered Proteins. J. Mol. Biol. 2021, 433, 167208. [Google Scholar] [CrossRef]
- Akdel, M.; Pires, D.E.V.; Pardo, E.P.; Jänes, J.; Zalevsky, A.O.; Mészáros, B.; Bryant, P.; Good, L.L.; Laskowski, R.A.; Pozzati, G.; et al. A structural biology community assessment of AlphaFold 2 applications. bioRxiv 2021. [Google Scholar] [CrossRef]
- Buel, G.R.; Walters, K.J. Can AlphaFold2 predict the impact of missense mutations on structure? Nat. Struct. Mol. Biol. 2022, 29, 1–2. [Google Scholar] [CrossRef]
- Wright, P.E.; Dyson, H. Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. J. Mol. Biol. 1999, 293, 321–331. [Google Scholar] [CrossRef] [Green Version]
- Dunker, A.; Lawson, J.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh, J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W.; et al. Intrinsically disordered protein. J. Mol. Graph. Model. 2001, 19, 26–59. [Google Scholar] [CrossRef] [Green Version]
- Dunker, A.K.; Brown, C.J.; Lawson, J.D.; Iakoucheva, L.M.; Obradović, Z. Intrinsic Disorder and Protein Function. Biochemistry 2002, 41, 6573–6582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uversky, V.N. Intrinsically Disordered Proteins and Their “Mysterious” (Meta)Physics. Front. Phys. 2019, 7, 10. [Google Scholar] [CrossRef] [Green Version]
- DeForte, S.; Uversky, V.N. Intrinsically Disordered Proteins in PubMed: What can the tip of the iceberg tell us about what lies below? RSC Adv. 2016, 6, 11513–11521. [Google Scholar] [CrossRef]
- Lyle, N.; Das, R.K.; Pappu, R.V. A quantitative measure for protein conformational heterogeneity. J. Chem. Phys. 2013, 139, 121907. [Google Scholar] [CrossRef]
- Choi, U.B.; Sanabria, H.; Smirnova, T.; Bowen, M.E.; Weninger, K.R. Spontaneous Switching among Conformational Ensembles in Intrinsically Disordered Proteins. Biomolecules 2019, 9, 114. [Google Scholar] [CrossRef] [Green Version]
- Salem, A.; Wilson, C.J.; Rutledge, B.S.; Dilliott, A.; Farhan, S.; Choy, W.Y.; Duennwald, M.L. Matrin3: Disorder and ALS Pathogenesis. Front. Mol. Biosci. 2022, 8, 794646. [Google Scholar] [CrossRef]
- Turoverov, K.K.; Kuznetsova, I.M.; Uversky, V.N. The protein kingdom extended: Ordered and Intrinsically Disordered Proteins, their folding, supramolecular complex formation, and aggregation. Prog. Biophys. Mol. Biol. 2010, 102, 73–84. [Google Scholar] [CrossRef] [Green Version]
- Uversky, V.N. Unusual biophysics of Intrinsically Disordered Proteins. Biochim. Biophys. Acta Proteins Proteom. 2013, 1834, 932–951. [Google Scholar] [CrossRef]
- Fisher, C.K.; Stultz, C.M. Constructing ensembles for Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol. 2011, 21, 426–431. [Google Scholar] [CrossRef] [Green Version]
- Das, R.K.; Ruff, K.M.; Pappu, R.V. Relating sequence encoded information to form and function of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2015, 32, 102–112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, R.K.; Pappu, R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA 2013, 110, 13392–13397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, A.H.; Crick, S.L.; Vitalis, A.; Chicoine, C.L.; Pappu, R.V. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 8183–8188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Romero, P.; Obradovic, Z.; Li, X.; Garner, E.C.; Brown, C.J.; Dunker, A.K. Sequence complexity of disordered protein. Proteins Struct. Funct. Bioinf. 2001, 42, 38–48. [Google Scholar] [CrossRef]
- Radivojac, P.; Iakoucheva, L.M.; Oldfield, C.J.; Obradovic, Z.; Uversky, V.N.; Dunker, A.K. Intrinsic Disorder and Functional Proteomics. Biophys. J. 2007, 92, 1439–1456. [Google Scholar] [CrossRef] [Green Version]
- Theillet, F.X.; Kalmar, L.; Tompa, P.; Han, K.H.; Selenko, P.; Dunker, A.K.; Daughdrill, G.W.; Uversky, V.N. The alphabet of intrinsic disorder. Intrinsically Disord. Proteins 2013, 1, e24360. [Google Scholar] [CrossRef] [Green Version]
- Uversky, V.N. The alphabet of intrinsic disorder. Intrinsically Disord. Proteins 2013, 1, e24684. [Google Scholar] [CrossRef] [Green Version]
- Tunyasuvunakool, K.; Adler, J.; Wu, Z.; Green, T.; Zielinski, M.; Žídek, A.; Bridgland, A.; Cowie, A.; Meyer, C.; Laydon, A.; et al. Highly accurate protein structure prediction for the human proteome. Nature 2021, 596, 590–596. [Google Scholar] [CrossRef]
- Necci, M.; Piovesan, D.; CAID Predictors; DisProt Curators; Tosatto, S.C.E. Critical assessment of protein intrinsic disorder prediction. Nat. Methods 2021, 18, 472–481. [Google Scholar] [CrossRef]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef]
- Hatos, A.; Hajdu-Soltész, B.; Monzon, A.M.; Palopoli, N.; Álvarez, L.; Aykac-Fas, B.; Bassot, C.; Benítez, G.I.; Bevilacqua, M.; Chasapi, A.; et al. DisProt: Intrinsic protein disorder annotation in 2020. Nucleic Acids Res. 2019, 48, D269–D276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mariani, V.; Biasini, M.; Barbato, A.; Schwede, T. lDDT: A local superposition-free score for comparing protein structures and models using distance difference tests. Bioinformatics 2013, 29, 2722–2728. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, G.; Katuwawala, A.; Wang, K.; Wu, Z.; Ghadermarzi, S.; Gao, J.; Kurgan, L. flDPnn: Accurate intrinsic disorder prediction with putative propensities of disorder functions. Nat. Commun. 2021, 12, 4438. [Google Scholar] [CrossRef]
- Hanson, J.; Paliwal, K.K.; Litfin, T.; Zhou, Y. SPOT-Disorder2: Improved Protein Intrinsic Disorder Prediction by Ensembled Deep Learning. Genom. Proteom. Bioinform. 2019, 17, 645–656. [Google Scholar] [CrossRef]
- Mirabello, C.; Wallner, B. rawMSA: End-to-end Deep Learning using raw Multiple Sequence Alignments. PLoS ONE 2019, 14, e0220182. [Google Scholar] [CrossRef] [Green Version]
- Deng, X.; Eickholt, J.; Cheng, J. PreDisorder: ab initio sequence-based prediction of protein disordered regions. BMC Bioinform. 2009, 10, 436. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Ma, J.; Xu, J. AUCpreD: Proteome-level protein disorder prediction by AUC-maximized deep convolutional neural fields. Bioinformatics 2016, 32, i672–i679. [Google Scholar] [CrossRef]
- Hanson, J.; Yang, Y.; Paliwal, K.; Zhou, Y. Improving protein disorder prediction by deep bidirectional long short-term memory recurrent neural networks. Bioinformatics 2016, 33, 685–692. [Google Scholar] [CrossRef] [Green Version]
- Hanson, J.; Paliwal, K.; Zhou, Y. Accurate Single-Sequence Prediction of Protein Intrinsic Disorder by an Ensemble of Deep Recurrent and Convolutional Architectures. J. Chem. Inf. Model. 2018, 58, 2369–2376. [Google Scholar] [CrossRef] [Green Version]
- Orlando, G.; Raimondi, D.; Codice, F.; Tabaro, F.; Vranken, W. Prediction of disordered regions in proteins with recurrent Neural Networks and protein dynamics. bioRxiv 2020. [Google Scholar] [CrossRef]
- Walsh, I.; Martin, A.J.M.; Domenico, T.D.; Tosatto, S.C.E. ESpritz: Accurate and fast prediction of protein disorder. Bioinformatics 2011, 28, 503–509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Waskom, M.L. seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Mirdita, M.; Schütze, K.; Moriwaki, Y.; Heo, L.; Ovchinnikov, S.; Steinegger, M. ColabFold—Making protein folding accessible to all. bioRxiv 2021. [Google Scholar] [CrossRef]
- Chang, M.; Wilson, C.J.; Karunatilleke, N.C.; Moselhy, M.H.; Karttunen, M.; Choy, W.Y. Exploring the Conformational Landscape of the Neh4 and Neh5 Domains of Nrf2 Using Two Different Force Fields and Circular Dichroism. J. Chem. Theory Comput. 2021, 17, 3145–3156. [Google Scholar] [CrossRef]
- Karunatilleke, N.C.; Fast, C.S.; Ngo, V.; Brickenden, A.; Duennwald, M.L.; Konermann, L.; Choy, W.Y. Nrf2, the Major Regulator of the Cellular Oxidative Stress Response, is Partially Disordered. Int. J. Mol. Sci. 2021, 22, 7434. [Google Scholar] [CrossRef]
- Aliev, A.E.; Kulke, M.; Khaneja, H.S.; Chudasama, V.; Sheppard, T.D.; Lanigan, R.M. Motional timescale predictions by molecular dynamics simulations: Case study using proline and hydroxyproline sidechain dynamics. Proteins 2014, 82, 195–215. [Google Scholar] [CrossRef] [Green Version]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [Green Version]
- Best, R.B.; Hummer, G. Optimized Molecular Dynamics Force Fields Applied to the Helix-Coil Transition of Polypeptides. J. Phys. Chem. B 2009, 113, 9004–9015. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An Nlog (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef]
- Moi, P.; Chan, K.; Asunis, I.; Cao, A.; Kan, Y.W. Isolation of NF-E2-related factor 2 (Nrf2), a NF-E2-like basic leucine zipper transcriptional activator that binds to the tandem NF-E2/AP1 repeat of the beta-globin locus control region. Proc. Natl. Acad. Sci. USA 1994, 91, 9926–9930. [Google Scholar] [CrossRef] [Green Version]
- Katoh, Y.; Itoh, K.; Yoshida, E.; Miyagishi, M.; Fukamizu, A.; Yamamoto, M. Two domains of Nrf2 cooperatively bind CBP, a CREB binding protein, and synergistically activate transcription. Genes Cells 2001, 6, 857–868. [Google Scholar] [CrossRef]
- Zhang, J.; Hosoya, T.; Maruyama, A.; Nishikawa, K.; Maher, J.M.; Ohta, T.; Motohashi, H.; Fukamizu, A.; Shibahara, S.; Itoh, K.; et al. Nrf2 Neh5 domain is differentially utilized in the transactivation of cytoprotective genes. Biochem. J. 2007, 404, 459–466. [Google Scholar] [CrossRef] [Green Version]
- van der Lee, R.; Buljan, M.; Lang, B.; Weatheritt, R.J.; Daughdrill, G.W.; Dunker, A.K.; Fuxreiter, M.; Gough, J.; Gsponer, J.; Jones, D.T.; et al. Classification of Intrinsically Disordered Regions and Proteins. Chem. Rev. 2014, 114, 6589–6631. [Google Scholar] [CrossRef]
- Uversky, V.N. Recent Developments in the Field of Intrinsically Disordered Proteins: Intrinsic Disorder–Based Emergence in Cellular Biology in Light of the Physiological and Pathological Liquid–Liquid Phase Transitions. Annu. Rev. Biophys. 2021, 50, 135–156. [Google Scholar] [CrossRef] [PubMed]
- Miskei, M.; Horvath, A.; Vendruscolo, M.; Fuxreiter, M. Sequence-Based Prediction of Fuzzy Protein Interactions. J. Mol. Biol. 2020, 432, 2289–2303. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Mizianty, M.J.; Kurgan, L. Genome-scale prediction of proteins with long intrinsically disordered regions. Proteins 2013, 82, 145–158. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.; Sodhi, J.; McGuffin, L.; Buxton, B.; Jones, D. Prediction and Functional Analysis of Native Disorder in Proteins from the Three Kingdoms of Life. J. Mol. Biol. 2004, 337, 635–645. [Google Scholar] [CrossRef]
- Piovesan, D.; Necci, M.; Escobedo, N.; Monzon, A.M.; Hatos, A.; Mičetić, I.; Quaglia, F.; Paladin, L.; Ramasamy, P.; Dosztányi, Z.; et al. MobiDB: Intrinsically disordered proteins in 2021. Nucleic Acids Res. 2020, 49, D361–D367. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Liu, B. A comprehensive review and comparison of existing computational methods for intrinsically disordered protein and region prediction. Brief. Bioinform. 2017, 20, 330–346. [Google Scholar] [CrossRef]
- Wilson, C.J.; Choy, W.Y.; Karttunen, M. AlphaFold2: A role for disordered protein prediction? bioRxiv 2021. [Google Scholar] [CrossRef]
- Piovesan, D.; Monzon, A.M.; Tosatto, S.C. Intrinsic Protein Disorder, Conditional Folding and AlphaFold2. bioRxiv 2022. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Kragelund, B.B. On the Potential of Machine Learning to Examine the Relationship Between Sequence, Structure, Dynamics and Function of Intrinsically Disordered Proteins. J. Mol. Biol. 2021, 433, 167196. [Google Scholar] [CrossRef]
- Alderson, T.R.; Pritišanac, I.; Moses, A.M.; Forman-Kay, J.D. Systematic identification of conditionally folded intrinsically disordered regions by AlphaFold2. bioRxiv 2022. [Google Scholar] [CrossRef]
- Wright, P.E.; Dyson, H.J. Linking folding and binding. Curr. Opin. Struct. Biol. 2009, 19, 31–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freiberger, M.I.; Wolynes, P.G.; Ferreiro, D.U.; Fuxreiter, M. Frustration in Fuzzy Protein Complexes Leads to Interaction Versatility. J. Phys. Chem. B 2021, 125, 2513–2520. [Google Scholar] [CrossRef] [PubMed]
- Oldfield, C.J.; Dunker, A.K. Intrinsically Disordered Proteins and Intrinsically Disordered Protein Regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Multitude of binding modes attainable by Intrinsically Disorder Proteins: A portrait gallery of disorder-based complexes. Chem. Soc. Rev. 2011, 40, 1623–1634. [Google Scholar] [CrossRef] [PubMed]
- Sharma, R.; Raduly, Z.; Miskei, M.; Fuxreiter, M. Fuzzy complexes: Specific binding without complete folding. FEBS Lett. 2015, 589, 2533–2542. [Google Scholar] [CrossRef] [Green Version]
- Khan, H.; Cino, E.A.; Brickenden, A.; Fan, J.; Yang, D.; Choy, W.Y. Fuzzy Complex Formation between the Intrinsically Disordered Prothymosin α and the Kelch Domain of Keap1 Involved in the Oxidative Stress Response. J. Mol. Biol. 2013, 425, 1011–1027. [Google Scholar] [CrossRef] [Green Version]
- Tompa, P.; Fuxreiter, M. Fuzzy complexes: Polymorphism and structural disorder in protein–protein interactions. Trends Biochem. Sci. 2008, 33, 2–8. [Google Scholar] [CrossRef]
- Arbesú, M.; Iruela, G.; Fuentes, H.; Teixeira, J.M.C.; Pons, M. Intramolecular Fuzzy Interactions Involving Intrinsically Disordered Domains. Front. Mol. Biosci. 2018, 5, 39. [Google Scholar] [CrossRef] [Green Version]
- Killoran, R.C.; Sowole, M.A.; Halim, M.A.; Konermann, L.; Choy, W.Y. Conformational characterization of the intrinsically disordered protein Chibby: Interplay between structural elements in target recognition. Protein Sci. 2016, 25, 1420–1429. [Google Scholar] [CrossRef] [Green Version]
- Gall, C.; Xu, H.; Brickenden, A.; Ai, X.; Choy, W.Y. The intrinsically disordered TC-1 interacts with Chibby via regions with high helical propensity. Protein Sci. 2007, 16, 2510–2518. [Google Scholar] [CrossRef] [Green Version]
- Mokhtarzada, S.; Yu, C.; Brickenden, A.; Choy, W.Y. Structural Characterization of Partially Disordered Human Chibby: Insights into Its Function in the Wnt-Signaling Pathway. Biochemistry 2011, 50, 715–726. [Google Scholar] [CrossRef] [PubMed]
- Zahn, R.; Liu, A.; Luhrs, T.; Riek, R.; von Schroetter, C.; Garcia, F.L.; Billeter, M.; Calzolai, L.; Wider, G.; Wuthrich, K. NMR solution structure of the human prion protein. Proc. Natl. Acad. Sci. USA 2000, 97, 145–150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Fisher, J.C.; Mathew, R.; Ou, L.; Otieno, S.; Sublet, J.; Xiao, L.; Chen, J.; Roussel, M.F.; Kriwacki, R.W. Intrinsic disorder mediates the diverse regulatory functions of the Cdk inhibitor p21. Nat. Chem. Biol. 2011, 7, 214–221. [Google Scholar] [CrossRef] [Green Version]
- Wong, L.E.; Kim, T.H.; Muhandiram, D.R.; Forman-Kay, J.D.; Kay, L.E. NMR Experiments for Studies of Dilute and Condensed Protein Phases: Application to the Phase-Separating Protein CAPRIN1. J. Am. Chem. Soc. 2020, 142, 2471–2489. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, J.; Mok, K.; Lee, J.; Han, K.H. Salient Features of Monomeric Alpha-Synuclein Revealed by NMR Spectroscopy. Biomolecules 2020, 10, 428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kosol, S.; Contreras-Martos, S.; Cedeño, C.; Tompa, P. Structural Characterization of Intrinsically Disordered Proteins by NMR Spectroscopy. Molecules 2013, 18, 10802–10828. [Google Scholar] [CrossRef] [Green Version]
- Dyson, H.J.; Wright, P.E. NMR illuminates intrinsic disorder. Curr. Opin. Struct. Biol. 2021, 70, 44–52. [Google Scholar] [CrossRef]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Shan, Y.; et al. Atomic-Level Characterization of the Structural Dynamics of Proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef] [Green Version]
- Lindorff-Larsen, K.; Trbovic, N.; Maragakis, P.; Piana, S.; Shaw, D.E. Structure and Dynamics of an Unfolded Protein Examined by Molecular Dynamics Simulation. J. Am. Chem. Soc. 2012, 134, 3787–3791. [Google Scholar] [CrossRef]
- Ahmed, M.C.; Skaanning, L.K.; Jussupow, A.; Newcombe, E.A.; Kragelund, B.B.; Camilloni, C.; Langkilde, A.E.; Lindorff-Larsen, K. Refinement of α-Synuclein Ensembles Against SAXS Data: Comparison of Force Fields and Methods. Front. Mol. Biosci. 2021, 8, 216. [Google Scholar] [CrossRef]
- Wilson, C.J.; Chang, M.; Karttunen, M.; Choy, W.Y. KEAP1 Cancer Mutants: A Large-Scale Molecular Dynamics Study of Protein Stability. Int. J. Mol. Sci. 2021, 22, 5408. [Google Scholar] [CrossRef] [PubMed]
- Rauscher, S.; Gapsys, V.; Gajda, M.J.; Zweckstetter, M.; de Groot, B.L.; Grubmüller, H. Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cino, E.A.; Choy, W.Y.; Karttunen, M. Characterization of the Free State Ensemble of the CoRNR Box Motif by Molecular Dynamics Simulations. J. Phys. Chem. B 2016, 120, 1060–1068. [Google Scholar] [CrossRef] [PubMed]
- Samantray, S.; Yin, F.; Kav, B.; Strodel, B. Different Force Fields Give Rise to Different Amyloid Aggregation Pathways in Molecular Dynamics Simulations. J. Chem. Inf. Model. 2020, 60, 6462–6475. [Google Scholar] [CrossRef]
- Nasica-Labouze, J.; Nguyen, P.H.; Sterpone, F.; Berthoumieu, O.; Buchete, N.V.; Coté, S.; Simone, A.D.; Doig, A.J.; Faller, P.; Garcia, A.; et al. Amyloid β Protein and Alzheimer’s Disease: When Computer Simulations Complement Experimental Studies. Chem. Rev. 2015, 115, 3518–3563. [Google Scholar] [CrossRef]
- Piana, S.; Lindorff-Larsen, K.; Shaw, D.E. Atomic-level description of ubiquitin folding. Proc. Natl. Acad. Sci. USA 2013, 110, 5915–5920. [Google Scholar] [CrossRef] [Green Version]
- Dror, R.O.; Dirks, R.M.; Grossman, J.; Xu, H.; Shaw, D.E. Biomolecular Simulation: A Computational Microscope for Molecular Biology. Annu. Rev. Biophys. 2012, 41, 429–452. [Google Scholar] [CrossRef] [Green Version]
- Best, R.B.; Hummer, G.; Eaton, W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17874–17879. [Google Scholar] [CrossRef] [Green Version]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, C.J.; Choy, W.-Y.; Karttunen, M. AlphaFold2: A Role for Disordered Protein/Region Prediction? Int. J. Mol. Sci. 2022, 23, 4591. https://doi.org/10.3390/ijms23094591
Wilson CJ, Choy W-Y, Karttunen M. AlphaFold2: A Role for Disordered Protein/Region Prediction? International Journal of Molecular Sciences. 2022; 23(9):4591. https://doi.org/10.3390/ijms23094591
Chicago/Turabian StyleWilson, Carter J., Wing-Yiu Choy, and Mikko Karttunen. 2022. "AlphaFold2: A Role for Disordered Protein/Region Prediction?" International Journal of Molecular Sciences 23, no. 9: 4591. https://doi.org/10.3390/ijms23094591
APA StyleWilson, C. J., Choy, W. -Y., & Karttunen, M. (2022). AlphaFold2: A Role for Disordered Protein/Region Prediction? International Journal of Molecular Sciences, 23(9), 4591. https://doi.org/10.3390/ijms23094591