The Dynamics of Calcium Signaling in Beta Cells—A Discussion on the Comparison of Experimental and Modelling Data
Abstract
:1. Introduction
1.1. Physiological Background
1.2. Methods for the Determination of the Plasma Membrane Potential
1.3. Methods to Study the Cytosolic Calcium Concentration
1.4. Evolution of Models
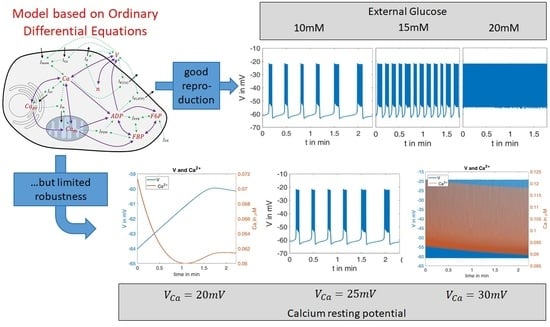
2. Results and Discussion
2.1. Modeling of Membrane Currents
2.2. Inflence of Agents
2.2.1. Variation of Glucose Concentration
- The quantitative values of the membrane potential (except for the small deviations in the maximum potential during the bursts).
- The characteristics of the curves (alternation between high-frequency and low-frequency fractions).
- The length and variability of the phases between the action potentials. In particular, the ability to reproduce this variability with a set of deterministic ordinary differential equations is very remarkable.
- The number of action potentials in the considered time interval.
- the duration of the action potentials is of a comparable size.
- the number of spikes in relation to the duration matches very well.
- The distance between the spikes within the action potential increases over time. This is a well-known feature, see, e.g., [41].
- In the simulation as well as in the measurement, the time between two bursts of action potentials shortens with increasing (increasing glucose supply).
- At or , respectively, there are practically no more resting phases; action potentials are permanently present.
- In the experimental registrations, the peak value of the action potentials decreases with increasing and time; in the simulation, this value remains nearly constant (at about ).
2.2.2. Variation of K+ Concentration
2.2.3. Effects of Pharmacological Block of KATP Channels by Tolbutamide
2.3. Influence of the Measurement Itself
3. Materials and Methods
3.1. Chemicals
3.2. Tissue and Tissue Culture
3.3. Measurement of the Plasma Membrane Potential
3.4. Microfluorimetric Measurement of the Cytosolic Ca2+ Concentration
3.5. Modelling
- How robust is the model when tested considering novel experimental results?
- How good is the response of the model to pharmacological agents?
- Is the model helpful to understand the influence of the measuring technique?
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Simplified Electrical Model for the Cell Membrane

Appendix B. Governing Equations and Parameters
| (A2) | |
| (A3) | |
| (A4) | |
| (A5) | |
| (A6) | |
| (A7) | |
| (A8) | |
| (A9) |
| Measure and Formula | Meaning |
|---|---|
| Current due to Calcium ion influx | |
| Current due to Potassium ion efflux | |
| Current due to Calcium-dependent potassium ion efflux | |
| Current due to ATP-dependent potassium ion efflux | |
| Steady-state potassium ion activity | |
| Calcium influx into the cell | |
| Calcium influx into the ER | |
| Calcium influx into the mitochondria | |
| PFK activity according to [33] | |
| Weight factor according to [33] | |
| Amount of adenosine monophosphate | |
| Pyravate dehydrogenase reaction rate | |
| Feedback on pyravate dehydrogenase by calcium in the mitochondria | |
| Amount of ATP |
| (else) | ||
References
- Coore, H.G.; Randle, P.J. Regulation of insulin secretion studied with pieces of rabbit pancreas incubated in vitro. Biochem. J. 1964, 93, 66. [Google Scholar] [CrossRef]
- Malaisse, W.J. Insulin release: The fuel concept. Diabète Métabolisme 1983, 9, 313–320. [Google Scholar]
- Cook, D.L.; Hales, N. Intracellular ATP directly blocks K+ channels in pancreatic B-cells. Nature 1984, 311, 271–273. [Google Scholar] [CrossRef] [PubMed]
- Inagaki, N.; Gonoi, T.; Clement IV, J.P.; Namba, N.; Inazawa, J.; Gonzalez, G.; Aguilar-Bryan, L.; Seino, S.; Bryan, J. Reconstitution of I KATP: An inward rectifier subunit plus the sulfonylurea receptor. Science 1995, 270, 1166–1170. [Google Scholar] [CrossRef]
- Bergsten, P.; Grapengiesser, E.; Gylfe, E.; Tengholm, A.; Hellman, B. Synchronous oscillations of cytoplasmic Ca2+ and insulin release in glucose-stimulated pancreatic islets. J. Biol. Chem. 1994, 269, 8749–8753. [Google Scholar] [CrossRef]
- Henquin, J.-C. Triggering and amplifying pathways of regulation of insulin secretion by glucose. Diabetes 2000, 49, 1751–1760. [Google Scholar] [CrossRef] [PubMed]
- Rustenbeck, I.; Schulze, T.; Morsi, M.; Alshafei, M.; Panten, U. What is the metabolic amplification of insulin secretion and is it (still) relevant? Metabolites 2021, 11, 355. [Google Scholar] [CrossRef] [PubMed]
- Gaus, B.; Brüning, D.; Groß, S.; Müller, M.; Rustenbeck, I. The changing view of insulin granule mobility: From conveyor belt to signaling hub. Front. Endocrinol. 2022, 13, 983152. [Google Scholar] [CrossRef]
- Georgiadou, E.; Rutter, G.A. Control by Ca2+ of mitochondrial structure and function in pancreatic β-cells. Cell Calcium 2020, 91, 102282. [Google Scholar] [CrossRef]
- Hughes, E.; Lee, A.K.; Tse, A. Dominant role of sarcoendoplasmic reticulum Ca2+-ATPase pump in Ca2+ homeostasis and exocytosis in rat pancreatic β-cells. Endocrinology 2006, 147, 1396–1407. [Google Scholar] [CrossRef]
- Houamed, K.M.; Sweet, I.R.; Satin, L.S. BK channels mediate a novel ionic mechanism that regulates glucose-dependent electrical activity and insulin secretion in mouse pancreatic β-cells. J. Physiol. 2010, 588, 3511–3523. [Google Scholar] [CrossRef]
- Plášek, J.; Sigler, K. Slow fluorescent indicators of membrane potential: A survey of different approaches to probe response analysis. J. Photochem. Photobiol. B Biol. 1996, 33, 101–124. [Google Scholar] [CrossRef] [PubMed]
- Molleman, A. Patch Clamping: An Introductory Guide to Patch Clamp Electrophysiology; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 0470856513. [Google Scholar]
- Dean, P.M.; Matthews, E.K. Glucose-induced electrical activity in pancreatic islet cells. J. Physiol. 1970, 210, 255–264. [Google Scholar] [CrossRef] [PubMed]
- Henquin, J.-C.; Meissner, H.P.; Schmeer, W. Cyclic variations of glucose-induced electrical activity in pancreatic B cells. Pflüg. Arch. 1982, 393, 322–327. [Google Scholar] [CrossRef] [PubMed]
- Neher, E.; Sakmann, B. Single-channel currents recorded from membrane of denervated frog muscle fibres. Nature 1976, 260, 799–802. [Google Scholar] [CrossRef]
- Hamill, O.P.; Marty, A.; Neher, E.; Sakmann, B.; Sigworth, F.J. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflüg. Arch. 1981, 391, 85–100. [Google Scholar] [CrossRef]
- Horn, R.; Marty, A. Muscarinic activation of ionic currents measured by a new whole-cell recording method. J. Gen. Physiol. 1988, 92, 145–159. [Google Scholar] [CrossRef]
- Tsien, R.Y.; Rink, T.J. Neutral carrier ion-selective microelectrodes for measurement of intracellular free calcium. Biochim. Biophys. Acta (BBA)-Biomembr. 1980, 599, 623–638. [Google Scholar] [CrossRef]
- Grynkiewicz, G.; Poenie, M.; Tsien, R.Y. A new generation of Ca2+ indicators with greatly improved fluorescence properties. J. Biol. Chem. 1985, 260, 3440–3450. [Google Scholar] [CrossRef]
- McCombs, J.E.; Palmer, A.E. Measuring calcium dynamics in living cells with genetically encodable calcium indicators. Methods 2008, 46, 152–159. [Google Scholar] [CrossRef]
- Minta, A.; Kao, J.P.Y.; Tsien, R.Y. Fluorescent indicators for cytosolic calcium based on rhodamine and fluorescein chromophores. J. Biol. Chem. 1989, 264, 8171–8178. [Google Scholar] [CrossRef]
- Thomas, D.; Tovey, S.C.; Collins, T.J.; Bootman, M.D.; Berridge, M.J.; Lipp, P. A comparison of fluorescent Ca2+ indicator properties and their use in measuring elementary and global Ca2+ signals. Cell Calcium 2000, 28, 213–223. [Google Scholar] [CrossRef] [PubMed]
- Chay, T.R.; Keizer, J. Minimal model for membrane oscillations in the pancreatic beta-cell. Biophys. J. 1983, 42, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-J.; Tengholm, A.; Grapengiesser, E.; Hellman, B.; Gylfe, E. Origin of slow and fast oscillations of Ca2+ in mouse pancreatic islets. J. Physiol. 1998, 508, 471–481. [Google Scholar] [CrossRef]
- Rorsman, P.; Eliasson, L.; Kanno, T.; Zhang, Q.; Gopel, S. Electrophysiology of pancreatic β-cells in intact mouse islets of Langerhans. Prog. Biophys. Mol. Biol. 2011, 107, 224–235. [Google Scholar] [CrossRef]
- Kjems, L.L.; Ravier, M.A.; Jonas, J.-C.; Henquin, J.-C. Do oscillations of insulin secretion occur in the absence of cytoplasmic Ca2+ oscillations in β-cells? Diabetes 2002, 51, S177–S182. [Google Scholar] [CrossRef]
- Satin, L.S.; Butler, P.C.; Ha, J.; Sherman, A.S. Pulsatile insulin secretion, impaired glucose tolerance and type 2 diabetes. Mol. Asp. Med. 2015, 42, 61–77. [Google Scholar] [CrossRef]
- Zmazek, J.; Klemen, M.S.; Markovič, R.; Dolenšek, J.; Marhl, M.; Stožer, A.; Gosak, M. Assessing different temporal scales of calcium dynamics in networks of beta cell populations. Front. Physiol. 2021, 12, 612233. [Google Scholar] [CrossRef]
- Bertram, R.; Previte, J.; Sherman, A.; Kinard, T.A.; Satin, L.S. The phantom burster model for pancreatic β-cells. Biophys. J. 2000, 79, 2880–2892. [Google Scholar] [CrossRef] [PubMed]
- Bertram, R.; Sherman, A. Filtering of calcium transients by the endoplasmic reticulum in pancreatic β-cells. Biophys. J. 2004, 87, 3775–3785. [Google Scholar] [CrossRef] [PubMed]
- Bertram, R.; Sherman, A.; Satin, L.S. Metabolic and electrical oscillations: Partners in controlling pulsatile insulin secretion. Am. J. Physiol. -Endocrinol. Metab. 2007, 293, E890–E900. [Google Scholar] [CrossRef]
- Smolen, P. A model for glycolytic oscillations based on skeletal muscle phosphofructokinase kinetics. J. Theor. Biol. 1995, 174, 137–148. [Google Scholar] [CrossRef]
- McKenna, J.P.; Ha, J.; Merrins, M.J.; Satin, L.S.; Sherman, A.; Bertram, R. Ca2+ effects on ATP production and consumption have regulatory roles on oscillatory islet activity. Biophys. J. 2016, 110, 733–742. [Google Scholar] [CrossRef] [PubMed]
- Merrins, M.J.; van Dyke, A.R.; Mapp, A.K.; Rizzo, M.A.; Satin, L.S. Direct Measurements of Oscillatory Glycolysis in Pancreatic Islet β-Cells Using Novel Fluorescence Resonance Energy Transfer (FRET) Biosensors for Pyruvate Kinase M2 Activity. J. Biol. Chem. 2013, 288, 33312–33322. [Google Scholar] [CrossRef]
- Marinelli, I.; Vo, T.; Gerardo-Giorda, L.; Bertram, R. Transitions between bursting modes in the integrated oscillator model for pancreatic β-cells. J. Theor. Biol. 2018, 454, 310–319. [Google Scholar] [CrossRef] [PubMed]
- McKenna, J.P.; Bertram, R. Fast-slow analysis of the Integrated Oscillator Model for pancreatic β-cells. J. Theor. Biol. 2018, 457, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Braun, M.; Ramracheya, R.; Bengtsson, M.; Zhang, Q.; Karanauskaite, J.; Partridge, C.; Johnson, P.R.; Rorsman, P. Voltage-gated ion channels in human pancreatic β-cells: Electrophysiological characterization and role in insulin secretion. Diabetes 2008, 57, 1618–1628. [Google Scholar] [CrossRef]
- Gilon, P.; Chae, H.-Y.; Rutter, G.A.; Ravier, M.A. Calcium signaling in pancreatic β-cells in health and in Type 2 diabetes. Cell Calcium 2014, 56, 340–361. [Google Scholar] [CrossRef]
- Marinelli, I.; Thompson, B.M.; Parekh, V.S.; Fletcher, P.A.; Gerardo-Giorda, L.; Sherman, A.S.; Satin, L.S.; Bertram, R. Oscillations in K (ATP) conductance drive slow calcium oscillations in pancreatic β-cells. Biophys. J. 2022, 121, 1449–1464. [Google Scholar] [CrossRef]
- Sanchez-Andres, J.V.; Gomis, A.; Valdeolmillos, M. The electrical activity of mouse pancreatic beta-cells recorded in vivo shows glucose-dependent oscillations. J. Physiol. 1995, 486, 223–228. [Google Scholar] [CrossRef]
- Detimary, P.; Jonas, J.-C.; Henquin, J.-C. Possible links between glucose-induced changes in the energy state of pancreatic B cells and insulin release. Unmasking by decreasing a stable pool of adenine nucleotides in mouse islets. J. Clin. Investig. 1995, 96, 1738–1745. [Google Scholar] [CrossRef] [PubMed]
- Brüning, D.; Morsi, M.; Früh, E.; Scherneck, S.; Rustenbeck, I. Metabolic Regulation of Hormone Secretion in Beta-Cells and Alpha-Cells of Female Mice: Fundamental Differences. Endocrinology 2022, 163, bqac125. [Google Scholar] [CrossRef]
- Rorsman, P.; Trube, G. Calcium and delayed potassium currents in mouse pancreatic beta-cells under voltage-clamp conditions. J. Physiol. 1986, 374, 531–550. [Google Scholar] [CrossRef] [PubMed]
- Hatlapatka, K.; Willenborg, M.; Rustenbeck, I. Plasma membrane depolarization as a determinant of the first phase of insulin secretion. Am. J. Physiol.-Endocrinol. Metab. 2009, 297, E315–E322. [Google Scholar] [CrossRef]
- Willenborg, M.; Hatlapatka, K.; Ghaly, H.; Belz, M.; Panten, U.; Rustenbeck, I. Studies of first phase insulin secretion using imposed plasma membrane depolarization. Front. Biosci.-Sch. 2011, 3, 662–679. [Google Scholar]
- Belz, M.; Willenborg, M.; Görgler, N.; Hamada, A.; Schumacher, K.; Rustenbeck, I. Insulinotropic effect of high potassium concentration beyond plasma membrane depolarization. Am. J. Physiol.-Endocrinol. Metab. 2014, 306, E697–E706. [Google Scholar] [CrossRef] [PubMed]
- Babenko, A.P.; Gonzalez, G.; Bryan, J. The tolbutamide site of SUR1 and a mechanism for its functional coupling to KATP channel closure. FEBS Lett. 1999, 459, 367–376. [Google Scholar] [CrossRef]
- Gold, R.S. The Axon Guide for Electrophysiology and Biophysics, Labaratory Techniques; Comp. Axon Instruments; Molecular Devices: Sunnyvale, CA, USA, 1993. [Google Scholar]
- Klec, C.; Madreiter-Sokolowski, C.T.; Stryeck, S.; Sachdev, V.; Duta-Mare, M.; Gottschalk, B.; Depaoli, M.R.; Rost, R.; Hay, J.; Waldeck-Weiermair, M. Glycogen synthase kinase 3 beta controls Presenilin-1-mediated endoplasmic reticulum Ca2+ leak directed to mitochondria in pancreatic islets and β-cells. Cell. Physiol. Biochem. Int. J. Exp. Cell. Physiol. Biochem. Pharmacol. 2019, 52, 57. [Google Scholar]
- Klec, C.; Madreiter-Sokolowski, C.T.; Ziomek, G.; Stryeck, S.; Sachdev, V.; Duta-Mare, M.; Gottschalk, B.; Depaoli, M.R.; Rost, R.; Hay, J. Presenilin-1 established ER-Ca2+ leak: A follow up on its importance for the initial insulin secretion in pancreatic islets and beta-cells upon elevated glucose. Cell. Physiol. Biochem. 2019, 53, 573–586. [Google Scholar]
- Müller, M.; Glombek, M.; Powitz, J.; Brüning, D.; Rustenbeck, I. A Cellular Automaton Model as a First Model-Based Assessment of Interacting Mechanisms for Insulin Granule Transport in Beta Cells. Cells 2020, 9, 1487. [Google Scholar] [CrossRef]
- Parekh, A.B. Ca2+ microdomains near plasma membrane Ca2+ channels: Impact on cell function. J. Physiol. 2008, 586, 3043–3054. [Google Scholar] [CrossRef] [PubMed]
- Hoppa, M.B.; Collins, S.; Ramracheya, R.; Hodson, L.; Amisten, S.; Zhang, Q.; Johnson, P.; Ashcroft, F.M.; Rorsman, P. Chronic palmitate exposure inhibits insulin secretion by dissociation of Ca2+ channels from secretory granules. Cell Metab. 2009, 10, 455–465. [Google Scholar] [CrossRef] [PubMed]
- Félix-Martínez, G.J.; Godínez-Fernández, J.R. Modeling the spatiotemporal distribution of Ca2+ during action potential firing in human pancreatic β-cells. Biomed. Phys. Eng. Express 2017, 3, 25020. [Google Scholar] [CrossRef]
- Félix-Martínez, G.J.; Godínez-Fernández, J.R. Effect of cell size on insulin secretion in human β-cells: A simulation study. Health Technol. 2020, 10, 379–383. [Google Scholar] [CrossRef]
- Johnston, D.; Wu, S.M.-S. Foundations of Cellular Neurophysiology; MIT Press: Cambridge, MA, USA, 1994; ISBN 0262293498. [Google Scholar]


















| K30 | 0.30 | 0.12 | 0.18 | 1 |
| K20 | 0.22 | 0.09 | 0.13 | 1.38 |
| K15 | 0.14 | 0.08 | 0.06 | 3.0 |
| Measurement | |||||
|---|---|---|---|---|---|
| K30 | 0.50 | 1 | 0.46 | 1 | 1 |
| K20 | 0.46 | 1.09 | 0.33 | 1.39 | 1.38 |
| K15 | 0.43 | 1.16 | 0.13 | 3.54 | 3.0 |
| State Variable | Meaning |
|---|---|
| Membrane potential | |
| Potassium ion activity | |
| Calcium ion concentration in the cytosol | |
| Calcium ion concentration in the mitochondria | |
| Calcium ion concentration in the endoplasmic reticulum | |
| Amount of fructose-6-phosphate | |
| Amount of fructose-6-biphosphate | |
| Amount of ADP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müller, M.; Walkling, J.; Seemann, N.; Rustenbeck, I. The Dynamics of Calcium Signaling in Beta Cells—A Discussion on the Comparison of Experimental and Modelling Data. Int. J. Mol. Sci. 2023, 24, 3206. https://doi.org/10.3390/ijms24043206
Müller M, Walkling J, Seemann N, Rustenbeck I. The Dynamics of Calcium Signaling in Beta Cells—A Discussion on the Comparison of Experimental and Modelling Data. International Journal of Molecular Sciences. 2023; 24(4):3206. https://doi.org/10.3390/ijms24043206
Chicago/Turabian StyleMüller, Michael, Jonas Walkling, Nele Seemann, and Ingo Rustenbeck. 2023. "The Dynamics of Calcium Signaling in Beta Cells—A Discussion on the Comparison of Experimental and Modelling Data" International Journal of Molecular Sciences 24, no. 4: 3206. https://doi.org/10.3390/ijms24043206
APA StyleMüller, M., Walkling, J., Seemann, N., & Rustenbeck, I. (2023). The Dynamics of Calcium Signaling in Beta Cells—A Discussion on the Comparison of Experimental and Modelling Data. International Journal of Molecular Sciences, 24(4), 3206. https://doi.org/10.3390/ijms24043206