Theoretically Revealing the Response of Intermolecular Vibration Energy Transfer and Decomposition Process of the DNTF System to Electric Fields Using Two-Dimensional Infrared Spectra
Abstract
:1. Introduction
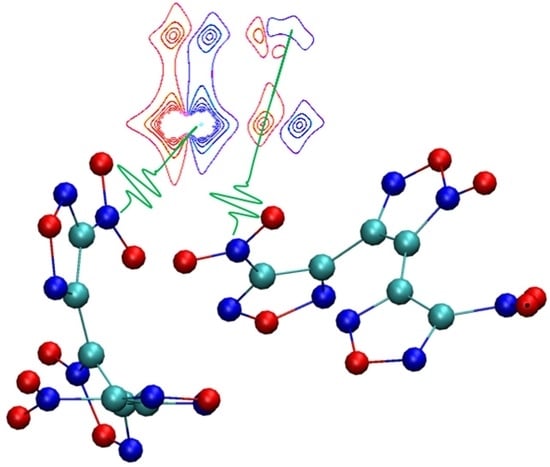
2. Results and Discussion
3. Methods and Materials
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chung, K.; Rozumov, E.; Kaminsky, D.; Anderson, P.; Cook, P.; Sawka, W.; McPherson, M.; Buescher, T. Development of Electrically controlled energetic materials. ESC Trans. 2013, 50, 59–66. [Google Scholar] [CrossRef]
- Tasker, D.G.; Whitley, V.H.; Mace, J.L.; Pemberton, S.J.; Lee, R.J. Electromagnetic effects on explosive reaction and plasma. In Proceedings of the 14th International Detonation Symposium, Coeur d’Alene, Idaho, 11–16 April 2010. [Google Scholar]
- Lee, R.J.; Forbes, J.W.; Tasker, D.G.; Orme, R.S. Changes in Blow-off-velocity observed in two explosives at the threshold for sustained ignition using the modified gap test. In Shock Compression of Condensed Matter 2009, Proceedings of the American Physical Society Topical Group on Shock Compression of Condensed Matter, Nashville, TN, USA, 28 June–3 July 2009; Furnish, M.D., Ed.; American Institute of Physics: Melville, NY, USA, 2009. [Google Scholar]
- Lee, R.J.; Forbes, J.W.; Palermo, E.; Wilson, W.H. Effects of electric fields on sensitivity of an HMX based explosive. In Shock Compression of Condensed Matter 2007, Proceedings of the Conference of the American Physical Society, Waikoloa, HI, USA, 24–29 June 2007; American Institute of Physics: Melville, NY, USA, 2007; pp. 963–966. [Google Scholar]
- Politzer, P.; Murray, J.S.; Lane, P. Computational determination of effects of electric fields upon “trigger linkages” of prototypical energetic molecules. Int. J. Quantum Chem. 2009, 109, 534–539. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Computed effects of electric fields upon the C-NO2 and N-NO2 bonds of nitromethane and dimethylnitramine. Int. J. Quantum Chem. 2009, 109, 3–7. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Concha, M.C.; Lane, P. Effects of Electric Fields Upon Energetic Molecules: Nitromethane and Dimethylnitramine. Cent. Eur. J. Energet. Mater. 2007, 4, 3–21. [Google Scholar]
- Ren, F.D.; Cao, D.L.; Shi, W.J.; You, M. A dynamic prediction of stability for nitromethane in external electric field. RSC Adv. 2017, 7, 47063–47072. [Google Scholar] [CrossRef] [Green Version]
- Ren, F.D.; Cao, D.L.; Shi, W.J. A dynamics prediction of nitromethane → methyl nitrite isomerization in external electric field. J. Mol. Model. 2016, 22, 96. [Google Scholar] [CrossRef]
- Ren, F.D.; Cao, D.L.; Shi, W.J.; You, M.; Li, M. A theoretical prediction of the possible trigger linkage of CH3NO2 and NH2NO2 in an external electric field. J. Mol. Model. 2015, 21, 145. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y.; Yu, T.; Lai, W.; Guo, W.; Ge, Z.; Ma, Z. Structural Rearrangement of Energetic Materials under an External Electric Field: A Case Study of Nitromethane. J. Phys. Chem. A 2018, 122, 2129–2134. [Google Scholar] [CrossRef]
- Wood, M.A.; Van Duin, A.C.; Strachan, A. Coupled thermal and electromagnetic induced decomposition in the molecular explosive αHMX; a reactive molecular dynamics study. J. Phys. Chem. A 2014, 118, 885–895. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Z.; Li, J.; Guan, X.; Huang, X.; Zhou, C. Crystal Structure of 3,4-dinitrofurazanofuroxan. Chin. J. Explos. Propell. 2005, 28, 43–52. [Google Scholar]
- Sheremerev, A.V.; Ivanova, E.A.; Spiridonova, N.P.; Melnikova, S.F.; Antipin, M.Y. Desilylative nitration of C,N-disilylated 3-amino-4-methylfurazan. J. Heterocycl. Chem. 2005, 42, 1237. [Google Scholar] [CrossRef]
- Nan, H.; Pan, Q.; Jiang, F.; Wang, X.; Jin, P.; Zhang, K. In situ infrared thermal decomposition kinetics and mechanism of DNTF. Chin. J. Energet. Mater. 2022, 30, 604–610. [Google Scholar]
- Ren, X.; Liu, Z.; Wang, X.; Zhao, X.F.; Xie, M.; Heng, S. Investigated on the flash thermolysis of 3, 4-dinitrofuruzan-furoxan by T-jump/FTIR Spectroscopy. Acta Phys.-Chim. Sin. 2010, 26, 547–551. [Google Scholar]
- Ma, H.-X.; Song, J.-R.; Xiao, H.-M.; Hu, R.-Z.; Zhao, F.-Q. Density Functional Theoretical Investigation on 3, 4-Dinitrofurazanfuroxan (DNTF). Chin. J. Explos. Propell. 2006, 3, 43. [Google Scholar]
- Li, Y.; Yuan, J.; Zhao, W.; Qu, Y.; Xing, X.; Meng, J.; Liu, Y. Application and Development of 3, 4-Bis (3-nitrofurazan-4-yl) furoxan (DNTF). Russ. J. Gen. Chem. 2021, 91, 445–455. [Google Scholar] [CrossRef]
- Nan, H.; Jia, X.; Wang, X.; Liu, H.; Jiang, F.; Zhang, P. Mechanical and Electronic Properties of DNTF Crystals under Different Pressure. Crystals 2021, 11, 1180. [Google Scholar] [CrossRef]
- Zhang, G.; Jin, S.; Li, L.; Li, Y.; Li, Z.; Wang, D.; Zhang, B.; Jing, B.; Shu, Q. Thermal stability assessment of 3, 4-bis (3-nitrofurazan-4-yl) furoxan (DNTF) by accelerating rate calorimeter. J. Therm. Anal. Calorim. 2016, 126, 1185–1190. [Google Scholar] [CrossRef]
- Cole-Filipiak, N.C.; Marquez, M.; Knepper, R.; Harmon, R.; Wiese-Smith, D.; Schrader, P.; Wood, M.; Ramasesha, K. Ultrafast spectroscopic studies of vibrational energy transfer in energetic materials. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2020; Volume 2272, p. 060006. [Google Scholar]
- Cole-Filipiak, N.C.; Knepper, R.; Wood, M.; Ramasesha, K. Sub-picosecond to Sub-nanosecond Vibrational Energy Transfer Dynamics in Pentaerythritol Tetranitrate. J. Phys. Chem. Lett. 2020, 11, 6664–6669. [Google Scholar] [CrossRef]
- Ostrande, J.S.; Knepper, R.; Tappan, A.S.; Kay, J.J.; Zanni, M.T.; Farrow, D.A. Energy Transfer Between Coherently Delocalized States in Thin Films of the Explosive Pentaerythritol Tetranitrate (PETN) Revealed by Two-Dimensional Infrared Spectroscopy. J. Phys. Chem. B 2017, 121, 1352–1361. [Google Scholar] [CrossRef]
- Shi, L.; Yu, P.; Zhao, J.; Wang, J. Ultrafast Intermolecular Vibrational Energy Transfer in Hexahydro-1,3,5-Trinitro-1,3,5-Triazine in Molecular Crystal by 2D IR Spectroscopy. J. Phys. Chem. C 2020, 124, 2388–2398. [Google Scholar] [CrossRef]
- Ren, H.C.; Ji, L.X.; Jia, X.Z.; Liu, R.P.; Zhang, X.Q.; Wei, D.Q.; Wang, X.F.; Ji, G.F. Intermolecular vibration energy transfer process in two CL-20-based cocrystals theoretically revealed by two-dimensional infrared spectra. Molecules 2022, 27, 2153. [Google Scholar] [CrossRef]
- Bernstein, J. Ab initio study of energy transfer rates and impact sensitivities of crystalline explosives. J. Chem. Phys. 2018, 148, 084502. [Google Scholar] [CrossRef]
- Ramasesha, K.; Wood, M.; Cole-Filipiak, N.C.; Knepper, R. Experimental and Theoretical Studies of Ultrafast Vibrational Energy Transfer Dynamics in Energetic Materials; Sandia National Lab: Livermorel, CA, USA, 2020. [Google Scholar]
- Joshi, K.; Losada, M.; Chaudhuri, S. Intermolecular energy transfer dynamics at a hot-spot interface in RDX crystals. J. Phys. Chem. A 2016, 120, 477–489. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Bond order analysis based on the Laplacian of electron density in Fuzzy overlap space. J. Phys. Chem. A 2013, 117, 3100–3108. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Independent gradient model based on Hirshfeld partition: A new method for visual study of interactions in chemical system. J. Comput. Chem. 2022, 43, 539–555. [Google Scholar] [CrossRef]
- Hamm, P.; Zanni, M.T. Concepts and Methods of 2D Infrared Spectroscopy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Kraack, J.P. Ultrafast Structural Molecular Dynamics Investigated with 2D Infrared Spectroscopy Methods. In Multidimensional Time-Resolved Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2019; pp. 113–205. [Google Scholar]
- Becke, A.D. Density-Functional Exchange Approximation with Correct Asymptotic Behavior. Phys. Rev. A. 1988, 38, 3098. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuserria, G.E.; Robb, M.A.; Cheeseman, J.R.; Schlmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision A. 03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-salvetti Correlation-energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Jamróz, M.H. Vibrational Energy Distribution Analysis (VEDA): Scopes and limitations. Spectrochim. Acta A 2013, 114, 220–230. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A Thorough Benchmark of Density Functional Methods for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef]
- He, P.; Zhang, J.-G.; Wang, K.; Yin, X.; Jin, X.; Zhang, T.-L. Extensive theoretical studies on two new members of the FOX-7 family: 5-(dinitromethylene)-1,4-dinitramino-tetrazole and 1,1′-dinitro-4,4′-diamino-5,5′-bitetrazole as energetic compounds. Phys. Chem. Chem. Phys. 2015, 17, 5840–5848. [Google Scholar] [CrossRef]
- Zhai, D.; Wang, J.; Hao, L.; Ma, C.; Ma, P.; Pan, Y.; Jiang, J. Molecular design and properties of bridged energetic pyridines derivatives. RSC Adv. 2019, 9, 37747–37758. [Google Scholar] [CrossRef] [Green Version]
- Stobiecka, A.; Sikora, M.; Bonikowski, R.; Kula, J. An exploratory study on the peroxyl-radical-scavenging activity of 2,6-dimethyl-5-hepten-2-ol and its heterocyclic analogues. J. Mol. Struct. 2016, 1107, 82–90. [Google Scholar] [CrossRef]
- Zhang, Y.; Suo, B.; Wang, Z.; Zhang, N.; Li, Z.; Lei, Y.; Zou, W.; Gao, J.; Peng, D.; Pu, Z.; et al. BDF: A relativistic electronic structure program package. J. Chem. Phys. 2020, 152, 064113. [Google Scholar] [CrossRef]
- Fast, P.L.; Corchado, J.; Sanchez, M.L.; Truhlar, D.G. Optimized Parameters for Scaling Correlation Energy. J. Phys. Chem. A 1999, 103, 3139–3143. [Google Scholar] [CrossRef]
- Grimme, S. Density Functional Theory with London Dispersion Corrections. Wiley Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Mewes, J.; Ehlert, S.; Grimme, S. Extension and evaluation of the D4 London-dispersion model for periodic systems. Phys. Chem. Chem. Phys. 2020, 22, 8499–8512. [Google Scholar] [CrossRef]
- Caldweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Soicher, S.; Spicher, S.; Bannwarth, C.; Grimme, S. A generally applicable atomic-charge dependent London dispersion correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef]
- Kesharwani, M.K.; Brauer, B.; Martin, J.M.L. Frequency and Zero-Point Vibrational Energy Scale Factors for Double-Hybrid Densith Functionals (and Other Selected Methods): Can Anharmonic Force Fields Be Avoided? J. Phys. Chem. A 2015, 119, 1701–1714. [Google Scholar] [CrossRef]








| Bond | DNTFI | DNTFII | DNTFIII | DNTFIV | Experiment |
|---|---|---|---|---|---|
| N7-O6 | 1.213 | 1.211 | 1.218 | 1.211 | 1.207 |
| N7-O5 | 1.217 | 1.221 | 1.218 | 1.221 | 1.217 |
| C1-N7 | 1.467 | 1.464 | 1.459 | 1.464 | 1.459 |
| C1-C2 | 1.433 | 1.429 | 1.426 | 1.429 | 1.421 |
| C1-N1 | 1.294 | 1.297 | 1.300 | 1.297 | 1.289 |
| N1-O1 | 1.360 | 1.357 | 1.350 | 1.356 | 1.372 |
| N2-O1 | 1.364 | 1.367 | 1.367 | 1.368 | 1.375 |
| N2-C2 | 1.311 | 1.311 | 1.308 | 1.311 | 1.303 |
| C2-C3 | 1.441 | 1.441 | 1.444 | 1.442 | 1.445 |
| C3-N3 | 1.337 | 1.337 | 1.329 | 1.336 | 1.336 |
| N3-O4 | 1.201 | 1.198 | 1.207 | 1.201 | 1.212 |
| C3-C4 | 1.428 | 1.424 | 1.422 | 1.421 | 1.405 |
| N8-O7 | 1.234 | 1.216 | 1.224 | 1.224 | 1.255 |
| N8-O8 | 1.204 | 1.220 | 1.210 | 1.211 | 1.227 |
| C6-N8 | 1.454 | 1.447 | 1.463 | 1.461 | 1.442 |
| C5-C6 | 1.426 | 1.424 | 1.425 | 1.424 | 1.415 |
| C6-N6 | 1.297 | 1.295 | 1.297 | 1.297 | 1.296 |
| O5-N6 | 1.353 | 1.351 | 1.357 | 1.356 | 1.366 |
| O5-N5 | 1.374 | 1.375 | 1.374 | 1.374 | 1.379 |
| N5-C5 | 1.305 | 1.305 | 1.305 | 1.304 | 1.304 |
| C4-C5 | 1.464 | 1.465 | 1.463 | 1.465 | 1.472 |
| C4-N4 | 1.303 | 1.304 | 1.302 | 1.301 | 1.302 |
| O2-N4 | 1.349 | 1.348 | 1.354 | 1.353 | 1.372 |
| O2-N3 | 1.465 | 1.477 | 1.469 | 1.470 | 1.440 |
| Ave. Dev. | 0.0128 | 0.0144 | 0.0134 | 0.0129 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Ji, L.; Jia, X.; Tao, J.; Liu, R.; Wei, D.; Wang, X.; Ji, G. Theoretically Revealing the Response of Intermolecular Vibration Energy Transfer and Decomposition Process of the DNTF System to Electric Fields Using Two-Dimensional Infrared Spectra. Int. J. Mol. Sci. 2023, 24, 4352. https://doi.org/10.3390/ijms24054352
Ren H, Ji L, Jia X, Tao J, Liu R, Wei D, Wang X, Ji G. Theoretically Revealing the Response of Intermolecular Vibration Energy Transfer and Decomposition Process of the DNTF System to Electric Fields Using Two-Dimensional Infrared Spectra. International Journal of Molecular Sciences. 2023; 24(5):4352. https://doi.org/10.3390/ijms24054352
Chicago/Turabian StyleRen, Haichao, Linxiang Ji, Xianzhen Jia, Jun Tao, Ruipeng Liu, Dongqing Wei, Xiaofeng Wang, and Guangfu Ji. 2023. "Theoretically Revealing the Response of Intermolecular Vibration Energy Transfer and Decomposition Process of the DNTF System to Electric Fields Using Two-Dimensional Infrared Spectra" International Journal of Molecular Sciences 24, no. 5: 4352. https://doi.org/10.3390/ijms24054352
APA StyleRen, H., Ji, L., Jia, X., Tao, J., Liu, R., Wei, D., Wang, X., & Ji, G. (2023). Theoretically Revealing the Response of Intermolecular Vibration Energy Transfer and Decomposition Process of the DNTF System to Electric Fields Using Two-Dimensional Infrared Spectra. International Journal of Molecular Sciences, 24(5), 4352. https://doi.org/10.3390/ijms24054352