Binary Fingerprints at Fluctuation-Enhanced Sensing
Abstract
:1. Introduction
2. Binary Patterns for Low Power Consumption
3. An Ultra-Low-Power Realization of the Scheme
4. Experiments with Bacteria and Heated Semiconducting Metal Oxide Sensors
4.1. Sample Preparation
4.2. Experimental Setup [8]
4.3. Types of Samples
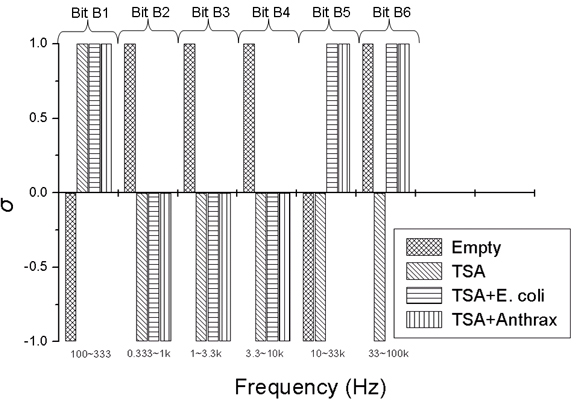
5. Binary Pattern Extracted from Experiments
- Inability to differentiate between the two types of bacteria: the applied sensor and the simple 6 bit pattern generation we used for these tests were unable to differentiate between the two bacteria, while they were able to differentiate between all the other cases (empty, TSA, bacteria). This fact originates from the particular settings of pattern generation because the differences between spectra with different bacteria could be distinguished by naked eye. However, we find this situation satisfactory because our goal was not to present a fully featured/optimized system but to show how much can be achieved with just a simple, ad-hoc, demo version of a 6 bits system.
- Robustness against variations of the bacterium number, see Figure 9. This characteristic was unexpected with Taguchi sensors, which are nonlinear devices, but it could be expected with linear sensors. The most probable reason why we still experienced this property with our sensor is the linear response of nonlinear systems against small perturbations; a situation relevant for Taguchi sensors.
6. Boolean Logic Circuit for Pattern Recognition with Ultra-Low Power Need
7. Power Consumption of the Whole Sensing System
8. Summary
Acknowledgments
References
- Chanda, S. Implications of aerobiology in respiratory allergy. Ann. Agric. Environ. Med 1996, 3, 157–164. [Google Scholar]
- Lacey, J.; Dutkiewicz, J. Bioaerosols and occupational lung disease. J. Aerosol. Sci 1994, 25, 1371–1404. [Google Scholar]
- Eklov, T.; Lundstrom, I. Distributed sensor system for quantification of individual components in a multiple gas mixture. Anal. Chem 1999, 71, 3544–3550. [Google Scholar]
- Gardner, J.W.; Bartlett, P.N. Electronic Noses: Principles and Applications; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Searle, G.E.; Gardner, J.W.; Chappell, M.J.; Godfrey, K.R.; Michael, J.C. System identification of electronic nose data from cyanobacteria experiments. IEEE Sensors J 2002, 2, 218–229. [Google Scholar]
- Ampuero, S.; Bosset, J.O. The electronic nose applied to dairy products: a review. Sens. Actuat. B 2003, 94, 1–12. [Google Scholar]
- Persaud, K.C. Medical applications of odor-sensing devices. New Technol 2005, 4, 50–56. [Google Scholar]
- Chang, H.C.; Kish, L.B.; King, M.D.; Kwan, C. Fluctuation-enhanced sensing of bacterium odors. Sens. Actuat. B 2009, 142, 429–434. [Google Scholar]
- Kish, L.B.; Vajtai, R.; Granqvist, C.G. Extracting information from noise spectra of chemical sensors: single sensor electronic noses and tongues. Sens. Actuat. B 2000, 71, 55. [Google Scholar]
- Kish, L.B.; Granqvist, C.G.; Vajtai, R. Sampling-and-hold chemical sensing by noise measurements for electronic nose applications. Swedish patent 990409-5,. 1999. [Google Scholar]
- Solis, J.L.; Kish, L.B.; Vajtai, R.; Granqvist, C.G.; Olsson, J.; Schnurer, J.; Lantto, V. Nanocrystalline tungsten oxide thick films with high sensitivity to H2S at room temperature. Sens. Actuat. B 2001, 77, 316–321. [Google Scholar]
- Kish, L.B.; Smulko, J.; Heszler, P.; Granqvist, C.G. On the sensitivity, selectivity, sensory information and optimal size of resistive chemical sensors. Nanotechnol. Percept 2007, 3, 43–52. [Google Scholar]
- Smulko, J.M.; Kish, L.B. Higher-order statistics for fluctuation-enhanced gas-sensing. Sensor Mater 2004, 16, 291–299. [Google Scholar]
- Kish, L.B.; Li, Y.; Solis, J.L.; Marlow, W.H.; Vajtai, R.; Granqvist, C.G.; Lantto, V.; Smulko, J.M.; Schmera, G. Detecting harmful gases using fluctuation-enhanced sensing. IEEE Sensors J 2005, 5, 671–676. [Google Scholar]
- Solis, J.L.; Seeton, G.E.; Li, Y.; Kish, L.B. Fluctuation-enhanced multiple-gas sensing. IEEE Sensors J 2005, 5, 1338–1345. [Google Scholar]
- Ederth, J.; Smulko, J.M.; Kish, L.B.; Heszler, P.; Granqvist, C.G. Comparison of classical and fluctuation-enhanced gas sensing with PdxWO3 nanoparticle films. Sens. Actuat. B 2006, 113, 310–315. [Google Scholar]
- Kwan, C.; Schmera, G.; Smulko, J.; Kish, L.B.; Heszler, P.; Granqvist, C.G. Advanced agent identification at fluctuation-enhanced sensing. IEEE Sensors J 2008, 8, 706–713. [Google Scholar]
- Schmera, G.; Kwan, C.; Ajayan, P.; Vajtai, R.; Kish, L.B. Fluctuation-enhanced sensing: Status and perspectives. IEEE Sensors J 2008, 8, 714–719. [Google Scholar]
- Gomri, S.; Seguin, J.L.; Aguir, K. Modelling on oxygen chemisorption induced noise in metallic oxide gas sensors. Sens. Actuat. B 2005, 107, 722–729. [Google Scholar]
- Gomri, S.; Seguin, J.L.; Guerin, J.; Aguir, K. Adsorption–desorption noise in gas sensors: Modelling using langmuir and wolkenstein models for adsorption. Sens. Actuat. B 2006, 114, 451–459. [Google Scholar]
- Solis, J.L.; Hoel, A.; Kish, L.B.; Granqvist, C.G.; Saukko, S.; Lantto, V. Gas-sensing properties of nanocrystalline WO3 films made by advanced reactive gas deposition. J. Am. Ceram. Soc 2001, 84, 1504–1508. [Google Scholar]
- Hoel, A.; Ederth, J.; Kopniczky, J.; Heszler, P.; Kish, L.B.; Olsson, E.; Granqvist, C.G. Conduction invasion noise in nanoparticle WO3/Au thin-film devices for gas sensing application. Smart. Mater. Struct 2002, 11, 640–644. [Google Scholar]
- Sambrook, J.; Fritsch, E.F.; Maniatis, T. Molecular Cloning: A Laboratory Manual’, 2nd ed.; Cold Spring Harbor Laboratory Press: Cold Spring, New York, NY, USA, 1989. [Google Scholar]
- Roger, C.L. Ultra-Low power analog circuits for spike feature extraction and detection from extracellular neural recordings, a dissertation presented to the graduate school of the University of Florida in partial fulfillment of the requirements for the degree of doctor of philosophy, university of Florida, Gainesville, FL, USA. 2007.









| Bit B1 | Bit B2 | Bit B3 | Bit B4 | Bit B5 | Bit B6 | |
|---|---|---|---|---|---|---|
| Empty | 0 | 1 | 1 | 1 | N/A | N/A |
| TSA | 1 | 0 | 0 | 0 | N/A | 0 |
| TSA+bacteria | 1 | 0 | 0 | 0 | N/A | 1 |
| Output of Binary logic | ||
|---|---|---|
| Bit 1 | Bit 2 | |
| Empty | 0 | 0 |
| TSA | 1 | 0 |
| TSA+ Bacteria | 1 | 1 |
©2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/)
Share and Cite
Chang, H.-C.; Kish, L.B.; King, M.D.; Kwan, C. Binary Fingerprints at Fluctuation-Enhanced Sensing. Sensors 2010, 10, 361-373. https://doi.org/10.3390/s100100361
Chang H-C, Kish LB, King MD, Kwan C. Binary Fingerprints at Fluctuation-Enhanced Sensing. Sensors. 2010; 10(1):361-373. https://doi.org/10.3390/s100100361
Chicago/Turabian StyleChang, Hung-Chih, Laszlo B. Kish, Maria D. King, and Chiman Kwan. 2010. "Binary Fingerprints at Fluctuation-Enhanced Sensing" Sensors 10, no. 1: 361-373. https://doi.org/10.3390/s100100361
APA StyleChang, H. -C., Kish, L. B., King, M. D., & Kwan, C. (2010). Binary Fingerprints at Fluctuation-Enhanced Sensing. Sensors, 10(1), 361-373. https://doi.org/10.3390/s100100361