A Novel Wireless Power Transfer-Based Weighed Clustering Cooperative Spectrum Sensing Method for Cognitive Sensor Networks
Abstract
:1. Introduction
- (1)
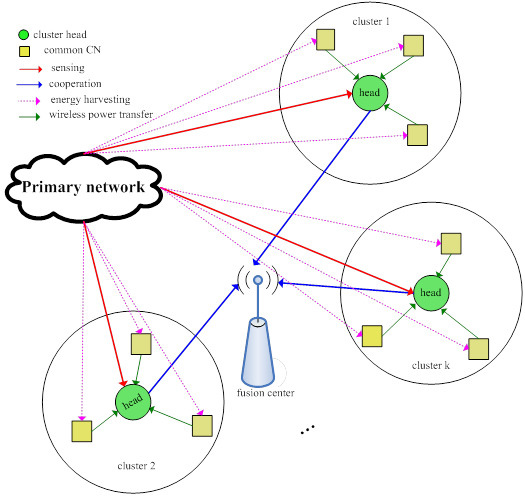
- The paper firstly combines WPT and spectrum sensing and proposes a novel WPT-based weighed clustering spectrum sensing, in which the common CNs of each cluster receive the RF energy of the PN signal that is then transferred to the cluster head, in order to supply the energy consumption of sensing and cooperation of the cluster head.
- (2)
- In our proposed model, fewer nodes will participate in cooperative spectrum sensing, thus the energy and time used for spectrum sensing may decrease greatly. Moreover, the common CNs may transfer the received wireless power to the cooperative nodes, thus the transmission power of the cooperative nodes can be guaranteed.
- (3)
- A joint resource optimization problem is formulated to maximize the spectrum access probability of the CSN through jointly optimizing sensing time and clustering number. With the solutions of the proposed optimization problem, the CSN can obtain larger spectrum access probability while guaranteeing the spectrum sensing performance.
2. Spectrum Sensing Models
| Symbol | Denotation | Symbol | Denotation |
|---|---|---|---|
| received signal by CNi | absence of PN | ||
| presence of PN | PN signal | ||
| power of PN signal | Gaussian noise | ||
| nosie variance | channel gain from PN to CNi | ||
| M | number of signal samples | sampling frequency | |
| sensing time | sensing signal to noise ratio | ||
| sensing threshold | energy statistic | ||
| combined weight | single false alarm probability | ||
| single detection probability | cooperative false alarm probability | ||
| cooperative detection probability | electromagnetism-to-electricity conversion efficiency | ||
| cooperative missed detection probability | BER of the reported sensing information | ||
| D | number of CNs | K | number of cluster heads |
| spectrum access probability | transferred energy of cluster head | ||
| transferred energy of common CN | frame length | ||
| sensing time | average cooperative time overhead | ||
| electricity-to-electromagnetism conversion efficiency | information transmission power |
2.1. Energy Detection
2.2. Weighed Cooperative Spectrum Sensing


3. WPT-Based Clustering Cooperative Spectrum Sensing
3.1. Wireless Power Transfer (WPT)

3.2. Clustering Cooperative Spectrum Sensing

3.3. Cooperative Overhead and Wireless Power Transfer Antenna

3.4. Joint Resource Optimization
| Algorithm 1 Joint optimization of τ and K |
|
4. Clustering Algorithm
| Algorithm2 Clustering algorithm |
|
5. Simulations and Discussion
5.1. Detection Performance Comparison





5.2. Transmission Performance Comparison






6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Haykin, S. Cognitive Radio: Brain-empowered Wireless Communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Ghasemi, A.; Sousa, E.S. Spectrum Sensing in Cognitive Radio Networks: Requirements, Challenges and Design Tradeoffs. IEEE Commun. Mag. 2008, 46, 32–39. [Google Scholar] [CrossRef]
- Lin, Y.E.; Liu, K.H.; Hsieh, H.Y. On Using Interference-Aware Spectrum Sensing for Dynamic Spectrum Access in Cognitive Radio Networks. IEEE Trans. Mob. Comput. 2012, 12, 461–474. [Google Scholar] [CrossRef]
- Singh, J.S.P.; Rai, M.K.; Singh, J. Trade-off between AND and OR Detection Method for Cooperative Sensing in Cognitive Radio. In Proceedings of the IEEE International Advance Computing Conference, Gurgaon, India, 21–22 February 2014; pp. 395–399.
- Shen, J.; Liu, S.; Wang, Y. Robust Energy Detection in Cognitive Radio. IET Commun. 2009, 3, 1016–1023. [Google Scholar] [CrossRef]
- Hamza, D.; Aissa, S.; Aniba, G. Equal Gain Combining for Cooperative Spectrum Sensing in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2014, 13, 4334–4345. [Google Scholar] [CrossRef]
- Zheng, Y.; Xie, X.; Yang, L. Cooperative Spectrum Sensing Based on SNR Comparison in Fusion Center for Cognitive Radio. In Proceedings of the International Conference on Advanced Computer Control, Singapore, 22–24 January 2009; pp. 212–216.
- Mishra, S.M.; Sahai, A.; Brodersen, R.W. Cooperative sensing among cognitive radios. In Proceedings of the IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; pp. 1658–1663.
- Zhi, Q.; Cui, S.G.; Sayed, A.H. Optimal Linear Cooperation for Spectrum Sensing in Cognitive Radio Networks. IEEE J. Sel. Top. Signal Process. 2008, 2, 28–40. [Google Scholar] [CrossRef]
- Liang, Y.C.; Zeng, Y.H.; Peh, E.C.Y. Sensing-throughput Tradeoff for Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2008, 7, 1326–1336. [Google Scholar] [CrossRef]
- Liu, X.; Tan, X. Optimization Algorithm of Periodical Cooperative Spectrum Sensing in Cognitive Radio. Int. J. Commun. Syst. 2014, 27, 705–720. [Google Scholar] [CrossRef]
- Liu, X. A new sensing-throughput trade-off scheme in cooperative multiband cognitive radio network. Int. J. Netw. Manag. 2014, 24, 200–217. [Google Scholar] [CrossRef]
- Waleed, E.; Ghalib, A.S.; Najam, U.H.; Hyung, S.K. Energy and throughput efficient cooperative spectrum sensing in cognitive radio sensor networks. Trans. Emerg. Telecommun. Technol. 2015, 26, 1019–1030. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, W.; Ben, K. Cluster-Based Cooperative Spectrum Sensing in Cognitive Radio Systems. In Proceedings of the IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 2511–2515.
- Chen, C.; Peng, T.; Xu, S. Cooperative Spectrum Sensing with Cluster-Based Architecture in Cognitive Radio Networks. In Proceedings of the IEEE Vehicular Technology Conference, Barcelona, Spain, 26–29 April 2009; pp. 1–5.
- Chaudhari, S.; Lunden, J.; Koivunen, V.; Poor, H.V. Cooperative sensing with imperfect reporting channels: Hard decisions or soft decisions. IEEE Trans. Signal Process. 2012, 60, 18–28. [Google Scholar] [CrossRef]
- Sharma, S.; Bogale, T.; Chatzinotas, S.; Ottersten, B.; Le, L.; Wang, X. Cognitive Radio Techniques under Practical Imperfections: A Survey. IEEE Commun. Surv. Tutor. 2015, in press. [Google Scholar] [CrossRef]
- Sharma, S.K.; Chatzinotas, S.; Ottersten, B. Cooperative Spectrum Sensing for Heterogeneous Sensor Networks Using Multiple Decision Statistics. In Proceedings of the 10th International Conference Cognitive Radio Oriented Wireless Networks (CROWNCOM), Doha, Qatar, 21–23 April 2015.
- Valenta, C.R.; Durgin, G.D. Harvesting Wireless Power: Survey of Energy-Harvester Conversion Efficiency in Far-Field, Wireless Power Transfer Systems. IEEE Microw. Mag. 2014, 15, 108–120. [Google Scholar]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless Information Transfer with Opportunistic Energy Harvesting. IEEE Trans. Wirel. Commun. 2012, 12, 288–300. [Google Scholar] [CrossRef]
- Seunghyun, L.; Zhang, R.; Huang, K. Opportunistic wireless energy harvesting in cognitive Radio networks. IEEE Trans. Wirel. Commun. 2013, 12, 4788–4799. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, Y.; Liu, H. Distributed Consensus-Based Weight Design for Cooperative Spectrum Sensing. IEEE Trans. Parallel Distrib. Syst. 2014, 26, 54–64. [Google Scholar] [CrossRef] [Green Version]
- Ejaz, W.; Najam, U.H.; Kim, H.S. Distributed cooperative spectrum sensing in cognitive radio for ad hoc networks. Comput. Commun. 2013, 36, 1341–1349. [Google Scholar] [CrossRef]
- Liu, X.; Jia, M.; Gu, X.; Tan, X.Z. Optimal Periodic Cooperative Spectrum Sensing Based on Weight Fusion in Cognitive Radio Networks. Sensors 2013, 13, 5251–5272. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Wang, P.; Niyato, D.; Dong, I.K.; Han, Z. Wireless networks with RF energy harvesting: A contemporary survey. IEEE Commun. Surv. Tutor. 2015, 17, 757–789. [Google Scholar] [CrossRef]
- Stephen, B.; Neal, P.; Eric, C. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Najam, U.H.; Ejaz, W.; Kim, H.S. PWAM: Penalty-Based Weight Adjustment Mechanism for Cooperative Spectrum Sensing in Centralized Cognitive Radio Networks. Int. J. Innov. Comput. Inf. Control 2012, 8, 6539–6550. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X. A Novel Wireless Power Transfer-Based Weighed Clustering Cooperative Spectrum Sensing Method for Cognitive Sensor Networks. Sensors 2015, 15, 27760-27782. https://doi.org/10.3390/s151127760
Liu X. A Novel Wireless Power Transfer-Based Weighed Clustering Cooperative Spectrum Sensing Method for Cognitive Sensor Networks. Sensors. 2015; 15(11):27760-27782. https://doi.org/10.3390/s151127760
Chicago/Turabian StyleLiu, Xin. 2015. "A Novel Wireless Power Transfer-Based Weighed Clustering Cooperative Spectrum Sensing Method for Cognitive Sensor Networks" Sensors 15, no. 11: 27760-27782. https://doi.org/10.3390/s151127760
APA StyleLiu, X. (2015). A Novel Wireless Power Transfer-Based Weighed Clustering Cooperative Spectrum Sensing Method for Cognitive Sensor Networks. Sensors, 15(11), 27760-27782. https://doi.org/10.3390/s151127760