Figure 2.
Dimensions of the tank, in mm.
In next subsections, it is shown the behaviour of the power transformer tank implemented considered as rectangular resonant cavity, their theoretical frequency resonances and their measurements when PD activity it is taken into account.
The Tank as a Rectangular Resonant Cavity
A transformer tank is a rectangular structure that has an electromagnetic behaviour as a resonant cavity [
12]. So, when there is PD activity inside the cavity, multiple reflections create stationary waves between its conductive metal walls which generate resonance frequencies. These stationary waves are the transverse magnetic (TM) and transverse electric (TE). TM has no components of magnetic fields in the direction of propagation
= 0, but being nonzero its electric field component,
. While, TE wave, has no components of the electric field in the direction of propagation
= 0, but with nonzero components of magnetic field,
.
To designate the distribution of a stationary wave TM and TE for axis
x,
y,
z of a resonant cavity, subindex
mnp, are used. For the calculation of these modes, the following equation is used [
10,
20]:
where
is the resonance frequency of the cavity,
the permeability of vacuum,
the permittivity of vacuum and
a,
b,
c the dimensions of the tank in
m.
Equation (
2) is used to calculate the frequencies in which the rectangular cavity resonates and to compared these frequencies with their measurement in next subsection.
Assuming that the maximum length of a transformer tank corresponds to the
z-axis propagation, width with the
x-axis and height with the
y-axis, then it is possible to calculate the results of the resonance frequencies
, according to Equation (
2), for transverse electric modes, TE
, and transverse magnetic, TM
. This equation is applied to the tank geometry studied for calculating their resonant frequencies. The first resonance frequency is obtained at 583 MHz.
To have a measure of these frequencies to be compare with its theoretical calculations, the transmission parameter
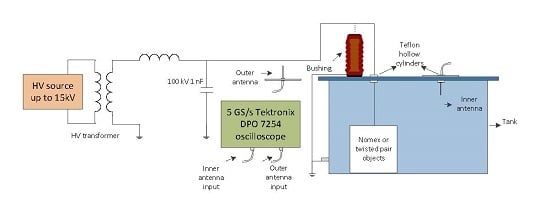
is measure to obtain the frequency response of the tank. For the acquisitions, the Agilent E8364B network analyser and two antennas are used, thus, one injects energy in the tank by sweeping the frequency of the NA between 500 MHz and 2500 MHz and the other acts as a receiver.
Figure 3 shows the positions of the antennas deployed inside the tank through the cavities on the top cover.
Figure 3.
Two 10 cm monopole antennas with ground plane and an Agilent E8364BD network analyser for the measurement of the parameter of the tank.
Figure 3.
Two 10 cm monopole antennas with ground plane and an Agilent E8364BD network analyser for the measurement of the parameter of the tank.
In
Figure 4 the
parameter measured with two 10 cm monopoles with ground plane together with the network analyser is shown.
Figure 4.
parameter (frequency response of the tank) measured with two 10 cm dipoles.
Figure 4.
parameter (frequency response of the tank) measured with two 10 cm dipoles.
The calculated frequency resonances, their modes, the resonances measured
(MHz), their power (dB) and the ER between frequencies calculated and measured are shown in
Table 3 up to 2000 MHz. When there is no mode or no measurement of a resonance frequency it is represented by a dash (−) in
Table 3.
Table 3.
Frequency resonances for a 30 × 30 × 50 cm cavity in 500–2000 MHz.
Table 3.
Frequency resonances for a 30 × 30 × 50 cm cavity in 500–2000 MHz.
| (MHz) Calculated | TM
| TE
| (MHz) Measured | Power (dB) | RE (%) | (MHz) Calculated | TM
| TE
| (MHz) Measured | Power(dB) | RE (%) |
|---|
| 583 | − | 011, 101 | 560 | −26 | 3.89 | 1535 | 222 | 222 | 1540 | −15 | −0.31 |
| 707 | 110 | − | 655 | −41 | 7.30 | 1561 | − | 024, 204 | 1552, 1560 | −10, −6 | 0.57, 0.06 |
| 768 | 111 | 111 | 765 | −11 | 0.34 | 1580 | 130, 310 | 015, 105 | 1578, 1590 | −7, −6 | 0.13, −0.63 |
| 780 | − | 012, 102 | 787 | −43 | −0.83 | 1608 | 131, 311 | 131, 311 | 1602 | −8 | 0.39 |
| 927 | 112 | 112 | 967 | −29 | −4.35 | 1614 | 032, 302 | − | 1620 | −17 | −0.34 |
| 1029 | − | 013, 103 | 1032 | −8 | −0.31 | 1639 | 124, 214 | 124, 214 | 1628, 1635 | −15, −10 | 0.67, 0.24 |
| 1043 | − | 021, 201 | 1048 | −6 | −0.45 | 1657 | 115 | 115 | 1658 | −11 | −0.05 |
| 1117 | 120, 210 | − | 1105, 1122 | −6, −35 | 1.10, −0.42 | 1675 | 225 | 225 | 1665 | −6 | 0.61 |
| 1144 | 113 | 113 | 1145 | −8 | −0.11 | 1690 | 132, 312 | 132, 312 | 1688 | −23 | 0.12 |
| 1157 | 121, 211 | 121, 211 | 1165 | −12 | −0.71 | 1748 | − | 033, 303 | 1778 | −34 | −1.71 |
| 1165 | − | 022, 202 | 1180, 1222 | −29, −10 | −1.25, −4.86 | 1802 | 230, 320 | 025, 205 | − | − | − |
| 1268 | 122, 212 | 122, 212 | 1270 | −6 | −0.16 | 1818 | 133, 313 | 133, 313 | − | − | − |
| 1299 | − | 014, 104 | 1285, 1310 | −7, −24 | 1.09, −0.84 | 1826 | 231, 321 | 231, 321 | 1842 | −14 | −0.86 |
| 1344 | − | 023, 203 | 1348 | −5 | −0.27 | 1853 | 224 | 224 | 1842 | −14 | 0.62 |
| 1392 | 114 | 114 | 1402 | −13 | −0.73 | 1867 | − | 016, 106 | 1860 | −43 | 0.37 |
| 1413 | 220 | − | − | − | − | 1870 | 125, 215 | 125, 215 | − | − | − |
| 1434 | 123, 213 | 123, 213 | 1435 | −8 | −0.05 | 1899 | 232, 322 | 232, 322 | 1902 | −12 | −0.17 |
| 1445 | 221 | 221 | − | − | − | 1920 | − | 034, 304 | − | − | − |
| 1529 | − | 031, 301 | 1522 | −10 | 0.43 | 1933 | 116 | 116 | 1932 | −23 | −0.03 |
Experimentally, almost all modes calculated theoretically are obtained, except at high-frequencies, where resonances are not reproduced.
The dominant resonance mode corresponds to TE and TE. The first resonance for the dominant transverse mode corresponds to TM. In this cavity, these modes are reproduced at 583 MHz and 707 MHz, TE and TM, respectively. When they are measured with the network analyser, the first TE mode is obtained at 560 MHz with a RE of 3.89%, compared with the theoretical values, and dB, where the negative value indicates emitted power inside the tank. Besides, the first TM mode has its resonance frequency at 655 MHz with a RE of 7.30% and power of dB, this high energy value received, is because the antenna has its first resonance at 640 MHz as it is mentioned above.
As it is shown in
Figure 4, experimentally, not all modes are excited in the resonant cavity for frequencies above 2300 MHz. Assuming that the network analyser emits the same power at all frequencies, then the receiving or transmitting antenna, are not able to excite the frequencies within the tank. However, for lower frequencies, the tank is capable of resonating in the most theoretically calculated modes in
Table 3.
When the tank resonance modes are measured, there are mainly two factors that affect the result. First, the modes defined by the structure. To obtain these resonances, a frequency sweep is done with the network analyser up to 2500 MHz. The second is the frequency response of the antenna used, that must be matched for all the bandwidth required. However, the hole size to accommodate the antenna on the tank and its geometry do not allow to deploy an antenna that meets these requirements. By restriction of size, and to have a cheaper antenna than a disc-coupler to do the measures, a monopole antenna is used because can also be deployed inside the empty model tank through the holes and can acquire energy up to 2250 MHz for the 10 cm in length antenna.
In the experimental measurements with the transformer tank model, almost all their own theoretical frequencies of a rectangular resonant cavity of the same dimensions are obtained, as shown in
Table 3 [
10]. To study only the effect that the tank has on PD propagation, the tank model unfilled of oil and without placing a magnetic core and windings therein it is used for measuring discharge with the antennas. Inside, it is expected to measure the direct wave of the discharge and the pulses reflected in the shield walls that excite their resonant frequencies. Outside, it is intended to receive power content from frequencies with the higher energy, mitigated by the enclosure, which goes through the holes in the top and the joints between the cover and the walls. These components depend on the frequency response of the test object emitting and the resonance frequencies that allows the cavity.