Enhanced ICP for the Registration of Large-Scale 3D Environment Models: An Experimental Study
Abstract
:1. Introduction
2. Preliminaries
3. New Proposed Registration Algorithm
- Step I.
- Point cloud standardization and extraction

- Step II.
- Coarse to fine iteration
- (a)
- Align the scan point cloud P and model point cloud Q at the current resolution level.
- (b)
- Calculate the efficiency of the current ICP registration by using the registration index Ikcur and tendency index Trendkcur, where k represents the kth resolution level and cur represents the current ICP registration.
- Step III.
- Early warning mechanism
- (a)
- Adjust the resolution level based on the value of Trendkcur.
- (b)
- If Trendkcur is bigger than a given positive threshold, go directly to Step II. If Trendkcur is just bigger than zero, update the resolution to a higher level and then go to Step II.
- (c)
- If Ikcur is bigger than the given threshold, the algorithm has found a global optimal result, and go to Step V. Otherwise, the early warning has been triggered, and go to Step IV.
- Step IV.
- Heuristic escape
- (a)
- Cluster the current aligned scan point cloud P based on distances between each point in P with its closest point in the model point cloud Q. Then, extract the biggest clustered point cloud Pmerge with the distance below the given threshold Threscluster.
- (b)
- Estimate the normal vector and normal surface of the point cloud Pmerge and transform the current scan point cloud into six temporary scan point clouds P(n)temp, where n is from 1 to 6;
- (c)
- Weight each transformation vectors according to the registration index at each temporary scan point cloud P(n)temp and generate the transformation vector according to the ICP registration.
- (d)
- Estimate the potential translation Tescape based on the weighted translation vectors and then transform the scan point cloud P according to the estimated translation vector. Go to Step III.
3.1. Octree-Based 3D Map Extraction
3.2. Early Warning Mechanism
3.3. Heuristic Escape

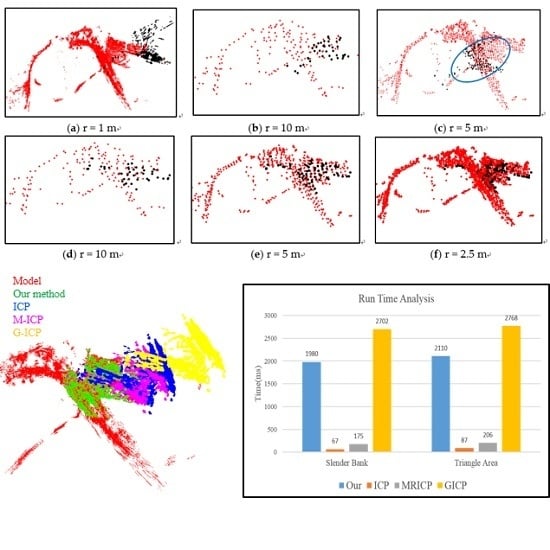
4. Experiments and Results
4.1. Experiment Setup

| No. | Datasets | Number of Points | Resolution |
|---|---|---|---|
| Slender bank | |||
| ExI | Model | 212,912 | 1 m |
| Scan | 40,300 | 0.5 m | |
| Triangular area | |||
| ExII | Model | 212,912 | 1 m |
| Scan | 125,493 | 0.2 m | |

4.2. Multi-Resolution Map Generation

4.3. Warning and Escape



4.4. Convergence

| Method | Translation Error et | Rotation Error er | ||||
|---|---|---|---|---|---|---|
| min | μt | σt | min | μr | σr | |
| Slender Bank Experiment | ||||||
| ICP | 1.45 m | 8.34 m | 6.32 m | 3.4° | 24.1° | 10.2° |
| M-ICP | 1.55 m | 6.57 m | 4.31 m | 1.6° | 15.8° | 5.9° |
| G-ICP | 0.45 m | 5.11 m | 2.31 m | 0.2° | 12.09° | 3.8° |
| OUR | 0.23 m | 1.78 m | 1.98 m | 0.4° | 1.7° | 1.2° |
| Triangular area Experiment | ||||||
| ICP | 1.24 m | 8.23 m | 9.21 m | 2.3° | 19.4° | 12.2° |
| M-ICP | 1.77 m | 5.34 m | 6.53 m | 2.1° | 15.4° | 8.6° |
| G-ICP | 0.30 m | 4.23 m | 3.34 m | 0.5° | 12.7° | 6.1° |
| OUR | 0.10 m | 1.32 m | 1.42 m | 1.1° | 2.8° | 1.8° |

| Method | Translation Error et | Rotation Error er | ||||
|---|---|---|---|---|---|---|
| min | μt | σt | min | μr | σr | |
| Slender bank experiment | ||||||
| ICP | 17.21 m | 24.23 m | 16.32 m | 154.4° | 176.1° | 21.2° |
| M-ICP | 13.23 m | 21.23 m | 18.31 m | 156.6° | 182.8° | 33.9° |
| G-ICP | 10.32 m | 15.21 m | 12.11 m | 126.4° | 192.09° | 45.8° |
| OUR | 0.31 m | 4.55 m | 3.98 m | 0.1° | 15.7° | 8.2° |
| Triangular area experiment | ||||||
| ICP | 7.32 m | 23.34 m | 16.21 m | 126.4° | 189.1° | 28.2° |
| M-ICP | 16.42 m | 26.57 m | 15.31 m | 145.6° | 176.8° | 35.9° |
| G-ICP | 9.89 m | 28.11 m | 13.23 m | 170.2° | 181.9° | 49.8° |
| OUR | 0.21 m | 6.78 m | 4.98 m | 0.4° | 14.7° | 7.4° |
4.5. Running Time

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Du, M.; Xing, Y.; Suo, J.; Liu, B.; Jia, N.; Huo, R.; Chen, C.; Liu, Y. Real-time automatic hospital-wide surveillance of nosocomial infections and outbreaks in a large Chinese tertiary hospital. BMC Med. Inform. Decis. Mak. 2014, 14. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Daniel, E.; Hunter, A.A.; Xiao, R.; Gao, J.; Li, H.; Maguire, M.G.; Brainard, D.H.; Gee, J.C. Landmark matching based retinal image alignment by enforcing sparsity in correspondence matrix. Med. Image Anal. 2014, 18, 903–913. [Google Scholar] [CrossRef] [PubMed]
- Handa, A.; Whelan, T.; McDonald, J.; Davison, A.J. A Benchmark for RGB-D Visual Odometry, 3D Reconstruction and SLAM. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 1524–1531.
- Salas-Moreno, R.F.; Glocken, B.; Kelly, P.H.J.; Davison, A.J. Dense Planar SLAM. In Proceedings of the IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Munich, Germany, 10–12 September 2014; pp. 157–164.
- Jiang, Y.; Chen, H.; Xiong, G.; Scaramuzza, D. ICP Stereo Visual Odometry for Wheeled Vehicles based on a 1DOF Motion Prior. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 585–592.
- Nießner, M.; Dai, A.; Fisher, M. Combining inertial navigation and ICP for real-time 3D surface reconstruction. Available online: http://graphics.stanford.edu/~niessner/papers/2014/0inertia/niessner2014combining.pdf (accessed on 22 January 2016).
- David, G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar]
- Smith, S.M.; Brady, J.M. SUSAN—A new approach to low level image processing. Int. J. Comput. Vis. 1997, 23, 45–78. [Google Scholar] [CrossRef]
- Johnson, A. Spin-Images: A Representation for 3-D Surface Matching. Doctoral Dissertation, Carnegie Mellon University, Pittsburgh, PA, USA, 1997; pp. 1–7. [Google Scholar]
- He, Y.; Mei, Y. An efficient registration algorithm based on spin image for LiDAR 3D point cloud models. Neurocomputing 2015, 151, 354–363. [Google Scholar] [CrossRef]
- Dinh, H.Q.; Kropac, S. Multi-resolution Spin-images. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; Volume 1, pp. 863–870.
- Assfalg, J.; Bertini, M.; Bimbo, A.D.; Pala, P. Content-based retrieval of 3-D objects using spin image signatures. IEEE Trans. Multimed. 2007, 9, 589–599. [Google Scholar] [CrossRef]
- Bao, S.Y.; Chandraker, M.; Lin, Y.; Savarese, S. Dense Object Reconstruction with Semantic Priors. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1264–1271.
- Ho, H.T.; Gibbins, D. Curvature-based approach for multi-scale feature extraction from 3D meshes and unstructured point clouds. IET Comput. Vis. 2009, 3, 201–212. [Google Scholar] [CrossRef]
- Besl, P.; McKay, N. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object Modelling by Registration of Multiple Range Images. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume CH2969, pp. 2724–2729.
- Zhang, Z. Iterative point matching for registration of free-form curves and surfaces. Int. J. Comput. Vis. 1994, 13, 119–152. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-ICP. Available online: http://www.robots.ox.ac.uk/~avsegal/resources/papers/Generalized_ICP.pdf (accessed on 22 January 2016).
- Jost, T.; Hugli, H. A Multi-resolution ICP with Heuristic Closest Point Search for Fast and Robust 3D Registration of Range Images. In Proceedings of the Fourth International Conference on 3-D Digital Imaging Modeling, Banff, AB, Canada, 6–10 October 2003.
- Jost, T.; Hugli, H. A Multi-resolution Scheme ICP Algorithm for Fast Shape Registration. In Proceedings of the First International Symposium on 3D Data Processing, Visualization and Transmission, Padova, Italy, 19–21 June 2002; pp. 2000–2003.
- Yang, J.; Li, H.; Jia, Y. Go-ICP: Solving 3D Registration Efficiently and Globally Optimally. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1457–1464.
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Zeng, M.; Zhao, F.; Zheng, J.; Liu, X. Octree-based fusion for real-time 3D reconstruction. Graph. Model. 2013, 75, 126–136. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D Registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009.
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Berger, E.; Wheeler, R.; Mg, A. ROS: An Open-Source Robot Operating System. Available online: http://pub1.willowgarage.com/~konolige/cs225B/docs/quigley-icra2009-ros.pdf (accessed on 22 January 2016).
- Rusu, R.B.; Cousins, S. 3D Is Here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Yin, P.; He, Y.; Gu, F. Enhanced ICP for the Registration of Large-Scale 3D Environment Models: An Experimental Study. Sensors 2016, 16, 228. https://doi.org/10.3390/s16020228
Han J, Yin P, He Y, Gu F. Enhanced ICP for the Registration of Large-Scale 3D Environment Models: An Experimental Study. Sensors. 2016; 16(2):228. https://doi.org/10.3390/s16020228
Chicago/Turabian StyleHan, Jianda, Peng Yin, Yuqing He, and Feng Gu. 2016. "Enhanced ICP for the Registration of Large-Scale 3D Environment Models: An Experimental Study" Sensors 16, no. 2: 228. https://doi.org/10.3390/s16020228
APA StyleHan, J., Yin, P., He, Y., & Gu, F. (2016). Enhanced ICP for the Registration of Large-Scale 3D Environment Models: An Experimental Study. Sensors, 16(2), 228. https://doi.org/10.3390/s16020228