1. Introduction
Radionuclide imaging has become one of the most advanced molecular imaging techniques to monitor physiological functions [
1,
2]. However, Single Photon Emission Computed Tomography (SPECT) images tend to be “noisy” because of the low amount of radiotracer per volume of interest (VOI) and the effect of Compton scattering in tissue and collimators. Over the past decades, researchers have been dedicated to developing gamma-cameras with improved spatial resolution and energy resolution. Semiconductor nuclear radiation detectors, especially cadmium zinc telluride (Cd
1−xZn
xTe, CZT) materials, have been considered as alternatives to scintillator detectors [
3,
4,
5] because of their good stopping power and low dark current [
4,
6,
7]. Notably, the major advantage of semiconductor over traditional scintillator detectors is that they can directly convert the deposited photon energy into measurable signals, which could improve energy resolution and detection efficiency [
4,
5,
7,
8]. Hence, CZT detectors are regarded to be the most promising option for SPECT imaging.
The CZT detector consists of a semiconducting crystal that is bump-bonded to a large area ASIC and packaged with a high performance data acquisition system. Recently, great progress has been made in electronics [
9,
10,
11,
12] and crystal growing [
13,
14]. However, there are still some defective pixels, showing degraded features, such as split or broadening spectral peaks and extraordinarily low or high response, especially for pixels with smaller sizes or at the edge of module. Though the defective pixels only occupy a small proportion of each module, separate defects of each module may cluster to form continuous defective regions if several modules are arranged into a large detector, as shown in
Figure 1. The continuous defective region in detector occurs in projections and introduces ring artefacts [
15] after reconstruction, which degrades image quality and may lead to misinterpretation, e.g., misdiagnosis or overdiagnosis [
16].
Interpolation is a common correction method for defective pixels, which may work well for separate or individual bad pixels in homogeneous regions. For bad pixel cluster regions, however, simple interpolation often leads to inaccurate estimations. The determination of interpolation direction also poses more complexity since there are many variations for the constellation of defective pixels. Moreover, the advantage of interpolation method vanishes when the pixel size is small [
17]. A proposed alternative plan is using sinogram-processing to eliminate the ring artifacts. Nonetheless, the 2D-wavelet-analysis [
18] and polyphase decomposition in sinogram process [
19] may introduce some noise or artifacts, and it has higher numerical complexity.
In this paper, an advanced wobbling method is proposed to correct the defective pixels. In order to accomplish the correction method and demonstrate its effects, we built a CZT SPECT system equipped with a simple mechanical device and conduct phantom experiment. The correction method is applied to various constellations of defective pixels. The correction effectiveness is evaluated quantitatively and is compared with conventional interpolation method. The results proved that the proposed wobbling method provides improvement in image quality of pixelated semiconductor detector, especially for the small object imaging with pinhole collimator.
2. Materials and Methods
2.1. Wobbling Correction Method
The wobbling method mainly includes following four steps:
2.1.1. 1st Step: Uniformity Correction and Wobbling Path Planning
The uniformity corrections are conducted by flood phantom first. From the flood image, some continuous bad pixels, which would affect image quality and cause ring artifacts after reconstruction, have been localized. Then all of defective pixels are recognized and the wobbling path is defined.
2.1.2. 2nd Step: Acquisition of the Wobbling Images
The basis of the wobbling correction method is the acquisition of wobbling images. Typically, it acquires different observations of the same object,
i.e., images with shifts of several pixel dimensions.
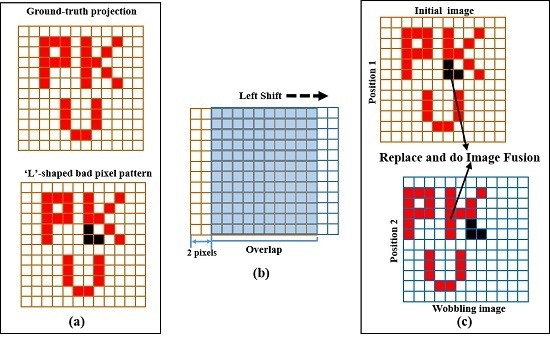
Figure 2 shows an example of wobbling acquisition for the method. It is assumed that the projection on the detector is a “PKU”-shaped image and an “L”-shaped bad pixel pattern exists on CZT detector, as shown in
Figure 2a. The detector performs a scan at Position 1 and subsequently acquires a wobbling image after a left shift of two pixel dimension in the horizontal direction (
Figure 2b). In this way, we get the related images (“twin images”, as shown in
Figure 2c). Each of the wobbling images contributes useful information to the final corrected image and its correlation will be illustrated in the following 3rd Step.
The wobbling acquisition can perform vertical and horizontal movement according to the defective-pixel patterns. In this paper, we mainly considered two-pixel shifts to correct defective pixels, so that there are 72.5% overlap between the two related images.
2.1.3. 3rd Step: Registration of Images Obtained from the Wobbling Method
After wobbling acquisition, each projection has two samples (images A and B), which respectively represent the initial and wobbling images, regarding the same imaging object.
and
are the number of emitted photons which are detected by each pixel.
means pixel index. The correlation between
fA and
fB can be expressed as a general rigid-body transformation that includes a combination of rotation and translation:
where
and
is the translate transformation and rotate transformation between
and
. A rigid-body transformation is applicable provided the pixel size of the CZT detector is negligible compared with the accuracy of the linear translation stage.
2.1.4. 4th Step: Replace the Defective Pixels and Apply an Image Fusion Algorithm
After establishing the point-to-point correspondence of
and
, we replace defective pixels using their counterparts and apply an image fusion algorithm to the two related images. The basic case of two roughly aligned images
and
with the overlapped area Ω is shown in
Figure 3. In this paper, we mainly investigate the following two approaches to produce the mosaic image
IΩ:
- (1)
Simple averaging function(Fusion method A):
- (2)
Distance weighted function(Fusion method B):
where σ(0 ≤ σ ≤ 1) is the transition factor, as shown in
Figure 3, based on the distance of the current pixel coordinate from its own boundary.
The trade-off relationship between image quality and acquisition time is also considered here. Compared with the common acquisition mode, the acquisition time of each scan in the wobbling method is halved for two positions. In this way, the wobbling method can acquire sufficient counts without extending the data acquisition time. In this study, we are mainly interested in how to correct fixed defective pixels and edge-effects in CZT detectors, other defects such as geometric deformation, noise corruption and subsequent reconstruction algorithms, are not considered here.
2.2. System Description
The pinhole SPECT system is developed based on a CZT-detector and aiming for small animal imaging. The system, as shown in
Figure 4, contains the detector, pinhole collimator and rotation stage where imaging objects are placed. The single pinhole collimator is made of tungsten alloy (ρ = 18.5 g/cm
3), with 0.8 mm aperture diameter, 1.38 mm channel height, and 60° opening angle. A linear translation stage is installed underneath the detector that provides support for the detector and the drive for wobble motion. It allows linear movement along the X, Y axes within a 50 mm range and its precision can reach 20 μm. The stage contains a grating ruler, which gives the feedback of motion position and guarantees the precision. With the translation stage, the wobbling range of detector can be adjusted from 0.25 to 50 mm in steps of 0.25 mm. The movement of linear stage is controlled by dedicated C++ codes, which are integrated into the acquisition software. After the first position the detector performs a scan and is subsequently wobbled for the following acquisition. Each scan is saved for post-processing according to the described wobbling method in
Figure 2. A standard M1522 CZT detector module (
Figure 4), has an active region of 40 × 40 mm
2 and 5 mm thick with Au contact (Redlen Technologies Inc., Saanichton, BC , Canada) was used in this work. The module is organized in a 16 × 16 array with a 2.46 mm pixel pitch and its acquisition software provides pixel position and energy value in a binary format. Energy resolution of this module is typical about 6.5% (Co-57 source).
2.3. Phantom Experiment
2.3.1. Flood Image Experiment
Flood images are obtained to check the performance of the CZT detector. We arranged four CZT modules into a 2 × 2 array, resulting in an 80 × 80 mm2 detection area. It was exposed to a Tc-99m flood source with 2.22 mCi for 3600 s. The flood images are obtained with the 15% energy window (140 keV). The uniformity and energy spectrum of individual pixel as well as whole entire detector have been analyzed.
2.3.2. Line Source Phantom Experiment
To evaluate the performance of the proposed correction method, line source phantom experiment is designed as shown in
Figure 5.
Four line sources (2 mm inner diameter) are placed off-axis, symmetrically on the two sides of axis of rotation (AOR) which is 60 mm away from the aperture (120 mm from the detector surface). The center distance between each source is 4 mm. This geometric configuration approximately results in 2× magnification. Each line source is filled with 2.6 mCi/mL Tc-99m labelled medronate (MDP). After data acquisition, the correction and evaluation processes are performed by a Matlab-based program.
2.4. Image Quality Evaluation
Aiming at evaluating the effect of our wobbling correction method, we conducted phantom experiments and compared the results with a conventional correction method. Firstly, line sources are scanned statically as reference images. On the reference images, we deliberately defined some pixels as bad pixels and set the counts as zero, resulting in the image waiting to be corrected (identified as “bad image” in the following). Correction methods are applied to various bad-pixel patterns such as: (1) two bad pixels (vertical); (2) two bad pixels (horizontal); (3) three bad pixels; (4) four bad pixels. Here, we mainly investigate the effect of the wobbling method in the correction of bad pixels that appear in the region of interest (ROI) and appear in the background. We defined the effectiveness of a correction method as the similarity between the corrected image (C) and reference image (R). The similarity is assessed using peak signal-to-noise ratio (PSNR) and structural similarity (SSIM), which are the widely used full-reference quality metrics [
20,
21]. Given the reference image R and the corrected image C, both of size M × N, the PSNR between C and R is defined as:
where:
When MSE, which is short for mean squared error, approaches zero, the PSNR value approaches infinity, thus a higher PSNR value provides a higher image quality.
The SSIM is a well-known quality metric used to assess the similarity between two image, considering a combination of three factors that loss of correlation, luminance distortion and contrast distortion. The SSIM is defined as:
where l(C, R) is the luminance comparison function, c(C, R) is contrast comparison function, and s(C, R) is structure comparison function and they are calculated as following equations:
Moreover, α, β, γ in Equation (7) are parameters used to adjust the relative importance of the three factors and the positive values constants c1, c2, c3 are used to avoid a null denominator. In order to simplify the expression, we set α = β = γ = 1 and c1 = c2 = 2c3 in this paper. We use PSNR to assess the correction effect of pixels that appeared in ROI and use SSIM in terms of bad pixels appearing in the background. Here, we execute the wobbling correction method using averaging and distance-weighting fusion models (mentioned as “Method A” and “Method B”) and compare the results with a conventional interpolation correction method.
4. Discussion
According to the evaluation factor defined in
Section 2.4, the PSNR and SSIM are calculated for various bad pixel conditions with different pixel numbers and arrangements. The PSNR results of bad pixels appearing in the ROI are listed in
Table 1. The SSIM results, assessing the correction effect for background bad pixels, are listed in
Table 2. The improvements of the wobbling methods A and B compared with the conventional interpolation method are also marked in
Table 1 and
Table 2. In order to demonstrate the improvement of the wobbling correction method explicitly, the PSNR and SSIM values of different correction methods for various bad-pixel numbers are plotted in
Figure 9 and
Figure 10, respectively.
The proposed wobbling correction method results in higher PSNR and SSIM, in particular when there are more than two continuous bad pixels. For the condition where bad pixels appear in the ROI, the improvement of the wobbling method results is around 10%~20% when the number of bad pixels is less than three. As the number of continuous bad pixels gets larger, he PSNR of the proposed wobbling method is significantly higher. For three continuous bad pixels, the PSNR of the wobbling method A and B is 1.6 and 1.5 times higher than the interpolation result. According to
Table 2 of SSIM results, the overall improvement of the wobbling method is 10% for correction of background bad pixels, compared with conventional interpolation. As can be seen in
Figure 8 and
Figure 9, defects up to 4 bad pixels can be corrected almost flawlessly when the wobbling correction is used. Conventional interpolation may already be inadequate for bad-pixel numbers up to four. This is because the conventional interpolation method is based on using the neighboring pixels to estimate the bad pixels’ counts. When the defects cluster to form large regions of corrected pixels, the neighboring information is not sufficient for the correction, whereas the proposed method acquires two images of related wobbling positions, which can provide a comprehensive reference for correction, so the wobbling method is still effective when there are large defective regions. Moreover, the proper fusion model in the wobbling method can make effective use of the two wobbling images, producing desirable correction results.
5. Conclusions
In this paper, we propose a novel method for correcting continuous bad pixels. Within the same acquisition time, images of two wobbling positions provide a reference for reasonable correction. We conduct corrections for various bad pixel conditions and use PSNR and SSIM estimators to evaluate the correction results. In the phantom experiment, the conventional interpolation method is used for comparison. The results show that wobbling method can correct continuous bad pixels effectively, no matter whether they appear in the ROI or background, whereas, a conventional interpolation method cannot effectively recover the original information, especially when there are more than three continuous bad pixels. In our future study, a proper image fusion algorithm of the wobbling images can be further investigated, resulting in a more effective correction. The wobbling method is conceptually simple, computationally efficient, and easy to use. Furthermore, this correction technique is potentially applicable to the standard pixelated detector, such as Si, GaAs and CdTe, with a proper motorized system.