A Reliability-Based Method to Sensor Data Fusion
Abstract
:1. Introduction
2. Preliminaries
2.1. Dempster–Shafer Evidence Theory
2.1.1. Frame of Discernment
2.1.2. Mass Function
2.1.3. Dempster’s Combination Rule
2.1.4. Discounting
2.2. Pignistic Probability
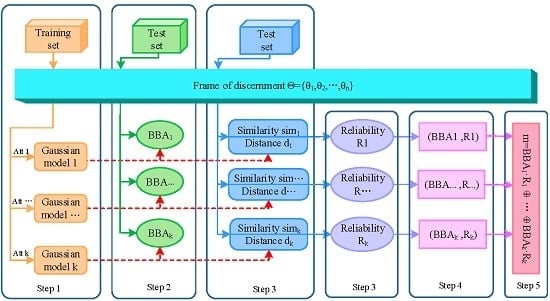
3. The Proposed Method
3.1. The Modeling of Each Attribute
- Suppose that there are n classes, namely the frame of discernment . Each class has k attributes.
- For the training samples of class in the j-th attribute, the mean value and the standard deviation are calculated respectively as follows:where and . N is the training sample size of class . is the attribute value of the j-th attribute from the l-th training sample in class .
- The Gaussian membership function of the j-th attribute of class is generated as follows:where , and .
3.2. Reliability-Based BBA Generation Method
3.2.1. The Determination of BBA
3.2.2. The Measurement of the Reliability of BBA
3.3. Sensor Data Fusion
4. Numerical Example
4.1. Experiments on Two Datasets: Five-Fold Cross-Validation
4.2. An Application Example of Fault Diagnosis
- Based on the idea of the Z-number, an ordered pair is proposed to represent BBA along with its associated reliability. The first component is a mass function; the second component R is a measurement of the reliability of the first component. According to this ordered pair, the reliability of BBA can be measured well at the stage of BBA generation.
- In the process of measuring the reliability of BBA, the information about two things is taken into account. One is the similarity among classes (static information). Another is the risk distance between the test samples and the overlapping area among classes (dynamic information). This makes the results truer and more credible.
- The proposed method is based on a feasible method of measuring the reliability of BBA, which can be replaced with other measure methods for different applications. Namely, this method is flexible and easy to extend in many applications.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Experimental Data of Fault Diagnosis
| Groups | Observations | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X11 | 0.1663 | 0.1590 | 0.1568 | 0.1485 | 0.1723 | 0.2006 | 0.1903 | 0.1908 | 0.1986 | 0.1843 |
| 0.1785 | 0.1610 | 0.1579 | 0.1511 | 0.1532 | 0.1647 | 0.1628 | 0.1646 | 0.1634 | 0.1642 | |
| 0.1648 | 0.1640 | 0.1674 | 0.0661 | 0.1659 | 0.1650 | 0.1633 | 0.1632 | 0.1604 | 0.1542 | |
| 0.1555 | 0.1562 | 0.1540 | 0.1564 | 0.1557 | 0.1542 | 0.1546 | 0.1571 | 0.1537 | 0.1536 | |
| X12 | 0.154 | 0.1518 | 0.1537 | 0.1548 | 0.1542 | 0.1538 | 0.1545 | 0.1537 | 0.1571 | 0.1560 |
| 0.1584 | 0.1552 | 0.1586 | 0.1574 | 0.1569 | 0.1565 | 0.1551 | 0.1585 | 0.1585 | 0.1593 | |
| 0.1548 | 0.1558 | 0.1547 | 0.1593 | 0.1532 | 0.1632 | 0.1575 | 0.159 | 0.1594 | 0.1541 | |
| 0.165 | 0.1674 | 0.1651 | 0.1604 | 0.1787 | 0.1818 | 0.1820 | 0.1656 | 0.1658 | 0.1644 | |
| X13 | 0.1647 | 0.1647 | 0.1654 | 0.1651 | 0.1656 | 0.1653 | 0.1652 | 0.1652 | 0.1648 | 0.1649 |
| 0.1653 | 0.1650 | 0.1650 | 0.1652 | 0.1653 | 0.1652 | 0.1648 | 0.1647 | 0.1646 | 0.1645 | |
| 0.1651 | 0.1652 | 0.1652 | 0.1649 | 0.1650 | 0.1643 | 0.1640 | 0.1639 | 0.1641 | 0.1633 | |
| 0.1632 | 0.1629 | 0.1630 | 0.1630 | 0.1634 | 0.1631 | 0.1634 | 0.1629 | 0.1632 | 0.1629 | |
| X14 | 0.1630 | 0.1629 | 0.1627 | 0.1626 | 0.1622 | 0.1624 | 0.1627 | 0.1618 | 0.1614 | 0.1617 |
| 0.1621 | 0.1615 | 0.1618 | 0.1611 | 0.1614 | 0.1610 | 0.1612 | 0.1611 | 0.1616 | 0.1612 | |
| 0.1612 | 0.1613 | 0.1623 | 0.1616 | 0.1621 | 0.1613 | 0.1611 | 0.1610 | 0.1610 | 0.1613 | |
| 0.1615 | 0.1616 | 0.1618 | 0.1616 | 0.1614 | 0.1612 | 0.1606 | 0.1614 | 0.1619 | 0.1614 | |
| X15 | 0.1609 | 0.1610 | 0.1612 | 0.1615 | 0.1609 | 0.1606 | 0.1604 | 0.1606 | 0.1605 | 0.1601 |
| 0.1604 | 0.1608 | 0.1610 | 0.1603 | 0.1599 | 0.1601 | 0.1602 | 0.1599 | 0.1598 | 0.1598 | |
| 0.1598 | 0.1596 | 0.1595 | 0.1593 | 0.1594 | 0.1598 | 0.1596 | 0.1597 | 0.1595 | 0.1593 | |
| 0.1598 | 0.1596 | 0.1597 | 0.1595 | 0.1593 | 0.1577 | 0.1580 | 0.1576 | 0.1577 | 0.1579 | |
| X21 | 0.1612 | 0.1620 | 0.1612 | 0.1610 | 0.1385 | 0.1222 | 0.1475 | 0.1306 | 0.1210 | 0.1501 |
| 0.1548 | 0.1577 | 0.1622 | 0.1618 | 0.1621 | 0.1665 | 0.1639 | 0.1652 | 0.1625 | 0.1637 | |
| 0.1645 | 0.1645 | 0.1650 | 0.1649 | 0.1650 | 0.1630 | 0.1493 | 0.1533 | 0.1474 | 0.1460 | |
| 0.1489 | 0.1499 | 0.1495 | 0.1491 | 0.1489 | 0.1503 | 0.1507 | 0.1505 | 0.1477 | 0.1496 | |
| X22 | 0.1517 | 0.1496 | 0.1504 | 0.1498 | 0.1528 | 0.1519 | 0.1534 | 0.1516 | 0.1555 | 0.1520 |
| 0.1512 | 0.1546 | 0.1538 | 0.1551 | 0.1563 | 0.1536 | 0.1543 | 0.1519 | 0.1514 | 0.1520 | |
| 0.1501 | 0.1514 | 0.1483 | 0.1499 | 0.1502 | 0.1550 | 0.1537 | 0.1507 | 0.1557 | 0.1537 | |
| 0.1556 | 0.1545 | 0.1529 | 0.1500 | 0.1380 | 0.1343 | 0.1346 | 0.1544 | 0.1458 | 0.1424 | |
| X23 | 0.1464 | 0.1460 | 0.1446 | 0.1448 | 0.1476 | 0.1464 | 0.1434 | 0.1432 | 0.1450 | 0.1420 |
| 0.1448 | 0.1452 | 0.1456 | 0.1462 | 0.1464 | 0.1464 | 0.1444 | 0.1440 | 0.1422 | 0.1442 | |
| 0.1470 | 0.1478 | 0.1468 | 0.1482 | 0.1472 | 0.1462 | 0.1478 | 0.1494 | 0.1488 | 0.1496 | |
| 0.1480 | 0.1476 | 0.1502 | 0.1496 | 0.1488 | 0.1488 | 0.1484 | 0.1534 | 0.1490 | 0.1486 | |
| X24 | 0.1466 | 0.1460 | 0.1438 | 0.1458 | 0.1488 | 0.1466 | 0.1494 | 0.1502 | 0.1486 | 0.1488 |
| 0.1512 | 0.1490 | 0.1470 | 0.1478 | 0.1484 | 0.1490 | 0.1474 | 0.1456 | 0.1464 | 0.1446 | |
| 0.3468 | 0.1484 | 0.1478 | 0.1486 | 0.1470 | 0.1448 | 0.1460 | 0.1458 | 0.1458 | 0.1456 | |
| 0.1452 | 0.1470 | 0.1470 | 0.1458 | 0.1450 | 0.1456 | 0.1462 | 0.1442 | 0.1464 | 0.1468 | |
| X25 | 0.1484 | 0.1474 | 0.1488 | 0.1460 | 0.1462 | 0.1464 | 0.1452 | 0.1450 | 0.1438 | 0.1434 |
| 0.1438 | 0.1438 | 0.1436 | 0.1436 | 0.1432 | 0.1412 | 0.1428 | 0.1418 | 0.1422 | 0.1422 | |
| 0.1432 | 0.1406 | 0.1420 | 0.1402 | 0.1410 | 0.1418 | 0.1432 | 0.1450 | 0.1418 | 0.1424 | |
| 0.1412 | 0.1408 | 0.1412 | 0.1390 | 0.1412 | 0.1398 | 0.1406 | 0.1394 | 0.1392 | 0.1382 | |
| X31 | 0.1221 | 0.1219 | 0.1207 | 0.1215 | 0.1222 | 0.1296 | 0.1235 | 0.1295 | 0.1280 | 0.1233 |
| 0.1218 | 0.1159 | 0.1163 | 0.1195 | 0.1190 | 0.1271 | 0.1247 | 0.1232 | 0.1233 | 0.1237 | |
| 0.1210 | 0.1227 | 0.1233 | 0.1222 | 0.1252 | 0.1230 | 0.1049 | 0.1033 | 0.0899 | 0.1003 | |
| 0.1044 | 0.1060 | 0.1064 | 0.1042 | 0.1072 | 0.1071 | 0.1070 | 0.1070 | 0.1041 | 0.1049 | |
| X32 | 0.1068 | 0.1063 | 0.1069 | 0.1057 | 0.1091 | 0.1061 | 0.1094 | 0.1067 | 0.1109 | 0.1111 |
| 0.1112 | 0.1096 | 0.1074 | 0.1085 | 0.1109 | 0.1116 | 0.1110 | 0.1113 | 0.1106 | 0.1110 | |
| 0.1091 | 0.1080 | 0.1044 | 0.1098 | 0.1084 | 0.1102 | 0.1078 | 0.1087 | 0.1111 | 0.1116 | |
| 0.1124 | 0.1128 | 0.1110 | 0.1078 | 0.1101 | 0.1115 | 0.1131 | 0.1108 | 0.1111 | 0.1079 | |
| X33 | 0.1105 | 0.1092 | 0.1074 | 0.1096 | 0.1055 | 0.1076 | 0.1003 | 0.1031 | 0.1040 | 0.1046 |
| 0.1041 | 0.1021 | 0.1041 | 0.1053 | 0.1057 | 0.1038 | 0.1029 | 0.1037 | 0.1012 | 0.0997 | |
| 0.1020 | 0.1020 | 0.0990 | 0.1049 | 0.1066 | 0.1065 | 0.1098 | 0.1102 | 0.1076 | 0.1116 | |
| 0.1097 | 0.1150 | 0.1120 | 0.1078 | 0.1106 | 0.1075 | 0.1061 | 0.1090 | 0.1098 | 0.1105 | |
| X34 | 0.1105 | 0.1081 | 0.1075 | 0.1059 | 0.1097 | 0.1105 | 0.1086 | 0.1085 | 0.1095 | 0.1084 |
| 0.1093 | 0.1113 | 0.1122 | 0.1139 | 0.1140 | 0.1129 | 0.1119 | 0.1107 | 0.1119 | 0.1137 | |
| 0.1128 | 0.1122 | 0.1104 | 0.1129 | 0.1130 | 0.1143 | 0.1132 | 0.1132 | 0.1115 | 0.1111 | |
| 0.1123 | 0.1124 | 0.1117 | 0.1120 | 0.1130 | 0.1127 | 0.1158 | 0.1145 | 0.1138 | 0.1144 | |
| X35 | 0.1160 | 0.1137 | 0.1159 | 0.1164 | 0.1158 | 0.1165 | 0.1167 | 0.1160 | 0.1155 | 0.1175 |
| 0.1170 | 0.1175 | 0.1168 | 0.1191 | 0.1190 | 0.1191 | 0.1190 | 0.1211 | 0.1196 | 0.1187 | |
| 0.1191 | 0.1202 | 0.1200 | 0.1205 | 0.1194 | 0.1193 | 0.1195 | 0.1180 | 0.1190 | 0.1194 | |
| 0.1197 | 0.1194 | 0.1173 | 0.1187 | 0.1169 | 0.1179 | 0.1184 | 0.1197 | 0.1194 | 0.1196 | |
| X41 | 4.4090 | 4.3780 | 4.3430 | 4.2950 | 4.2890 | 4.2890 | 4.2740 | 4.1840 | 4.1820 | 4.2020 |
| 4.2130 | 4.2240 | 4.2220 | 4.2250 | 4.2160 | 4.2220 | 4.2210 | 4.2410 | 4.2200 | 4.2180 | |
| 4.2260 | 4.2430 | 4.2390 | 4.2370 | 4.2270 | 4.2300 | 4.2210 | 4.2200 | 4.2430 | 4.6660 | |
| 4.4540 | 4.4370 | 4.4380 | 4.4410 | 4.4400 | 4.4350 | 4.4330 | 4.4430 | 4.4460 | 4.4420 | |
| X42 | 4.4480 | 4.4380 | 4.4420 | 4.4320 | 4.4270 | 4.4320 | 4.4220 | 4.4320 | 4.4240 | 4.4270 |
| 4.4590 | 4.4240 | 4.4650 | 4.4180 | 4.4200 | 4.4180 | 4.4190 | 4.4230 | 4.4200 | 4.4460 | |
| 4.4210 | 4.4040 | 4.4120 | 4.4000 | 4.4100 | 4.4150 | 4.4070 | 4.4120 | 4.3920 | 4.4020 | |
| 4.3930 | 4.3920 | 4.3860 | 4.3890 | 4.3820 | 4.3790 | 4.4120 | 4.3750 | 4.3740 | 4.3790 | |
| X43 | 4.3680 | 4.3840 | 4.3800 | 4.3690 | 4.3840 | 4.3830 | 4.3830 | 4.3820 | 4.3830 | 4.3850 |
| 4.3800 | 4.3800 | 4.3710 | 4.3720 | 4.3740 | 4.3890 | 4.3720 | 4.3670 | 4.3750 | 4.3650 | |
| 4.3600 | 4.3570 | 4.3640 | 4.3570 | 4.3550 | 0.3570 | 4.3480 | 4.3470 | 4.3470 | 4.3400 | |
| 4.3460 | 4.3360 | 4.3190 | 4.3300 | 4.3480 | 4.3500 | 4.3500 | 4.3460 | 4.3500 | 4.3500 | |
| X44 | 4.4000 | 4.3440 | 4.3410 | 4.3420 | 4.3510 | 4.3450 | 4.3370 | 4.3370 | 4.3340 | 4.3330 |
| 4.3330 | 4.3210 | 4.3250 | 4.3180 | 4.3300 | 4.3100 | 4.3190 | 4.3160 | 4.3160 | 4.3150 | |
| 4.3090 | 4.3040 | 4.3060 | 4.3050 | 4.3010 | 4.3000 | 4.2960 | 4.2940 | 4.2860 | 4.2860 | |
| 4.2890 | 4.2940 | 4.2900 | 4.3070 | 4.2890 | 4.2800 | 4.2820 | 4.2880 | 4.2810 | 4.2980 | |
| X45 | 4.3000 | 4.2930 | 4.2980 | 4.3303 | 4.2990 | 4.2870 | 4.3030 | 4.2910 | 4.2950 | 4.3050 |
| 4.3020 | 4.3120 | 4.3250 | 4.3090 | 4.3240 | 4.3210 | 4.3240 | 4.3230 | 4.3270 | 4.3290 | |
| 4.3230 | 4.3290 | 4.3290 | 4.3350 | 4.3210 | 4.3240 | 4.3270 | 4.4620 | 4.4120 | 4.3740 | |
| 4.3960 | 4.3730 | 4.3550 | 4.3540 | 4.3500 | 4.3430 | 4.3470 | 4.3550 | 4.3380 | 4.3310 | |
| Y11 | 0.1666 | 0.1666 | 0.1670 | 0.1696 | 0.1665 | 0.1671 | 0.1652 | 0.1663 | 0.1656 | 0.1656 |
| 0.1659 | 0.1655 | 0.1640 | 0.1634 | 0.1631 | 0.1618 | 0.1617 | 0.1615 | 0.1597 | 0.1592 | |
| 0.1584 | 0.1585 | 0.1575 | 0.1578 | 0.1573 | 0.1567 | 0.1834 | 0.1825 | 0.1827 | 0.1822 | |
| 0.1828 | 0.1817 | 0.1820 | 0.1823 | 0.1808 | 0.1818 | 0.1814 | 0.1816 | 0.1808 | 0.1807 | |
| Y12 | 0.1809 | 0.1794 | 0.1799 | 0.1799 | 0.1788 | 0.1795 | 0.1785 | 0.1785 | 0.1780 | 0.1777 |
| 0.1778 | 0.1777 | 0.1766 | 0.1767 | 0.1761 | 0.1770 | 0.1757 | 0.1765 | 0.1755 | 0.1755 | |
| 0.1746 | 0.1757 | 0.1741 | 0.1743 | 0.1741 | 0.1732 | 0.1736 | 0.1723 | 0.1730 | 0.1708 | |
| 0.1708 | 0.1702 | 0.1691 | 0.1686 | 0.1683 | 0.1676 | 0.1668 | 0.1670 | 0.1649 | 0.1644 | |
| Y13 | 0.1637 | 0.1639 | 0.1655 | 0.1641 | 0.1643 | 0.1641 | 0.1625 | 0.2038 | 0.2037 | 0.2033 |
| 0.2014 | 0.2028 | 0.2022 | 0.2026 | 0.2014 | 0.2013 | 0.2007 | 0.2012 | 0.1999 | 0.2012 | |
| 0.1998 | 0.1999 | 0.1988 | 0.1992 | 0.1988 | 0.1985 | 0.1977 | 0.1976 | 0.1979 | 0.1981 | |
| 0.1966 | 0.1973 | 0.1979 | 0.1984 | 0.1973 | 0.1969 | 0.1963 | 0.1960 | 0.1953 | 0.1941 | |
| Y14 | 0.1958 | 0.1952 | 0.1954 | 0.1938 | 0.1940 | 0.1956 | 0.1945 | 0.1937 | 0.1954 | 0.1947 |
| 0.1950 | 0.1955 | 0.1947 | 0.1956 | 0.1945 | 0.1932 | 0.1942 | 0.1925 | 0.1924 | 0.1934 | |
| 0.1904 | 0.1905 | 0.1909 | 0.1906 | 0.1989 | 0.1898 | 0.1891 | 0.1892 | 0.1886 | 0.1880 | |
| 0.1884 | 0.1890 | 0.1874 | 0.1872 | 0.1880 | 0.1855 | 0.1862 | 0.1866 | 0.1849 | 0.1841 | |
| Y15 | 0.1857 | 0.1844 | 0.1837 | 0.1831 | 0.1835 | 0.1826 | 0.1828 | 0.1834 | 0.1833 | 0.1837 |
| 0.1822 | 0.1829 | 0.1823 | 0.1807 | 0.1833 | 0.1835 | 0.1832 | 0.1828 | 0.1816 | 0.1820 | |
| 0.1805 | 0.1808 | 0.1803 | 0.1795 | 0.1785 | 0.1794 | 0.1795 | 0.1788 | 0.1786 | 0.1781 | |
| 0.1771 | 0.1775 | 0.1774 | 0.1769 | 0.1780 | 0.1778 | 0.1758 | 0.1740 | 0.1736 | 0.1738 | |
| Y21 | 0.3111 | 0.3124 | 0.3205 | 0.3268 | 0.3225 | 0.3268 | 0.3305 | 0.3245 | 0.3247 | 0.3245 |
| 0.3300 | 0.3279 | 0.3265 | 0.3221 | 0.3209 | 0.3227 | 0.3196 | 0.3150 | 0.3193 | 0.3182 | |
| 0.3148 | 0.3122 | 0.3133 | 0.3107 | 0.3131 | 0.3071 | 0.3412 | 0.3401 | 0.3357 | 0.3466 | |
| 0.3422 | 0.3390 | 0.3372 | 0.3364 | 0.3398 | 0.3392 | 0.3384 | 0.3383 | 0.3344 | 0.3394 | |
| Y22 | 0.3386 | 0.3342 | 0.3364 | 0.3338 | 0.3381 | 0.3388 | 0.3347 | 0.3348 | 0.3321 | 0.3367 |
| 0.3367 | 0.3322 | 0.3300 | 0.3309 | 0.3346 | 0.3341 | 0.3335 | 0.3303 | 0.3320 | 0.3317 | |
| 0.3295 | 0.3265 | 0.3299 | 0.3267 | 0.3271 | 0.3253 | 0.3297 | 0.3247 | 0.3243 | 0.3269 | |
| 0.3229 | 0.3211 | 0.3171 | 0.3202 | 0.3170 | 0.3125 | 0.3144 | 0.3165 | 0.3079 | 0.3087 | |
| Y23 | 0.3117 | 0.3095 | 0.3152 | 0.3222 | 0.3171 | 0.3169 | 0.3157 | 0.3480 | 0.3498 | 0.3469 |
| 0.3447 | 0.3476 | 0.3507 | 0.3470 | 0.3403 | 0.3359 | 0.3412 | 0.3399 | 0.3459 | 0.3449 | |
| 0.3479 | 0.3422 | 0.3446 | 0.3471 | 0.3467 | 0.3461 | 0.3421 | 0.3413 | 0.3416 | 0.3457 | |
| 0.3423 | 0.3439 | 0.3423 | 0.3465 | 0.3405 | 0.3399 | 0.3372 | 0.3387 | 0.3333 | 0.3349 | |
| Y24 | 0.3419 | 0.3436 | 0.3510 | 0.3392 | 0.3354 | 0.3350 | 0.3500 | 0.3354 | 0.3358 | 0.3349 |
| 0.3385 | 0.3414 | 0.3351 | 0.3394 | 0.3371 | 0.3374 | 0.3370 | 0.3365 | 0.3342 | 0.3389 | |
| 0.3386 | 0.3394 | 0.3374 | 0.3355 | 0.3357 | 0.3312 | 0.3274 | 0.3353 | 0.3351 | 0.3325 | |
| 0.3305 | 0.3314 | 0.3304 | 0.3238 | 0.3315 | 0.3259 | 0.3253 | 0.3308 | 0.3215 | 0.3233 | |
| Y25 | 0.3282 | 0.3208 | 0.3211 | 0.3138 | 0.3144 | 0.3199 | 0.3182 | 0.3196 | 0.3205 | 0.3180 |
| 0.3166 | 0.3170 | 0.3181 | 0.3139 | 0.3212 | 0.3254 | 0.3238 | 0.3193 | 0.3204 | 0.3168 | |
| 0.3148 | 0.3204 | 0.3146 | 0.3132 | 0.3191 | 0.3164 | 0.3141 | 0.3165 | 0.3137 | 0.3160 | |
| 0.3135 | 0.3137 | 0.3188 | 0.3177 | 0.3193 | 0.3239 | 0.3158 | 0.3236 | 0.3291 | 0.3262 | |
| Y31 | 0.2517 | 0.2634 | 0.2590 | 0.2808 | 0.2869 | 0.2827 | 0.2913 | 0.2909 | 0.2893 | 0.2903 |
| 0.2999 | 0.2961 | 0.2930 | 0.3040 | 0.2971 | 0.3125 | 0.2968 | 0.2979 | 0.2998 | 0.3003 | |
| 0.3023 | 0.2986 | 0.3008 | 0.3022 | 0.3017 | 0.3218 | 0.2338 | 0.2414 | 0.2510 | 0.2498 | |
| 0.2424 | 0.2451 | 0.2477 | 0.2473 | 0.2494 | 0.2523 | 0.2523 | 0.2496 | 0.2557 | 0.2591 | |
| Y32 | 0.2485 | 0.2534 | 0.2636 | 0.2670 | 0.2661 | 0.2641 | 0.2581 | 0.2637 | 0.2733 | 0.2735 |
| 0.2644 | 0.2622 | 0.2669 | 0.2713 | 0.2663 | 0.2720 | 0.2753 | 0.2758 | 0.2722 | 0.2755 | |
| 0.2710 | 0.2870 | 0.2820 | 0.2770 | 0.2727 | 0.2761 | 0.2812 | 0.2777 | 0.2880 | 0.2919 | |
| 0.2882 | 0.2784 | 0.2788 | 0.2792 | 0.2799 | 0.2731 | 0.2717 | 0.2851 | 0.2606 | 0.2696 | |
| Y33 | 0.2786 | 0.2774 | 0.2921 | 0.2991 | 0.2982 | 0.2974 | 0.2980 | 0.2015 | 0.1872 | 0.1865 |
| 0.2016 | 0.1980 | 0.1982 | 0.2022 | 0.2071 | 0.2020 | 0.1882 | 0.1877 | 0.2065 | 0.2057 | |
| 0.2052 | 0.2143 | 0.2135 | 0.2261 | 0.2110 | 0.2077 | 0.2089 | 0.2134 | 0.2161 | 0.2119 | |
| 0.2109 | 0.2130 | 0.2180 | 0.2096 | 0.2102 | 0.2152 | 0.2137 | 0.2110 | 0.2113 | 0.2126 | |
| Y34 | 0.2170 | 0.2130 | 0.2190 | 0.2192 | 0.2112 | 0.2214 | 0.2166 | 0.2137 | 0.2109 | 0.2024 |
| 0.2117 | 0.2102 | 0.2087 | 0.2050 | 0.2149 | 0.2134 | 0.2067 | 0.2140 | 0.2239 | 0.2153 | |
| 0.2144 | 0.2103 | 0.2145 | 0.2190 | 0.2250 | 0.2137 | 0.2060 | 0.2153 | 0.2132 | 0.2160 | |
| 0.2079 | 0.2047 | 0.2130 | 0.2058 | 0.2174 | 0.2138 | 0.2142 | 0.2138 | 0.2022 | 0.2169 | |
| Y35 | 0.2206 | 0.2133 | 0.2141 | 0.2031 | 0.2073 | 0.2099 | 0.2066 | 0.2052 | 0.2172 | 0.2131 |
| 0.2140 | 0.2184 | 0.2152 | 0.2099 | 0.2258 | 0.2264 | 0.2273 | 0.2322 | 0.2204 | 0.2248 | |
| 0.2242 | 0.2251 | 0.2222 | 0.2317 | 0.2193 | 0.2262 | 0.2255 | 0.2332 | 0.2299 | 0.2289 | |
| 0.2305 | 0.2398 | 0.2401 | 0.2306 | 0.2365 | 0.2398 | 0.2439 | 0.2595 | 0.2529 | 0.2557 | |
| Y41 | 5.3920 | 5.3260 | 5.3080 | 5.2620 | 5.2800 | 5.2460 | 5.1950 | 5.2280 | 5.1840 | 5.1820 |
| 5.1590 | 5.1310 | 5.0980 | 4.9840 | 5.0190 | 4.9340 | 4.9260 | 4.9500 | 4.9690 | 4.8960 | |
| 4.7990 | 4.8330 | 4.8220 | 4.7450 | 4.7840 | 4.8260 | 4.8960 | 4.8920 | 4.9120 | 4.8390 | |
| 4.8230 | 4.7960 | 4.8000 | 4.8180 | 4.8240 | 4.8310 | 4.8370 | 4.8720 | 4.8410 | 4.8410 | |
| Y42 | 4.8610 | 4.8220 | 4.6890 | 4.7250 | 4.7070 | 4.7300 | 4.6980 | 4.6810 | 4.6620 | 4.7610 |
| 4.7460 | 4.6870 | 4.7120 | 4.7080 | 4.6910 | 4.5130 | 4.4670 | 4.5120 | 4.5410 | 4.3910 | |
| 4.4220 | 4.5130 | 4.5950 | 4.5810 | 4.5420 | 4.5400 | 4.5160 | 4.5220 | 4.5180 | 4.5660 | |
| 4.5380 | 4.5450 | 4.4510 | 4.4570 | 4.4810 | 4.4860 | 4.4940 | 4.4690 | 4.4180 | 4.4170 | |
| Y43 | 4.3700 | 4.4000 | 4.3950 | 4.3840 | 4.3740 | 4.3800 | 4.3310 | 4.3230 | 4.3140 | 4.2870 |
| 4.2300 | 4.2440 | 4.2500 | 4.2200 | 4.2150 | 4.2540 | 4.2100 | 4.1980 | 4.2550 | 4.2210 | |
| 4.2110 | 4.2000 | 4.1810 | 4.1790 | 4.1840 | 4.1570 | 4.1440 | 4.1600 | 4.1150 | 4.0940 | |
| 4.1230 | 4.1280 | 5.2340 | 5.2320 | 5.2110 | 5.2210 | 5.2280 | 5.2060 | 5.1800 | 5.1890 | |
| Y44 | 5.1510 | 5.1240 | 5.1230 | 5.1220 | 5.0830 | 5.0600 | 5.0930 | 5.0750 | 5.0490 | 5.0520 |
| 5.0150 | 5.0250 | 5.0750 | 5.0150 | 4.9010 | 4.9300 | 4.9080 | 4.8860 | 4.8780 | 4.9040 | |
| 4.8980 | 4.8830 | 4.8510 | 4.8510 | 4.8370 | 4.9340 | 8.8960 | 4.8160 | 4.7640 | 4.7940 | |
| 4.8010 | 4.7670 | 4.7450 | 4.7540 | 4.7710 | 4.7560 | 4.7540 | 4.7360 | 4.6780 | 4.6650 | |
| Y45 | 4.6770 | 4.6610 | 4.6500 | 4.6280 | 4.6440 | 4.6320 | 4.6120 | 4.4620 | 4.6770 | 4.6580 |
| 4.6290 | 4.6220 | 4.6300 | 4.6140 | 4.6260 | 4.6130 | 4.5850 | 4.5690 | 4.5820 | 4.5500 | |
| 4.5330 | 4.5520 | 4.5040 | 4.4760 | 4.5660 | 4.5280 | 4.5550 | 4.5230 | 4.5190 | 4.5390 | |
| 4.5220 | 4.5210 | 4.5090 | 4.4870 | 4.5270 | 4.4730 | 4.4710 | 4.4900 | 4.4570 | 4.4510 | |
| Z11 | 0.3207 | 0.3213 | 0.3213 | 0.3235 | 0.3322 | 0.3419 | 0.3434 | 0.3440 | 0.3454 | 0.3461 |
| 0.3474 | 0.3476 | 0.3432 | 0.3468 | 0.3439 | 0.3423 | 0.3440 | 0.3430 | 0.3436 | 0.3420 | |
| 0.3416 | 0.3402 | 0.3373 | 0.3403 | 0.3414 | 0.3423 | 0.3420 | 0.3423 | 0.3425 | 0.3379 | |
| 0.3379 | 0.3391 | 0.3386 | 0.3355 | 0.3352 | 0.3361 | 0.3333 | 0.3333 | 0.3315 | 0.3347 | |
| Z12 | 0.3347 | 0.3320 | 0.3323 | 0.3327 | 0.3329 | 0.3287 | 0.3304 | 0.3312 | 0.3285 | 0.3287 |
| 0.3309 | 0.3270 | 0.3274 | 0.3285 | 0.3283 | 0.3305 | 0.3274 | 0.3261 | 0.3264 | 0.3251 | |
| 0.3271 | 0.3252 | 0.3275 | 0.3275 | 0.3287 | 0.3270 | 0.3269 | 0.3297 | 0.3266 | 0.3308 | |
| 0.3293 | 0.3304 | 0.3323 | 0.3305 | 0.3305 | 0.3330 | 0.3339 | 0.3342 | 0.3312 | 0.3315 | |
| Z13 | 0.3312 | 0.3301 | 0.3315 | 0.3307 | 0.3315 | 0.3320 | 0.3311 | 0.3327 | 0.3292 | 0.3301 |
| 0.3315 | 0.3289 | 0.3246 | 0.3267 | 0.3295 | 0.3270 | 0.3238 | 0.3264 | 0.3251 | 0.3264 | |
| 0.3260 | 0.3247 | 0.3224 | 0.3235 | 0.3249 | 0.3230 | 0.3232 | 0.3273 | 0.3249 | 0.3270 | |
| 0.3218 | 0.3244 | 0.3006 | 0.3030 | 0.3041 | 0.3174 | 0.3220 | 0.3196 | 0.3241 | 0.3251 | |
| Z14 | 0.3263 | 0.3266 | 0.3282 | 0.3270 | 0.3290 | 0.3198 | 0.3237 | 0.3229 | 0.3261 | 0.3238 |
| 0.3259 | 0.3221 | 0.3309 | 0.3271 | 0.3242 | 0.3235 | 0.3240 | 0.3261 | 0.3294 | 0.3287 | |
| 0.3267 | 0.3277 | 0.3263 | 0.3262 | 0.3278 | 0.3276 | 0.3271 | 0.3267 | 0.3289 | 0.3270 | |
| 0.3266 | 0.3299 | 0.3068 | 0.3148 | 0.3322 | 0.3323 | 0.3320 | 0.3336 | 0.3326 | 0.3322 | |
| Z15 | 0.3326 | 0.3317 | 0.3301 | 0.3316 | 0.3336 | 0.3280 | 0.3292 | 0.3297 | 0.3283 | 0.3283 |
| 0.3264 | 0.3279 | 0.3275 | 0.3294 | 0.3245 | 0.3268 | 0.3261 | 0.3262 | 0.3253 | 0.3272 | |
| 0.3270 | 0.3252 | 0.3284 | 0.3253 | 0.3265 | 0.3277 | 0.3291 | 0.3287 | 0.3256 | 0.3239 | |
| 0.3248 | 0.3261 | 0.3252 | 0.3249 | 0.3254 | 0.3290 | 0.3275 | 0.3274 | 0.3274 | 0.3251 | |
| Z21 | 0.2893 | 0.2863 | 0.2801 | 0.2847 | 0.3271 | 0.3448 | 0.3409 | 0.3346 | 0.3249 | 0.3425 |
| 0.3360 | 0.3368 | 0.3361 | 0.3411 | 0.3434 | 0.3459 | 0.3460 | 0.3481 | 0.3518 | 0.3495 | |
| 0.3478 | 0.3477 | 0.3506 | 0.3470 | 0.3470 | 0.3501 | 0.3477 | 0.3561 | 0.3489 | 0.3529 | |
| 0.3539 | 0.3544 | 0.3525 | 0.3515 | 0.3560 | 0.3596 | 0.3567 | 0.3616 | 0.3602 | 0.3589 | |
| Z22 | 0.3541 | 0.3561 | 0.3607 | 0.3636 | 0.3614 | 0.3595 | 0.3586 | 0.3575 | 0.3574 | 0.3563 |
| 0.3601 | 0.3619 | 0.3647 | 0.3599 | 0.3621 | 0.3647 | 0.3557 | 0.3457 | 0.3558 | 0.3509 | |
| 0.3525 | 0.3527 | 0.3484 | 0.3452 | 0.3474 | 0.3438 | 0.3500 | 0.3447 | 0.3429 | 0.3508 | |
| 0.3397 | 0.3375 | 0.3503 | 0.3421 | 0.3421 | 0.3362 | 0.3328 | 0.3409 | 0.3391 | 0.3364 | |
| Z23 | 0.3287 | 0.3323 | 0.3313 | 0.3416 | 0.3315 | 0.3352 | 0.3396 | 0.3349 | 0.3402 | 0.3406 |
| 0.3472 | 0.3526 | 0.3439 | 0.3462 | 0.3427 | 0.3492 | 0.3507 | 0.3550 | 0.3456 | 0.3522 | |
| 0.3480 | 0.3397 | 0.3474 | 0.3499 | 0.3503 | 0.3365 | 0.3450 | 0.3516 | 0.3506 | 0.3528 | |
| 0.3493 | 0.3546 | 0.2995 | 0.3094 | 0.2950 | 0.3479 | 0.3361 | 0.3394 | 0.3484 | 0.3441 | |
| Z24 | 0.3469 | 0.3380 | 0.3356 | 0.3378 | 0.3385 | 0.3338 | 0.3396 | 0.3345 | 0.3363 | 0.3426 |
| 0.3333 | 0.3298 | 0.3335 | 0.3339 | 0.3397 | 0.3349 | 0.3357 | 0.3361 | 0.3401 | 0.3382 | |
| 0.3379 | 0.3356 | 0.3309 | 0.3333 | 0.3328 | 0.3330 | 0.3412 | 0.3334 | 0.3264 | 0.3297 | |
| 0.3302 | 0.3318 | 0.2961 | 0.3143 | 0.3616 | 0.3506 | 0.3463 | 0.3446 | 0.3412 | 0.3393 | |
| Z25 | 0.3454 | 0.3396 | 0.3453 | 0.3455 | 0.3517 | 0.3426 | 0.3590 | 0.3516 | 0.3481 | 0.3502 |
| 0.3440 | 0.3428 | 0.3455 | 0.3404 | 0.3518 | 0.3517 | 0.3389 | 0.3481 | 0.3382 | 0.3530 | |
| 0.3471 | 0.3566 | 0.3554 | 0.3539 | 0.3576 | 0.3536 | 0.3480 | 0.3568 | 0.3567 | 0.3524 | |
| 0.3587 | 0.3578 | 0.3535 | 0.3602 | 0.3565 | 0.3490 | 0.3532 | 0.3541 | 0.3507 | 0.3467 | |
| Z31 | 0.1810 | 0.1864 | 0.1803 | 0.1829 | 0.1605 | 0.1441 | 0.1436 | 0.1412 | 0.1414 | 0.1476 |
| 0.1502 | 0.1477 | 0.1507 | 0.1469 | 0.1490 | 0.1512 | 0.1461 | 0.1497 | 0.1511 | 0.1488 | |
| 0.1486 | 0.1480 | 0.1493 | 0.1451 | 0.1520 | 0.1537 | 0.1498 | 0.1478 | 0.1471 | 0.1496 | |
| 0.1467 | 0.1443 | 0.1446 | 0.1420 | 0.1454 | 0.1365 | 0.1347 | 0.1373 | 0.1380 | 0.1446 | |
| Z32 | 0.1434 | 0.1380 | 0.1413 | 0.1412 | 0.1452 | 0.1444 | 0.1396 | 0.1364 | 0.1400 | 0.1424 |
| 0.1408 | 0.1419 | 0.1415 | 0.1393 | 0.1472 | 0.1452 | 0.1387 | 0.1383 | 0.1267 | 0.1326 | |
| 0.1326 | 0.1398 | 0.1283 | 0.1291 | 0.1296 | 0.1282 | 0.1314 | 0.1235 | 0.1283 | 0.1179 | |
| 0.1206 | 0.1285 | 0.1365 | 0.1290 | 0.1290 | 0.1345 | 0.1191 | 0.1275 | 0.1290 | 0.1187 | |
| Z33 | 0.1252 | 0.1210 | 0.1268 | 0.1339 | 0.1333 | 0.1359 | 0.1309 | 0.1362 | 0.1315 | 0.1399 |
| 0.1387 | 0.1369 | 0.1326 | 0.1381 | 0.1308 | 0.1301 | 0.1322 | 0.1302 | 0.1260 | 0.1241 | |
| 0.1266 | 0.1210 | 0.1298 | 0.1264 | 0.1232 | 0.1250 | 0.1313 | 0.1284 | 0.1257 | 0.1281 | |
| 0.1321 | 0.1350 | 0.1665 | 0.1695 | 0.1692 | 0.1386 | 0.1352 | 0.1422 | 0.1409 | 0.1332 | |
| Z34 | 0.1387 | 0.1343 | 0.1349 | 0.1335 | 0.1289 | 0.1300 | 0.1282 | 0.1263 | 0.1258 | 0.1331 |
| 0.1268 | 0.1291 | 0.1353 | 0.1295 | 0.1304 | 0.1279 | 0.1345 | 0.1329 | 0.1329 | 0.1294 | |
| 0.1398 | 0.1386 | 0.1318 | 0.1278 | 0.1371 | 0.1317 | 0.1357 | 0.1361 | 0.1370 | 0.1416 | |
| 0.1291 | 0.1350 | 0.1368 | 0.1535 | 0.1340 | 0.1304 | 0.1312 | 0.1331 | 0.1276 | 0.1302 | |
| Z35 | 0.1232 | 0.1340 | 0.1316 | 0.1299 | 0.1375 | 0.1238 | 0.1344 | 0.1229 | 0.1331 | 0.1324 |
| 0.1297 | 0.1297 | 0.1233 | 0.1286 | 0.1314 | 0.1334 | 0.1259 | 0.1362 | 0.1151 | 0.1279 | |
| 0.1256 | 0.1287 | 0.1323 | 0.1216 | 0.1263 | 0.1296 | 0.1241 | 0.1274 | 0.1252 | 0.1310 | |
| 0.1276 | 0.1314 | 0.1328 | 0.1284 | 0.1284 | 0.1339 | 0.1346 | 0.1360 | 0.1356 | 0.1359 | |
| Z41 | 9.7920 | 9.8090 | 9.8090 | 9.8130 | 9.8190 | 9.8730 | 9.7850 | 9.8220 | 9.7880 | 9.7530 |
| 9.8170 | 9.7530 | 9.7060 | 9.7480 | 9.7840 | 9.7210 | 9.7330 | 9.7910 | 9.9090 | 9.9510 | |
| 9.9670 | 9.9340 | 9.8760 | 9.9070 | 9.9470 | 9.8780 | 9.9150 | 9.9200 | 9.9090 | 9.9220 | |
| 9.8440 | 9.8740 | 9.8000 | 9.8700 | 9.8970 | 9.8670 | 9.8760 | 9.8830 | 9.9370 | 9.9330 | |
| Z42 | 9.9070 | 9.8530 | 9.8510 | 9.8690 | 9.8250 | 9.8630 | 9.8610 | 9.8440 | 9.8500 | 9.7980 |
| 9.8300 | 9.8250 | 9.8370 | 9.8890 | 9.8350 | 9.8030 | 9.7550 | 9.7960 | 9.7760 | 9.7730 | |
| 9.7270 | 9.6260 | 9.6430 | 9.6620 | 9.6920 | 9.6800 | 9.6990 | 9.3850 | 9.7020 | 9.7160 | |
| 9.7420 | 9.6530 | 9.7390 | 9.7830 | 9.7030 | 9.7460 | 9.7360 | 9.8000 | 9.7490 | 9.7840 | |
| Z43 | 9.7060 | 9.7540 | 9.7830 | 9.7500 | 9.7290 | 9.7900 | 9.7790 | 9.7370 | 9.7640 | 9.6970 |
| 9.6850 | 9.7260 | 9.6830 | 9.6880 | 9.7230 | 9.7360 | 9.6930 | 9.7560 | 9.7500 | 9.7880 | |
| 9.7050 | 9.7660 | 9.7710 | 9.8240 | 9.8610 | 9.8290 | 9.8020 | 9.8550 | 9.7600 | 9.8230 | |
| 9.8610 | 9.8200 | 9.8420 | 9.8370 | 9.8340 | 9.8750 | 9.9040 | 9.8570 | 9.8000 | 9.8650 | |
| Z44 | 9.8190 | 9.8400 | 9.8350 | 9.7756 | 9.8520 | 9.8900 | 9.9230 | 9.8810 | 9.9580 | 9.9290 |
| 9.9320 | 9.6500 | 9.9680 | 9.9220 | 9.8580 | 9.9460 | 9.8760 | 9.9400 | 9.8370 | 9.7400 | |
| 9.8990 | 9.9440 | 9.9570 | 10.0360 | 9.8960 | 9.9550 | 10.0230 | 10.0170 | 9.9950 | 9.7420 | |
| 9.6220 | 9.7320 | 9.7280 | 9.9780 | 10.1120 | 10.0350 | 9.9930 | 9.6710 | 9.5720 | 9.6780 | |
| Z45 | 9.7530 | 9.7570 | 9.7510 | 9.8330 | 9.7730 | 9.7980 | 9.8460 | 9.8440 | 9.8750 | 9.8690 |
| 9.8300 | 9.6950 | 9.6930 | 9.6990 | 9.6540 | 9.6880 | 9.5790 | 9.6610 | 9.9250 | 9.8580 | |
| 9.6240 | 9.6830 | 9.8540 | 9.6300 | 9.5890 | 9.6450 | 9.7990 | 9.8260 | 9.9420 | 9.9150 | |
| 9.9150 | 9.7980 | 9.9240 | 9.8970 | 9.8820 | 9.8090 | 9.7990 | 9.8150 | 9.8580 | 9.8380 | |
References
- Hall, D.L.; Llinas, J. An introduction to multisensor data fusion. IEEE Proc. 1997, 85, 6–23. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W.; Zhang, J. Zero-sum matrix game with payoffs of Dempster–Shafer belief structures and its applications on sensors. Sensors 2017, 17, 922. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Du, J.; Bao, J. Maneuvering target tracking by adaptive statistics model. J. China Univ. Posts Telecommun. 2013, 20, 108–114. [Google Scholar] [CrossRef]
- Sun, S.; Tian, T.; Lin, H. Optimal Linear Estimators for Systems with Finite-Step Correlated Noises and Packet Dropout Compensations. IEEE Trans. Signal Process. 2016, 64, 5672–5681. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B.; Zhan, J.; Xie, C.; Zhou, D. A visibility graph power averaging aggregation operator: A methodology based on network analysis. Comput. Ind. Eng. 2016, 101, 260–268. [Google Scholar] [CrossRef]
- Sun, S.; Wang, G. Modeling and estimation for networked systems with multiple random transmission delays and packet losses. Syst. Control Lett. 2014, 73, 6–16. [Google Scholar] [CrossRef]
- Zhang, X.; Deng, Y.; Chan, F.T.S.; Adamatzky, A.; Mahadevan, S. Supplier selection based on evidence theory and analytic network process. Proc. Inst. Mech. Eng Part B J. Eng. Manuf. 2016, 230, 562–573. [Google Scholar] [CrossRef]
- Yang, F.; Ji, L.E.; Liu, S.; Feng, P. A fast and high accuracy registration method for multi-source images. Optik 2015, 126, 3061–3065. [Google Scholar] [CrossRef]
- Wu, F.; Wei, H.; Wang, X. Correction of image radial distortion based on division model. Opt. Eng. 2017, 56, 013108. [Google Scholar] [CrossRef]
- Yang, F.; Wei, H. Fusion of infrared polarization and intensity images using support value transform and fuzzy combination rules. Infrared Phys. Technol. 2013, 60, 235–243. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Luo, Y.; Tang, Y. Ranking Z-numbers with an improved ranking method for generalized fuzzy numbers. J. Intell. Fuzzy Syst. 2017, 32, 1931–1943. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, B.; Wang, X.; Jin, X.; Xu, J.; Su, T.; Wang, Z. A novel group decision-making method based on sensor data and fuzzy information. Sensors 2016, 16, 1799. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Zhou, D.; Jiang, W. A new fuzzy-evidential controller for stabilization of the planar inverted pendulum system. PLoS ONE 2016, 11, e0160416. [Google Scholar] [CrossRef] [PubMed]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multi-valued Mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 24. [Google Scholar]
- Zadeh, L. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Possibility Theory: An Approach to Computerized Processing of Uncertainty, Softcover Reprint of the Original, 1st ed.; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Dubois, D.; Prade, H. Fuzzy sets and probability: Misunderstandings, bridges and gaps. In Proceedings of the 2nd IEEE International Conference on Fuzzy Systems, San Francisco, CA, USA, 28 March–1 April 1993; Volume 2, pp. 1059–1068. [Google Scholar]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Dubois, D.; Prade, H. Possibility theory in information fusion. In Proceedings of the Third International Conference on Information Fusion, Paris, France, 10–13 July 2000; Volume 1, pp. PS6–PS19. [Google Scholar]
- Jiang, W.; Zhan, J. A modified combination rule in generalized evidence theory. Appl. Intell. 2017, 46, 630–640. [Google Scholar] [CrossRef]
- Song, M.; Jiang, W.; Xie, C.; Zhou, D. A new interval numbers power average operator in multiple attribute decision making. Int. J. Intell. Syst. 2017, 32, 631–644. [Google Scholar] [CrossRef]
- Zadeh, L.A. A simple view of the Dempster–Shafer theory of evidence and its implication for the rule of combination. AI Mag. 1986, 7, 85–90. [Google Scholar]
- Wang, J.; Xiao, F.; Deng, X.; Fei, L.; Deng, Y. Weighted evidence combination based on distance of evidence and entropy function. Int. J. Distrib. Sens. Netw. 2016, 12, 3218784. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, S.; Liu, X.; Zheng, H.; Wei, B. Evidence conflict measure based on OWA operator in open world. PLoS ONE 2017, 12, e0177828. [Google Scholar] [CrossRef] [PubMed]
- Mo, H.; Lu, X.; Deng, Y. A generalized evidence distance. J. Syst. Eng. Electron. 2016, 27, 470–476. [Google Scholar] [CrossRef]
- Martin, A.; Jousselme, A.L.; Osswald, C. Conflict measure for the discounting operation on belief functions. In Proceedings of the 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–8. [Google Scholar]
- Smarandache, F.; Han, D.; Martin, A. Comparative study of contradiction measures in the theory of belief functions. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 271–277. [Google Scholar]
- Martin, A. About conflict in the theory of belief functions. In Belief Functions: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 161–168. [Google Scholar]
- Deng, X.; Han, D.; Dezert, J.; Deng, Y.; Shyr, Y. Evidence combination from an evolutionary game theory perspective. IEEE Trans. Cybern. 2016, 46, 2070–2082. [Google Scholar] [CrossRef] [PubMed]
- Denoeux, T. A neural network classifier based on Dempster–Shafer theory. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2000, 30, 131–150. [Google Scholar] [CrossRef]
- Xiaobin, X.; Haishan, F.; Zhi, W.; Chenglin, W. An information fusion method of fault diagnosis based on interval basic probability assignment. Chin. J. Electron. 2011, 20, 255–260. [Google Scholar]
- Tabassian, M.; Ghaderi, R.; Ebrahimpour, R. Combination of multiple diverse classifiers using belief functions for handling data with imperfect labels. Expert Syst. Appl. 2012, 39, 1698–1707. [Google Scholar] [CrossRef]
- Baudrit, C.; Dubois, D. Practical representations of incomplete probabilistic knowledge. Comput. Stat. Data Anal. 2006, 51, 86–108. [Google Scholar] [CrossRef]
- Mönks, U.; Dörksen, H.; Lohweg, V.; Hübner, M. Information fusion of conflicting input data. Sensors 2016, 16, 1798. [Google Scholar] [CrossRef] [PubMed]
- Mönks, U. Information Fusion under Consideration of Conflicting Input Signals; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zhang, X.; Mahadevan, S.; Deng, X. Reliability analysis with linguistic data: An evidential network approach. Reliab. Eng. Syst. Saf. 2017, 162, 111–121. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Zhuang, M.; Shou, Y.; Tang, Y. Sensor Data Fusion with Z-Numbers and Its Application in Fault Diagnosis. Sensors 2016, 16, 1509. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Shi, W.; Deng, Y. Evaluating sensor reliability in classification problems based on evidence theory. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2006, 36, 970–981. [Google Scholar] [CrossRef]
- Yuan, K.; Xiao, F.; Fei, L.; Kang, B.; Deng, Y. Modeling sensor reliability in fault diagnosis based on evidence theory. Sensors 2016, 16, 113. [Google Scholar] [CrossRef] [PubMed]
- Glock, S.; Voth, K.; Schaede, J.; Lohweg, V. A framework for fossibilistic multi-source data fusion with monitoring of sensor reliability. In Proceedings of the World Conference on Soft Computing, San Francisco, CA, USA, 23–26 May 2011. [Google Scholar]
- Ehlenbröker, J.F.; Mönks, U.; Lohweg, V. Sensor defect detection in multisensor information fusion. J. Sens. Sens. Syst. 2016, 5, 337–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. A Note on Z-numbers. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Deng, X.; Xiao, F.; Deng, Y. An improved distance-based total uncertainty measure in belief function theory. Appl. Intell. 2017, 46, 898–915. [Google Scholar] [CrossRef]
- Fu, C.; Yang, J.; Yang, S. A group evidential reasoning approach based on expert reliability. Eur. J. Oper. Res. 2015, 246, 886–893. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Zhuang, M.; Tang, Y. Failure mode and effects analysis based on a novel fuzzy evidential method. Appl. Soft Comput. 2017, 57, 672–683. [Google Scholar] [CrossRef]
- Smets, P.; Kennes, R. The transferable belief model. Artif. Intell. 1994, 66, 191–234. [Google Scholar] [CrossRef]
- Jiang, W.; Zhuang, M.; Xie, C.; Wu, J. Sensing attribute weights: A novel basic belief assignment method. Sensors 2017, 17, 721. [Google Scholar] [CrossRef] [PubMed]
- Casella, G.; Berger, R. Statistical Inference; Duxbury Press: Pacific Grove, CA, USA, 2001. [Google Scholar]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Wen, C.; Xu, X. Theories and Applications in Multi-Source Uncertain Information Fusion—Fault Diagnosis and Reliability Evaluation; Beijing Science Press: Beijing, China, 2012. [Google Scholar]







| Methods | Classes | Overall Average | ||
|---|---|---|---|---|
| Not considering reliability | 99.00% | 95.50% | 100% | 98.17% |
| Support vector machine | 94.15% | 92.86% | 100% | 95.67% |
| Decision tree | 99.05% | 98.68% | 99.78% | 99.17% |
| Naive Bayesian | 98.05% | 96.94% | 100% | 98.33% |
| The proposed method | 100% | 100% | 100% | 100% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Zhuang, M.; Xie, C. A Reliability-Based Method to Sensor Data Fusion. Sensors 2017, 17, 1575. https://doi.org/10.3390/s17071575
Jiang W, Zhuang M, Xie C. A Reliability-Based Method to Sensor Data Fusion. Sensors. 2017; 17(7):1575. https://doi.org/10.3390/s17071575
Chicago/Turabian StyleJiang, Wen, Miaoyan Zhuang, and Chunhe Xie. 2017. "A Reliability-Based Method to Sensor Data Fusion" Sensors 17, no. 7: 1575. https://doi.org/10.3390/s17071575
APA StyleJiang, W., Zhuang, M., & Xie, C. (2017). A Reliability-Based Method to Sensor Data Fusion. Sensors, 17(7), 1575. https://doi.org/10.3390/s17071575