Indoor Positioning Algorithm Based on the Improved RSSI Distance Model
Abstract
:1. Introduction
- A RSSI Real-time Correction algorithm is proposed. A Bluetooth gateway is set at a fixed location and collects the RSSI of surrounding Bluetooth beacons to the server in real-time. Since the distance to the beacons is fixed, the server is able to estimate the fluctuation and feeds back to the user (mobile terminal) to correct the RSSI in real-time. Furthermore, the Kalman filtering is used to further smooth the RSSI.
- A back propagation neural network optimized by particle swarm optimization (PSO-BPNN) RSSI distance model is built. Then, the distance between the blind node and the anchor node is estimated using the RSSI distance model trained by PSO-BPNN.
- We perform an extensive experiment and the results show that the positioning error caused by the power fluctuation of the Bluetooth system is reduced obviously. The method does not need to spend a lot of time building a fingerprint database, and hence, it has low complexity. The experimental results show that the method has good localization accuracy and stability.
2. Related Work
2.1. RSSI Error Distribution
2.2. RSSI Distance Model
3. RSSI Real-Time Correction Algorithm
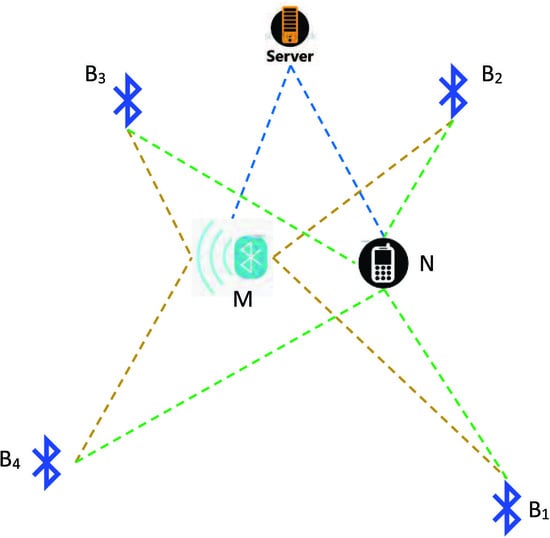
4. System Model
4.1. Positioning Step
- Deploy anchor nodes and Bluetooth gateways;
- The Bluetooth gateway measures the real-time signal strength of each anchor node and uploads it to the server;
- The server records the mean signal strength of each anchor node and calculates ;
- The blind node measures the signal strength of each anchor node, reads the server information, and corrects the RSSI according to (9);
- The corrected RSSI is smoothed by the Kalman filter and RSSI to is converted to distance using the PSO-BPNN model (15);
- The blind node position is estimated using the least squares algorithm.
4.2. PSO-BPNN RSSI Distance Model
| Algorithm 1 PSO-BPNN algorithm |
|
4.3. Kalman Filter
4.4. Least Squares Algorithm
5. Experiment
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent Advances in Indoor Localization: A Survey on Theoretical Approaches and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1327–1346. [Google Scholar] [CrossRef] [Green Version]
- Davidson, P.; Piché, R. A Survey of Selected Indoor Positioning Methods for Smartphones. IEEE Commun. Surv. Tutor. 2017, 19, 1347–1370. [Google Scholar] [CrossRef]
- Ren, A.; Zhou, F.; Rahman, A.; Wang, X.; Zhao, N.; Yang, X. A study of indoor positioning based on UWB base-station configurations. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 1939–1943. [Google Scholar]
- Saab, S.S.; Nakad, Z.S. A Standalone RFID Indoor Positioning System Using Passive Tags. IEEE Trans. Ind. Electron. 2011, 58, 1961–1970. [Google Scholar] [CrossRef]
- Wu, C.; Mu, Q.; Zhang, Z.; Jin, Y.; Wang, Z.; Shi, G. Indoor positioning system based on inertial MEMS sensors: Design and realization. In Proceedings of the 2016 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Chengdu, China, 19–22 June 2016; pp. 370–375. [Google Scholar]
- Tian, Y.; Shigaki, D.; Wang, W.; Ahn, C.J. A weighted least-squares method using received signal strength measurements for WLAN indoor positioning system. In Proceedings of the 2017 20th International Symposium on Wireless Personal Multimedia Communications (WPMC), Bali, Indonesia, 17–20 December 2017; pp. 310–314. [Google Scholar]
- Kim, J.; Jun, H. Vision-based location positioning using augmented reality for indoor navigation. IEEE Trans. Consum. Electron. 2008, 54, 954–962. [Google Scholar] [CrossRef]
- Pasku, V.; Angelis, A.D.; Dionigi, M.; Angelis, G.D.; Moschitta, A.; Carbone, P. A Positioning System Based on Low-Frequency Magnetic Fields. IEEE Trans. Ind. Electron. 2016, 63, 2457–2468. [Google Scholar] [CrossRef]
- Qi, J.; Liu, G.P. A Robust High-Accuracy Ultrasound Indoor Positioning System Based on a Wireless Sensor Network. Sensors 2017, 17, 2554. [Google Scholar] [CrossRef] [PubMed]
- Raharijaona, T.; Mawonou, R.; Nguyen, T.V.; Colonnier, F.; Boyron, M.; Diperi, J.; Viollet, S. Local Positioning System Using Flickering Infrared LEDs. Sensors 2017, 17, 2518. [Google Scholar] [CrossRef] [PubMed]
- Neburka, J.; Tlamsa, Z.; Benes, V.; Polak, L.; Kaller, O.; Bolecek, L.; Sebesta, J.; Kratochvil, T. Study of the performance of RSSI based Bluetooth Smart indoor positioning. In Proceedings of the 2016 26th International Conference Radioelektronika (RADIOELEKTRONIKA), Kosice, Slovakia, 19–20 April 2016; pp. 121–125. [Google Scholar]
- Wang, Y.; Yang, X.; Zhao, Y.; Liu, Y.; Cuthbert, L. Bluetooth positioning using RSSI and triangulation methods. In Proceedings of the 2013 IEEE 10th Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2013; pp. 837–842. [Google Scholar]
- Kotanen, A.; Hannikainen, M.; Leppakoski, H.; Hamalainen, T.D. Experiments on local positioning with Bluetooth. In Proceedings of the 2003 International Conference on Information Technology: Coding and Computing, Las Vegas, NV, USA, 28–30 April 2003; pp. 297–303. [Google Scholar] [Green Version]
- Shi, X.W.; Zhang, H.Q. Research on indoor location technology based on back propagation neural network and Taylor series. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 1886–1890. [Google Scholar]
- Zhou, C.; Yuan, J.; Liu, H.; Qiu, J. Bluetooth Indoor Positioning Based on RSSI and Kalman Filter. Wirel. Pers. Commun. 2017, 96, 4115–4130. [Google Scholar] [CrossRef]
- Dai, H.; Liu, H.B.; Xing, X.S.; Jin, Y. Indoor Positioning Algorithm Based on Parallel Multilayer Neural Network. In Proceedings of the 2016 International Conference on Information System and Artificial Intelligence (ISAI), Hong Kong, China, 24–26 June 2016; pp. 356–360. [Google Scholar]
- Wang, B.; Zhou, S.; Yang, L.T.; Mo, Y. Indoor positioning via subarea fingerprinting and surface fitting with received signal strength. Pervasive Mob. Comput. 2015, 23, 43–58. [Google Scholar] [CrossRef]
- Pelant, J.; Tlamsa, Z.; Benes, V.; Polak, L.; Kaller, O.; Bolecek, L.; Kufa, J.; Sebesta, J.; Kratochvil, T. BLE device indoor localization based on RSS fingerprinting mapped by propagation modes. In Proceedings of the 2017 27th International Conference Radioelektronika (RADIOELEKTRONIKA), Brno, Czech Republic, 19–20 April 2017; pp. 1–5. [Google Scholar]
- Liu, R.; Yuen, C.; Do, T.N.; Jiang, Y.; Liu, X.; Tan, U.X. Indoor positioning using similarity-based sequence and dead reckoning without training. In Proceedings of the IEEE International Workshop on Signal Processing Advances in Wireless Communications, Hokkaido, Japan, 3–6 July 2017; pp. 1–5. [Google Scholar]
- Zhou, M.; Tang, Y.; Tian, Z.; Geng, X. Semi-Supervised Learning for Indoor Hybrid Fingerprint Database Calibration With Low Effort. IEEE Access 2017, 5, 4388–4400. [Google Scholar] [CrossRef]
- Wang, B.; Chen, Q.; Yang, L.T.; Chao, H.C. Indoor smartphone localization via fingerprint crowdsourcing: Challenges and approaches. IEEE Wirel. Commun. 2016, 23, 82–89. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, B. RMapCS: Radio Map Construction From Crowdsourced Samples for Indoor Localization. IEEE Access 2018, 6, 24224–24238. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, Q.; Wang, Y.; Tian, Z. Hotspot Ranking Based Indoor Mapping and Mobility Analysis Using Crowdsourced Wi-Fi Signal. IEEE Access 2017, 5, 3594–3602. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, S.; Liu, W.; Mo, Y. Indoor Localization Based on Curve Fitting and Location Search Using Received Signal Strength. IEEE Trans. Ind. Electron. 2015, 62, 572–582. [Google Scholar] [CrossRef]
- Rozum, S.; Sebesta, J. SIMO RSS measurement in Bluetooth low power indoor positioning system. In Proceedings of the 2018 28th International Conference Radioelektronika (RADIOELEKTRONIKA), Prague, Czech Republic, 19–20 April 2018; pp. 1–5. [Google Scholar]
- Botta, M.; Simek, M. Adaptive Distance Estimation Based on RSSI in 802.15.4 Network. Radioengineering 2013, 22, 1162–1168. [Google Scholar]
- Yaoyi, L.I.; Xiaoxing, H.E.; Liu, S. Wireless Localization Algorithm Based on Path Loss Model Parameter Estimated in Real-Time. Chin. J. Sens. Actuators 2010, 23, 1328–1333. [Google Scholar]
- Röbesaat, J.; Zhang, P.; Abdelaal, M.; Theel, O. An Improved BLE Indoor Localization with Kalman-Based Fusion: An Experimental Study. Sensors 2017, 17, 951. [Google Scholar] [CrossRef] [PubMed]
- Jung, K.; Bermudez, P.B.V.; Hwang, H.; Oh, Y.; Kwak, J. Passenger’s location estimation using Kalman filter for Beacon fare collection in a wireless low floor tram. In Proceedings of the 2018 International Conference on Electronics, Information, and Communication (ICEIC), Honolulu, HI, USA, 24–27 January 2018; pp. 1–4. [Google Scholar]
- Houssaini, Z.S.; Zaimi, I.; Drissi, M.; Oumsis, M.; Ouatik, S.E.A. Trade-off between accuracy, cost, and QoS using a beacon-on-demand strategy and Kalman filtering over a VANET. Dig. Commun. Netw. 2018, 4, 13–26. [Google Scholar] [CrossRef]
- Fariz, N.; Jamil, N.; Din, M.M. An Improved Indoor Location Technique Using Kalman Filtering on RSSI. J. Comput. Theor. Nanosci. 2018, 24, 1591–1598. [Google Scholar] [CrossRef]
- Golestani, A.; Petreska, N.; Wilfert, D.; Zimmer, C. Improving the precision of RSSI-based low-energy localization using path loss exponent estimation. In Proceedings of the 2014 11th Workshop on Positioning, Navigation and Communication (WPNC), Dresden, Germany, 12–13 March 2014; pp. 1–6. [Google Scholar]
- Nowak, T.; Hartmann, M.; Zech, T.; Thielecke, J. A path loss and fading model for RSSI-based localization in forested areas. In Proceedings of the 2016 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Cairns, Australia, 19–23 September 2016; pp. 110–113. [Google Scholar]
- Nguyen, H.A.; Guo, H.; Low, K.S. Real-Time Estimation of Sensor Node’s Position Using Particle Swarm Optimization With Log-Barrier Constraint. IEEE Trans. Instrum. Meas. 2011, 60, 3619–3628. [Google Scholar] [CrossRef]
- Haider, S.S.; Zeng, X.J. Simplified Neural Networks Algorithms for Function Approximation and Regression Boosting on Discrete Input Spaces. Ph.D. Thesis, University of Manchester, Hong Kong, China, 2011. [Google Scholar]
- Lian, T.; Xie, M.; Xu, J.; Chen, L.; Gao, H. Modified BP neural network model is used for oddeven discrimination of integer number. Appl. Mech. Mater. 2013, 423–426, 2675–2678. [Google Scholar]
- Ren, J.; Yang, S. An Improved PSO-BP Network Model. In Proceedings of the Third International Symposium on Information Science and Engineering, Shanghai, China, 24–26 December 2010; pp. 426–429. [Google Scholar]
- Cao, J.; Cui, H.; Hao, S.; Jiao, L. Big Data: A Parallel Particle Swarm Optimization-Back-Propagation Neural Network Algorithm Based on MapReduce. PLoS ONE 2016, 11, e0157551. [Google Scholar] [CrossRef] [PubMed]












© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Geng, E.; Ye, Z.; Xu, Y.; Lin, J.; Pang, Y. Indoor Positioning Algorithm Based on the Improved RSSI Distance Model. Sensors 2018, 18, 2820. https://doi.org/10.3390/s18092820
Li G, Geng E, Ye Z, Xu Y, Lin J, Pang Y. Indoor Positioning Algorithm Based on the Improved RSSI Distance Model. Sensors. 2018; 18(9):2820. https://doi.org/10.3390/s18092820
Chicago/Turabian StyleLi, Guoquan, Enxu Geng, Zhouyang Ye, Yongjun Xu, Jinzhao Lin, and Yu Pang. 2018. "Indoor Positioning Algorithm Based on the Improved RSSI Distance Model" Sensors 18, no. 9: 2820. https://doi.org/10.3390/s18092820
APA StyleLi, G., Geng, E., Ye, Z., Xu, Y., Lin, J., & Pang, Y. (2018). Indoor Positioning Algorithm Based on the Improved RSSI Distance Model. Sensors, 18(9), 2820. https://doi.org/10.3390/s18092820