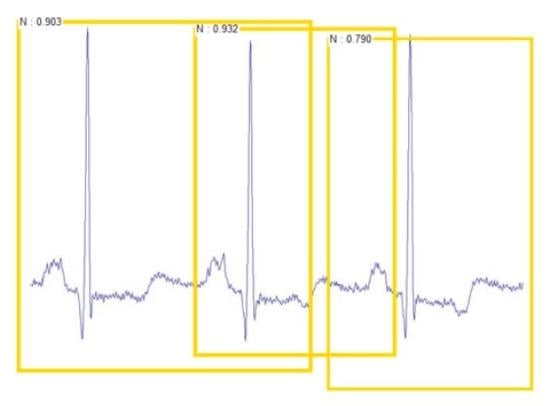
1. Introduction
An electrocardiogram (ECG) as a cardiac activity record provides important information about the state of the heart [
1]. ECG arrhythmia detection is necessary for early diagnosis of heart disease patients. On the one hand, it is very difficult for a doctor to analyze an electrocardiogram with a long recording time for a limited time. On the other hand, people are also almost unable to recognize the morphological changes of ECG signals without tool support. Therefore, an effective computer-aided diagnosis system is needed to solve this problem.
Most ECG classification methods are mainly based on one-dimensional ECG data. These methods usually need to extract the waveform’s characteristics, the interval of adjacent wave, and the amplitude and period of each wave as input. The main difference between them is the selection of the classifier.
Early on, Yuzhen et al. [
2] used the BP neural network to classify the ECG beat, with the classification accuracy rate reaching 93.9%. Martis et al. [
3,
4] proposed discrete cosine transform (DCT) coefficients from the segmented beats of ECGs, which were then subjected to principal component analysis for dimensionality reduction, and a probabilistic neural network (PNN) for automatic classification. They classified the ECG beats into five categories with the highest average sensitivity of 98.69%, specificity of 99.91%, and classification accuracy of 99.52%. Luo et al. used an artificial neural network, based on multi-order feedforward, to classify the ECG beat into six categories, and finally obtained a classification accuracy rate of 90.6% [
5]. Osowski et al. designed a classifier that cascades the fuzzy self-organizing layer and the multi-layer perceptron, and realized seven classifications for ECG beats with a classification accuracy rate of 96% [
6]. Ceylan et al. used feedforward neural networks as the classifier, and they realized the detection of four different arrhythmias with an average accuracy of 96.95% [
7]. Hu extracted features based on multiple discriminant and principal component analysis, and used a support vector machine (SVM) for classification [
8]. Song et al. used a combination of linear discriminant analysis with SVM for six types of arrhythmia [
9]. Melgani and Bazi proposed SVM with particle swarm optimization for the classifier. Finally, they achieved 89.72% overall accuracy with six different arrhythmias [
10]. Martis et al. [
11] used a four-layered feedforward neural network and a least squares support vector machine (LS-SVM) to classify the ECG beats into five categories with highest average accuracy of 93.48%, average sensitivity of 99.27%, and specificity of 98.31%. Pławiak [
12] designed two genetic ensembles of classifiers optimized by classes and by sets, based on an SVM classifier, a 10-fold cross-validation method, layered learning, genetic selection of features, genetic optimization of classifiers parameters, and novel genetic training. The best genetic ensemble of classifiers optimized by sets obtained a classification sensitivity of 17 heart disorders (classes) at a level of 91.40%.
Deep learning was successfully applied to many areas such as recognizing numbers and characters, face recognition, object recognition, and image classification. Deep learning methods are also used effectively in the analysis of bioinformatics signals [
13,
14,
15,
16]. Ubeyli proposed a recurrent neural network (RNN) classifier with an eigenvector-based feature extraction method [
17]. As a result, the model achieved 98.06% average accuracy with four different arrhythmias. Kumar and Kumaraswamy introduced a random forest tree (RFT) as the classifier which used only an RR interval as the classification feature [
18]. Park et al. proposed a K-nearest neighbor (K-NN) classifier for detecting 17 types of ECG beats, which resulted in an average of 97.1% sensitivity and 98.9% specificity [
19]. Jun et al. also introduced K-NN, proposing a parallel K-NN classifier for high-speed arrhythmia detection [
20]. Related to this paper, Kiranyaz et al. introduced a one-dimensional (1D) convolutional neural network (CNN) for the ECG classification, where they used CNN to extract features for one-dimensional ECG signals [
21]; however, the classification accuracy was not higher than our method. Rajpurkar et al. also proposed a one-dimensional CNN classifier that used deeper and more data than the CNN model of Kiranyaz [
22]. Despite using a larger ECG dataset, the classification performance was still lower than our model. The reason is that, although the size of the dataset was increased, the ECG signal used as an input remained in one dimension; thus, the performance improvement was not great even with deep CNN [
23]. Yildirim et al. [
24] designed a new 1D convolutional neural network model and achieved a recognition overall accuracy of 17 cardiac arrhythmia disorders at a level of 91.33%. Acharya et al. [
25] developed a nine-layer deep CNN to automatically identify five different heartbeat types. Their proposed model achieved 94.03% and 93.47% accuracy rates in the original and noise-free ECGs, respectively. Shu et al. [
26] modified the U-net model to perform beat-wise analysis on heterogeneously segmented ECGs of variable lengths derived from the MIT-BIH arrhythmia database, and attained a high classification accuracy of 97.32% in diagnosing cardiac conditions. Chauhan and Vig [
27] used deep long short-term memory (LSTMs) networks to detect abnormal and normal signals in ECG data. The ECG signals used included four different types of abnormal beats. The proposed deep LSTM-based detection system provided 96.45% accuracy on test data. Yildirim [
28] proposed a new model for deep bidirectional LSTM network-based wavelet sequences, and classified the heartbeats obtained from the MIT-BIH arrhythmia database into five different types with a high recognition performance of 99.39%. Tan et al. [
29] implemented LSTM with CNN to automatically diagnose coronary artery disease (CAD) using ECG signals accurately. Warrick and Homosi [
30] proposed a new approach to automatically detect and classify cardiac arrhythmias in ECG records. They used a combination of CNN and LSTM. Shu et al. [
31] also proposed an automated system using a combination of CNN and LSTM for diagnosis of normal sinus rhythm, left bundle branch block, right bundle branch block, atrial premature beats, and premature ventricular contraction on ECG signals. They achieved an accuracy of 98.10%, sensitivity of 97.50%, and specificity of 98.70%. Hwang et al. [
32] proposed an optimal deep learning framework to analyze ECG signals for monitoring mental stress in humans.
In this paper, we propose an ECG classification method using faster regions with a convolutional neural network (Faster R-CNN) with ECG images. This method uses CNN to extract features of ECG images. The reason why we applied two-dimensional CNN by converting the ECG signal into an ECG image in this paper is that two-dimensional convolutional and pooling layers are more suitable for filtering the spatial locality of the ECG images. As a result, higher ECG classification accuracy can be obtained. In addition, the physician can judge the arrhythmia in ECG signals of the patient through vision treatment of the eyes. Therefore, we concluded that applying the two-dimensional CNN model to the ECG image is most similar to the physician’s arrhythmia diagnosis process. Moreover, this method can be applied to ECG signals from various ECG devices with different sampling rates. Before the one-dimensional ECG signals are converted to two-dimensional ECG images, we preprocessed the one-dimensional ECG signals by empirical mode decomposition (EMD) [
33]. Finally, we classified the ECG into five categories with 99.21% average accuracy. Meanwhile, we did a comparative experiment using the OVR SVM algorithm, and the classification result of our method is higher than that of the one versus rest (OVR) SVM [
34] algorithm. At the end of the article, we compared our model with previous works using machine learning algorithms to classify ECG, where the proposed method achieved the best results in average accuracy.
The rest of the paper is structured as follows:
Section 2 introduces the method of ECG signal preprocessing and Faster R-CNN architecture.
Section 3 presents the experimental design based on the Faster R-CNN algorithm.
Section 4 describes the experimental results and the comparative analysis. Conclusions are drawn in
Section 5.