Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration
Abstract
:1. Introduction
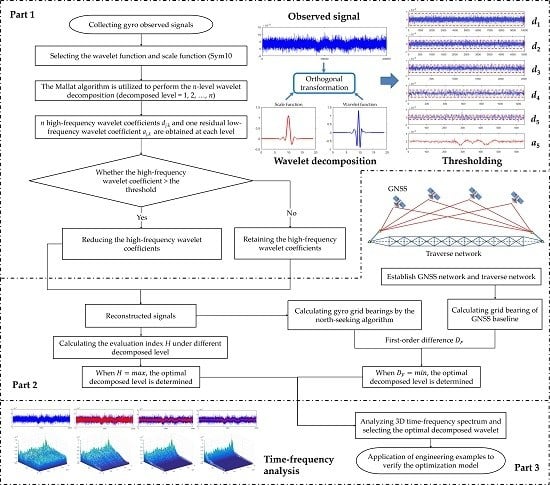
2. Materials and Methods
2.1. Data Characteristics of the GAT
2.2. Basic Theory of Wavelet Transform
2.2.1. Determination of Threshold Function
2.2.2. Reconstruction of Wavelet Coefficient and Time-Frequency Analysis
2.2.3. Determination of the Optimal Decomposed Level
2.3. Experimental Design
2.3.1. Experimental Network
2.3.2. Optimization of the Decomposed Level
2.3.3. Feasibility verification
3. Results and discussion
3.1. Optimization of the Decomposed Level
- Steady signals were collected under ideal observation conditions. Since the observed signals were less affected by the external environment, DF was already relatively small before filtering (Figure 6). The distribution of wavelet coefficients on each frequency band is uniform, and the observed signal contains a significant amount of high frequency random noise (Figure 8a). By increasing the decomposed level from 0 to 6, most of the high-frequency wavelet coefficients had been removed gradually (Figure 8b,c), the reconstructed signal became smoother, and white noise was eliminated (Figure 7a), while the decomposed level had little effect on DF (from 1.5″ to 0.8″) (Figure 6). Consequently, the optimal decomposed level mainly depends on H. When the decomposed level = 6, H = max, and good results both on de-noising (Figure 7a) and corrective effect (Figure 6) were achieved.
- Periodic signals were collected under the conditions where interference can be ignored. Like the pattern of steady signals, high-frequency noise accounts for most of the spectra, while the periodic low-frequency coefficient occupies most of the amplitude energy (Figure 8d). When the decomposed level = 8, most of the Gaussian noise was eliminated, but the time series of signals still retained periodic characteristics (yellow line in Figure 7b) since the low-frequency wavelet coefficients had a large residual in the spectra (Figure 8e). To remove the periodicity and make the signal smoother (red line in Figure 7b), the decomposed level needed to reach 12 (Figure 5 and Figure 6). Consequently, only very small wavelet coefficients (smaller than 2 × 10−7) were left in the spectrum (wavelet in Figure 8f) and DF changed from 2.6″ to 1.3″ (Figure 6). This periodic trend is the weak response to the environmental factors of the torque rectification algorithm of GAT, which belongs to regular systematic error [7]. It affects the signal dispersion (RMSE) but has less influence on the north-seeking result (mean value). Therefore, it is not necessary to completely eliminate the periodic trend in the signal.
- Jitter signals were collected under wind-vibration conditions. Although the high-frequency wavelet coefficients occupied a wide frequency band range, low-frequency wavelet coefficients occupied a larger proportion of energy (Figure 8g), which led to the observed signal containing the jitter trends (Figure 7c). Most high-frequency random noise was removed at the decomposed level = 6. However, residual low-frequency wavelet coefficients remained (Figure 8h), indicating the noise affected by the jitter trend had not been eliminated (yellow line in Figure 7c) and that further decomposing and thresholding needed to be carried out. The comparison of the spectrum at level = 6 (Figure 8h) and level = 9 (Figure 8i) shows that residual wavelet coefficients decreased from 1 × 10-−3 to 2 × 10−7, H changed from 0.8 to 2.3 (Figure 5), DF changed from 2.4″ to 1.1″ (Figure 6), the reconstructed signal became smooth, and the abnormal signals affected by environmental factors were repaired (red line in Figure 7c). Continuing to increase the decomposed level, H gradually converged to a certain value and did not obviously change anymore (Figure 5). However, a negative effect on DF occurred when the decomposed level exceeded 10 (Figure 6), which indicates that an excessive decomposed level increases the risk of reconstructed signal distortion.
- Jumping signals were collected under the condition of ground vibration caused by a vehicle passing. Most of the energy was concentrated in the low-frequency band, and the jumping trend formed a peak in the low-frequency band in the spectrum (Figure 8j). The energy of high-frequency noise seemed negligible compared with the peak, and almost all high-frequency noise was eliminated at the decomposed level = 7, while the energy of the peak remained in the spectrum (Figure 8k). The time series shows that the jumping trend had not been removed entirely (Figure 7d), and the slopes of H and DF were also not large (Figure 5 and Figure 6); DF changed from 7.4″ to 6.9″. With an increase in the decomposed level from 7 to 10, the slope of H and DF increased significantly (Figure 5 and Figure 6). The peak flattened (Figure 8l) and the jumping trend was corrected with a corrective effect of 1.3″ achieved (from 6.9″ to 5.6″) (Figure 6 and Figure 7d). After increasing the decomposed level from 10 to 12 (H = max, DF = min), a change of H was no longer obvious (Figure 5), while DF decreased dramatically (from 5.6″ to 0.5″) (Figure 6). Although this seems to be beneficial to the north-seeking results, it is not; drastic change is risky. Even though the result shows that the gyro grid bearing after filtering is closer to the true north, similar to the case of the jitter signals, an excessive decomposed level causes instability of DF, which reduces the reliability of north-seeking results.
3.2. Feasibility Verification
4. Conclusions
- The observed signal of a north-seeking gyro sensor is affected by different environmental factors and shows different non-stationary characteristics, so that the selection of the wavelet decomposed level for de-noising is adapted to different types of observed signals.
- Using the constraints of high-precision external verification conditions (GNSS grid bearings) combined with the prior observed signals will provide empirical values for the wavelet decomposed level and optimize the efficiency of the filtering model. This method of determining the optimal wavelet decomposed level is able to be used not only in GAT, but also in other types of gyroscope sensors.
- In the application of tunnel surveying engineering, which is vulnerable to complex environmental factors, the optimized model eliminates the influence of external disturbances on the observed signal to a certain extent and enhances the north-seeking accuracy of gyro sensors.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bai, J.M.; Zhao, G.S.; Rong, H.J.; Wang, X.H. Seeker-Azimuth Determination with Gyro Rotor and Optoelectronic Sensors. Sensors 2018, 18, 1256. [Google Scholar] [CrossRef] [PubMed]
- Lauf, G.B. The Gyrotheodolite and Its Application in The Industry of South Africa. J. S. Afr. Inst. Min. Metall. 1963, 349–386. [Google Scholar]
- Velasco-Gómez, J.; Prieto, J.F.; Molina, I.; Herrero -Tejedor, T.R.; Fábrega, J.; Pérez-Martín, E. Use of the Gyrotheodolite in Underground Networks of Long High-speed Railway Tunnels. Surv. Rev. 2016, 48, 329–337. [Google Scholar] [CrossRef]
- Li, K.; Wang, L.; Lv, Y.H.; Gao, P.Y.; Song, T.X. Research on the Rapid and Accurate Positioning and Orientation Approach for Land Missile-Launching Vehicle. Sensors 2015, 15, 26606–26620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, Z.; Yang, Z.Q.; Zhang, Z. Study on Automatic North-Seeking Key Technologies of Maglev Gyroscope. Open Mech. Eng. J. 2013, 7, 83–89. [Google Scholar] [Green Version]
- Jia, Z.Y.; Ma, X.; Liu, W.; Lu, W.B.; Li, X.; Chen, L.; Wang, Z.Q.; Cui, X.C. Pose Measurement Method and Experiments for High-speed Rolling Targets in a Wind Tunnel. Sensors 2014, 14, 23933–23953. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.X.; Li, B.J.; Zhang, Y.Y.; Yan, J.; Zhang, C. Numerical Investigation of Heat-Insulating Layers in A Cold Region Tunnel:Taking into Account Airflow and Heat Transfer. Appl. Sci. 2017, 7, 679. [Google Scholar] [CrossRef]
- Narayananellore, S.K.; Doko, N.; Matsuo, N.; Saito, H.; Yuasa, S. Effect of MgO Underlying Layer on the Growth of GaOx Tunnel Barrier in Epitaxial Fe/GaOx/(MgO)/Fe Magnetic Tunnel Junction Structure. Sensors 2017, 17, 2424. [Google Scholar] [CrossRef]
- Yi, X.F.; Zhang, J.; Fan, T.H.; Tian, B.F.; Jiang, C.D. Design of Meter-Scale Antenna and Signal Detection System for Underground Magnetic Resonance Sounding in Mines. Sensors 2018, 18, 848. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Z.Q.; Shi, Z.; Liu, C.C.; Yin, H.Q.; Zhang, X.Z. Adjustment Options for A Survey Network with Magnetic Levitation Gyro Data in An Immersed Under-Sea Tunnel. Surv. Rev. 2019, 6265. [Google Scholar] [CrossRef]
- Combes, J.M.; Grossmann, A.; Tchamitchian, P. Wavelet: Time-Frequency Methods and Phase Space. Inverse Probl. Theor. Imaging 1989, 1, 2477–2478. [Google Scholar]
- Dabuechies, I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis. IEEE Trans. Inf. Theor. 2002, 36, 961–1005. [Google Scholar] [CrossRef]
- Daubechies, I.; Sweldens, W. Factoring Wavelet Transforms into Lifting Steps. J. Fourier Anal. Appl. 1998, 4, 247–269. [Google Scholar] [CrossRef]
- Sweldens, W. Lifting Scheme: A New Philosophy in Biorthogonal Wavelet Constructions. In Proceedings of the Wavelet Applications in Signal and Image Processing III, San Diego, CA, USA, 1 September 1995; pp. 68–79. [Google Scholar]
- Boles, W.W.; Boashash, B. A Human Identification Technique Using Images of the Iris and Wavelet Transform. IEEE Trans. Signal Process. 2002, 46, 1185–1188. [Google Scholar] [CrossRef]
- Gradolewski, D.; Magenes, G.; Johansson, S.; Kulesza, W. A Wavelet Transform-Based Neural Network Denoising Algorithm for Mobile Phonocardiography. Sensors 2019, 19, 957. [Google Scholar] [CrossRef] [PubMed]
- Kutlu, H.; Avcı, E. A Novel Method for Classifying Liver and Brain Tumors Using Convolutional Neural Networks, Discrete Wavelet Transform and Long Short-Term Memory Networks. Sensors 2019, 19, 1992. [Google Scholar] [CrossRef] [PubMed]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of The Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- To, A.C.; Moore, J.R.; Glaser, S.D. Wavelet Denoising Techniques with Applications to Experimental Geophysical Data. Signal Process. 2009, 89, 144–160. [Google Scholar] [CrossRef]
- Chang, S.G.; Yu, B.; Vetterli, M. Adaptive Wavelet Thresholding for Image Denoising and Compression. IEEE Trans. Image Process. 2000, 9, 1532–1546. [Google Scholar] [CrossRef]
- Antonini, M.; Barlaud, M.; Mathieu, P.; Daubechies, I. Image Coding Using Wavelet Transform. IEEE Trans. Image Process. 1992, 1, 205–220. [Google Scholar] [CrossRef]
- Yang, Y.; Tong, S.; Huang, S.Y.; Lin, P. Dual-Tree Complex Wavelet Transform and Image Block Residual-Based Multi-Focus Image Fusion in Visual Sensor Networks. Sensors 2014, 14, 22408–22430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, Z.; Balch, T.; Dellaert, F. An MCMC-Based Particle Filter for Tracking Multiple Interacting Targets. Comput. Vis.-ECCV 2004, 279–290. [Google Scholar] [CrossRef]
- Chang, C.; Ansari, R. Kernel Particle Filter for Visual Tracking. IEEE Signal Process. Lett. 2005, 12, 242–245. [Google Scholar] [CrossRef]
- Breitenstein, M.D.; Reichlin, F.; Leibe, B.; Koller-Meier, E.; Gool, L.V. Robust Tracking-by-Detection Using A Detector Confidence Particle Filter. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 1515–1522. [Google Scholar]
- Molina-Tenorio, Y.; Prieto-Guerrero, A.; Aguilar-Gonzalez, R. A Novel Multiband Spectrum Sensing Method Based on Wavelets and The Higuchi Fractal Dimension. Sensors 2019, 19, 1322. [Google Scholar] [CrossRef] [PubMed]
- Selim, H.; Prieto, M.D.; Trull, J.; Romeral, L.; Cojocaru, C. Laser Ultrasound inspection Based on Wavelet Transform and Data Clustering for Defect Estimation in Metallic Samples. Sensors 2019, 19, 573. [Google Scholar] [CrossRef] [PubMed]
- Sabat, S.L.; Giribabu, N.; Nayak, J.; Krishnaprasad, K. Characterization of Fiber Optics Gyro and Noise Compensation Using Discrete Wavelet Transform. In Proceedings of the 2009 Second International Conference on Emerging Trends in Engineering & Technology, Nagpur, India, 16–18 December 2009; pp. 909–913. [Google Scholar]
- Li, J.L.; Xu, H.L.; He, Q. Research and Improvement of Denoising Method of Fiber Optic Gyroscope Based on Wavelet Packet Analysis. Acta Opt. Sin. 2010, 30, 2224–2228. [Google Scholar]
- Mao, B.; Wei, W.J.; Tong, W.J.; Mei, Z.X. MEMS Gyro Denoising Based on Second Generation Wavelet Transform. In Proceedings of the 2010 1st International Conference on Pervasive Computing, Harbin, China, 17–19 September 2010; pp. 255–258. [Google Scholar]
- Liu, F.Q.; Liu, F.M.; Wang, W.J.; Xu, B. MEMS Gyro’s Output Signal De-Noising Based on Wavelet Analysis. In Proceedings of the 2007 International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007; pp. 1288–1293. [Google Scholar]
- Lee, W.; Park, C.G. Double Fault Detection of Cone-Shaped Redundant IMUs Using Wavelet Transformation and EPSA. Sensors 2014, 14, 3428–3444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yi, T.H.; Li, H.N.; Zhao, X.Y. Noise Smoothing for Structural Vibration Test Signals Using an Improved Wavelet Thresholding Technique. Sensors 2012, 12, 11205–11220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ayrulu-Erdem, B.; Barshan, B. Leg Motion Classification with Artificial Neural Networks Using Wavelet-Based Features of Gyroscope Signals. Sensors 2011, 11, 1721–1743. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, W.D.; Xiang, C.L.; Han, L.J.; Nie, H.Z. A De-Noising Method Using The Improved Wavelet Threshold Function Based on Noise Variance Estimation. Mech. Syst. Signal Process. 2018, 99, 30–46. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Gong, Y.; Shi, Z.; Yun, L. Change Monitoring of Earth Rotation Parameter with Maglev Gyroscope Precessional Torque. Trans. Nonferrous Met. Soc. China 2011, 21, s589–s593. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Shi, Z.; Yang, J.H. North Seeking Principle and Measurement Application of Magnetically Suspended Gyroscope; Surveying and Mapping Press: Beijing, China, 2017. [Google Scholar]
- Cheng, G.D. A Roadbed Cooling Approach for The Construction of Qinghai–Tibet Railway. Cold Reg. Sci. Technol. 2005, 42, 169–176. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Z.Q.; Ji, G.F. The Determination of Plumb-Line Deviation by Adopting GNSS/Leveling Method in Super Long Tunnel Break-Through Measurement. In China Satellite Navigation Conference (CSNC) 2017 Proceedings: Volume I; Sun, J., Liu, J., Yang, Y., Fan, S., Yu, W., Eds.; Springer: Singapore, 2017; pp. 107–125. [Google Scholar]
- Miao, L.J. Application of wavelet analysis in the signal processing of the fiber optic gyro. J. Astronaut 2000, 21, 42–46. [Google Scholar]
- Ren, C.H.; Xiong, L.X.; Zhao, X.J.; Pan, Y.J. The Application of Wavelet Threshold—Value Filter in Signal Processing of Fiber Optic Gyroscope. Piezoelectrics Acoustooptics 2010, 32, 957–959. [Google Scholar]
- Li, Q.; Teng, J.F.; Wang, X.; Zhang, Y.Q.; Guo, J.C. Research of Gyro Signal De-Noising with Stationary Wavelets Transform. In Proceedings of the IEEE Ccece Canadian Conference on Electrical & Computer Engineering, Montreal, QC, Canada, 4–7 May 2003; pp. 1989–1992. [Google Scholar]
- Ma, J.; Shi, Z.; Yang, Z.Q. Variable precision adjustment optimization of a long traverse with Maglev gyro observations. In Proceedings of the 16th International Congress for Mine Surveying, Brisbane, Australia, 12–16 September 2016; pp. 81–85. [Google Scholar]
- Mallat, S.G. Multiresolution Approximations and Wavelet Orthonormal Bases of L 2 (R). Trans. Am. Math. Soc. 1989, 315, 69–87. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way; Academic Press: New York, NY, USA, 2008; pp. 98–99. [Google Scholar]
- Dellwo, V. Rhythm and Speech Rate: A Variation Coefficient for C. In Language and Language-Processing; Karnowski, P., Szigeti, I., Eds.; Peter Lang: Frankfurt am Main, Germany, 2006; pp. 231–241. [Google Scholar]
- Huang, S.X.; Li, G.Q.; Wang, X.P.; Zhang, W. Geodetic Network Design and Data Processing for Hong Kong–Zhuhai–Macau Link Immersed Tunnel. Surv. Rev. 2017, 114–122. [Google Scholar] [CrossRef]
- Trimble. User Guide for Trimble R7 GPS Receiver. Available online: http://www.terraseis.com/ckfinder/userfiles/files/Trimble%20R7GNSS.pdf (accessed on 15 August 2019).
- Herring, T.A.; Floyd, M.A.; King, R.W.; McClusky, S.C. GLOBK Reference Manul Global Kalman filter VLBI and GPS analysis program Release 10.6. Available online: http://geoweb.mit.edu/gg/GLOBK_Ref.pdf (accessed on 15 August 2019).
- Leica Geosystems. Leica TPS1200+TS30/TM30 Technical Reference Manual. Available online: http://www.grad-gon.info/download/manuals/TPS_1200+/en/TPS1200+_TS30_TM30_TechRef_en.pdf (accessed on 15 August 2019).
- Johnston, A. Lateral Refraction in Tunnels. Surv. Rev. 1991, 31, 201–220. [Google Scholar] [CrossRef]










| Type of Network | Number of Observations | Instrument | Precision Indexes | Standard Deviation of the Weakest Points |
|---|---|---|---|---|
| Global Navigation Satellite System (GNSS) network | 10 points simultaneously observed by GPS for 76 hours | Trimble R7 GPS receiver [48] | Static plane accuracy ± (3 mm + 0.1 ppm) | 1.2 mm (Use GLOBK Software for 3D network adjustment [49]) |
| Traverse network | Horizontal directions: 221 (9 repeat observations per stations) Horizontal distances: 119 (9 repeat observations per stations) | Leica TS30 total station [50] | Direction precision ± 0.5″ Distance precision ± (0.6 mm + 1 ppm) | 1.0 mm (Use COSA-CODAPS Software for network adjustment) |
| Type of Survey Lines | Parameters of Survey Lines | Experimental Parameters of Gyro Observation | |||
|---|---|---|---|---|---|
| Length | Relative Accuracy of Grid Bearing | Repeat Observation Per Station | Observation Environment | Standard Deviation of Gyro Bearing | |
| Gyro calibration line (GNSS baseline) | 613 m | 0.4″ | 4 | Stable | 1.3″ |
| GNSS reference baseline for filtering experiment | 524 m | 0.5″ | 4 | Stable, vehicle passing or wind vibration | 6.2″ |
| Gyro line 1 | 744 m | 1.1″ | 3 | Wind vibration and vehicle passing | 2.3″ |
| Gyro line 2 | 696 m | 1.3″ | 3 | Vehicle passing | 1.5″ |
| Gyro line 3 | 319 m | 1.8″ | 3 | Stable | 1.3″ |
| Gyro line 4 | 692 m | 1.3″ | 3 | Weak wind vibration | 1.8″ |
| Gyro line 5 | 244 m | 1.9″ | 3 | Stable | 2.0″ |
| Criteria | Steady | Periodic | Jitter | Jumping |
|---|---|---|---|---|
| H = max | 6 | 12 | 10 | 12 |
| DF = min | 6 | 11 | 9 | 12 |
| Comprehensive evaluation | 6 | 8 | 9 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Yang, Z.; Shi, Z.; Zhang, X.; Liu, C. Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration. Sensors 2019, 19, 3624. https://doi.org/10.3390/s19163624
Ma J, Yang Z, Shi Z, Zhang X, Liu C. Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration. Sensors. 2019; 19(16):3624. https://doi.org/10.3390/s19163624
Chicago/Turabian StyleMa, Ji, Zhiqiang Yang, Zhen Shi, Xuewei Zhang, and Chenchen Liu. 2019. "Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration" Sensors 19, no. 16: 3624. https://doi.org/10.3390/s19163624
APA StyleMa, J., Yang, Z., Shi, Z., Zhang, X., & Liu, C. (2019). Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration. Sensors, 19(16), 3624. https://doi.org/10.3390/s19163624