Screen-Printed, Pure Carbon-Black Thermocouple Fabrication and Seebeck Coefficients
Abstract
:1. Introduction
2. Materials and Methods
- Electrodag PR-406B by Henkel (hereafter referred to as “406”)
- EDAG 109 E&C by Loctite (hereafter referred to as “109”)
- SD 2842 HAL by Peters (hereafter referred to as “2842”)
- SD 2843 HAL by Peters (hereafter referred to as “2843”)
3. Results
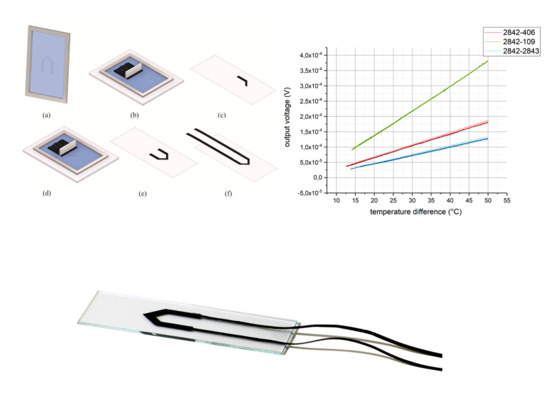
3.1. Measurement Setup
3.2. Characterization of the Pure Carbon-Black Thermocouples and Determination of the Seebeck Coefficients
3.3. Verification of the Seebeck Coefficients
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Childs, P.R.N.; Greenwood, J.R.; Long, C.A. Review of temperature measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. [Google Scholar] [CrossRef] [Green Version]
- Nicholas, J.V.; White, D.R. Traceable Temperatures: An introduction to temperature measurement and calibration, 2nd edn. Meas. Sci. Technol. 2002, 13, 1651. [Google Scholar] [CrossRef]
- Stephenson, R.J. Bimaterials Thermometers—The Measurement Instrumentation and Sensors Handbook; CRC Press: Boca Raton, FI, USA, 1999. [Google Scholar]
- Wise, J.A. Liquid-in-Glass Thermometry; Final Report National Bureau of Standards: Boulder, CO, USA, 1976.
- Strouse, G.F.; Mangum, B.W.; Pokhodun, A.I.; Moiseeva, N.P. Investigation of high-temperature platinum resistance thermometers at temperatures up to 962 °C, and in some cases 1064 °C. Temp. Meas. Control Sci. Ind. 1992, 6, 389–394. [Google Scholar]
- Szmyrka-Grzebyk, A.; Lipiński, L. Linear diode thermometer in the 4–300 K temperature range. Cryogenics 1995, 35, 281–284. [Google Scholar] [CrossRef]
- Park, J.S.; Choi, C.K.; Kihm, K.D. Temperature measurement for a nanoparticle suspension by detecting the Brownian motion using optical serial sectioning microscopy (OSSM). Meas. Sci. Technol. 2005, 16, 1418–1429. [Google Scholar] [CrossRef]
- Millen, J.; Deesuwan, T.; Barker, P.; Anders, J. Nanoscale temperature measurements using non-equilibrium Brownian dynamics of a levitated nanosphere. Nat. Nanotechnol. 2014, 9, 425–429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lawless, W.N.; Clark, C.F.; Arenz, R.W. Method for measuring specific heats in intense magnetic fields at low temperatures using capacitance thermometry. Rev. Sci. Instrum. 1982, 53, 1647–1652. [Google Scholar] [CrossRef]
- Wraith, J.M.; Or, D. Temperature effects on soil bulk dielectric permittivity measured by time domain reflectometry: Experimental evidence and hypothesis development. Water Resour. Res. 1999, 35, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.J. Optical measurement of temperature. Meas. Technol. Heat Transf. 1970, 177–228. Available online: https://experts.umn.edu/en/publications/optical-measurement-of-temperature (accessed on 28 November 2018).
- MacDonald, D.K.C. Thermoelectricity: An Introduction to the Principles; John Wiley & Sons, Inc.: New York, NY, USA, 1962. [Google Scholar]
- Kasap, S. Thermoelectric Effects in Metals: Thermocouples; Department of Electrical Engineering, University of Saskatchewan: Saskatoon, SK, Canada, 2001. [Google Scholar]
- Herring, C. Theory of the Thermoelectric Power of Semiconductors. Phys. Rev. 1954, 96, 1163–1187. [Google Scholar] [CrossRef]
- Goldsmid, H.J.; Sharp, J.W. Estimation of the thermal band gap of a semiconductor from seebeck measurements. J. Electron. Mater. 1999, 28, 869–872. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, X.; Li, K.; Li, D.; Luo, Y.; Li, H.; Song, W.; Chen, L.; Meng, Q. Application of carbon materials as counter electrodes of dye-sensitized solar cells. Electrochem. Commun. 2007, 9, 596–598. [Google Scholar] [CrossRef]
- Wang, L.; Tay, B.; See, K.; Sun, Z.; Tan, L.; Lua, D. Electromagnetic interference shielding effectiveness of carbon-based materials prepared by screen printing. Carbon N. Y. 2009, 47, 1905–1910. [Google Scholar] [CrossRef]
- Ku, Z.; Rong, Y.; Xu, M.; Liu, T.; Han, H. Full Printable Processed Mesoscopic CH3NH3PbI3/TiO2 Heterojunction Solar Cells with Carbon Counter Electrode. Nat. Sci. Rep. 2013, 3, 3132. [Google Scholar] [CrossRef] [PubMed]
- Nonoguchi, Y.; Ohashi, K.; Kanazawa, R.; Ashiba, K.; Hata, K.; Nakagawa, T.; Adachi, C.; Tanase, T.; Kawai, T. Systematic Conversion of Single Walled Carbon Nanotubes into n-type Thermoelectric Materials by Molecular Dopants. Sci. Rep. 2013, 3, 3344. [Google Scholar] [CrossRef] [PubMed]
- Liebscher, M.; Gärtner, T.; Tzounis, L.; Mičušík, M.; Pötschke, P.; Stamm, M.; Heinrich, G.; Voit, B. Influence of the MWCNT surface functionalization on the thermoelectric properties of melt-mixed polycarbonate composites. Compos. Sci. Technol. 2014, 101, 133–138. [Google Scholar] [CrossRef]
- Lee, B.-L. Electrical conductivity of carbon black filled polymers—Effects of morphology and processing. J. Vinyl Addit. Technol. 1993, 15, 173–176. [Google Scholar] [CrossRef]
- Poehler, T.O.; Katz, H.E. Innovative Thermoelectric Materials. In Innovative Thermoelectric Materials; Imperial College Press: London, UK, 2016; pp. 1–37. [Google Scholar]
- Bubnova, O.; Khan, Z.U.; Malti, A.; Braun, S.; Fahlman, M.; Berggren, M.; Crispin, X. Optimization of the thermoelectric figure of merit in the conducting polymer poly (3, 4-ethylenedioxythiophene). Nat. Mater. 2011, 10, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Cusack, N.; Kendall, P. The Absolute Scale of Thermoelectric Power at High Temperature. Proc. Phys. Soc. 1958, 72, 898–901. [Google Scholar] [CrossRef]
- Van Herwaarden, A.W.; Sarro, P.M. Thermal Sensors Based on the Seebeck Effect. Sens. Actuators 1986, 10, 321–346. [Google Scholar] [CrossRef]






| Ink | Solids Content by Weight (%) | Viscosity (Pa∙s) | Density (g/cm3) | Sheet Resistivity (Ω/sq/25 µm) |
|---|---|---|---|---|
| 406 | 56–60 | 35–45 | 1.25 | <10 |
| 109 | 40 | 2.2 | 1.03 | <30 |
| 2842 | 76–84 | 29 | 1.37 | 14 |
| 2843 | 73–77 | 17 | 1.27 | 13 |
| Material | Seebeck Coefficient (µV/K) |
|---|---|
| Gold | −1.94 [23] |
| 2842 | |
| 406 | |
| 109 | |
| 2843 | |
| Platinum | −5.28 [24] |
| Palladium | −9.00 [24] |
| Copper | 1.83 [24] |
| Thermocouple | Output (Predicted) (µV/K) | Output (Measured) (µV/K) | Deviation from the Predicted Value (%) |
|---|---|---|---|
| 406-109 | 4.07 | 4.29 | 5.4 |
| 2843-109 | 5.19 | 5.24 | 0.96 |
| 2843-406 | 1.12 | 1.13 | 0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Offenzeller, C.; Knoll, M.; Jakoby, B.; Hilber, W. Screen-Printed, Pure Carbon-Black Thermocouple Fabrication and Seebeck Coefficients. Sensors 2019, 19, 403. https://doi.org/10.3390/s19020403
Offenzeller C, Knoll M, Jakoby B, Hilber W. Screen-Printed, Pure Carbon-Black Thermocouple Fabrication and Seebeck Coefficients. Sensors. 2019; 19(2):403. https://doi.org/10.3390/s19020403
Chicago/Turabian StyleOffenzeller, Christina, Marcel Knoll, Bernhard Jakoby, and Wolfgang Hilber. 2019. "Screen-Printed, Pure Carbon-Black Thermocouple Fabrication and Seebeck Coefficients" Sensors 19, no. 2: 403. https://doi.org/10.3390/s19020403
APA StyleOffenzeller, C., Knoll, M., Jakoby, B., & Hilber, W. (2019). Screen-Printed, Pure Carbon-Black Thermocouple Fabrication and Seebeck Coefficients. Sensors, 19(2), 403. https://doi.org/10.3390/s19020403