Enhancing Compression Level for More Efficient Compressed Sensing and Other Lessons from NMR Spectroscopy
Abstract
:1. Introduction
2. Theory
- highly probable exact recovery of a sparse signal based on limited information about it;
- highly probable approximately exact recovery of a compressible signal based on limited information about it.
3. Results and Discussion
3.1. Lesson 1: Reduce the Number of Peaks
3.2. Lesson 2: Minimize Dynamic Range
3.3. Lesson 3: Pre-Processing
3.4. Lesson 4: Match Sampling with the Decay
3.5. Lesson 5: Non-Stationarity
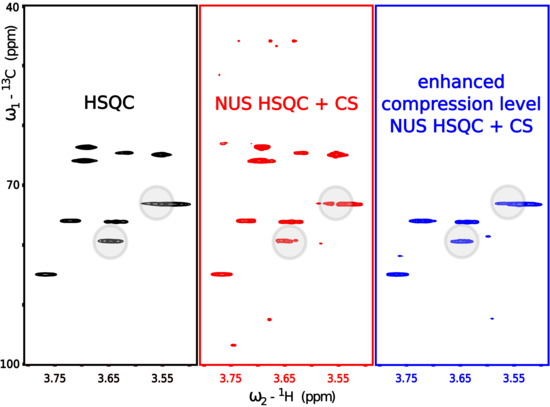
3.6. Practical Example
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CPMG | Carr–Purcell–Meiboom–Gill |
| CS | Compressed Sensing |
| DOAJ | Directory of open access journals |
| FID | Free Induction Decay |
| FT | Fourier Transform |
| HSQC | Heteronuclear Single-Quantum Correlation |
| IPAP | In-phase anti-phase |
| IRLS | Iteratively Re-weighted Least Squares |
| IST | Iterative Soft Thresholding |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MW | Molecular weight |
| NMR | Nuclear Magnetic Resonance |
| NOESY | Nuclear Overhauser Effect Spectroscopy |
| OMP | Orthogonal matching pursuit |
| PS | Pure-shift (NMR) |
| PSF | Point spread function |
| RF | Radio frequency |
| RIP | Restricted isometry property |
| ROESY | Rotating Frame Overhauser Effect Spectroscopy |
| SNR | Signal-to-noise ratio |
| TOCSY | Total Correlation Spectroscopy |
| UUP | Uniform Uncertainty Principle |
| VD | Virtual Decoupling |
| VE | Virtual Echo |
References
- Simpson, J.H. Organic Structure Determination Using 2-D NMR Spectroscopy; Academic Press: San Diego, CA, USA, 2012. [Google Scholar] [CrossRef]
- Forseth, R.; Schroeder, F. NMR-spectroscopic analysis of mixtures: From structures to function. Curr. Opin. Chem. Biol. 2012, 15, 38–47. [Google Scholar] [CrossRef] [Green Version]
- Dass, R.; Koźmiński, W.; Kazimierczuk, K. Analysis of complex reacting mixtures by time-resolved 2D NMR. Anal. Chem. 2015, 87, 1337–1343. [Google Scholar] [CrossRef]
- Dinges, S.S.; Hohm, A.; Vandergrift, L.A.; Nowak, J.; Habbel, P.; Kaltashov, I.A.; Cheng, L.L. Cancer metabolomic markers in urine: Evidence, techniques and recommendations. Nat. Rev. Urol. 2019, 16, 339–362. [Google Scholar] [CrossRef]
- Sattler, M.; Heidelberg, E. Introduction to biomolecular NMR spectroscopy. Science 2004, 1–18. [Google Scholar]
- Ernst, R.R.; Anderson, W.A. Application of Fourier Transform Spectroscopy to Magnetic Resonance. Rev. Sci. Instrum. 1966, 37, 93–102. [Google Scholar] [CrossRef]
- Jeener, J. AMPERE International Summer School. Basko Polje Yugoslavia 1971, 197. [Google Scholar]
- Ying, J.; Barnes, C.A.; Louis, J.M.; Bax, A. Importance of time-ordered non-uniform sampling of multi-dimensional NMR spectra of Aβ1–42 peptide under aggregating conditions. J. Biomol. NMR 2019, 73, 429–441. [Google Scholar] [CrossRef] [PubMed]
- Nyquist, H. Certain topics in telegraph transmission theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Szántay, C. NMR and the uncertainty principle: How to and how not to interpret homogeneous line broadening and pulse nonselectivity. IV. Uncertainty. Concept. Magn. Reson. A 2008, 32A, 373–404. [Google Scholar] [CrossRef]
- Mobli, M.; Hoch, J.C. Nonuniform sampling and non-Fourier signal processing methods in multidimensional NMR. Prog. Nucl. Mag. Res. Spectrosc. 2014, 83, 21–41. [Google Scholar] [CrossRef] [Green Version]
- Matsuki, Y.; Konuma, T.; Fujiwara, T.; Sugase, K. Boosting protein dynamics studies using quantitative nonuniform sampling NMR spectroscopy. J. Phys. Chem. B 2011, 115, 13740–13745. [Google Scholar] [CrossRef] [PubMed]
- Qu, X.; Mayzel, M.; Cai, J.F.; Chen, Z.; Orekhov, V. Accelerated NMR spectroscopy with low-rank reconstruction. Angew. Chem. Int. Ed. Engl. 2015, 54, 852–854. [Google Scholar] [CrossRef] [PubMed]
- Kazimierczuk, K.; Orekhov, V. Accelerated NMR spectroscopy by using compressed sensing. Angew. Chem. Int. Ed. Engl. 2011, 50, 5556–5559. [Google Scholar] [CrossRef] [PubMed]
- Holland, D.J.; Bostock, M.J.; Gladden, L.F.; Nietlispach, D. Fast multidimensional NMR spectroscopy using compressed sensing. Angew. Chem. Int. Ed. Engl. 2011, 50, 6548–6551. [Google Scholar] [CrossRef] [PubMed]
- Qu, X.; Guo, D.; Cao, X.; Cai, S.; Chen, Z. Reconstruction of self-sparse 2D NMR spectra from undersampled data in the indirect dimension. Sensors 2011, 11, 8888–8909. [Google Scholar] [CrossRef] [Green Version]
- Rani, M.; Dhok, S.B.; Deshmukh, R.B. A Systematic Review of Compressive Sensing: Concepts, Implementations and Applications. IEEE Access 2018, 6, 4875–4894. [Google Scholar] [CrossRef]
- Holland, D.J.; Gladden, L.F. Less is more: How compressed sensing is transforming metrology in chemistry. Angew. Chem. Int. Ed. Engl. 2014, 53, 13330–13340. [Google Scholar] [CrossRef]
- Hyberts, S.; Milbradt, A.; Wagner, A.; Arthanari, H.; Wagner, G. Application of iterative soft thresholding for fast reconstruction of NMR data non-uniformly sampled with multidimensional Poisson Gap scheduling. J. Biomol. NMR 2012, 52. [Google Scholar] [CrossRef] [Green Version]
- Kazimierczuk, K.; Orekhov, V.Y. A comparison of convex and non-convex compressed sensing applied to multidimensional NMR. J. Magn. Reson. 2012, 223, 1–10. [Google Scholar] [CrossRef]
- Shchukina, A.; Kasprzak, P.; Dass, R.; Nowakowski, M.; Kazimierczuk, K. Pitfalls in compressed sensing reconstruction and how to avoid them. J. Biomol. NMR 2017, 68, 79–98. [Google Scholar] [CrossRef] [Green Version]
- Coggins, B.E.; Venters, R.A.; Zhou, P. Radial sampling for fast NMR: Concepts and practices over three decades. Prog. Nucl. Mag. Res. Spectrosc. 2010, 57, 381–419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brüschweiler, R.; Zhang, F. Covariance nuclear magnetic resonance spectroscopy. J. Chem. Phys. 2004, 120, 5253–5260. [Google Scholar] [CrossRef] [PubMed]
- Koehl, P. Linear prediction spectral analysis of NMR data. Prog. Nucl. Mag. Res. Spectrosc. 1999, 34, 257–299. [Google Scholar] [CrossRef]
- Foroozandeh, M.; Jeannerat, D. Reconstruction of full high-resolution HSQC using signal split in aliased spectra. Magn. Reson. Chem. 2015, 53, 894–900. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inform. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inform. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Foucart, S.; Rauhut, H. A Mathematical Introduction to Compressive Sensing; Wiley: Hoboken, NJ, USA, 2010; p. 526. [Google Scholar]
- Candes, E.J. The restricted isometry property and its implicationsfor compressed sensing. C. R. Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef] [Green Version]
- Rovnyak, D.; Sarcone, M.; Jiang, Z. Sensitivity enhancement for maximally resolved two-dimensional NMR by nonuniform sampling. Magn. Reson. Chem. 2011, 483–491. [Google Scholar] [CrossRef]
- Palmer, M.R.; Suiter, C.L.; Henry, G.E.; Rovnyak, J.; Hoch, J.C.; Polenova, T.; Rovnyak, D. Sensitivity of nonuniform sampling NMR. J. Phys. Chem. B 2015, 119, 6502–6515. [Google Scholar] [CrossRef] [Green Version]
- Zangger, K. Pure shift NMR. Prog. Nucl. Mag. Res. Spectrosc. 2015, 86–87, 1–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castañar, L. Pure shift 1H NMR: What is next? Magn. Reson. Chem. 2017, 55, 47–53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aguilar, J.A.; Kenwright, A.M. Compressed NMR: Combining compressive sampling and pure shift NMR techniques. Magn. Reson. Chem. 2018, 56, 983–992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ndukwe, I.E.; Shchukina, A.; Kazimierczuk, K.; Butts, C.P. Rapid and safe ASAP acquisition with EXACT NMR. Chem. Commun. 2016, 52, 12769–12772. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ndukwe, I.; Shchukina, A.; Kazimierczuk, K.; Cobas, C.; Butts, C. EXtended ACquisition Time (EXACT) NMR—A Case for ’Burst’ Non-Uniform Sampling. ChemPhysChem 2016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ndukwe, I.; Shchukina, A.; Zorin, V.; Cobas, C.; Kazimierczuk, K.; Butts, C. Enabling Fast Pseudo-2D NMR Spectral Acquisition for Broadband Homonuclear Decoupling: The EXACT NMR Approach. ChemPhysChem 2017, 18, 2081–2087. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shchukina, A.; Kaźmierczak, M.; Kasprzak, P.; Davy, M.; Akien, G.R.; Butts, C.P.; Kazimierczuk, K. Accelerated acquisition in pure-shift spectra based on prior knowledge from 1H NMR. Chem. Commun. 2019, 55, 9563–9566. [Google Scholar] [CrossRef]
- Mobli, M.; Miljenović, T.M. Framework for and evaluation of bursts in random sampling of multidimensional NMR experiments. J. Magn. Reson. 2019, 300, 103–113. [Google Scholar] [CrossRef]
- Davis, D.G. Improved multiplet editing of proton-detected, heteronuclear shift-correlation spectra. J. Magn. Reson. (1969) 1991. [Google Scholar] [CrossRef]
- Kay, L.E.; Bax, A. Separation of NH and NH2 resonances in 1H-detected heteronuclear multiple-quantum correlation spectra. J. Magn. Reson. (1969) 1989. [Google Scholar] [CrossRef]
- Jaravine, V.A.; Zhuravleva, A.V.; Permi, P.; Ibraghimov, I.; Orekhov, V. Hyperdimensional NMR Spectroscopy with Nonlinear Sampling. J. Am. Chem. Soc. 2008, 130, 3927–3936. [Google Scholar] [CrossRef] [PubMed]
- Dötsch, V.; Wagner, G. Editing for amino-acid type in CBCACONH experiments based on the 13 Cβ- 13 Cγ coupling. J. Magn. Reson. Ser. B 1996, 111, 310–313. [Google Scholar] [CrossRef] [PubMed]
- Grzesiekt, S.; Bax, A. Correlating Backbone Amide and Side Chain Resonances in Larger Proteins by Multiple Relayed Triple Resonance NMR. J. Am. Chem. Soc. 1992, 114, 6291–6293. [Google Scholar] [CrossRef]
- Piai, A.; Gonnelli, L.; Felli, I.; Pierattelli, R.; Kazimierczuk, K.; Grudziaz, K.; Koźmiński, W.; Zawadzka-Kazimierczuk, A. Amino acid recognition for automatic resonance assignment of intrinsically disordered proteins. J. Biomol. NMR 2016, 64, 239–253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, M.; Shapiro, M.J.; Wareing, J.R. Diffusion-Edited NMR-Affinity NMR for Direct Observation of Molecular Interactions. J. Am. Chem. Soc. 1997, 119, 5249–5250. [Google Scholar] [CrossRef]
- Vega-Vázquez, M.; Cobas, J.C.; Oliveira De Sousa, F.F.; Martin-Pastor, M. A NMR reverse diffusion filter for the simplification of spectra of complex mixtures and the study of drug receptor interactions. Magn. Reson. Chem. 2011, 49, 464–468. [Google Scholar] [CrossRef]
- Carr, H.Y.; Purcell, E.M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954. [Google Scholar] [CrossRef]
- Kazimierczuk, K.; Zawadzka, A.; Koźmiński, W. Optimization of random time domain sampling in multidimensional NMR. J. Magn. Reson. 2008, 192, 123–130. [Google Scholar] [CrossRef]
- Hyberts, S.G.; Arthanari, H.; Wagner, G. Applications of non-uniform sampling and processing. Top. Curr. Chem. 2012, 316, 125–148. [Google Scholar] [CrossRef] [Green Version]
- Kazimierczuk, K.; Orekhov, V. Non-uniform sampling: Post-Fourier era of NMR data collection and processing. Magn. Reson. Chem. 2015, 53, 921–926. [Google Scholar] [CrossRef]
- Zambrello, M.A.; Craft, D.L.; Hoch, J.C.; Rovnyak, D.; Schuyler, A.D. The influence of the probability density function on spectral quality in nonuniformly sampled multidimensional NMR. J. Magn. Reson. 2020, 311, 106671. [Google Scholar] [CrossRef] [PubMed]
- Diercks, T.; Truffault, V.; Coles, M.; Millet, O. Diagonal-free 3D/4D HN,HN-trosy-noesy-trosy. J. Am. Chem. Soc. 2010, 132, 2138–2139. [Google Scholar] [CrossRef] [PubMed]
- Stanek, J.; Augustyniak, R.; Koźmiński, W. Suppression of sampling artefacts in high-resolution four-dimensional NMR spectra using signal separation algorithm. J. Magn. Reson. 2012, 214, 91–102. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Zhou, P.; Wu, J. Efficient acquisition of high-resolution 4-D diagonal-suppressed methyl-methyl NOESY for large proteins. J. Magn. Reson. 2012, 218, 128–132. [Google Scholar] [CrossRef] [Green Version]
- Stanek, J.; Nowakowski, M.; Saxena, S.; Ruszczyńska-Bartnik, K.; Ejchart, A.; Koźmiński, W. Selective diagonal-free 13 C, 13 C-edited aliphatic-aromatic NOESY experiment with non-uniform sampling. J. Biomol. NMR 2013, 56, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Werner-Allen, J.W.; Coggins, B.E.; Zhou, P. Fast acquisition of high resolution 4-D amide-amide NOESY with diagonal suppression, sparse sampling and FFT-CLEAN. J. Magn. Reson. 2010, 204, 173–178. [Google Scholar] [CrossRef] [Green Version]
- Amir, A.; Zuk, O. Bacterial community reconstruction using compressed sensing. J. Comput. Biol. 2011, 18, 1723–1741. [Google Scholar] [CrossRef]
- Morris, G.A. NMR Data Processing. Encycl. Spectrosc. Spectrom. 2017, 125–133. [Google Scholar] [CrossRef]
- Mayzel, M.; Kazimierczuk, K.; Orekhov, V.Y. The causality principle in the reconstruction of sparse NMR spectra. Chem. Commun. 2014, 50, 8947–8950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shimba, N.; Stern, A.S.; Craik, C.S.; Hoch, J.C.; Dötsch, V. Elimination of 13Cα splitting in protein NMR spectra by deconvolution with maximum entropy reconstruction. J. Am. Chem. Soc. 2003, 125, 2382–2383. [Google Scholar] [CrossRef] [PubMed]
- Kerfah, R.; Hamelin, O.; Boisbouvier, J.; Marion, D. CH3-specific NMR assignment of alanine, isoleucine, leucine and valine methyl groups in high molecular weight proteins using a single sample. J. Biomol. NMR 2015, 63, 389–402. [Google Scholar] [CrossRef] [PubMed]
- Robson, S.A.; Takeuchi, K.; Boeszoermenyi, A.; Coote, P.W.; Dubey, A.; Hyberts, S.; Wagner, G.; Arthanari, H. Mixed pyruvate labeling enables backbone resonance assignment of large proteins using a single experiment. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ottiger, M.; Delaglio, F.; Bax, A. Measurement of J and Dipolar Couplings from Simplified Two-Dimensional NMR Spectra. J. Magn. Reson. 1998, 131, 373–378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersson, P.; Weigelt, J.; Otting, G. Spin-state selection filters for the measurement of heteronuclear one-bond coupling constants. J. Biomol. NMR 1998, 12, 435–441. [Google Scholar] [CrossRef]
- Stern, A.S.; Hoch, J.C. A new approach to compressed sensing for NMR. Magn. Reson. Chem. 2015, 53, 908–912. [Google Scholar] [CrossRef]
- Jaravine, V.; Ibraghimov, I.; Orekhov, V.Y. Removal of a time barrier for high-resolution multidimensional NMR spectroscopy. Nat. Methods 2006, 3, 605–607. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Pados, D.A. Motion-aware decoding of compressed-sensed video. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 438–444. [Google Scholar] [CrossRef]
- Konar, A.S.; Aiholli, S.; Shashikala, H.C.; Babu, D.R.; Geethanath, S. Application of Region of Interest Compressed Sensing to accelerate magnetic resonance angiography. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC 2014, Chicago, IL, USA, 26–30 August 2014; pp. 2428–2431. [Google Scholar] [CrossRef]
- Kazimierczuk, K.; Zawadzka, A.; Koźmiński, W.; Zhukov, I. Lineshapes and artifacts in Multidimensional Fourier Transform of arbitrary sampled NMR data sets. J. Magn. Reson. 2007, 188, 344–356. [Google Scholar] [CrossRef]
- Mitchell, D.P. Generating antialiased images at low sampling densities. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1987, Anaheim, CA, USA, 27–31 July 1987; pp. 65–72. [Google Scholar] [CrossRef]
- Lagae, A.; Dutré, P. A comparison of methods for generating Poisson disk distributions. Comput. Graph. Forum 2008, 27, 114–129. [Google Scholar] [CrossRef] [Green Version]
- Hyberts, S.G.; Takeuchi, K.; Wagner, G. Poisson-gap sampling and forward maximum entropy reconstruction for enhancing the resolution and sensitivity of protein NMR data. J. Am. Chem. Soc. 2010, 132, 2145–2147. [Google Scholar] [CrossRef] [Green Version]
- Barna, J.C.; Laue, E.D.; Mayger, M.R.; Skilling, J.; Worrall, S.J. Exponential sampling, an alternative method for sampling in two-dimensional NMR experiments. J. Magn. Reson. (1969) 1987, 73, 69–77. [Google Scholar] [CrossRef]
- Paramasivam, S.; Suiter, C.L.; Hou, G.; Sun, S.; Palmer, M.; Hoch, J.C.; Rovnyak, D.; Polenova, T. Enhanced sensitivity by nonuniform sampling enables multidimensional MAS NMR spectroscopy of protein assemblies. J. Phys. Chem. B 2012, 116, 7416–7427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kazimierczuk, K.; Lafon, O.; Lesot, P. Criteria for sensitivity enhancement by compressed sensing: Practical application to anisotropic NAD 2D-NMR spectroscopy. Analyst 2014, 139, 2702–2713. [Google Scholar] [CrossRef] [PubMed]
- Hyberts, S.G.; Robson, S.A.; Wagner, G. Interpolating and extrapolating with hmsIST: Seeking a tmax for optimal sensitivity, resolution and frequency accuracy. J. Biomol. NMR 2017, 68, 139–154. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.E.; Redner, R.A.; Uselton, S.P. Statistically Optimized Sampling for Distributed Ray Tracing. Comput. Graph. (ACM) 1985, 19, 61–67. [Google Scholar] [CrossRef]
- Kajiya, J.T. The rendering equation. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1986, Dallas, TX, USA, 18–22 August 1986; pp. 143–150. [Google Scholar] [CrossRef]
- Gołowicz, D.; Kasprzak, P.; Orekhov, V.; Kazimierczuk, K. Fast time-resolved NMR with non-uniform sampling. Prog. Nucl. Mag. Res. Spectrosc. 2019. [Google Scholar] [CrossRef]
- Dass, R.; Kasprzak, P.; Koźmiński, W.; Kazimierczuk, K. Artifacts in time-resolved NUS: A case study of NOE build-up curves from 2D NOESY. J. Magn. Reson. 2016, 265, 108–116. [Google Scholar] [CrossRef]
- Bermel, W.; Dass, R.; Neidig, K.P.; Kazimierczuk, K. Two-Dimensional NMR Spectroscopy with Temperature-Sweep. ChemPhysChem 2014, 15, 2217–2220. [Google Scholar] [CrossRef]
- Dass, R.; Grudzia̧ż, K.; Ishikawa, T.; Nowakowski, M.; Dbowska, R.; Kazimierczuk, K. Fast 2D NMR spectroscopy for in vivo monitoring of bacterial metabolism in complex mixtures. Front. Microbiol. 2017, 8, 1306. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; D’Agostino, C.; Holland, D.J.; Gladden, L.F. In situ study of reaction kinetics using compressed sensing NMR. Chem. Commun. 2014, 50, 14137–14140. [Google Scholar] [CrossRef] [Green Version]
- Gołowicz, D.; Kazimierczuk, K.; Urbańczyk, M.; Ratajczyk, T. Monitoring Hydrogenation Reactions using Benchtop 2D NMR with Extraordinary Sensitivity and Spectral Resolution. ChemistryOpen 2019, 8, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Vasanawala, S.S.; Alley, M.T.; Hargreaves, B.A.; Barth, R.A.; Pauly, J.M.; Lustig, M. Improved pediatric MR imaging with compressed sensing. Radiology 2010, 256, 607–616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kay, L.E.; Keifer, P.; Saarinen, T. Pure absorption gradient enhanced heteronuclear single quantum correlation spectroscopy with improved sensitivity. J. Am. Chem. Soc. 1992, 114, 10663–10665. [Google Scholar] [CrossRef]
- Orekhov, V.Y.; Jaravine, V.; Mayzel, M.; Kazimierczuk, K. MddNMR—Reconstruction of NMR Spectra from NUS Signal Using MDD and CS. Available online: http://mddnmr.spektrino.com (accessed on 28 February 2020).






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gołowicz, D.; Kasprzak, P.; Kazimierczuk, K. Enhancing Compression Level for More Efficient Compressed Sensing and Other Lessons from NMR Spectroscopy. Sensors 2020, 20, 1325. https://doi.org/10.3390/s20051325
Gołowicz D, Kasprzak P, Kazimierczuk K. Enhancing Compression Level for More Efficient Compressed Sensing and Other Lessons from NMR Spectroscopy. Sensors. 2020; 20(5):1325. https://doi.org/10.3390/s20051325
Chicago/Turabian StyleGołowicz, Dariusz, Paweł Kasprzak, and Krzysztof Kazimierczuk. 2020. "Enhancing Compression Level for More Efficient Compressed Sensing and Other Lessons from NMR Spectroscopy" Sensors 20, no. 5: 1325. https://doi.org/10.3390/s20051325
APA StyleGołowicz, D., Kasprzak, P., & Kazimierczuk, K. (2020). Enhancing Compression Level for More Efficient Compressed Sensing and Other Lessons from NMR Spectroscopy. Sensors, 20(5), 1325. https://doi.org/10.3390/s20051325