Optimizing an Adaptive Neuro-Fuzzy Inference System for Spatial Prediction of Landslide Susceptibility Using Four State-of-the-art Metaheuristic Techniques
Abstract
:1. Introduction
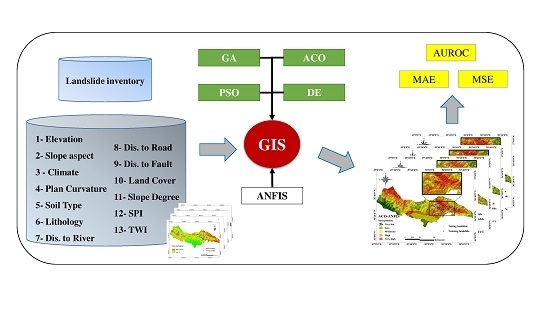
2. Materials and Methods
2.1. Study Area
2.2. Data Preparation and Spatial Relation Between the Landslide and Related Factors
2.3. Methodology
2.3.1. Adaptive Neuro-Fuzzy Inference System
2.3.2. Genetic Algorithm
2.3.3. Particle Swarm Optimization
2.3.4. Differential Evolutionary Algorithm
2.3.5. Ant Colony Optimization
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Varnes, D.; Radbruch-Hall, D. Landslides cause and effect. Bull. Int. Assoc. Eng. Geol. 1976, 13, 205–216. [Google Scholar]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Shoaei, Z.; Ghayoumian, J. The largest debris flow in the world, Seimareh Landslide, Western Iran. In Environmental Forest Science; Springer: Berlin, Germany, 1998; pp. 553–561. [Google Scholar]
- Abdullahi, S.; Mahmud, A.R.B.; Pradhan, B. Spatial modelling of site suitability assessment for hospitals using geographical information system-based multicriteria approach at Qazvin city, Iran. Geocarto Int. 2014, 29, 164–184. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A.X. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. CATENA 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Kalantar, B.; Abdullahi Mu’azu, M.; A. Rashid, A.S.; Foong, L.K.; Nguyen, H. Novel hybrids of adaptive neuro-fuzzy inference system (ANFIS) with several metaheuristic algorithms for spatial susceptibility assessment of seismic-induced landslide. Geomat. Nat. Hazards Risk 2019, 10, 1879–1911. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Moayedi, H.; Kalantar, B.; Osouli, A.; Gör, M.; Pradhan, B.; Nguyen, H.; Rashid, A.S.A. Harris hawks optimization: A novel swarm intelligence technique for spatial assessment of landslide susceptibility. Sensors 2019, 19, 3590. [Google Scholar] [CrossRef] [Green Version]
- Xiao, T.; Yin, K.; Yao, T.; Liu, S. Spatial prediction of landslide susceptibility using GIS-based statistical and machine learning models in Wanzhou County, Three Gorges Reservoir, China. Acta Geochim. 2019, 38, 654–669. [Google Scholar] [CrossRef]
- Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern Iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
- Youssef, A.M.; Al-Kathery, M.; Pradhan, B. Landslide susceptibility mapping at Al-Hasher area, Jizan (Saudi Arabia) using GIS-based frequency ratio and index of entropy models. Geosci. J. 2015, 19, 113–134. [Google Scholar] [CrossRef]
- Nicu, I.C.; Asăndulesei, A. GIS-based evaluation of diagnostic areas in landslide susceptibility analysis of Bahluieț River Basin (Moldavian Plateau, NE Romania). Are Neolithic sites in danger? Geomorphology 2018, 314, 27–41. [Google Scholar] [CrossRef]
- Fayez, L.; Pazhman, D.; Pham, B.T.; Dholakia, M.; Solanki, H.; Khalid, M.; Prakash, I. Application of Frequency Ratio Model for the Development of Landslide Susceptibility Mapping at Part of Uttarakhand State, India. Int. J. Appl. Eng. Res. 2018, 13, 6846–6854. [Google Scholar]
- Chen, W.; Chai, H.; Sun, X.; Wang, Q.; Ding, X.; Hong, H. A GIS-based comparative study of frequency ratio, statistical index and weights-of-evidence models in landslide susceptibility mapping. Arab. J. Geosci. 2016, 9, 204. [Google Scholar] [CrossRef]
- Bahrami, Y.; Hassani, H.; Maghsoudi, A. Landslide susceptibility mapping using AHP and fuzzy methods in the Gilan province, Iran. GeoJournal 2020, 1–20. [Google Scholar] [CrossRef]
- El Jazouli, A.; Barakat, A.; Khellouk, R. GIS-multicriteria evaluation using AHP for landslide susceptibility mapping in Oum Er Rbia high basin (Morocco). Geoenviron. Disasters 2019, 6, 3. [Google Scholar] [CrossRef]
- Yan, F.; Zhang, Q.; Ye, S.; Ren, B. A novel hybrid approach for landslide susceptibility mapping integrating analytical hierarchy process and normalized frequency ratio methods with the cloud model. Geomorphology 2019, 327, 170–187. [Google Scholar] [CrossRef]
- Yang, J.; Song, C.; Yang, Y.; Xu, C.; Guo, F.; Xie, L. New method for landslide susceptibility mapping supported by spatial logistic regression and GeoDetector: A case study of Duwen Highway Basin, Sichuan Province, China. Geomorphology 2019, 324, 62–71. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Z. Quantitative assessment of landslide susceptibility comparing statistical index, index of entropy, and weights of evidence in the Shangnan area, China. Entropy 2018, 20, 868. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Yang, J.; Xu, C.; Xu, C.; Song, C. Local-scale landslide susceptibility mapping using the B-GeoSVC model. Landslides 2019, 16, 1301–1312. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Regional landslide susceptibility analysis using back-propagation neural network model at Cameron Highland, Malaysia. Landslides 2010, 7, 13–30. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. A comparative study of landslide susceptibility maps produced using support vector machine with different kernel functions and entropy data mining models in China. Bull. Eng. Geol. Environ. 2018, 77, 647–664. [Google Scholar] [CrossRef]
- Vahidnia, M.H.; Alesheikh, A.A.; Alimohammadi, A.; Hosseinali, F. A GIS-based neuro-fuzzy procedure for integrating knowledge and data in landslide susceptibility mapping. Comput. Geosci. 2010, 36, 1101–1114. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Polykretis, C.; Chalkias, C.; Ferentinou, M. Adaptive neuro-fuzzy inference system (ANFIS) modeling for landslide susceptibility assessment in a Mediterranean hilly area. Bull. Eng. Geol. Environ. 2019, 78, 1173–1187. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Pham, B.T.; Shirzadi, A.; Bui, D.T.; Prakash, I.; Dholakia, M. A hybrid machine learning ensemble approach based on a radial basis function neural network and rotation forest for landslide susceptibility modeling: A case study in the Himalayan area, India. Int. J. Sediment Res. 2018, 33, 157–170. [Google Scholar] [CrossRef]
- Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Bui, D.T.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
- Li, L.; Liu, R.; Pirasteh, S.; Chen, X.; He, L.; Li, J. A novel genetic algorithm for optimization of conditioning factors in shallow translational landslides and susceptibility mapping. Arab. J. Geosci. 2017, 10, 209. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pham, B.T.; Nguyen, Q.P.; Hoang, N.-D. Spatial prediction of rainfall-induced shallow landslides using hybrid integration approach of Least-Squares Support Vector Machines and differential evolution optimization: A case study in Central Vietnam. Int. J. Digit. Earth 2016, 9, 1077–1097. [Google Scholar] [CrossRef]
- Nguyen, H.; Mehrabi, M.; Kalantar, B.; Moayedi, H.; Abdullahi, M.a.M. Potential of hybrid evolutionary approaches for assessment of geo-hazard landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2019, 10, 1667–1693. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Pourghasemi, H.R. Performance evaluation of GIS-based new ensemble data mining techniques of adaptive neuro-fuzzy inference system (ANFIS) with genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) for landslide spatial modelling. Catena 2017, 157, 310–324. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.-D.; Pham, B.; Bui, Q.-T.; Tran, C.-T.; Panahi, M.; Bin Ahamd, B. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Rostamzadeh, H.; Blaschke, T.; Gholaminia, K.; Aryal, J. A new GIS-based data mining technique using an adaptive neuro-fuzzy inference system (ANFIS) and k-fold cross-validation approach for land subsidence susceptibility mapping. Nat. Hazards 2018, 94, 497–517. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.-J.; Park, I.; Lee, S. Forecasting and validation of landslide susceptibility using an integration of frequency ratio and neuro-fuzzy models: a case study of Seorak mountain area in Korea. Environ. Earth Sci. 2015, 74, 413–429. [Google Scholar] [CrossRef]
- Ahmadlou, M.; Karimi, M.; Alizadeh, S.; Shirzadi, A.; Parvinnejhad, D.; Shahabi, H.; Panahi, M. Flood susceptibility assessment using integration of adaptive network-based fuzzy inference system (ANFIS) and biogeography-based optimization (BBO) and BAT algorithms (BA). Geocarto Int. 2018, 1–21. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-metaheuristic ensembles for spatial assessment of forest fire susceptibility. J. Environ. Manag. 2020, 109867. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Ahmad, B.B. Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. Catena 2019, 172, 212–231. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Mosallanezhad, M.; Rashid, A.S.A.; Pradhan, B. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Eng. Comput. 2019, 35, 967–984. [Google Scholar] [CrossRef]
- Shahrood (River). Available online: https://en.wikipedia.org/wiki/Shahrood_(River) (accessed on 6 March 2020).
- Shemshad, K.; Rafinejad, J.; Kamali, K.; Piazak, N.; Sedaghat, M.M.; Shemshad, M.; Biglarian, A.; Nourolahi, F.; Beigi, E.V.; Enayati, A.A. Species diversity and geographic distribution of hard ticks (Acari: Ixodoidea: Ixodidae) infesting domestic ruminants, in Qazvin Province, Iran. Parasitol. Res. 2012, 110, 373–380. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Vakhshoori, V.; Pourghasemi, H.R. A novel hybrid bivariate statistical method entitled FROC for landslide susceptibility assessment. Environ. Earth Sci. 2018, 77, 686. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S.; Buchroithner, M.F. A GIS-based back-propagation neural network model and its cross-application and validation for landslide susceptibility analyses. Comput. Environ. Urban Syst. 2010, 34, 216–235. [Google Scholar] [CrossRef]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: New tools for an old problem. Earth Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef] [Green Version]
- Pourghasemi, H.R.; Jirandeh, A.G.; Pradhan, B.; Xu, C.; Gokceoglu, C. Landslide susceptibility mapping using support vector machine and GIS at the Golestan Province, Iran. J. Earth Syst. Sci. 2013, 122, 349–369. [Google Scholar] [CrossRef] [Green Version]
- Arjmandzadeh, R.; Teshnizi, E.S.; Rastegarnia, A.; Golian, M.; Jabbari, P.; Shamsi, H.; Tavasoli, S. GIS-Based Landslide Susceptibility Mapping in Qazvin Province of Iran. Iran. J. Sci. Techno. Trans. Civil Eng. 2019, 1–29. [Google Scholar] [CrossRef]
- Oh, H.-J.; Kim, Y.-S.; Choi, J.-K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Pourghasemi, H.; Moradi, H.; Aghda, S.F. Landslide susceptibility mapping by binary logistic regression, analytical hierarchy process, and statistical index models and assessment of their performances. Nat. hazards 2013, 69, 749–779. [Google Scholar] [CrossRef]
- Moayedi, H.; Hayati, S. Modelling and optimization of ultimate bearing capacity of strip footing near a slope by soft computing methods. Appl. Soft Comput. 2018, 66, 208–219. [Google Scholar] [CrossRef]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: a case study from Kat landslides (Tokat—Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B. Novel GIS based machine learning algorithms for shallow landslide susceptibility mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kerle, N. Random forests and evidential belief function-based landslide susceptibility assessment in Western Mazandaran Province, Iran. Environ. Earth Sci. 2016, 75, 185. [Google Scholar] [CrossRef]
- Zare, M.; Pourghasemi, H.R.; Vafakhah, M.; Pradhan, B. Landslide susceptibility mapping at Vaz Watershed (Iran) using an artificial neural network model: A comparison between multilayer perceptron (MLP) and radial basic function (RBF) algorithms. Arab. J. GeoL. 2013, 6, 2873–2888. [Google Scholar] [CrossRef]
- BEVEN, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Moore, I.D.; Grayson, R.; Ladson, A. Digital terrain modelling: a review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Jang, J.-S. ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Varzandeh, M.H.M. A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Prasad, N.R.; Walker, E.A.; Walker, C.L. A First Course in Fuzzy and Neural Control; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan press Ann Arbor: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Pham, D.; Karaboga, D. Optimum design of fuzzy logic controllers using genetic algorithms. J. Syst. Eng. 1991, 1, 114–118. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 1944, pp. 1942–1948. [Google Scholar]
- Kennedy, J. Particle swarm optimization. Encycl. Mach. Learn. 2010, 760–766. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Storn, R. Differential evolution research–trends and open questions. In Advances in Differential Evolution; Springer: Berlin, Germany, 2008; pp. 1–31. [Google Scholar]
- Abdul-Rahman, O.A.; Munetomo, M.; Akama, K. An adaptive parameter binary-real coded genetic algorithm for constraint optimization problems: Performance analysis and estimation of optimal control parameters. Inf. Sci. 2013, 233, 54–86. [Google Scholar] [CrossRef]
- Zheng, Q.; Simon, D.; Richter, H.; Gao, Z. Differential particle swarm evolution for robot control tuning. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 5276–5281. [Google Scholar]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, 1992. [Google Scholar]
- Castillo, O.; Neyoy, H.; Soria, J.; Melin, P.; Valdez, F. A new approach for dynamic fuzzy logic parameter tuning in ant colony optimization and its application in fuzzy control of a mobile robot. Appl. Soft Comput. 2015, 28, 150–159. [Google Scholar] [CrossRef]
- Mahapatra, S.; Daniel, R.; Dey, D.N.; Nayak, S.K. Induction motor control using PSO-ANFIS. Procedia Comput. Sci. 2015, 48, 753–768. [Google Scholar] [CrossRef] [Green Version]
- Aghdam, I.N.; Varzandeh, M.H.M.; Pradhan, B. Landslide susceptibility mapping using an ensemble statistical index (Wi) and adaptive neuro-fuzzy inference system (ANFIS) model at Alborz Mountains (Iran). Environ. Earth Sci. 2016, 75, 553. [Google Scholar] [CrossRef]
- Pourghasemi, H.; Pradhan, B.; Gokceoglu, C.; Moezzi, K.D. A comparative assessment of prediction capabilities of Dempster–Shafer and weights-of-evidence models in landslide susceptibility mapping using GIS. Geomat. Nat. Hazards Risk 2013, 4, 93–118. [Google Scholar] [CrossRef]
- Xu, C.; Dai, F.; Xu, X.; Lee, Y.H. GIS-based support vector machine modeling of earthquake-triggered landslide susceptibility in the Jianjiang River watershed, China. Geomorphology 2012, 145, 70–80. [Google Scholar] [CrossRef]
- Egan, J.P. Signal Detection Theory and {ROC} Analysis; Academic press: Cambridge, MA, USA, 1975. [Google Scholar]
- Süzen, M.L.; Doyuran, V. Data driven bivariate landslide susceptibility assessment using geographical information systems: a method and application to Asarsuyu catchment, Turkey. Eng. Geol. 2004, 71, 303–321. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility mapping at Hoa Binh province (Vietnam) using an adaptive neuro-fuzzy inference system and GIS. Comput. Geosci. 2012, 45, 199–211. [Google Scholar]
- Sezer, E.A.; Pradhan, B.; Gokceoglu, C. Manifestation of an adaptive neuro-fuzzy model on landslide susceptibility mapping: Klang valley, Malaysia. Expert Syst. Appl. 2011, 38, 8208–8219. [Google Scholar] [CrossRef]
- Oh, H.-J.; Pradhan, B. Application of a neuro-fuzzy model to landslide-susceptibility mapping for shallow landslides in a tropical hilly area. Comput. Geosci. 2011, 37, 1264–1276. [Google Scholar] [CrossRef]
- Das, S.K.; Biswal, R.K.; Sivakugan, N.; Das, B. Classification of slopes and prediction of factor of safety using differential evolution neural networks. Environ. Earth Sci. 2011, 64, 201–210. [Google Scholar] [CrossRef]
- Termeh, S.V.R.; Kornejady, A.; Pourghasemi, H.R.; Keesstra, S. Flood susceptibility mapping using novel ensembles of adaptive neuro fuzzy inference system and metaheuristic algorithms. Sci. Total Environ. 2018, 615, 438–451. [Google Scholar] [CrossRef] [PubMed]













| Name | Symbol | Description | Geological Age | Age Era | FR |
|---|---|---|---|---|---|
| A | Qft1 | Vally terrace deposits and high level piedmont fan | Quaternary | Cenozoic | 0.1342 |
| B | Mm,s,l | Calcareous sandstone, Marl, sandy limestone, and minor conglomerate | Miocene | Cenozoic | 1.8086 |
| C | Ek | Well bedded green tuff and tuffaceous shale (KARAJ FM) | Eocene | Cenozoic | 1.8527 |
| D | Ebv | Basaltic volcanic rocks | Middle. Eocene | Cenozoic | 1.4191 |
| E | Ek.a | Calcareous shale with subordinate tuff (Asara Shale) | Middle. Eocene | Cenozoic | 0.0000 |
| F | Pr | Dark grey medium-bedded to massive limestone (RUTEH LIMESTONE) | Permian | Paleozoic | 0.9016 |
| G | TRJs | Dark grey shale and sandstone (SHEMSHAK FM.) | Triassic-Jurassic | Mesozoic | 5.8083 |
| H | Eksh | Greenish-black shale and partly tuffaceous with intercalations of tuff (Lower Shale Member) | Middle. Eocene | Cenozoic | 0.0000 |
| I | Qft2 | Low level piedment fan and vally terrace deposits | Quaternary | Cenozoic | 0.9509 |
| G | Edavt | Dacitic andesitic volcanic tuff | Middle-Late. Eocene | Cenozoic | 0.1144 |
| K | Pgkc | Light-red coarse grained, and polygenic conglomerate with sandstone intercalations | Paleocene-Eocene | Cenozoic | 1.0196 |
| L | Ogr-di | Granite to diorite | Oligocene | Cenozoic | 0.0000 |
| M | Eav | Andesitic volcanics | Middle. Eocene | Cenozoic | 0.8304 |
| N | Kbv | Basaltic volcanic | Early. Cretaceous | Mesozoic | 0.0000 |
| O | Ktzl | Thick bedded to massive, and white to pinkish orbitolina bearing limestone (TIZKUH FM) | Early. Cretaceous | Mesozoic | 0.0000 |
| P | TRe | Thick bedded grey o’olitic limestone, thin-platy, yellow to pinkish shaly limestone with worm tracks and well to thick-bedded dolomite and dolomitic limestone (ELIKAH FM.) | Early-Middle. Triassic | Mesozoic | 0.0111 |
| Q | gb | Gabbro | Eocene | Cenozoic | 5.5427 |
| R | Edav | Dacitic to Andesitic volcanic | Eocene | Cenozoic | 0.4563 |
| S | Cb | Limestone, alternation of dolomite, and verigated shale (BARUT FM) | Cambrian | Paleozoic | 0.0000 |
| T | Jl | Light grey, and thin-bedded to massive limestone (LAR FM) | Jurassic-Cretaceous | Mesozoic | 3.5884 |
| U | Edt | Rhyolitic to rhyodacitic tuff | Eocene | Cenozoic | 2.6755 |
| V | Qabv | Andesite to basaltic volcanics | Quaternary | Cenozoic | 0.2398 |
| W | Odi | Diorite | Oligocene | Cenozoic | 0.7280 |
| X | Ekgy | Gypsum | Late. Eocene | Cenozoic | 0.0000 |
| Y | Ebt | Basaltic tuff | Eocene | Cenozoic | 0.0000 |
| Susceptibility Class | GA-ANFIS | PSO-ANFIS | DE-ANFIS | ACO-ANFIS | ||||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |
| Very low | 1.51 | 0.00 | 0.91 | 0.00 | 0.00 | 0.00 | 1.16 | 0.00 |
| Low | 4.49 | 4.14 | 2.98 | 0.00 | 2.52 | 2.99 | 1.82 | 1.99 |
| Moderate | 11.85 | 10.43 | 7.40 | 0.50 | 11.43 | 7.52 | 10.10 | 4.06 |
| High | 14.03 | 9.97 | 13.67 | 1.31 | 22.37 | 19.79 | 32.92 | 33.36 |
| Very high | 68.13 | 75.46 | 75.04 | 98.19 | 63.67 | 69.71 | 54.00 | 60.58 |
| Ensemble Models | Network Results | Ranking Score | Total Ranking Score (TRS) | Rank | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training Phase | Testing Phase | Training Phase | Testing Phase | |||||||||||
| MSE | MAE | AUROC | MSE | MAE | AUROC | MSE | MAE | AUROC | MSE | MAE | AUROC | |||
| GA-ANFIS | 0.0833 | 0.1921 | 0.951 | 0.1175 | 0.2438 | 0.916 | 4 | 4 | 4 | 4 | 4 | 4 | 24 | 1 |
| PSO-ANFIS | 0.1055 | 0.2295 | 0.925 | 0.1430 | 0.2724 | 0.899 | 3 | 3 | 2 | 3 | 3 | 3 | 17 | 2 |
| DE-ANFIS | 0.1071 | 0.2476 | 0.934 | 0.1579 | 0.3128 | 0.868 | 2 | 2 | 3 | 2 | 2 | 2 | 13 | 3 |
| ACO-ANFIS | 0.1534 | 0.3335 | 0.868 | 0.1887 | 0.3755 | 0.800 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrabi, M.; Pradhan, B.; Moayedi, H.; Alamri, A. Optimizing an Adaptive Neuro-Fuzzy Inference System for Spatial Prediction of Landslide Susceptibility Using Four State-of-the-art Metaheuristic Techniques. Sensors 2020, 20, 1723. https://doi.org/10.3390/s20061723
Mehrabi M, Pradhan B, Moayedi H, Alamri A. Optimizing an Adaptive Neuro-Fuzzy Inference System for Spatial Prediction of Landslide Susceptibility Using Four State-of-the-art Metaheuristic Techniques. Sensors. 2020; 20(6):1723. https://doi.org/10.3390/s20061723
Chicago/Turabian StyleMehrabi, Mohammad, Biswajeet Pradhan, Hossein Moayedi, and Abdullah Alamri. 2020. "Optimizing an Adaptive Neuro-Fuzzy Inference System for Spatial Prediction of Landslide Susceptibility Using Four State-of-the-art Metaheuristic Techniques" Sensors 20, no. 6: 1723. https://doi.org/10.3390/s20061723
APA StyleMehrabi, M., Pradhan, B., Moayedi, H., & Alamri, A. (2020). Optimizing an Adaptive Neuro-Fuzzy Inference System for Spatial Prediction of Landslide Susceptibility Using Four State-of-the-art Metaheuristic Techniques. Sensors, 20(6), 1723. https://doi.org/10.3390/s20061723