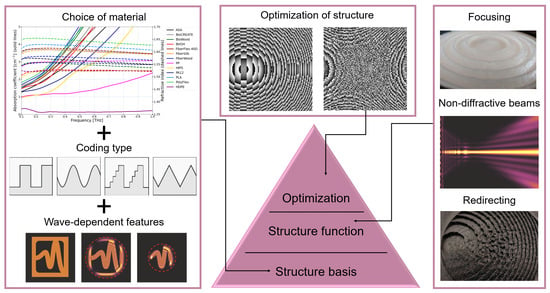
The Magic of Optics—An Overview of Recent Advanced Terahertz Diffractive Optical Elements
Abstract
:1. Introduction
2. Characteristic Features Concerning Manufacturing
3. Classic DOE Design
4. Features of THz Design
- Zone very close to the aperture— and propagation is described by Rayleigh-Sommerfeld integral;
- Non-paraxial zone— and and propagation is described by Sommerfeld integral;
- Paraxial Fresnel zone (near-field)— where the paraxial Fresnel integral is used;
- Fraunhofer zone (far-field)— and propagation is described by Fraunhofer integral.
5. Efficient Focusing of THz Radiation
6. Non-Diffractive Beams
7. Redirecting of Incident Radiation
8. Optimization Algorithms and Neural Network Approach
9. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siemion, A.; Siemion, A.; Makowski, M.; Suszek, J.; Bomba, J.; Czerwiński, A.; Garet, F.; Coutaz, J.L.; Sypek, M. Diffractive paper lens for terahertz optics. Opt. Lett. 2012, 37, 4320–4322. [Google Scholar] [CrossRef] [PubMed]
- Rachon, M.; Liebert, K.; But, D.; Zagrajek, P.; Siemion, A.; Kolodziejczyk, A.; Sypek, M.; Suszek, J. Enhanced Sub-wavelength Focusing by Double-Sided Lens with Phase Correction in THz Range. J. Infrared Millim. Terahertz Waves 2020. [Google Scholar] [CrossRef]
- Minkevičius, L.; Indrišiūnas, S.; Šniaukas, R.; Voisiat, B.; Janonis, V.; Tamošiūnas, V.; Kašalynas, I.; Račiukaitis, G.; Valušis, G. Terahertz multilevel phase Fresnel lenses fabricated by laser patterning of silicon. Opt. Lett. 2017, 42, 1875–1878. [Google Scholar] [CrossRef] [PubMed]
- Busch, S.F.; Weidenbach, M.; Balzer, J.C.; Koch, M. THz optics 3D printed with TOPAS. J. Infrared Millim. Terahertz Waves 2016, 37, 303–307. [Google Scholar] [CrossRef]
- Liebert, K.; Rachon, M.; Siemion, A.; Suszek, J.; But, D.; Knap, W.; Sypek, M. THz beam shaper realizing fan-out patterns. J. Infrared Millim. Terahertz Waves 2017, 38, 1019–1030. [Google Scholar] [CrossRef] [Green Version]
- Siemion, A.; Komorowski, P.; Surma, M.; Ducin, I.; Sobotka, P.; Walczakowski, M.; Czerwińska, E. Terahertz diffractive structures for compact in-reflection inspection setup. Opt. Express 2020, 28, 715–723. [Google Scholar] [CrossRef]
- Hampel, B.; Tollkühn, M.; Elenskiy, I.; Martens, M.; Kajevic, D.; Schilling, M. Josephson Cantilevers for THz Microscopy of Additive Manufactured Diffractive Optical Components. IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
- Firoozabadi, S.; Beltran-Mejia, F.; Soltani, A.; Jahn, D.; Busch, S.; Balzer, J.; Koch, M. THz transmission blazed grating made out of paper tissue. In Proceedings of the 2017 42nd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Cancun, Mexico, 27 August–1 September 2017; pp. 1–2. [Google Scholar]
- Siemion, A.; Siemion, A.; Suszek, J.; Kowalczyk, A.; Bomba, J.; Sobczyk, A.; Palka, N.; Zagrajek, P.; Kolodziejczyk, A.; Sypek, M. THz beam shaping based on paper diffractive optics. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 568–575. [Google Scholar] [CrossRef]
- Surma, M.; Ducin, I.; Zagrajek, P.; Siemion, A. Sub-Terahertz Computer Generated Hologram with Two Image Planes. Appl. Sci. 2019, 9, 659. [Google Scholar] [CrossRef] [Green Version]
- Gospodaric, J.; Kuzmenko, A.; Pimenov, A.; Huber, C.; Suess, D.; Rotter, S.; Pimenov, A. 3D-printed phase waveplates for THz beam shaping. Appl. Phys. Lett. 2018, 112, 221104. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Liu, J.; Niu, L.; Wei, X.; Wang, K.; Yang, Z. Terahertz circular Airy vortex beams. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.; Chen, H.T. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neu, J.; Beigang, R.; Rahm, M. Metamaterial-based gradient index beam steerers for terahertz radiation. Appl. Phys. Lett. 2013, 103, 041109. [Google Scholar] [CrossRef]
- Hu, D.; Moreno, G.; Wang, X.; He, J.; Chahadih, A.; Xie, Z.; Wang, B.; Akalin, T.; Zhang, Y. Dispersion characteristic of ultrathin terahertz planar lenses based on metasurface. Opt. Commun. 2014, 322, 164–168. [Google Scholar] [CrossRef]
- Headland, D.; Carrasco, E.; Nirantar, S.; Withayachumnankul, W.; Gutruf, P.; Schwarz, J.; Abbott, D.; Bhaskaran, M.; Sriram, S.; Perruisseau-Carrier, J.; et al. Dielectric resonator reflectarray as high-efficiency nonuniform terahertz metasurface. ACS Photonics 2016, 3, 1019–1026. [Google Scholar] [CrossRef]
- Chang, C.C.; Headland, D.; Abbott, D.; Withayachumnankul, W.; Chen, H.T. Demonstration of a highly efficient terahertz flat lens employing tri-layer metasurfaces. Opt. Lett. 2017, 42, 1867–1870. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, H.; Li, Z.; Yuan, H.; Cao, L.; Luo, Z.; Zhang, K.; Zhang, Z.; Wen, Z.; Zhu, L.G.; et al. All-dielectric metalens for terahertz wave imaging. Opt. Express 2018, 26, 14132–14142. [Google Scholar] [CrossRef]
- Headland, D.; Monnai, Y.; Abbott, D.; Fumeaux, C.; Withayachumnankul, W. Tutorial: Terahertz beamforming, from concepts to realizations. APL Photonics 2018, 3, 051101. [Google Scholar] [CrossRef] [Green Version]
- Headland, D.; Niu, T.; Carrasco, E.; Abbott, D.; Sriram, S.; Bhaskaran, M.; Fumeaux, C.; Withayachumnankul, W. Terahertz reflectarrays and nonuniform metasurfaces. IEEE J. Sel. Top. Quantum Electron. 2016, 23, 1–18. [Google Scholar] [CrossRef]
- Siemion, A. Terahertz Diffractive Optics—Smart Control over Radiation. J. Infrared Millim. Terahertz Waves 2019, 40, 477–499. [Google Scholar] [CrossRef] [Green Version]
- Anderson, E.H. Specialized electron beam nanolithography for EUV and X-ray diffractive optics. IEEE J. Quantum Electron. 2005, 42, 27–35. [Google Scholar] [CrossRef]
- Deuter, V.; Grochowicz, M.; Brose, S.; Biller, J.; Danylyuk, S.; Taubner, T.; Siemion, A.; Grützmacher, D.; Juschkin, L. Computational proximity lithography with extreme ultraviolet radiation. Opt. Express 2020, 28, 27000–27012. [Google Scholar] [CrossRef] [PubMed]
- Naulleau, P.P.; Liddle, J.A.; Salmassi, F.; Anderson, E.H.; Gullikson, E.M. Design and fabrication of advanced EUV diffractive elements. In Micromachining Technology for Micro-Optics and Nano-Optics II; International Society for Optics and Photonics: Bellingham, WA, USA, 2003; Volume 5347, pp. 9–17. [Google Scholar]
- Braun, S.; Leson, A. Optical Elements for EUV Lithography and X-ray Optics. In Nanoscale Multifunctional Materials; Wiley-VCH Verlag GmbH & Co. KGaA: Hoboken, NJ, USA, 2015. [Google Scholar]
- Barton, K.; Freeman, M.; Woodward, E.; Buckley, R. Diffractive bifocal contact lenses in aphakia and pseudophakia. Eye 1991, 5, 344–347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, F.; Sugar, A.; Jacobsen, G.; Collins, M. Visual function and patient satisfaction: Comparison between bilateral diffractive multifocal intraocular lenses and monovision pseudophakia. J. Cataract Refract. Surg. 2011, 37, 446–453. [Google Scholar] [CrossRef] [PubMed]
- Brunner, R. Transferring diffractive optics from research to commercial applications: Part II–size estimations for selected markets. Adv. Opt. Technol. 2014, 3, 121–128. [Google Scholar] [CrossRef] [Green Version]
- Knox, W.H. Inventing a New Way to See Clearly: Non-invasive Vision Correction with Femtosecond Lasers. Technol. Innov. 2019, 20, 385–398. [Google Scholar] [CrossRef]
- Sohn, J.S.; Lee, M.B.; Kim, W.C.; Cho, E.H.; Kim, T.W.; Yoon, C.Y.; Park, N.C.; Park, Y.P. Design and fabrication of diffractive optical elements by use of gray-scale photolithography. Appl. Opt. 2005, 44, 506–511. [Google Scholar] [CrossRef]
- Aguilera, J.; Aguilera, J.; Baumeister, P.; Bloom, A.; Coursen, D.; Dobrowolski, J.; Goldstein, F.T.; Gustafson, D.E.; Kemp, R. Antireflection coatings for germanium IR optics: A comparison of numerical design methods. Appl. Opt. 1988, 27, 2832–2840. [Google Scholar] [CrossRef]
- Dobrowolski, J.; Ho, F. High performance step-down AR coatings for high refractive-index IR materials. Appl. Opt. 1982, 21, 288–292. [Google Scholar] [CrossRef]
- Lee, Y.S. Principles of Terahertz Science and Technology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 170. [Google Scholar]
- Han, D.; Lee, K.; Lim, J.; Hong, S.S.; Kim, Y.K.; Ahn, J. Terahertz lens made out of natural stone. Appl. Opt. 2013, 52, 8670–8675. [Google Scholar] [CrossRef] [Green Version]
- Sterczewski, L.A.; Grzelczak, M.; Nowak, K.; Plinski, E.F. Cast terahertz lenses made of caramelized sucrose. Opt. Eng. 2016, 55, 090505. [Google Scholar] [CrossRef]
- Siemion, A.; Surma, M.; Komorowski, P.; Ducin, I.; Sobotka, P. Terahertz diffractive optics: Different way of thinking. In Terahertz Emitters, Receivers, and Applications XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11499, p. 114990C. [Google Scholar]
- Squires, A.; Lewis, R. Feasibility and characterization of common and exotic filaments for use in 3D printed terahertz devices. J. Infrared Millim. Terahertz Waves 2018, 39, 614–635. [Google Scholar] [CrossRef] [Green Version]
- Castro-Camus, E.; Koch, M.; Hernandez-Serrano, A.I. Additive manufacture of photonic components for the terahertz band. J. Appl. Phys. 2020, 127, 210901. [Google Scholar] [CrossRef]
- Duvillaret, L.; Garet, F.; Coutaz, J.L. A reliable method for extraction of material parameters in terahertz time-domain spectroscopy. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 739–746. [Google Scholar] [CrossRef] [Green Version]
- Duvillaret, L.; Garet, F.; Coutaz, J.L. Highly precise determination of optical constants and sample thickness in terahertz time-domain spectroscopy. Appl. Opt. 1999, 38, 409–415. [Google Scholar] [CrossRef]
- Dorney, T.D.; Baraniuk, R.G.; Mittleman, D.M. Material parameter estimation with terahertz time-domain spectroscopy. JOSA A 2001, 18, 1562–1571. [Google Scholar] [CrossRef] [Green Version]
- Siemion, A.; Kostrowiecki-Lopata, P.; Pindur, A.; Zagrajek, P.; Sypek, M. Paper on designing costless THz paper optics. Adv. Mater. Sci. Eng. 2016, 2016. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Guo, Y.X.; Zirath, H.; Zhang, Y.P. Investigation on 3-D-printing technologies for millimeter-wave and terahertz applications. Proc. IEEE 2017, 105, 723–736. [Google Scholar] [CrossRef]
- Dilberoglu, U.M.; Gharehpapagh, B.; Yaman, U.; Dolen, M. The role of additive manufacturing in the era of industry 4.0. Procedia Manuf. 2017, 11, 545–554. [Google Scholar] [CrossRef]
- Low, Z.X.; Chua, Y.T.; Ray, B.M.; Mattia, D.; Metcalfe, I.S.; Patterson, D.A. Perspective on 3D printing of separation membranes and comparison to related unconventional fabrication techniques. J. Membr. Sci. 2017, 523, 596–613. [Google Scholar] [CrossRef] [Green Version]
- Fullager, D.B.; Park, S.; Hovis, C.; Li, Y.; Reese, J.; Sharma, E.; Lee, S.; Evans, C.; Boreman, G.D.; Hofmann, T. Metalized Poly-methacrylate Off-Axis Parabolic Mirrors for Terahertz Imaging Fabricated by Additive Manufacturing. J. Infrared Millim. Terahertz Waves 2019, 40, 269–275. [Google Scholar] [CrossRef]
- Walsby, E.; Wang, S.; Xu, J.; Yuan, T.; Blaikie, R.; Durbin, S.; Zhang, X.C.; Cumming, D. Multilevel silicon diffractive optics for terahertz waves. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2002, 20, 2780–2783. [Google Scholar] [CrossRef] [Green Version]
- Komlenok, M.S.; Volodkin, B.O.; Knyazev, B.A.; Kononenko, T.; Kononenko, V.; Konov, V.I.; Soifer, V.; Pavel’ev, V.; Tukmakov, K.N.; Choporova, Y.Y. Fabrication of a multilevel THz Fresnel lens by femtosecond laser ablation. Quantum Electron. 2015, 45, 933. [Google Scholar] [CrossRef]
- Indrišiūnas, S.; Richter, H.; Grigelionis, I.; Janonis, V.; Minkevičius, L.; Valušis, G.; Račiukaitis, G.; Hagelschuer, T.; Hübers, H.W.; Kašalynas, I. Laser-processed diffractive lenses for the frequency range of 4.7 THz. Opt. Lett. 2019, 44, 1210–1213. [Google Scholar] [CrossRef]
- Gatesman, A.; Waldman, J.; Ji, M.; Musante, C.; Yagvesson, S. An anti-reflection coating for silicon optics at terahertz frequencies. IEEE Microw. Guid. Wave Lett. 2000, 10, 264–266. [Google Scholar] [CrossRef]
- Tamošiūnaitė, M.; Indrišiūnas, S.; Tamošiūnas, V.; Minkevičius, L.; Urbanowicz, A.; Račiukaitis, G.; Kašalynas, I.; Valušis, G. Focusing of terahertz radiation with laser-ablated antireflective structures. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 541–548. [Google Scholar] [CrossRef]
- Marron, J.C.; Angell, D.K.; Tai, A.M. Higher-order kinoforms. In Computer and Optically Formed Holographic Optics; International Society for Optics and Photonics: Bellingham, WA, USA, 1990; Volume 1211, pp. 62–66. [Google Scholar]
- Middendorf, J.; LeMaster, D.; Zarepoor, M.; Brown, E. Design of multi-order diffractive THz lenses. In Proceedings of the 2012 37th International Conference on Infrared, Millimeter, and Terahertz Waves, Wollongong, Australia, 23–28 September 2012; pp. 1–2. [Google Scholar]
- Suszek, J.; Siemion, A.; Błocki, N.; Makowski, M.; Czerwiński, A.; Bomba, J.; Kowalczyk, A.; Ducin, I.; Kakarenko, K.; Pałka, N.; et al. High order kinoforms as a broadband achromatic diffractive optics for terahertz beams. Opt. Express 2014, 22, 3137–3144. [Google Scholar] [CrossRef]
- Headland, D.; Withayachumnankul, W.; Webb, M.; Ebendorff-Heidepriem, H.; Luiten, A.; Abbott, D. Analysis of 3D-printed metal for rapid-prototyped reflective terahertz optics. Opt. Express 2016, 24, 17384–17396. [Google Scholar] [CrossRef] [Green Version]
- Surma, M.; Ducin, I.; Sypek, M.; Zagrajek, P.; Siemion, A. Optimization of THz diffractive optical elements thickness. Photonics Lett. Pol. 2018, 10, 115–117. [Google Scholar] [CrossRef]
- Soifer, V.A.; Kotlar, V.; Doskolovich, L. Iteractive Methods for Diffractive Optical Elements Computation; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- O’Shea, D.C.; Suleski, T.J.; Kathman, A.D.; Prather, D.W. Diffractive Optics: Design, Fabrication, and Test; SPIE Press: Bellingham, WA, USA, 2004; Volume 62. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics; Roberts and Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Del Mar Sánchez-López, M.; Moreno, I.; Martínez-García, A. Teaching diffraction gratings by means of a phasor analysis. In Education and Training in Optics and Photonics; Optical Society of America: Washington, DC, USA, 2009; p. EMA1. [Google Scholar]
- Minin, I.V.; Minin, O.V. Diffractional Optics of Millimetre Waves; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Wyrowski, F. Diffractive optical elements: Iterative calculation of quantized, blazed phase structures. JOSA A 1990, 7, 961–969. [Google Scholar] [CrossRef]
- Taghizadeh, M.R.; Blair, P.; Layet, B.; Barton, I.; Waddie, A.; Ross, N. Design and fabrication of diffractive optical elements. Microelectron. Eng. 1997, 34, 219–242. [Google Scholar] [CrossRef]
- Jiménez, J.; Anera, R.; Jiménez del Barco, L.; Hita, E. Effect on laser-ablation algorithms of reflection losses and nonnormal incidence on the anterior cornea. Appl. Phys. Lett. 2002, 81, 1521–1523. [Google Scholar] [CrossRef] [Green Version]
- Suszek, J.; Sypek, M.; Makowski, M.; Garet, F.; Ducin, I.; Kakarenko, K.; Bomba, J.; Coutaz, J.L. Evaluation of the shadow effect in terahertz kinoform gratings. Opt. Lett. 2013, 38, 1464–1466. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Xiang, F.; You, C.; Wang, K.; Yang, Z.; Liu, J.; Wang, S. Generation of a terahertz collimated top-hat beam by using two thin diffractive phase plates. OSA Contin. 2018, 1, 1341–1348. [Google Scholar] [CrossRef]
- Kašalynas, I.; Venckevičius, R.; Minkevičius, L.; Sešek, A.; Wahaia, F.; Tamošiūnas, V.; Voisiat, B.; Seliuta, D.; Valušis, G.; Švigelj, A.; et al. Spectroscopic terahertz imaging at room temperature employing microbolometer terahertz sensors and its application to the study of carcinoma tissues. Sensors 2016, 16, 432. [Google Scholar] [CrossRef]
- Voisiat, B.; Indrišiūnas, S.; Šniaukas, R.; Minkevičius, L.; Kašalynas, I.; Račiukaitis, G. Laser processing for precise fabrication of the THz optics. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXII; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10091, p. 100910F. [Google Scholar]
- Pavelyev, V.; Komlenok, M.; Volodkin, B.; Knyazev, B.; Kononenko, T.; Konov, V.; Soifer, V.; Choporova, Y.Y. Fabrication of high-effective silicon diffractive optics for the terahertz range by femtosecond laser ablation. Phys. Procedia 2016, 84, 170–174. [Google Scholar] [CrossRef]
- Minkevičius, L.; Indrišiūnas, S.; Šniaukas, R.; Račiukaitis, G.; Janonis, V.; Tamošiūnas, V.; Kašalynas, I.; Valušis, G. Compact diffractive optics for THz imaging. Lith. J. Phys. 2018, 58. [Google Scholar] [CrossRef] [Green Version]
- Kononenko, T.V.; Knyazev, B.A.; Sovyk, D.N.; Pavelyev, V.S.; Komlenok, M.S.; Komandin, G.A.; Konov, V.I. Silicon kinoform cylindrical lens with low surface roughness for high-power terahertz radiation. Opt. Laser Technol. 2020, 123, 105953. [Google Scholar] [CrossRef]
- Tofani, S.; Zografopoulos, D.C.; Missori, M.; Fastampa, R.; Beccherelli, R. Terahertz focusing properties of polymeric zone plates characterized by a modified knife-edge technique. JOSA B 2019, 36, D88–D96. [Google Scholar] [CrossRef]
- Shang, Y.; Wang, X.; Sun, W.; Han, P.; Ye, J.; Feng, S.; Zhang, Y. Terahertz image reconstruction based on compressed sensing and inverse Fresnel diffraction. Opt. Express 2019, 27, 14725–14735. [Google Scholar] [CrossRef]
- Rachon, M.; Liebert, K.; Siemion, A.; Bomba, J.; Sobczyk, A.; Knap, W.; Coquillat, D.; Suszek, J.; Sypek, M. Geometrical aberration suppression for large aperture sub-THz lenses. J. Infrared Millim. Terahertz Waves 2017, 38, 347–355. [Google Scholar] [CrossRef] [Green Version]
- Machado, F.; Zagrajek, P.; Monsoriu, J.A.; Furlan, W.D. Terahertz sieves. IEEE Trans. Terahertz Sci. Technol. 2017, 8, 140–143. [Google Scholar] [CrossRef]
- Zhao, F.; Li, Z.; Dai, X.; Liao, X.; Li, S.; Cao, J.; Shang, Z.; Zhang, Z.; Liang, G.; Chen, G.; et al. Broadband Achromatic Sub-Diffraction Focusing by an Amplitude-Modulated Terahertz Metalens. Adv. Opt. Mater. 2020, 8, 2000842. [Google Scholar] [CrossRef]
- Yang, M.; Ruan, D.; Du, L.; Qin, C.; Li, Z.; Lin, C.; Chen, G.; Wen, Z. Subdiffraction focusing of total electric fields of terahertz wave. Opt. Commun. 2020, 458, 124764. [Google Scholar] [CrossRef]
- Iba, A.; Domier, C.W.; Ikeda, M.; Mase, A.; Pham, A.V.; Luhmann, N.C. Realizing sub-diffraction focusing for terahertz. In Proceedings of the 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Paris, France, 1–6 September 2019; pp. 1–2. [Google Scholar]
- Furlan, W.D.; Ferrando, V.; Monsoriu, J.A.; Zagrajek, P.; Czerwińska, E.; Szustakowski, M. 3D printed diffractive terahertz lenses. Opt. Lett. 2016, 41, 1748–1751. [Google Scholar] [CrossRef] [PubMed]
- Jokubauskis, D.; Minkevičius, L.; Karaliūnas, M.; Indrišiūnas, S.; Kašalynas, I.; Račiukaitis, G.; Valušis, G. Fibonacci terahertz imaging by silicon diffractive optics. Opt. Lett. 2018, 43, 2795–2798. [Google Scholar] [CrossRef] [PubMed]
- Monsoriu, J.; Calatayud, A.; Remón, L.; Furlan, W.D.; Saavedra, G.; Andrés, P. Bifocal Fibonacci diffractive lenses. IEEE Photonics J. 2013, 5, 3400106. [Google Scholar] [CrossRef]
- Jaroszewicz, Z.; Kolodziejczyk, A.; Sypek, M.; Gomez-Reino, C. Non-paraxial analytical solution for the generation of focal curves. J. Mod. Opt. 1996, 43, 617–637. [Google Scholar] [CrossRef]
- Szkudlarek, K.; Sypek, M.; Cywiński, G.; Suszek, J.; Zagrajek, P.; Feduniewicz-Żmuda, A.; Yahniuk, I.; Yatsunenko, S.; Nowakowska-Siwińska, A.; Coquillat, D.; et al. Terahertz 3D printed diffractive lens matrices for field-effect transistor detector focal plane arrays. Opt. Express 2016, 24, 20119–20131. [Google Scholar] [CrossRef] [Green Version]
- Liebert, K.; Rachoń, M.; Bomba, J.; Sobczyk, A.; Zagrajek, P.; Sypek, M.; Suszek, J.; Siemion, A. THz diffractive focusing structures for broadband application. Photonics Lett. Pol. 2018, 10, 76–78. [Google Scholar] [CrossRef]
- Liebert, K.; Rachon, M.; Kolodziejczyk, A.; Sypek, M.; Ducin, I.; Zagrajek, P.; Siemion, A. Study of thin, achromatic diffractive structures to focus terahertz radiation on a detector. Opt. Appl. 2020, 50, 463–476. [Google Scholar]
- He, J.; Ye, J.; Wang, X.; Kan, Q.; Zhang, Y. A broadband terahertz ultrathin multi-focus lens. Sci. Rep. 2016, 6, 28800. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Yan, X.; Liang, L.; Wei, D.; Wang, M.; Wang, Y.; Yao, J. The novel hybrid metal-graphene metasurfaces for broadband focusing and beam-steering in farfield at the terahertz frequencies. Carbon 2018, 132, 529–538. [Google Scholar] [CrossRef]
- Pakhomov, A.; Arkhipov, R.; Arkhipov, M.; Demircan, A.; Morgner, U.; Rosanov, N.; Babushkin, I. Unusual terahertz waveforms from a resonant medium controlled by diffractive optical elements. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Zhang, H.; Wang, K. Diffraction-free THz sheet and its application on THz imaging system. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 471–475. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.; Chávez-Cerda, S. Alternative formulation for invariant optical fields: Mathieu beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef] [PubMed]
- Bouchal, Z. Composition of the angular spectrum of the pseudo-nondiffracting beams. Opt. Commun. 2001, 197, 23–35. [Google Scholar] [CrossRef]
- Liu, C.; Niu, L.; Wang, K.; Liu, J. 3D-printed diffractive elements induced accelerating terahertz Airy beam. Opt. Express 2016, 24, 29342–29348. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, B.; Ba, Z.; Ni, S.; Cao, J.; Wang, X. Generation of Broadband THz Airy Beams Applying 3D Printing Technique. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–3. [Google Scholar]
- Minkevičius, L.; Jokubauskis, D.; Kašalynas, I.; Orlov, S.; Urbas, A.; Valušis, G. Bessel terahertz imaging with enhanced contrast realized by silicon multi-phase diffractive optics. Opt. Express 2019, 27, 36358–36367. [Google Scholar] [CrossRef]
- Niu, L.; Wang, K.; Yang, Y.; Wu, Q.; Ye, X.; Yang, Z.; Liu, J.; Yu, H. Diffractive elements for zero-order Bessel beam generation with application in the terahertz reflection imaging. IEEE Photonics J. 2018, 11, 1–12. [Google Scholar] [CrossRef]
- Wu, G.B.; Chan, K.F.; Chan, C.H. 3-D Printed Terahertz Lens to Generate Higher-Order Bessel Beams Carrying OAM. In IEEE Transactions on Antennas and Propagation; IEEE: New York, NY, USA, 2020. [Google Scholar]
- Choporova, Y.Y.; Knyazev, B.; Kulipanov, G.; Pavelyev, V.; Scheglov, M.; Vinokurov, N.; Volodkin, B.; Zhabin, V. High-power Bessel beams with orbital angular momentum in the terahertz range. Phys. Rev. A 2017, 96, 023846. [Google Scholar] [CrossRef]
- Volodkin, B.; Choporova, Y.; Knyazev, B.; Kulipanov, G.; Pavelyev, V.; Soifer, V.; Vinokurov, N. Fabrication and characterization of diffractive phase plates for forming high-power terahertz vortex beams using free electron laser radiation. Opt. Quantum Electron. 2016, 48, 223. [Google Scholar] [CrossRef]
- Yang, Y.; Ye, X.; Niu, L.; Wang, K.; Yang, Z.; Liu, J. Generating terahertz perfect optical vortex beams by diffractive elements. Opt. Express 2020, 28, 1417–1425. [Google Scholar] [CrossRef] [PubMed]
- Machado, F.; Zagrajek, P.; Ferrando, V.; Monsoriu, J.A.; Furlan, W.D. Multiplexing THz Vortex Beams With a Single Diffractive 3-D Printed Lens. IEEE Trans. Terahertz Sci. Technol. 2018, 9, 63–66. [Google Scholar] [CrossRef]
- Liu, C.; Wei, X.; Niu, L.; Wang, K.; Yang, Z.; Liu, J. Discrimination of orbital angular momentum modes of the terahertz vortex beam using a diffractive mode transformer. Opt. Express 2016, 24, 12534–12541. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.J.; Huang, J.G.; Xiao, Z.Y.; Huang, Z.M.; Shu, R.; He, Z.P. Terahertz dispersion using multi-depth phase modulation grating. Opt. Express 2019, 27, 12732–12747. [Google Scholar] [CrossRef]
- Seifert, J.M.; Hernandez-Cardoso, G.G.; Koch, M.; Castro-Camus, E. Terahertz beam steering using active diffraction grating fabricated by 3D printing. Opt. Express 2020, 28, 21737–21744. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Fan, Q.P.; Zhang, Q.Q.; Wei, L.; Chen, Y.; Yang, Z.H.; Cao, L.F. High efficiency terahertz diffraction grating with trapezoidal elements. Chin. Phys. B 2017, 26, 124203. [Google Scholar] [CrossRef]
- Mirzaei, B.; Silva, J.; Luo, Y.; Liu, X.; Wei, L.; Hayton, D.J.; Gao, J.; Groppi, C. Efficiency of multi-beam Fourier phase gratings at 1.4 THz. Opt. Express 2017, 25, 6581–6588. [Google Scholar] [CrossRef] [Green Version]
- Dammann, H.; Görtler, K. High-efficiency in-line multiple imaging by means of multiple phase holograms. Opt. Commun. 1971, 3, 312–315. [Google Scholar] [CrossRef]
- Dammann, H.; Klotz, E. Coherent optical generation and inspection of two-dimensional periodic structures. Opt. Acta: Int. J. Opt. 1977, 24, 505–515. [Google Scholar] [CrossRef]
- Nadell, C.; Fan, K.; Padilla, W. Resonance-domain diffractive lens for the terahertz region. Opt. Lett. 2018, 43, 2384–2387. [Google Scholar] [CrossRef] [PubMed]
- Banerji, S.; Chanana, A.; Condori-Quispe, H.O.; Arezoomandan, S.; Nahata, A.; Sensale-Rodriguez, B. Demonstration of computational THz diffractive optical elements enabled by a modified direct binary search technique. In Proceedings of the 2018 43rd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Chengdu, China, 29 August–3 September 2018; pp. 1–3. [Google Scholar]
- Banerji, S.; Sensale-Rodriguez, B. 3D-printed diffractive terahertz optical elements through computational design. In Micro-and Nanotechnology Sensors, Systems, and Applications XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10982, p. 109822X. [Google Scholar]
- Banerji, S.; Chanana, A.; Condori, H.; Nahata, A.; Sensale-Rodriguez, B. Efficient Design of Diffractive THz Lenses for Aberration Rectified Focusing via Modified Binary Search Algorithm. In CLEO: QELS_Fundamental Science; Optical Society of America: Washington, DC, USA, 2018; p. JW2A-76. [Google Scholar]
- Banerji, S.; Sensale-Rodriguez, B. A computational design framework for efficient, fabrication error-tolerant, planar THz diffractive optical elements. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, Y.; Mengu, D.; Yardimci, N.T.; Rivenson, Y.; Veli, M.; Jarrahi, M.; Ozcan, A. Design of task-specific optical systems using broadband diffractive neural networks. Light. Sci. Appl. 2019, 8, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Liao, D.; Chan, K.F.; Chan, C.H.; Zhang, Q.; Wang, H. All-optical diffractive neural networked terahertz hologram. Opt. Lett. 2020, 45, 2906–2909. [Google Scholar] [CrossRef]









| Phase Coding Method | ||
|---|---|---|
| Kinoform (1st order) | ||
| Kinoform ( order) | ||
| Phase N-level | up to | |
| Phase 16-level | ||
| Phase 8-level | ||
| Phase 4-level | ||
| Phase binary (2-level—with fill factor a) | up to | |
| Phase sinusoidal * | up to | |
| Amplitude binary (with fill factor a) | up to | |
| Amplitude sinusoidal ** | up to |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siemion, A. The Magic of Optics—An Overview of Recent Advanced Terahertz Diffractive Optical Elements. Sensors 2021, 21, 100. https://doi.org/10.3390/s21010100
Siemion A. The Magic of Optics—An Overview of Recent Advanced Terahertz Diffractive Optical Elements. Sensors. 2021; 21(1):100. https://doi.org/10.3390/s21010100
Chicago/Turabian StyleSiemion, Agnieszka. 2021. "The Magic of Optics—An Overview of Recent Advanced Terahertz Diffractive Optical Elements" Sensors 21, no. 1: 100. https://doi.org/10.3390/s21010100
APA StyleSiemion, A. (2021). The Magic of Optics—An Overview of Recent Advanced Terahertz Diffractive Optical Elements. Sensors, 21(1), 100. https://doi.org/10.3390/s21010100