Temporal Convolutional Neural Networks for Radar Micro-Doppler Based Gait Recognition †
Abstract
:1. Introduction
2. Related Work
3. The Proposed Methodology
3.1. Gait MD Feature Model
- is the backscattering coefficient;
- is the carrier wavelength;
- , with , is the range function varying with time due to micro-motion.
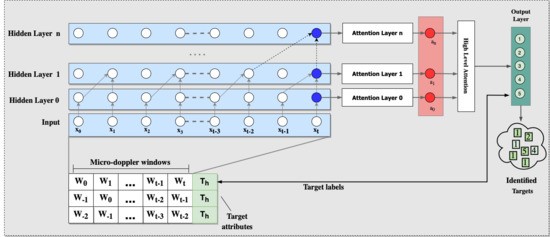
3.2. The TCN Classifier
4. Validation and Assessment
4.1. Dataset Construction
4.2. Experimental Settings
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saponara, S.; Neri, B. Radar Sensor Signal Acquisition and Multidimensional FFT Processing for Surveillance Applications in Transport Systems. IEEE Trans. Instrum. Meas. 2017, 66, 604–615. [Google Scholar] [CrossRef]
- Kim, B.s.; Jin, Y.; Kim, S.; Lee, J. A Low-Complexity FMCW Surveillance Radar Algorithm Using Two Random Beat Signals. Sensors 2019, 19, 608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Björklund, S.; Johansson, T.; Petersson, H. Evaluation of a micro-Doppler classification method on mm-wave data. In Proceedings of the 2012 IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012; pp. 934–939. [Google Scholar] [CrossRef]
- Izzo, A.; Ausiello, L.; Clemente, C.; Soraghan, J.J. Loudspeaker Analysis: A Radar Based Approach. IEEE Sens. J. 2020, 20, 1223–1237. [Google Scholar] [CrossRef] [Green Version]
- Chen, V.C.; Li, F.; Ho, S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model, and simulation study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Chen, V. The Micro-Doppler Effect in Radar, 2nd ed.; Artech House: Norwood, MA, USA, 2019. [Google Scholar]
- Clemente, C.; Pallotta, L.; De Maio, A.; Soraghan, J.J.; Farina, A. A novel algorithm for radar classification based on doppler characteristics exploiting orthogonal Pseudo-Zernike polynomials. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 417–430. [Google Scholar] [CrossRef] [Green Version]
- Du, L.; Li, L.; Wang, B.; Xiao, J. Micro-Doppler Feature Extraction Based on Time-Frequency Spectrogram for Ground Moving Targets Classification With Low-Resolution Radar. IEEE Sens. J. 2016, 16, 3756–3763. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, F. Radar imaging of micromotion targets from corrupted data. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2789–2802. [Google Scholar] [CrossRef]
- Addabbo, P.; Clemente, C.; Ullo, S.L. Fourier independent component analysis of radar micro-Doppler features. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017; pp. 45–49. [Google Scholar] [CrossRef] [Green Version]
- Persico, A.R.; Clemente, C.; Gaglione, D.; Ilioudis, C.V.; Cao, J.; Pallotta, L.; De Maio, A.; Proudler, I.; Soraghan, J.J. On Model, Algorithms, and Experiment for Micro-Doppler-Based Recognition of Ballistic Targets. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1088–1108. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, R.M.; Zenaldin, M. Radar micro-Doppler signatures of various human activities. IET Radar Sonar Navig. 2015, 9, 1205–1215. [Google Scholar] [CrossRef]
- Le, H.T.; Phung, S.L.; Bouzerdoum, A. Human Gait Recognition with Micro-Doppler Radar and Deep Autoencoder. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 3347–3352. [Google Scholar] [CrossRef]
- Garreau, G.; Andreou, C.M.; Andreou, A.G.; Georgiou, J.; Dura-Bernal, S.; Wennekers, T.; Denham, S. Gait-based person and gender recognition using micro-doppler signatures. In Proceedings of the 2011 IEEE Biomedical Circuits and Systems Conference (BioCAS), San Diego, CA, USA, 10–12 November 2011; pp. 444–447. [Google Scholar] [CrossRef]
- Cao, P.; Xia, W.; Ye, M.; Zhang, J.; Zhou, J. Radar-ID: Human identification based on radar micro-Doppler signatures using deep convolutional neural networks. IET Radar Sonar Navig. 2018, 12, 729–734. [Google Scholar] [CrossRef]
- Vandersmissen, B.; Knudde, N.; Jalalvand, A.; Couckuyt, I.; Bourdoux, A.; De Neve, W.; Dhaene, T. Indoor Person Identification Using a Low-Power FMCW Radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3941–3952. [Google Scholar] [CrossRef] [Green Version]
- Deng, L.; Yu, D. Deep learning: Methods and applications. Found. Trends Signal Process. 2014, 7, 197–387. [Google Scholar] [CrossRef] [Green Version]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Yang, Z.; Yang, D.; Dyer, C.; He, X.; Smola, A.; Hovy, E. Hierarchical Attention Networks for Document Classification. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; Association for Computational Linguistics: San Diego, CA, USA, 2016; pp. 1480–1489. [Google Scholar] [CrossRef] [Green Version]
- Addabbo, P.; Bernardi, M.L.; Biondi, F.; Cimitile, M.; Clemente, C.; Orlando, D. Gait Recognition using FMCW Radar and Temporal Convolutional Deep Neural Networks. In Proceedings of the 2020 IEEE 7th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 22–24 June 2020; pp. 171–175. [Google Scholar] [CrossRef]
- Tahmoush, D.; Silvious, J. Radar micro-doppler for long range front-view gait recognition. In Proceedings of the 2009 IEEE 3rd International Conference on Biometrics: Theory, Applications, and Systems, Washington, DC, USA, 28–30 September 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Z.; Andreou, A.G. Human identification experiments using acoustic micro-Doppler signatures. In Proceedings of the 2008 Argentine School of Micro-Nanoelectronics, Technology and Applications, Buenos Aires, Argentina, 18–19 September 2008; pp. 81–86. [Google Scholar]
- Reynolds, D. Gaussian Mixture Models. In Encyclopedia of Biometrics; Li, S.Z., Jain, A., Eds.; Springer US: Boston, MA, USA, 2009; pp. 659–663. [Google Scholar] [CrossRef]
- Giorgi, G.; Martinelli, F.; Saracino, A.; Alishahi, M.S. Walking Through the Deep: Gait Analysis for User Authentication through Deep Learning. In IFIP Advances in Information and Communication Technology, Proceedings of the SEC: IFIP International Conference on ICT Systems Security and Privacy Protection, Poznan, Poland, 18–20 September 2018; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Luo, F.; Poslad, S.; Bodanese, E. Human Activity Detection and Coarse Localization Outdoors Using Micro-Doppler Signatures. IEEE Sens. J. 2019, 19, 8079–8094. [Google Scholar] [CrossRef]
- Aloysius, N.; Geetha, M. A review on deep convolutional neural networks. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 6–8 April 2017; pp. 0588–0592. [Google Scholar] [CrossRef]
- Kim, Y.; Moon, T. Human Detection and Activity Classification Based on Micro-Doppler Signatures Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 8–12. [Google Scholar] [CrossRef]
- Shao, Y.; Dai, Y.; Yuan, L.; Chen, W. Deep Learning Methods for Personnel Recognition Based on Micro-Doppler Features. In Proceedings of the 9th International Conference on Signal Processing Systems, Auckland, New Zealand, 27–30 November 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 94–98. [Google Scholar] [CrossRef]
- Chen, V.; Ling, H. Time-Frequency Transforms for Radar Imaging and Signal Analysis; Artech: Morristown, NJ, USA, 2001. [Google Scholar]
- Chen, V.C. Analysis of radar micro-Doppler with time-frequency transform. In Proceedings of the Tenth IEEE Workshop on Statistical Signal and Array Processing (Cat. No.00TH8496), Pocono Manor, PA, USA, 16 August 2000; pp. 463–466. [Google Scholar] [CrossRef]
- Boulic, R.; Thalmann, N.; Thalmann, D.A. A global human walking model with real-time kinematic personification. Vis. Comput. 1990, 6, 344–358. [Google Scholar] [CrossRef]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. R. Stat. Soc. 1974, 36, 111–147. [Google Scholar] [CrossRef]
- Bernardi, M.; Cimitile, M.; Martinelli, F.; Mercaldo, F. Driver and path detection through time-series classification. J. Adv. Transp. 2018, 2018. [Google Scholar] [CrossRef]
- Ardimento, P.; Aversano, L.; Bernardi, M.L.; Cimitile, M. Temporal Convolutional Networks for Just-in-Time Software Defect Prediction. In Proceedings of the 15th International Conference on Software Technologies, ICSOFT 2020, Lieusaint, Paris, France, 7–9 July 2020; van Sinderen, M., Fill, H., Maciaszek, L.A., Eds.; ScitePress: Setúbal, Portugal, 2020; pp. 384–393. [Google Scholar] [CrossRef]
- Bernardi, M.L.; Cimitile, M.; Martinelli, F.; Mercaldo, F. Keystroke Analysis for User Identification using Deep Neural Networks. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Misra, D. Mish: A Self Regularized Non-Monotonic Neural Activation Function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 7–9 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- Mannor, S.; Peleg, D.; Rubinstein, R. The Cross Entropy Method for Classification. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 561–568. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the Importance of Initialization and Momentum in Deep Learning. In Proceedings of the 30th International Conference on International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; Volume 28, pp. III-1139–III-1147. [Google Scholar]
- Fioranelli, D.F.; Shah, D.S.A.; Li1, H.; Shrestha, A.; Yang, D.S.; Kernec, D.J.L. Radar sensing for healthcare. Electron. Lett. 2019, 55, 1022–1024. [Google Scholar] [CrossRef] [Green Version]
- Powers, D.M.W. Evaluation: From precision, recall and f-measure to roc., informedness, markedness & correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Schaul, T.; Antonoglou, I.; Silver, D. Unit Tests for Stochastic Optimization. arXiv 2013, arXiv:1312.6055. [Google Scholar]
- Wang, Y.; Liu, J.; Mišić, J.; Mišić, V.B.; Lv, S.; Chang, X. Assessing Optimizer Impact on DNN Model Sensitivity to Adversarial Examples. IEEE Access 2019, 7, 152766–152776. [Google Scholar] [CrossRef]
- Liu, S.; Deng, W. Very deep convolutional neural network based image classification using small training sample size. In Proceedings of the 2015 3rd IAPR Asian Conference on Pattern Recognition (ACPR), Kuala Lumpur, Malaysia, 3–6 November 2015; pp. 730–734. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]









| range from center of (x’,y’,z’) to radar in (x,y,z) | |
| range from point-target to radar in (x,y,z) | |
| range from point-target to center of (x’,y’,z’) | |
| vibration frequency | |
| azimuth angle of the center of (x’,y’,z’) | |
| elevation angle of center of (x’,y’,z’) | |
| azimuth angle of P relative to center of (x’,y’,z’) | |
| elevation angle of P relative to center of (x’,y’,z’) |
| Hyperparameters | Acronym | Optimized Ranges and Sets |
|---|---|---|
| Activation function | AF | {ReLU, Swish, Mish} |
| Batch size | BS | { 32, 64, 128, 256 } |
| Learning rate | LR | [0.09, 0.15] |
| Network size | NS | {Small, Medium, Large} |
| Number of layers | L | { 6, 7, 8, 9 } |
| Optimization algorithm | OA | {SGD, Nadam, RMSprop} |
| Window size | WS | {64, 128, 256} |
| Targets | AF | NS | LR | NL | BS | OA | WS | Precision | Recall | F1 | Accuracy | AUC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Swish | Medium | 0.12 | 6 | 64 | Nadam | 128 | 0.984 | 0.978 | 0.991 | 0.984 | 0.989 | |
| 10 | ReLu | Medium | 0.15 | 6 | 128 | SGD | 128 | 0.970 | 0.963 | 0.977 | 0.968 | 0.971 |
| ReLu | Small | 0.09 | 8 | 128 | SGD | 64 | 0.952 | 0.952 | 0.960 | 0.950 | 0.961 | |
| Mish | Large | 0.12 | 7 | 32 | Nadam | 128 | 0.852 | 0.901 | 0.922 | 0.911 | 0.916 | |
| 50 | Swish | Medium | 0.10 | 8 | 32 | SGD | 128 | 0.798 | 0.839 | 0.892 | 0.871 | 0.895 |
| Swish | Medium | 0.12 | 8 | 64 | SGD | 128 | 0.773 | 0.811 | 0.872 | 0,825 | 0.859 | |
| Mish | Large | 0.15 | 9 | 16 | Nadam | 128 | 0.849 | 0.898 | 0.885 | 0.891 | 0.890 | |
| 100 | Mish | Large | 0.14 | 9 | 32 | RMSProp | 128 | 0.830 | 0.851 | 0.838 | 0.862 | 0.871 |
| Mish | Large | 0.15 | 9 | 32 | SGD | 256 | 0.789 | 0.823 | 0.788 | 0.838 | 0.849 |
| Target | Network | Accuracy | Precision | Recall | F1 | AUC |
|---|---|---|---|---|---|---|
| VGG16 | 0,886 | 0.918 | 0.921 | 0.919 | 0.920 | |
| VGG19 | 0.932 | 0.948 | 0.983 | 0.965 | 0.969 | |
| 10 | RESNET | 0.969 | 0.960 | 0.982 | 0.971 | 0.973 |
| CNN2D | 0.879 | 0.856 | 0.926 | 0.890 | 0.890 | |
| TCN | 0.984 | 0.978 | 0.991 | 0.984 | 0.989 | |
| VGG16 | 0.832 | 0.897 | 0.843 | 0.869 | 0.872 | |
| VGG19 | 0.843 | 0.853 | 0.915 | 0.883 | 0.886 | |
| 50 | RESNET | 0.850 | 0.880 | 0.851 | 0.865 | 0.868 |
| CNN2D | 0.766 | 0.807 | 0.822 | 0.815 | 0.817 | |
| TCN | 0.852 | 0.901 | 0.922 | 0.911 | 0.916 | |
| VGG16 | 0.834 | 0.844 | 0.815 | 0.829 | 0.830 | |
| VGG19 | 0.838 | 0.852 | 0.883 | 0.867 | 0.870 | |
| 100 | RESNET | 0.831 | 0.832 | 0.821 | 0.827 | 0.831 |
| CNN2D | 0.812 | 0.784 | 0.847 | 0.814 | 0.816 | |
| TCN | 0.849 | 0.898 | 0.885 | 0.891 | 0.890 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Addabbo, P.; Bernardi, M.L.; Biondi, F.; Cimitile, M.; Clemente, C.; Orlando, D. Temporal Convolutional Neural Networks for Radar Micro-Doppler Based Gait Recognition. Sensors 2021, 21, 381. https://doi.org/10.3390/s21020381
Addabbo P, Bernardi ML, Biondi F, Cimitile M, Clemente C, Orlando D. Temporal Convolutional Neural Networks for Radar Micro-Doppler Based Gait Recognition. Sensors. 2021; 21(2):381. https://doi.org/10.3390/s21020381
Chicago/Turabian StyleAddabbo, Pia, Mario Luca Bernardi, Filippo Biondi, Marta Cimitile, Carmine Clemente, and Danilo Orlando. 2021. "Temporal Convolutional Neural Networks for Radar Micro-Doppler Based Gait Recognition" Sensors 21, no. 2: 381. https://doi.org/10.3390/s21020381
APA StyleAddabbo, P., Bernardi, M. L., Biondi, F., Cimitile, M., Clemente, C., & Orlando, D. (2021). Temporal Convolutional Neural Networks for Radar Micro-Doppler Based Gait Recognition. Sensors, 21(2), 381. https://doi.org/10.3390/s21020381