Life Prediction of Battery Using a Neural Gaussian Process with Early Discharge Characteristics
Abstract
:1. Introduction
2. Battery Data Preparation
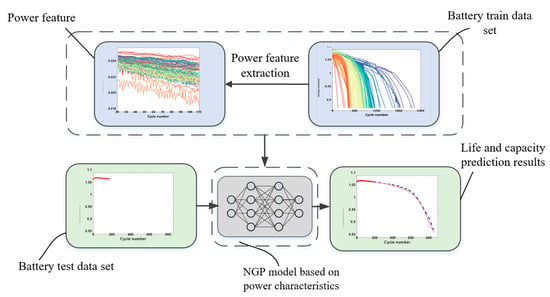
3. Physical Feature Extraction
4. Methodology
4.1. Neural Gaussian Process Model
4.2. Prediction Framework
5. Results and Description
5.1. Cycle Life Prediction
5.2. Capacity Prediction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jang, B.; Koo, J.; Park, M.; Lee, H.; Nam, J.; Kwon, Y.; Lee, H. Graphdiyne as a high-capacity lithium ion battery anode material. Appl. Phys. Lett. 2013, 103, 263904-1–263904-5. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Alshareef, H.N.; Schwingenschlögl, U. Functionalized NbS2 as cathode for Li- and Na-ion batteries. Appl. Phys. Lett. 2017, 111, 043903-1–043903-5. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Lai, X.; Hu, X. Micro-Short-Circuit Diagnosis for Series-Connected Lithium-Ion Battery Packs Using Mean-Difference Model. IEEE Trans. Ind. Electron. 2019, 66, 2132–2142. [Google Scholar] [CrossRef]
- Gu, M.; Shi, W.; Zheng, J.; Yan, P.; Zhang, J.; Wang, C. Probing the failure mechanism of nanoscale LiFePO4 for Li-ion batteries. Appl. Phys. Lett. 2015, 106, 203902-1–203902-3. [Google Scholar] [CrossRef]
- Zhang, Q.; Han, L.; Pan, J.; Chen, Z.; Cheng, Y. Chemically stable artificial SEI for Li-ion battery electrodes. Appl. Phys. Lett. 2017, 110, 133901-1–133901-5. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Chen, Z.Q. Remaining useful life prediction of lithium-ion batteries based on health indicator and Gaussian process regression model. IEEE Access. 2019, 7, 39474–39484. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, Y.; Lu, S.; Wang, J.; Zhang, X. Remaining Useful Life Prediction of Lithium-Ion Batteries Using Support Vector Regression Optimized by Artificial Bee Colony. IEEE Trans. Veh. Technol. 2019, 68, 9543–9553. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Mierlo, J.V.; Bossche, P.V.D. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, Y.; Zhou, X.; Chen, H. Remaining Useful Life Prediction of Lithium-Ion Battery Based on Gauss–Hermite Particle Filter. IEEE Trans. Control Syst. Technol. 2019, 27, 1788–1795. [Google Scholar] [CrossRef]
- Wang, H.; Song, W.; Zio, E.; Kudreyko, A.; Zhang, Y. Remaining useful life prediction for Lithium-ion batteries using fractional Brownian motion and Fruit-fly Optimization Algorithm. Measurement 2020, 161, 107904-1–107904-9. [Google Scholar] [CrossRef]
- Shuvo, M.A.I.; Rodriguez, G.; Islam, M.T.; Karim, H.; Ramabadran, N.; Noveron, J.C.; Lin, Y. Microwave exfoliated graphene oxide/TiO2 nanowire hybrid for high performance lithium ion battery. J. Appl. Phys. 2015, 118, 125102-1–125102-5. [Google Scholar] [CrossRef] [Green Version]
- Kawasaki, M.; Laokawee, V.; Sarakonsri, T.; Hashizume, T.; Shiojiri, M. Structural investigation of SiSn/(reduced graphene oxide) nanocomposite powder for Li-ion battery anode applications. J. Appl. Phys. 2016, 120, 204302-1–204302-6. [Google Scholar] [CrossRef]
- Chen, L.; Lü, Z.; Lin, W.; Li, J.; Pan, H. A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity. Measurement 2018, 116, 586–595. [Google Scholar] [CrossRef]
- Salkind, A.J.; Fennie, C.; Singh, P.; Atwater, T.; Reisner, D.E. Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology. J. Power Sources 1999, 80, 293–300. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Woirgard, E.; Vinassa, J.M. Remaining useful life prediction of lithium batteries in calendar ageing for automotive applications. Microelectron. Reliab. 2012, 52, 2438–2442. [Google Scholar] [CrossRef]
- Pattipati, B.; Sankavaram, C.; Pattipati, K. System identification and estimation framework for pivotal automotive battery management system characteristics. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2011, 41, 869–884. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.; Tsui, K.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Zheng, X.; Fang, H. An integrated unscented Kalman filter and relevance vector regression approach for lithium-ion battery remaining useful life and short-term capacity prediction. Reliab. Eng. Syst. Saf. 2015, 144, 74–82. [Google Scholar] [CrossRef]
- Su, X.; Wang, S.; Pecht, M.; Zhao, L.; Ye, Z. Interacting multiple model particle filter for prognostics of lithium-ion batteries. Microelectron. Reliab. 2017, 70, 59–69. [Google Scholar] [CrossRef]
- Sahinoglu, G.O.; Pajovic, M.; Sahinoglu, Z.; Wang, Y.B.; Orlik, P.V.; Wada, T. Battery state-of-charge estimation based on regular/recurrent Gaussian process regression. IEEE Trans. Ind. Electron. 2018, 65, 4311–4321. [Google Scholar] [CrossRef]
- Ng, S.; Xing, Y.; Tsui, K. A naive Bayes model for robust remaining useful life prediction of lithium-ion battery. Appl. Energy 2014, 118, 114–123. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Sources 2013, 239, 253–264. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, J.; Liao, H.; Peng, Y.; Peng, X. A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 915–928. [Google Scholar]
- Zhou, Y.; Huang, M.; Chen, Y.; Tao, Y. A novel health indicator for on-line lithium-ion batteries remaining useful life prediction. J. Power Sources 2016, 321, 1–10. [Google Scholar] [CrossRef]
- Widodo, A.; Shim, M.; Caesarendra, W.; Yang, B. Intelligent prognostics for battery health monitoring based on sample entropy. Expert Syst. Appl. 2011, 38, 11763–11769. [Google Scholar] [CrossRef]
- Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Doo, S. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Peng, Y.; Hou, Y.; Song, Y.; Pang, J.; Liu, D. Lithium-Ion Battery Prognostics with Hybrid Gaussian Process Function Regression. Energies 2018, 11, 1420. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Zhang, C.; Chen, Z. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks. Appl. Energy 2016, 173, 134–140. [Google Scholar] [CrossRef]
- Khumprom, P.; Yodo, N. A Data-Driven Predictive Prognostic Model for Lithium-ion Batteries based on a Deep Learning Algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef] [Green Version]
- Chang, W. Estimation of the state of charge for a LFP battery using a hybrid method that combines a RBF neural network, an OLS algorithm and AGA. Int. J. Electr. Power Energy Syst. 2013, 53, 603–611. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Garnelo, M.; Schwarz, J.; Rosenbaum, D.; Viola, F.; Rezende, D.J.; Eslami, S.M.; Teh, Y.W. Neural Processes. arXiv Prepr. 2018, arXiv:1807.01622. [Google Scholar]
- Kim, H.; Mnih, A.; Schwarz, J.; Garnelo, M.; Eslami, A.; Rosenbaum, D.; Vinyals, O.; Teh, Y.W. Attentive Neural Processes. arXiv Prepr. 2019, arXiv:1901.05761. [Google Scholar]
- Seeger, M. Gaussian Processes for Machine Learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]










| Data Set | MAPE of Model with Characteristics | |||
|---|---|---|---|---|
| Power with NGP (%) | Power with RBFNN (%) | Voltage with NGP (%) | Voltage with RBFNN (%) | |
| Train | 8.4 | 10.2 | 9.3 | 10.5 |
| First test | 12.0 (8.8) | 13.8 (10.1) | 12.7 (10.7) | 14.7 (12.5) |
| Second test | 8.8 | 9.8 | 11.9 | 12.6 |
| Model | Cycle Life 335 | Cycle Life 854 | Cycle Life 1028 | Cycle Life 1638 |
|---|---|---|---|---|
| Power P predicted cycle life | 353 | 856 | 1037 | 1638 |
| NGP predicted failure cycle (110 cycles) | 339 | 834 | 1006 | 1581 |
| NGP predicted failure cycle (20% predicted of cycle life) | 342 | 840 | 1020 | 1588 |
| RBFNN predicted failure cycle (110 cycles) | 315 | 731 | 861 | 1828 |
| RBFNN predicted failure cycle (20% predicted of cycle life) | 291 | 830 | 1043 | 1712 |
| Model | Cycle Life 335 (%) | Cycle Life 854 (%) | Cycle Life 1028 (%) | Cycle Life 1638 (%) |
|---|---|---|---|---|
| NGP with 110 cycles | 1.2 | 2.3 | 2.1 | 3.5 |
| NGP with 20% predicted of cycle life | 2.1 | 1.6 | 0.8 | 3.1 |
| RBFNN with 110 cycles | 6.0 | 14.4 | 16.2 | 11.6 |
| RBFNN with 20% predicted of cycle life | 13.1 | 2.8 | 1.4 | 4.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, A.; Tan, Z.; Tan, J. Life Prediction of Battery Using a Neural Gaussian Process with Early Discharge Characteristics. Sensors 2021, 21, 1087. https://doi.org/10.3390/s21041087
Yin A, Tan Z, Tan J. Life Prediction of Battery Using a Neural Gaussian Process with Early Discharge Characteristics. Sensors. 2021; 21(4):1087. https://doi.org/10.3390/s21041087
Chicago/Turabian StyleYin, Aijun, Zhibin Tan, and Jian Tan. 2021. "Life Prediction of Battery Using a Neural Gaussian Process with Early Discharge Characteristics" Sensors 21, no. 4: 1087. https://doi.org/10.3390/s21041087
APA StyleYin, A., Tan, Z., & Tan, J. (2021). Life Prediction of Battery Using a Neural Gaussian Process with Early Discharge Characteristics. Sensors, 21(4), 1087. https://doi.org/10.3390/s21041087