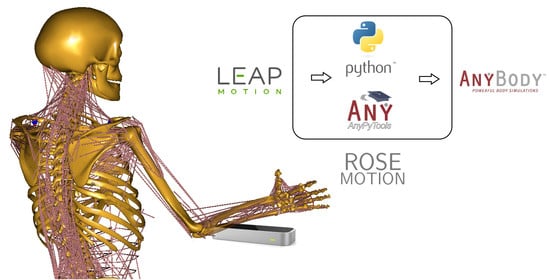
Hand Motion Capture from a 3D Leap Motion Controller for a Musculoskeletal Dynamic Simulation
Abstract
:1. Introduction
2. Methods
2.1. General Approach
- Marker-based C3D (three-dimensional time-sequence data) and Biovision Hierarchy (BVH) files for MoCap simulation:Imported trajectories of marker coordinates are fitted to model attached points using the AnyMoCap™ Framework [21]. An optimization algorithm calculates the motion of the arm while maintaining the minimum distance to the linked markers (Figure 1a) possible. This procedure requires manual adaptions of the initial position, marker alignment, and mapping prior to the simulation.
- Joint angle interpolation:For each joint (i.e., wrist) and each degree of freedom (flexion/extension, abduction/adduction, and pronation/supination) a (time)series of recorded angles is interpolated with a B-spline and the resulting continuous function is used to drive the respective joint. For that, the recorded motion has to be converted into subsequent joint angles and transferred into the AMS study. A neutral-zero position of the arm is used as a reference position to which all following positions are compared. The calculated joint angles will therefore describe the motion to drive the joints from the initial position to the recorded position (Figure 1b).
2.2. Workflow
2.2.1. Recording with the LMC
2.2.2. Calculate Joint Angles
- rotation about the flexion and extension axis (X-axis, ),
- rotation about the resultant abduction and adduction axis (Y-axis, ), and
- rotation about the resultant rotation axis (Z-axis, ).
2.2.3. Transfer Motion Data to the AMS
2.2.4. AMS Analysis
2.3. Validation
3. Results
3.1. Motion Recording and Simulation with ROSE Motion
- RecordIn the Record function, various settings can be made. It can be specified with how many frames per second the recording is executed. Furthermore, it can be decided whether interpolation files and/or a BVH file is written and its storage location. While recording, a window opens in which the tracked hand movement is visualized in real-time. Upon completion of the recording, an animation to view every frame of the recorded hand is shown.
- AnyBodyThe AMS simulation can be started in the AnyBody feature. Different file sources (including BVH) can be selected, which are modified and copied to the correct location. In addition, one can specify which frames should be included in the simulation (start frame and end frame). Then, all studies to be run by the AMS (initial conditions, kinematic analysis, and inverse-dynamic analysis) can be selected (see Section 2.2.4). Once the simulation has finished, the AMS will be opened and shows a replay of the calculated movement. Further analyses inside the AMS are then directly possible.
- ConverterIn the Convert component, a given BVH file can be converted to the interpolation files used for the AMS.
- AnimationOpens a BVH file to animate it, a slider can be used to iterate through the frames.
3.2. Accuracy Measurement
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMS | AnyBody™ Modeling System |
| BVH | Biovision Hierarchy |
| C3D | Three-Dimensional Time-Sequence Data |
| DP | Distal Phalanges |
| IP | Intermediate Phalanges |
| LMC | Leap Motion Controller |
| MC | Metacarpals |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MoCap | Motion Capture |
| PP | Proximal Phalanges |
| UVC | Universal Video Class |
References
- Engelhardt, L.; Melzner, M.; Havelkova, L.; Christen, P.; Dendorfer, S.; Simon, U. A new musculoskeletal AnyBody™ detailed hand model. J. Comput. Methods Biomech. Biomed. Eng. 2020. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, J.; Damsgaard, M.; Surma, E.; Christensen, S.T.; de Zee, M.; Vondrak, V. AnyBody-a software system for ergonomic optimization. In Proceedings of the Fifth World Congress on Structural and Multidisciplinary Optimization 2003, Milano, Italy, 19–23 May 2003; pp. 231–232. [Google Scholar]
- Skals, S.; Rasmussen, K.P.; Bendtsen, K.M.; Yang, J.; Andersen, M.S. A musculoskeletal model driven by dual Microsoft Kinect Sensor data. Multibody Syst. Dyn. 2017, 41, 297–316. [Google Scholar] [CrossRef] [Green Version]
- Gragg, J.; Yang, J.J.; Boothby, R. Posture Reconstruction Method for Mapping Joint Angles of Motion Capture Experiments to Simulation Models. In Proceedings of the International Conference on Digital Human Modeling 2011, Orlando, FL, USA, 9–14 July 2011; pp. 69–78. [Google Scholar] [CrossRef]
- Khademi, M.; Mousavi Hondori, H.; McKenzie, A.; Dodakian, L.; Lopes, C.V.; Cramer, S.C. Free-hand interaction with leap motion controller for stroke rehabilitation. In Proceedings of the Extended Abstracts of the 32nd Annual ACM Conference on Human Factors in Computing Systems, Toronto, ON, Canada, 26 April–1 May 2014; pp. 1663–1668. [Google Scholar] [CrossRef] [Green Version]
- Iosa, M.; Morone, G.; Fusco, A.; Castagnoli, M.; Fusco, F.R.; Pratesi, L.; Paolucci, S. Leap motion controlled videogame-based therapy for rehabilitation of elderly patients with subacute stroke: A feasibility pilot study. Top. Stroke Rehabil. 2015, 22, 306–316. [Google Scholar] [CrossRef] [PubMed]
- Holmes, D.E.; Charles, D.K.; Morrow, P.J.; McClean, S.; McDonough, S. Using Fitt’s Law to Model Arm Motion Tracked in 3D by a Leap Motion Controller for Virtual Reality Upper Arm Stroke Rehabilitation. In Proceedings of the 2016 IEEE 29th International Symposium on Computer-Based Medical Systems (CBMS), Dublin, Ireland, 20–24 June 2016; pp. 335–336. [Google Scholar] [CrossRef]
- Weichert, F.; Bachmann, D.; Rudak, B.; Fisseler, D. Analysis of the Accuracy and Robustness of the Leap Motion Controller. Sensors 2013, 13, 6380–6393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guna, J.; Jakus, G.; Pogačnik, M.; Tomažič, S.; Sodnik, J. An Analysis of the Precision and Reliability of the Leap Motion Sensor and Its Suitability for Static and Dynamic Tracking. Sensors 2014, 14, 3702–3720. [Google Scholar] [CrossRef] [Green Version]
- Niechwiej-Szwedo, E.; Gonzalez, D.; Nouredanesh, M.; Tung, J. Evaluation of the Leap Motion Controller during the performance of visually-guided upper limb movements. PLoS ONE 2018, 13, e0193639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chophuk, P.; Chumpen, S.; Tungjitkusolmun, S.; Phasukkit, P. Hand postures for evaluating trigger finger using leap motion controller. In Proceedings of the 2015 8th Biomedical Engineering International Conference (BMEiCON), Pattaya, Thailand, 25–27 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Smeragliuolo, A.H.; Hill, N.J.; Disla, L.; Putrino, D. Validation of the Leap Motion Controller using markered motion capture technology. J. Biomech. 2016, 49, 1742–1750. [Google Scholar] [CrossRef] [PubMed]
- Nizamis, K.; Rijken, N.; Mendes, A.; Janssen, M.; Bergsma, A.; Koopman, B. A Novel Setup and Protocol to Measure the Range of Motion of the Wrist and the Hand. Sensors 2018, 18, 3230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rühlicke, M. Fusion der Daten Zweier Leap Motion Sensoren. Master’s Thesis, Technische Universität Dresden, Dresden, Germany, 2017. [Google Scholar]
- Python Software Foundation. Python. Version 3.7.2. 2019. Available online: https://www.python.org/downloads/release/python-372 (accessed on 4 September 2019).
- Kiehl, C. Gooey. Version 12 March 2019. 2019. Available online: https://github.com/chriskiehl/Gooey (accessed on 6 December 2019).
- Lund, M.; Rasmussen, J.; Andersen, M. AnyPyTools: A Python package for reproducible research with the AnyBody Modeling System. J. Open Source Softw. 2019, 4, 1108. [Google Scholar] [CrossRef]
- Leap Motion. LeapCxx. Version 8 August 2018. 2018. Available online: https://github.com/leapmotion/LeapCxx (accessed on 16 October 2019).
- Alemi, O. PyMO. Version 19 November 2017. 2017. Available online: https://github.com/omimo/PyMO (accessed on 20 September 2019).
- Fonk, R.; Schneeweiss, S. ROSE Motion. Version 1.0.0. 2020. Available online: https://github.com/seanschneeweiss/RoSeMotion (accessed on 10 April 2020).
- Lund, M.E.; Tørholm, S.; Jung, M. The AnyBody Managed Model Repository (AMMR) (Version 2.1.1). Zenodo 2018. [Google Scholar] [CrossRef]
- PubNub Staff. Motion-controlled Servos with Leap Motion & Raspberry Pi. Available online: https://www.pubnub.com/blog/2015-08-19-motion-controlled-servos-with-leap-motion-raspberry-pi (accessed on 19 August 2015).
- Schmidt, R.; Disselhorst-Klug, C.; Silny, J.; Rau, G. A marker-based measurement procedure for unconstrained wrist and elbow motions. J. Biomech. 1999, 32, 615–621. [Google Scholar] [CrossRef]
- Disselhorst-Klug, C.; Besdo, S.; Oehler, S. Biomechanik des muskuloskelettalen Systems. Biomed. Tech. Rehabil. 2015, 10, 53–105. [Google Scholar] [CrossRef]
- Williams, S.; Schmidt, R.; Disselhorst-Klug, C.; Rau, G. An upper body model for the kinematical analysis of the joint chain of the human arm. J. Biomech. 2006, 39, 2419–2429. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, H.; Poole, C.P.; Safko, J.L. (Eds.) Klassische Mechanik, 3rd ed.; Lehrbuch Physik, Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar]
- Barton, C. Blender-Mathutils. Version 26 September 2018. 2018. Available online: https://gitlab.com/ideasman42/blender-mathutils (accessed on 20 September 2019).
- Leap Motion. Logo. Available online: https://www.leapmotion.com/press/ (accessed on 21 May 2019).
- Danish Yellowpages. AnyBody Technology. Available online: https://www.yellowpages.dk/c/anybody-technology-a-s (accessed on 21 May 2019).
- Lund, M.E. AnyPyTools’ Documentation! Version 1.1.2. 2019. Available online: https://anybody-research-group.github.io/anypytools-docs (accessed on 27 September 2019).
- Brown, D.; Hanson, R.; Christian, W. Tracker Video Analysis and Modeling Tool. Version 4.11.0. 2018. Available online: https://physlets.org/tracker/index.html (accessed on 12 March 2020).
- Flaticon. Best Icons. Available online: https://www.flaticon.com/ (accessed on 21 May 2019).
- WorldVectorLogo. Python Vector Logo. Available online: https://worldvectorlogo.com/logo/python-4 (accessed on 21 May 2019).
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; et al. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef] [PubMed]
- Leap Motion. Version 8 December 2018. Introducing LeapUVC: A New API for Education, Robotics and More. 2018. Available online: http://blog.leapmotion.com/leapuvc/ (accessed on 11 September 2019).
- Placidi, G.; Cinque, L.; Polsinelli, M.; Spezialetti, M. Measurements by A LEAP-Based Virtual Glove for the Hand Rehabilitation. Sensors 2018, 18, 834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leap Motion. Version 20 December 2018. Experimental Release 2: Multiple Device Support. 2018. Available online: http://blog.leapmotion.com/multiple-devices/ (accessed on 6 February 2020).











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fonk, R.; Schneeweiss, S.; Simon, U.; Engelhardt, L. Hand Motion Capture from a 3D Leap Motion Controller for a Musculoskeletal Dynamic Simulation. Sensors 2021, 21, 1199. https://doi.org/10.3390/s21041199
Fonk R, Schneeweiss S, Simon U, Engelhardt L. Hand Motion Capture from a 3D Leap Motion Controller for a Musculoskeletal Dynamic Simulation. Sensors. 2021; 21(4):1199. https://doi.org/10.3390/s21041199
Chicago/Turabian StyleFonk, Robin, Sean Schneeweiss, Ulrich Simon, and Lucas Engelhardt. 2021. "Hand Motion Capture from a 3D Leap Motion Controller for a Musculoskeletal Dynamic Simulation" Sensors 21, no. 4: 1199. https://doi.org/10.3390/s21041199
APA StyleFonk, R., Schneeweiss, S., Simon, U., & Engelhardt, L. (2021). Hand Motion Capture from a 3D Leap Motion Controller for a Musculoskeletal Dynamic Simulation. Sensors, 21(4), 1199. https://doi.org/10.3390/s21041199