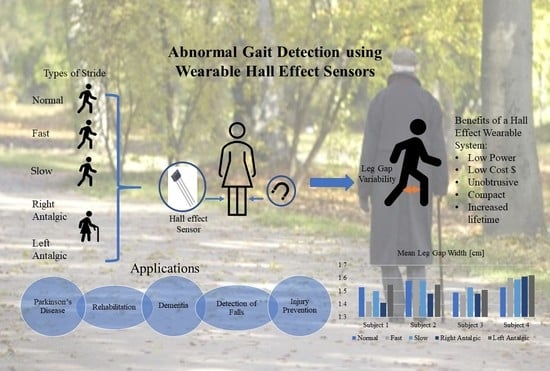
Abnormal Gait Detection Using Wearable Hall-Effect Sensors
Abstract
:1. Introduction
1.1. Gait Parameters
1.2. Gait Monitoring and Analysis
1.3. Gait Monitoring Technologies
1.4. This Study
2. Materials and Methods
- RQ1: Does leg gap width captured using the wearable system make a sufficient proxy for stride width in terms of differentiating abnormal and irregular strides from normal strides?
- RQ2: Can the wearable system capture cadence with sufficient accuracy to differentiate abnormal and irregular strides from normal strides?
3. Results
Leg Gap Width (as a Proxy for Stride Width)
4. Discussion
4.1. Research Question 1 (RQ1)
Does leg gap width captured using the wearable system make a sufficient proxy for stride width in terms of differentiating abnormal and irregular strides from normal?
4.2. Research Question 2 (RQ2)
Can the wearable system capture cadence with sufficient accuracy to differentiate abnormal and irregular strides from normal strides?
4.3. Benchmarking—Comparison to Existing Wearables
4.4. Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moon, Y.; Sung, J.; An, R.; Hernandez, M.E.; Sosnoff, J.J. Gait Variability in People with Neurological Disorders: A Systematic Review and Meta-Analysis. Hum. Mov. Sci. 2016, 47, 197–208. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Rios, D.A.; Edelberg, H.K. Gait Variability and Fall Risk in Community-Living Older Adults: A 1-Year Prospective Study. Arch. Phys. Med. Rehabil. 2001, 82, 1050–1056. [Google Scholar] [CrossRef] [PubMed]
- Brach, J.S.; Studenski, S.; Perera, S.; VanSwearingen, J.M.; Newman, A.B. Stance Time and Step Width Variability Have Unique Contributing Impairments in Older Persons. Gait Posture 2008, 27, 431–439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lord, S.; Baker, K.; Nieuwboer, A.; Burn, D.; Rochester, L. Gait Variability in Parkinson’s Disease: An Indicator of Non-Dopaminergic Contributors to Gait Dysfunction? J. Neurol. 2011, 258, 566–572. [Google Scholar] [CrossRef] [PubMed]
- Hausdorff, J.M.; Cudkowicz, M.E.; Firtion, R.; Wei, J.Y.; Goldberger, A.L. Gait Variability and Basal Ganglia Disorders: Stride-to-Stride Variations of Gait Cycle Timing in Parkinson’s Disease and Huntington’s Disease. Mov. Disord. 1998, 13, 428–437. [Google Scholar] [CrossRef]
- Mileti, I.; Taborri, J.; Rossi, S.; Petrarca, M.; Patane, F.; Cappa, P. Evaluation of the Effects on Stride-to-Stride Variability and Gait Asymmetry in Children with Cerebral Palsy Wearing the WAKE-up Ankle Module. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Benevento, Italy, 15–18 May 2016; pp. 1–6. [Google Scholar]
- Chakravarthy, Y.K. Design and Development of an Indigenous and Intelligent Transfemoral Prosthetic Leg. Ph.D. Thesis, Koneru Lakshmaiah Education Foundation, Andhra Pradesh, India, 2018. [Google Scholar]
- Galna, B.; Lord, S.; Rochester, L. Is Gait Variability Reliable in Older Adults and Parkinson’s Disease? Towards an Optimal Testing Protocol. Gait Posture 2013, 37, 580–585. [Google Scholar] [CrossRef]
- Brach, J.S.; Berlin, J.E.; VanSwearingen, J.M.; Newman, A.B.; Studenski, S.A. Too Much or Too Little Step Width Variability Is Associated with a Fall History in Older Persons Who Walk at or near Normal Gait Speed. J. Neuroeng. Rehabil. 2005, 2, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Aboutorabi, A.; Arazpour, M.; Bahramizadeh, M.; Hutchins, S.W.; Fadayevatan, R. The Effect of Aging on Gait Parameters in Able-Bodied Older Subjects: A Literature Review. Aging Clin. Exp. Res. 2016, 28, 393–405. [Google Scholar] [CrossRef]
- Esser, P.; Dawes, H.; Collett, J.; Howells, K. Insights into Gait Disorders: Walking Variability Using Phase Plot Analysis, Parkinson’s Disease. Gait Posture 2013, 38, 648–652. [Google Scholar] [CrossRef] [PubMed]
- Lemke, M.R.; Wendorff, T.; Mieth, B.; Buhl, K.; Linnemann, M. Spatiotemporal Gait Patterns during over Ground Locomotion in Major Depression Compared with Healthy Controls. J. Psychiatr. Res. 2000, 34, 277–283. [Google Scholar] [CrossRef]
- Yong, J.R.; Silder, A.; Montgomery, K.L.; Fredericson, M.; Delp, S.L. Acute Changes in Foot Strike Pattern and Cadence Affect Running Parameters Associated with Tibial Stress Fractures. J. Biomech. 2018, 76, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Jankovic, J. Parkinson’s Disease: Clinical Features and Diagnosis. J. Neurol. Neurosurg. Psychiatry 2008, 79, 368–376. [Google Scholar] [CrossRef] [Green Version]
- Tao, W.; Liu, T.; Zheng, R.; Feng, H. Gait Analysis Using Wearable Sensors. Sensors 2012, 12, 2255–2283. [Google Scholar] [CrossRef]
- Bonato, P.; De Rossi, D.; Dittmar, A.; Jayaraman, S.; Korhonen, I.; Lymberis, A.; Adams, E.M.; Zhang, Y.-T. IEEE EMBS Technical Committee on Wearable Biomedical Sensors & Systems: Position Paper. In Proceedings of the International Workshop on Wearable and Implantable Body Sensor Networks (BSN’06), Cambridge, MA, USA, 3–5 April 2006; pp. 212–214. [Google Scholar]
- Rodgers, M.M.; Pai, V.M.; Conroy, R.S. Recent Advances in Wearable Sensors for Health Monitoring. IEEE Sens. J. 2015, 15, 3119–3126. [Google Scholar] [CrossRef]
- Majumder, S.; Mondal, T.; Deen, M. Wearable Sensors for Remote Health Monitoring. Sensors 2017, 17, 130. [Google Scholar] [CrossRef]
- Bamberg, S.; Benbasat, A.Y.; Scarborough, D.M.; Krebs, D.E.; Paradiso, J.A. Gait Analysis Using a Shoe-Integrated Wireless Sensor System. IEEE Trans. Inf. Technol. Biomed. 2008, 12, 413–423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jo, A.; Coronel, B.D.; Coakes, C.E.; Mainous, A.G. Is There a Benefit to Patients Using Wearable Devices Such as Fitbit or Health Apps on Mobiles? A Systematic Review. Am. J. Med. 2019, 132, 1394–1400.e1. [Google Scholar] [CrossRef]
- Harnessing Wearable Device Data to Improve State-Level Real-Time Surveillance of Influenza-like Illness in the USA: A Population-Based Study—The Lancet Digital Health. Available online: https://www.thelancet.com/journals/landig/article/PIIS2589-7500(19)30222-5/fulltext (accessed on 30 December 2020).
- Brown, D. “It Saved My Life”: Apple Watch, Fitbit Are Notifying Users of Medical Emergencies. Available online: https://www.usatoday.com/story/tech/2019/02/20/can-smartwatches-literally-save-lives-some-users-say-yes/2646598002/ (accessed on 30 December 2020).
- Oldham, A.; Stepien, K.M.; Hendriksz, C.J. Potential Benefits of Fitbit Device in Managing a Patient with Mucopolysaccharidosis. Mol. Genet. Metab. 2019, 126, S111. [Google Scholar] [CrossRef]
- Abrantes, A.M.; Blevins, C.E.; Battle, C.L.; Read, J.P.; Gordon, A.L.; Stein, M.D. Developing a Fitbit-Supported Lifestyle Physical Activity Intervention for Depressed Alcohol Dependent Women. J. Subst. Abuse Treat. 2017, 80, 88–97. [Google Scholar] [CrossRef]
- IDC—Wearable Devices Market Share. Available online: https://www.idc.com/promo/wearablevendor (accessed on 30 December 2020).
- Wu, X.; Chen, X.; Duan, Y.; Xu, S.; Cheng, N.; An, N. A Study on Gait-Based Parkinson’s Disease Detection Using a Force Sensitive Platform. In Proceedings of the 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Kansas City, MO, USA, 13–16 November 2017; pp. 2330–2332. [Google Scholar]
- Muro-de-la-Herran, A.; Garcia-Zapirain, B.; Mendez-Zorrilla, A. Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kobsar, D.; Masood, Z.; Khan, H.; Khalil, N.; Kiwan, M.Y.; Ridd, S.; Tobis, M. Wearable Inertial Sensors for Gait Analysis in Adults with Osteoarthritis—A Scoping Review. Sensors 2020, 20, 7143. [Google Scholar] [CrossRef]
- Hao, M.; Chen, K.; Fu, C. Smoother-Based 3-D Foot Trajectory Estimation Using Inertial Sensors. IEEE Trans. Biomed. Eng. 2019, 66, 3534–3542. [Google Scholar] [CrossRef]
- Yu, T.-H.; Wu, C.-C. An Accelerometer Based Gait Analysis System to Detect Gait Abnormalities in Cerebralspinal Meningitis Patients. In Proceedings of the 2019 International Conference on Machine Learning and Cybernetics (ICMLC), Kobe, Japan, 7–10 July 2019; pp. 1–5. [Google Scholar]
- Li, G.; Liu, T.; Yi, J. Wearable Sensor System for Detecting Gait Parameters of Abnormal Gaits: A Feasibility Study. IEEE Sens. J. 2018, 18, 4234–4241. [Google Scholar] [CrossRef]
- Hsi, W.-L.; Chai, H.-M.; Lai, J.-S. Comparison of Pressure and Time Parameters in Evaluating Diabetic Footwear. Am. J. Phys. Med. Rehabil. 2002, 81, 822–829. [Google Scholar] [CrossRef]
- Bai, O.; Atri, R.; Marquez, J.S.; Fei, D.-Y. Characterization of Lower Limb Activity during Gait Using Wearable, Multi-Channel Surface EMG and IMU Sensors. In Proceedings of the 2017 International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 8–10 March 2017; p. 4. [Google Scholar]
- Munoz-Organero, M.; Parker, J.; Powell, L.; Davies, R.; Mawson, S. Sensor Optimization in Smart Insoles for Post-Stroke Gait Asymmetries Using Total Variation and L 1 Distances. IEEE Sens. J. 2017, 17, 3142–3151. [Google Scholar] [CrossRef]
- Duong, P.; Suh, Y. Foot Pose Estimation Using an Inertial Sensor Unit and Two Distance Sensors. Sensors 2015, 15, 15888–15902. [Google Scholar] [CrossRef]
- López-Nava, I.H.; Muñoz-Meléndez, A.; Sanpablo, A.I.P.; Montero, A.A.; Urióstegui, I.Q.; Carrera, L.N. Estimation of Temporal Gait Parameters Using Bayesian Models on Acceleration Signals. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 396–403. [Google Scholar] [CrossRef]
- Makino, K.; Nakamura, M.; Omori, H.; Terada, H. Gait Analysis Using Gravity-Center Fluctuation of the Sole at Walking Based on Self-Organizing Map. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Rio de Janeiro, Brazil, 3–5 June 2015; pp. 900–905. [Google Scholar]
- Weenk, D.; Roetenberg, D.; van Beijnum, B.J.F.; Hermens, H.J.; Veltink, P.H. Ambulatory Estimation of Relative Foot Positions by Fusing Ultrasound and Inertial Sensor Data. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 817–826. [Google Scholar] [CrossRef]
- Djuric-Jovicic, M.D.; Jovicic, N.S.; Radovanovic, S.M.; Stankovic, I.D.; Popovic, M.B.; Kostic, V.S. Automatic Identification and Classification of Freezing of Gait Episodes in Parkinson’s Disease Patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 685–694. [Google Scholar] [CrossRef] [PubMed]
- Novak, D.; Goršič, M.; Podobnik, J.; Munih, M. Toward Real-Time Automated Detection of Turns during Gait Using Wearable Inertial Measurement Units. Sensors 2014, 14, 18800–18822. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taborri, J.; Rossi, S.; Palermo, E.; Patanè, F.; Cappa, P. A Novel HMM Distributed Classifier for the Detection of Gait Phases by Means of a Wearable Inertial Sensor Network. Sensors 2014, 14, 16212–16234. [Google Scholar] [CrossRef]
- Hung, T.N.; Suh, Y.S. Inertial Sensor-Based Two Feet Motion Tracking for Gait Analysis. Sensors 2013, 13, 5614–5629. [Google Scholar] [CrossRef] [PubMed]
- Salarian, A.; Burkhard, P.R.; Vingerhoets, F.J.G.; Jolles, B.M.; Aminian, K. A Novel Approach to Reducing Number of Sensing Units for Wearable Gait Analysis Systems. IEEE Trans. Biomed. Eng. 2013, 60, 72–77. [Google Scholar] [CrossRef]
- Sayeed, T.; Sama, A.; Catala, A.; Cabestany, J. Comparative and Adaptation of Step Detection and Step Length Estimators to a Lateral Belt Worn Accelerometer. In Proceedings of the 2013 IEEE 15th International Conference on e-Health Networking, Applications and Services (Healthcom 2013), Lisbon, Portugal, 9–12 October 2013; pp. 105–109. [Google Scholar]
- Liu, T.; Inoue, Y.; Shibata, K. A Wearable Ground Reaction Force Sensor System and Its Application to the Measurement of Extrinsic Gait Variability. Sensors 2010, 10, 10240–10255. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, T.; Inoue, Y.; Shibata, K. Development of a Wearable Sensor System for Quantitative Gait Analysis. Measurement 2009, 42, 978–988. [Google Scholar] [CrossRef]
- Schepers, H.M.; Koopman, H.F.J.M.; Veltink, P.H. Ambulatory Assessment of Ankle and Foot Dynamics. IEEE Trans. Biomed. Eng. 2007, 54, 895–902. [Google Scholar] [CrossRef] [Green Version]
- Petrofsky, J.; Lee, S.; Bweir, S. Gait Characteristics in People with Type 2 Diabetes Mellitus. Eur. J. Appl. Physiol. 2005, 93, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Salarian, A.; Russmann, H.; Vingerhoets, F.J.G.; Dehollain, C.; Blanc, Y.; Burkhard, P.R.; Aminian, K. Gait Assessment in Parkinson’s Disease: Toward an Ambulatory System for Long-Term Monitoring. IEEE Trans. Biomed. Eng. 2004, 51, 1434–1443. [Google Scholar] [CrossRef]
- Razian, M.A.; Pepper, M.G. Design, Development, and Characteristics of an in-Shoe Triaxial Pressure Measurement Transducer Utilizing a Single Element of Piezoelectric Copolymer Film. IEEE Trans. Neural Syst. Rehabil. Eng. 2003, 11, 288–293. [Google Scholar] [CrossRef]
- Aminian, K.; Najafi, B.; Büla, C.; Leyvraz, P.-F.; Robert, P. Spatio-Temporal Parameters of Gait Measured by an Ambulatory System Using Miniature Gyroscopes. J. Biomech. 2002, 35, 689–699. [Google Scholar] [CrossRef]
- Huitema, R.B.; Hof, A.L.; Postema, K. Ultrasonic Motion Analysis System—Measurement of Temporal and Spatial Gait Parameters. J. Biomech. 2002, 35, 837–842. [Google Scholar] [CrossRef] [Green Version]
- Miyazaki, S. Long-Term Unrestrained Measurement of Stride Length and Walking Velocity Utilizing a Piezoelectric Gyroscope. IEEE Trans. Biomed. Eng. 1997, 44, 753–759. [Google Scholar] [CrossRef]
- Lee, C.-N.; Fong, V.H.; Chu, Y.-T.; Cheng, L.; Chuang, H.-W.; Lo, C.-Y. A Wearable Device Of Gait Tracking For Parkinson’S Disease Patients. In Proceedings of the 2018 International Conference on Machine Learning and Cybernetics (ICMLC), Chengdu, China, 15–18 July 2018; pp. 462–466. [Google Scholar]
- Gait Abnormalities. Available online: https://stanfordmedicine25.stanford.edu/the25/gait.html (accessed on 21 January 2021).
- Snijders, A.H.; van de Warrenburg, B.P.; Giladi, N.; Bloem, B.R. Neurological Gait Disorders in Elderly People: Clinical Approach and Classification. Lancet Neurol. 2007, 6, 63–74. [Google Scholar] [CrossRef]
- Gras, L.Z.; Kanaan, S.F.; McDowd, J.M.; Colgrove, Y.M.; Burns, J.; Pohl, P.S. Balance and Gait of Adults With Very Mild Alzheimer Disease. J. Geriatr. Phys. Ther. 2015, 38, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Hausdorff, J.M.; Edelberg, H.K.; Mitchell, S.L.; Goldberger, A.L.; Wei, J.Y. Increased Gait Unsteadiness in Community-Dwelling Elderly Fallers. Arch. Phys. Med. Rehabil. 1997, 78, 278–283. [Google Scholar] [CrossRef]
- Kearney, F.C.; Harwood, R.H.; Gladman, J.R.F.; Lincoln, N.; Masud, T. The Relationship between Executive Function and Falls and Gait Abnormalities in Older Adults: A Systematic Review. Dement. Geriatr. Cogn. Disord. 2013, 36, 20–35. [Google Scholar] [CrossRef]
- Laovoravit, T.D.; Stomberg, N.A.; Lam, B.L. MagneForce: Validation of a Modular Tri-Axial Force Sensor for Gait Analysis. Major Qualifying Project Report. Worcester Polytechnic Institute: Worcester, MA, 2017. Available online: https://digital.wpi.edu/concern/student_works/wh246t61d?locale=en (accessed on 9 February 2021).
- Arami, A.; Vida Martins, N.; Aminian, K. Locally Linear Neuro-Fuzzy Estimate of the Prosthetic Knee Angle and Its Validation in a Robotic Simulator. IEEE Sens. J. 2015, 15, 6271–6278. [Google Scholar] [CrossRef] [Green Version]
- Allegro MicroSystems—A1301 and A1302: Continuous-Time Ratiometric Linear Hall Effect Sensor ICs. Available online: https://www.allegromicro.com/en/products/discontinued-product-archive/a1301-2 (accessed on 21 January 2021).
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Olkin, I.; Olkin, I. Contributions to Probability and Statistics; Stanford University Press: Stanford, CA, USA, 1960. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Bulmer, M.G. Principles of Statistics; Dover Publications: Garden City, NY, USA, 1979. [Google Scholar]
- Hoaglin, D.C.; Iglewicz, B.; Tukey, J.W. Performance of Some Resistant Rules for Outlier Labeling. J. Am. Stat. Assoc. 1986, 81, 991–999. [Google Scholar] [CrossRef]
- Allegro MicroSystems: Hall-Effect Sensors Consume Very Little Power. Available online: https://www.eetimes.com/allegro-microsystems-hall-effect-sensors-consume-very-little-power/# (accessed on 9 February 2021).
- Piezo Film Vibration Sensor/Switch. Available online: https://www.te.com/usa-en/product-CAT-PFS0006.html (accessed on 21 January 2021).
- ADXRS290 Datasheet and Product Info |Analog Devices. Available online: https://www.analog.com/en/products/adxrs290.html# (accessed on 21 January 2021).
- MTI-1-T XSens Technologies BV|Sensors, Transducers|DigiKey. Available online: https://www.digikey.com/en/products/detail/xsens-technologies-bv/MTI-1-T/5773873 (accessed on 21 January 2021).
- Pololu—Sharp GP2Y0A41SK0F Analog Distance Sensor 4–30 cm. Available online: https://www.pololu.com/product/2464/specs (accessed on 21 January 2021).
- URM07-UART_Ultrasonic_Sensor_SKU__SEN0153-DFRobot. Available online: https://wiki.dfrobot.com/URM07-UART_Ultrasonic_Sensor_SKU__SEN0153 (accessed on 21 January 2021).
- Inc, I.E. FSR 400. Available online: https://www.interlinkelectronics.com/fsr-400 (accessed on 21 January 2021).
- ADXL202 Datasheet and Product Info|Analog Devices. Available online: https://www.analog.com/en/products/adxl202.html#product-overview (accessed on 21 January 2021).






| Year | Study | Sensors | Worn On | Function |
|---|---|---|---|---|
| 2019 | [29] | IMU | Ft | Measured stride width and stride length |
| 2019 | [30] | A | Ba | Measured toe-off and heel strike timing in the foot |
| 2018 | [31] | IR, IMU, F | Ft | Measured peak foot contact pressure, stance ratio, gait velocity |
| 2017 | [32] | F | Ft | Measured foot clearance for reducing falls among elderly |
| 2017 | [33] | IMG, EMG | L | Measured foot pressure distribution |
| 2017 | [34] | F | Ft | Evaluated gait asymmetry via foot contact pressure data |
| 2015 | [35] | IR | Ft | Measured foot position and orientation |
| 2015 | [36] | A | Ank | Measured multiple temporal gait parameters (e.g., cadence) |
| 2015 | [37] | F | Ft | Measured foot contact pressure during rehabilitation |
| 2015 | [38] | A, G, U | Ft | Measured step length and stride width |
| 2014 | [39] | IMU | S | Detected gait disturbances in Parkinson’s disease patients |
| 2014 | [40] | IMU | H, Ba, L | Detected onset of a turn |
| 2014 | [41] | IMU | Ft, S, Th | Detected gait phases |
| 2013 | [42] | IMU, IR | Ft | Measured step length and stride width |
| 2013 | [43] | G | S | Measured stride length and gait velocity |
| 2013 | [44] | A | W | Detected Parkinsonian step and measure step length |
| 2010 | [45] | F | Ft | Detected abnormal gait using ground contact forces |
| 2009 | [46] | G, A | Ft, L | Detected gait phases |
| 2008 | [19] | A, B, EF, F, G | Ft | Detected gait abnormalities among Parkinson’s disease patients |
| 2007 | [47] | F, IMU | Ft, L | Measured center of pressure, heel position, and ankle moment |
| 2005 | [48] | A, F | A, H, Ft, Sh, W | Detected gait abnormalities among diabetic patients |
| 2004 | [49] | G | Arm, Sh, Th | Detected gait abnormalities in Parkinson’s disease patients |
| 2003 | [50] | F | Ft | Measured sheer and vertical forces in the foot during gait |
| 2002 | [51] | G | Sh, Th | Measured stride length and gait velocity |
| 2002 | [32] | F | Ft | Measured contact pressures and foot contact time for diabetics |
| 2002 | [52] | U | Ft | Measured stance/swing duration and step/stride length |
| 1997 | [53] | F, G | Th | Measured stride length and walking velocity |
| Study | Sensors | Worn | Approach |
|---|---|---|---|
| Bamberg et al. [19] | A, B, EF, F, G | Ft | Pitch, stride length, stride time, and percent stance time used to differentiate normal and Parkinsonian gait |
| Djuric-Jovicic et al. [39] | IMU | S | Rule-based data processing used to detect normal, short, and very short strides as well as freezing of gait in Parkinson’s disease patients |
| Li et al. [31] | IR, IMU, F | Ft | Peak pressure, stance ratio, stride length, walking velocity, and step-time variability used to compare toe-restrained vs. normal gait |
| Liu et al. [45] | F | Ft | Center of pressure and variation in foot contact forces used to detect fast, slow, and normal gait in obstacle and non-obstacle paths |
| Makino et al. [37] | F | Ft | Self-organizing maps (SOM) used to classify narrow vs. wide stride and slow vs. fast walking velocity for characterizing gait abnormality among patients who underwent total knee arthroplasty surgery |
| Petrofsky et al. [48] | A, F | Arm, H, Ft, Sh, W | Stance width and gait velocity found to be significantly different between normal and diabetic gait while walking a straight line and turning |
| Salarian et al. [49] | G | Arm, S, Th | Stride length and gait velocity; stance, double support, and gait cycle times used to detect abnormal gait among Parkinson’s disease patients |
| Yu et al. [30] | A | Ba | Kurtosis, crest factor, and mean stride interval used to distinguish abnormal and normal gait in cerebralspinal mengingitis patients |
| Study | Sensors | Worn | Performance |
|---|---|---|---|
| Cadence/Gait Speed/Gait Velocity | |||
| Aminian et al. [51] | G | S, Th | 0.006 m/sec accuracy relative to FSR reference |
| Lopez-Nava et al. [36] | A | Ank | 4.6% accuracy in measuring cadence relative to GaitRite force/pressure sensing pad |
| Miyazaki et al. [53] | F, G | Th | ±15% accuracy in measuring gait velocity |
| Salarian et al. [43] | G | S | −22.6 cm/s accuracy relative to a force-sensitive platform and a camera-based reference; 7.0 cm/s precision |
| Stride Width | |||
| Hao et al. [29] | IMU | Ft | 0.02 cm accuracy relative to a camera-based reference; 0.95 cm precision |
| Hung et al. [42] | IMU, IR | Ft | 0.4 cm mean accuracy relative to marker reference |
| Liu et al. [45] | F | Ft | 0.64 cm accuracy relative to a camera-based reference and force-sensitive plate reference; 0.1 cm precision |
| Weenk et al. [38] | A, G, U | Ft | 1.2 cm accuracy relative to camera-based reference; 1.2 cm precision |
| Gait Label | Type | Description |
|---|---|---|
| Normal | Normal | Walk at a normal pace, one that requires no conscious attention or focus on the nature or speed of gait. |
| Fast | Abnormal | Walk at a brisk pace, as if in a hurry. |
| Slow | Abnormal | Walk slowly, as if enjoying a sunny day. |
| Right Antalgic | Irregular | Walk in such a way that stance/swing ratio on the right side of the body is smaller than normal gait—by walking with the left shoe off. Simulates a right limp. |
| Left Antalgic | Irregular | Walk in such a way that stance/swing ratio on the left side of the body is smaller than normal gait—by walking with the right shoe off. Simulates a left limp. |
| Type | N | Leg Gap Width (cm) | Skew | Kurtosis | Normal * | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | IQR | Max | Min | |||||
| Subject #1 | |||||||||
| Normal | 37 | 1.53 | 0.046 | 0.057 | 1.61 | 1.44 | −0.24 | 2.33 | Y |
| Fast | 38 | 1.42 | 0.090 | 0.114 | 1.59 | 1.24 | 0.22 | 2.54 | Y |
| Slow | 48 | 1.50 | 0.091 | 0.099 | 1.61 | 1.12 | −1.60 | 5.61 | N |
| AntalgicR | 37 | 1.41 | 0.089 | 0.086 | 1.52 | 1.46 | −1.09 | 3.43 | N |
| AntalgicL | 40 | 1.55 | 0.040 | 0.061 | 1.29 | 1.14 | −0.67 | 2.55 | N |
| Subject #2 | |||||||||
| Normal | 44 | 1.58 | 0.017 | 0.017 | 1.61 | 1.50 | −2.50 | 13.50 | N |
| Fast | 38 | 1.59 | 0.023 | 0.025 | 1.61 | 1.52 | −1.12 | 3.91 | N |
| Slow | 44 | 1.58 | 0.016 | 0.025 | 1.61 | 1.53 | −0.43 | 4.40 | Y |
| AntalgicR | 42 | 1.48 | 0.065 | 0.079 | 1.60 | 1.25 | −1.01 | 5.64 | Y |
| AntalgicL | 46 | 1.55 | 0.048 | 0.036 | 1.61 | 1.37 | −1.60 | 5.86 | N |
| Subject #3 | |||||||||
| Normal | 51 | 1.49 | 0.074 | 0.088 | 1.60 | 1.28 | −0.68 | 3.08 | Y |
| Fast | 41 | 1.47 | 0.072 | 0.093 | 1.62 | 1.29 | −0.25 | 2.91 | Y |
| Slow | 53 | 1.53 | 0.054 | 0.071 | 1.62 | 1.36 | −0.83 | 3.68 | Y |
| AntalgicR | 50 | 1.48 | 0.063 | 0.071 | 1.60 | 1.25 | −0.84 | 5.13 | Y |
| AntalgicL | 49 | 1.51 | 0.050 | 0.064 | 1.61 | 1.38 | −0.55 | 3.18 | Y |
| Subject #4 | |||||||||
| Normal | 38 | 1.53 | 0.044 | 0.064 | 1.61 | 1.41 | −0.46 | 3.26 | Y |
| Fast | 32 | 1.60 | 0.012 | 0.013 | 1.62 | 1.57 | −1.01 | 3.45 | N |
| Slow | 34 | 1.59 | 0.016 | 0.018 | 1.61 | 1.55 | −0.81 | 3.33 | Y |
| AntalgicR | 36 | 1.61 | 0.011 | 0.017 | 1.62 | 1.58 | −0.89 | 3.07 | N |
| AntalgicL | 41 | 1.62 | 0.005 | 0.005 | 1.63 | 1.60 | −3.11 | 17.10 | N |
| Fast Strides | Slow Strides | Right Antalgic | Left Antalgic | All Strides | |||||
|---|---|---|---|---|---|---|---|---|---|
| Subject #1 | |||||||||
| H(1) = 27.53 p = 0.000 | *** | H(1) = 1.93 p = 0.165 | H(1) = 40.08 p = 0.000 | *** | H(1) = 0.34 p = 0.557 | H(4) = 71.46 p = 0.000 | *** | ||
| Subject #2 | |||||||||
| H(1) = 1.71 p = 0.190 | H(1) = 1.42 p = 0.233 | H(1) = 51.48 p = 0.000 | *** | H(1) = 26.49 p = 0.000 | *** | H(4) = 100.52 p = 0.000 | *** | ||
| Subject #3 | |||||||||
| H(1) = 4.19 p = 0.041 | * | H(1)= 7.02 p = 0.008 | ** | H(1) = 2.83 p = 0.093 | H(1) = 1.19 p = 0.276 | H(4) = 33.32 p = 0.000 | *** | ||
| Subject #4 | |||||||||
| H(1) = 44.59 p = 0.000 | *** | H(1) = 34.44 p = 0.000 | *** | H(1) = 50.03 p = 0.000 | *** | H(1) = 58.99 p = 0.000 | *** | H(4) = 135.58 p = 0.000 | *** |
| Fast Strides | Slow Strides | Right Antalgic | Left Antalgic | All Strides | |||||
|---|---|---|---|---|---|---|---|---|---|
| Subject #1 | |||||||||
| H(1) = 10.70 p = 0.001 | ** | H(1) = 2.62 p = 0.105 | H(1) = 16.12 p = 0.000 | *** | H(1) = 9.13 p = 0.003 | ** | H(4) = 55.45 p = 0.000 | *** | |
| Subject #2 | |||||||||
| H(1) = 3.22 p = 0.073 | H(1) = 1.52 p = 0.217 | H(1) = 50.93 p = 0.000 | *** | H(1) = 23.10 p = 0.000 | *** | H(4) = 101.95 p = 0.000 | *** | ||
| Subject #3 | |||||||||
| H(1) = 5.03 p = 0.025 | * | H(1) = 7.35 p = 0.007 | ** | H(1) = 2.98 p = 0.084 | H(1) = 1.63 p = 0.202 | H (4) = 36.92 p = 0.000 | *** | ||
| Subject #4 | |||||||||
| H(1) = 44.83 p = 0.000 | *** | H(1) = 34.64 p = 0.000 | *** | H(1) = 49.97 p = 0.000 | *** | H(1) = 59.23 p = 0.000 | *** | H(4) = 138.14 p = 0.000 | *** |
| Subject | Fast Strides | Slow Strides | Right Antalgic | Left Antalgic | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | F = 14.09 p = 0.0003 | *** | F = 7.28 p = 0.009 | ** | F = 8.04 p = 0.006 | ** | F = 1.19 p = 0.279 | |
| 2 | F = 4.16 p = 0.048 | * | F = 0.34 p = 0.562 | F = 29.89 p = 0.000 | *** | F = 16.79 p = 0.0001 | *** | |
| 3 | F = 0.04 p = 0.844 | F = 3.92 p = 0.051 | F = 1.56 p = 0.214 | F = 5.01 p = 0.028 | * | |||
| 4 | F = 29.31 p = 0.000 | *** | F = 22.56 p = 0.000 | *** | F = 33.73 p = 0.000 | *** | F = 59.24 p = 0.000 | *** |
| Subject | Fast Strides | Slow Strides | Right Antalgic | Left Antalgic | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | F = 14.37 p = 0.0004 | *** | F = 7.42 p = 0.008 | ** | F = 8.82 p = 0.005 | ** | F = 2.09 p = 0..156 | |
| 2 | F = 6.80 p = 0.011 | * | F = 4.15 p = 0.045 | * | F = 49.57 p = 0.000 | *** | F = 16.57 p = 0.000 | *** |
| 3 | F = 0.03 p = 0.87 | F = 4.67 p = 0.033 | * | F = 2.57 p = 0.112 | F = 7.28 p = 0.008 | ** | ||
| 4 | F = 35.84 p = 0.000 | *** | F = 27.19 p = 0.000 | *** | F = 38.99 p = 0.000 | *** | F = 78.45 p = 0.000 | *** |
| Type | Samples | Cadence [Steps/Min] | Skewness | Kurtosis | Normal * | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | IQR | Max | Min | |||||
| Subject #1 | |||||||||
| Normal | 29 | 122.22 | 2.06 | 3.13 | 125.92 | 117.42 | −0.37 | 2.73 | Y |
| Fast | 27 | 127.97 | 3.45 | 2.35 | 133.33 | 116.39 | −2.07 | 7.73 | N |
| Slow | 33 | 100.74 | 2.54 | 3.15 | 105.45 | 95.16 | −0.49 | 2.78 | Y |
| AntalgicR | 30 | 121.15 | 2.32 | 2.68 | 125.66 | 116.73 | 0.25 | 2.47 | Y |
| AntalgicL | 34 | 120.50 | 3.03 | 4.47 | 125.13 | 113.74 | −0.59 | 2.39 | N |
| Subject #2 | |||||||||
| Normal | 41 | 117.15 | 3.64 | 4.12 | 127.52 | 108.11 | 0.39 | 4.36 | Y |
| Fast | 32 | 134.17 | 4.34 | 3.77 | 145.81 | 129.31 | 1.49 | 4.72 | N |
| Slow | 43 | 110.33 | 2.97 | 3.63 | 121.09 | 104.26 | 0.50 | 5.61 | N |
| AntalgicR | 36 | 118.75 | 4.06 | 4.86 | 124.74 | 108.50 | −0.82 | 3.29 | Y |
| AntalgicL | 42 | 119.34 | 2.85 | 2.96 | 126.58 | 112.36 | 0.29 | 3.54 | Y |
| Subject #3 | |||||||||
| Normal | 43 | 110.75 | 3.73 | 4.55 | 117.76 | 101.35 | −0.67 | 3.24 | N |
| Fast | 35 | 119.41 | 4.39 | 4.78 | 132.01 | 111.32 | 0.66 | 3.79 | Y |
| Slow | 48 | 77.44 | 3.30 | 3.57 | 86.15 | 70.01 | −0.24 | 3.33 | Y |
| AntalgicR | 44 | 108.44 | 4.14 | 4.59 | 120.48 | 99.50 | 0.48 | 4.52 | Y |
| AntalgicL | 43 | 107.77 | 4.01 | 4.01 | 115.72 | 99.09 | −0.14 | 2.36 | Y |
| Subject #4 | |||||||||
| Normal | 32 | 118.40 | 2.93 | 4.40 | 123.33 | 111.63 | −0.63 | 2.98 | Y |
| Fast | 26 | 141.06 | 4.72 | 7.40 | 149.25 | 130.72 | −0.24 | 2.43 | Y |
| Slow | 28 | 105.53 | 4.95 | 7.07 | 115.16 | 97.56 | 0.10 | 2.27 | Y |
| AntalgicR | 29 | 125.10 | 4.00 | 6.14 | 132.01 | 115.72 | −0.43 | 2.78 | Y |
| AntalgicL | 35 | 125.26 | 2.53 | 2.98 | 129.31 | 119.28 | −0.46 | 2.88 | Y |
| Subject | Fast Strides | Slow Strides | Right Antalgic | Left Antalgic | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | H (1) = 30.10 p = 0.000 | *** | H (1) = 45.60 p = 0.000 | *** | H (1) = 3.89 p = 0.049 | * | H (1) = 5.03 p = 0.025 | * |
| 2 | H (1) = 53.20 p = 0.000 | *** | H (1) = 47.95 p = 0.000 | *** | H (1) = 5.16 p = 0.023 | * | H (1) = 10.11 p = 0.000 | *** |
| 3 | H (1) = 46.62 p = 0.000 | *** | H (1) = 67.32 p = 0.000 | *** | H (1) = 10.86 p = 0.001 | ** | H (1) = 11.09 p = 0.0009 | *** |
| 4 | H (1) = 42.32 p = 0.000 | *** | H (1) = 41.57 p = 0.000 | *** | H (1) = 31.17 p = 0.000 | *** | H (1) = 43.36 p = 0.000 | *** |
| Subject | Fast Strides | Slow Strides | Right Antalgic | Left Antalgic | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | F = 0.53 p = 0.487 | F = 0.90 p = 0.347 | F = 0.47 p = 0.496 | F = 5.48 p = 0.023 | * | |||
| 2 | F = 0.36 p = 0.551 | F = 0.48 p = 0.402 | F = 1.04 p = 0.312 | F = 0.92 p = 0.341 | ||||
| 3 | F = 0.41 p = 0.524 | F = 9.35 p = 0.493 | F = 0.09 p = 0.763 | F = 0.89 p = 0.345 | ||||
| 4 | F = 7.57 p = 0.008 | ** | F = 6.69 p = 0.0013 | ** | F = 3.33 p = 0.073 | F = 0.65 p = 0.424 | ||
| Parameter (Sensor Type) | Example | Power [mW] 1 | Cost [USD] 4 | Size [cm] 5 | Weight [g] |
|---|---|---|---|---|---|
| Bending/Vibration (PVDF Strips) | TE Connectivity LDT0 [69] used in [19] | NA | $2.69 | 2.5 × 1.3 | NA |
| Angular rate, orientation (gyroscope) | Analog Devices ADXRS290 similar to ADXRS150 [70] used in [19] | 39 (0.4) 2 | $16.06 | 0.6 × 0.4 | NA |
| Acceleration, angular rate, orientation (IMU) | XSens MTi-1 [71] | 45 | $139 | 1.2 × 1.2 | 0.66 |
| Distance (Hall effect) | Allegro 139X [68] replacement for sensors used here | 9.6 (0.08) 2 | $1.20 | 0.8 × 0.3 | 0.014 |
| Distance (Infrared IR) | Sharp GP2YOA41SKOF [72] used in [61] | 60 | $9.93 | 4.4 × 1.9 | 3.5 |
| Distance (Ultrasonic) | URM07 [73] | 25 (0.07) 2 | $5.59 | 2.7 × 2.7 | 4.2 |
| Force/Pressure (Force-Sensitive Resistor) | FSR-400 [74] used in [19] | 2.5 3 | $4.40 | 4.0 × 4.0 | NA |
| Linear Acceleration (accelerometer) | Analog Devices ADXL202E [75] used in [19] | 3.0 | $19.72 | 0.7 × 0.7 | 5 |
| Object Presence (electric field sensors) | Motorola MC33794DH [71] used in [19] | 98 | $24 (est) | 1.6 × 1.1 | NA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chheng, C.; Wilson, D. Abnormal Gait Detection Using Wearable Hall-Effect Sensors. Sensors 2021, 21, 1206. https://doi.org/10.3390/s21041206
Chheng C, Wilson D. Abnormal Gait Detection Using Wearable Hall-Effect Sensors. Sensors. 2021; 21(4):1206. https://doi.org/10.3390/s21041206
Chicago/Turabian StyleChheng, Courtney, and Denise Wilson. 2021. "Abnormal Gait Detection Using Wearable Hall-Effect Sensors" Sensors 21, no. 4: 1206. https://doi.org/10.3390/s21041206
APA StyleChheng, C., & Wilson, D. (2021). Abnormal Gait Detection Using Wearable Hall-Effect Sensors. Sensors, 21(4), 1206. https://doi.org/10.3390/s21041206