Horizontal-to-Vertical Spectral Ratio of Ambient Vibration Obtained with Hilbert–Huang Transform
Abstract
:1. Introduction
2. Methodology
2.1. Multivariate Empirical Mode Decomposition (MEMD)
- Copy time series , initialize mode index () and choose a sifting tolerance (e.g., ).
- Copy the time series .
- Compute cubic splines through maxima and minima of c, these are the envelopes and .
- Obtain the mean of the envelopes and subtract from c.
- Continue if is zero (up to a tolerance), otherwise return to point 3.
- Save current c (from which you repeatedly subtracted ) as IMF with : . Then subtract current IMF from to obtain the new, reduced time series
- If has 3 or fewer extrema continue, otherwise return to point 2.
- Save as residual: .
2.2. Robust, Weighted Statistics for HVSR Processing on a Logarithmic Scale
2.2.1. Preliminaries
2.2.2. HVSR Processing Scheme
2.3. Comparison between FFT- and MEMD-Based HVSR Results
3. Examples
3.1. Tests at the Station ICJA at Geoscience Barcelona, Spain
3.1.1. Introduction and A-Priori Information
3.1.2. Data Preparation and Processing
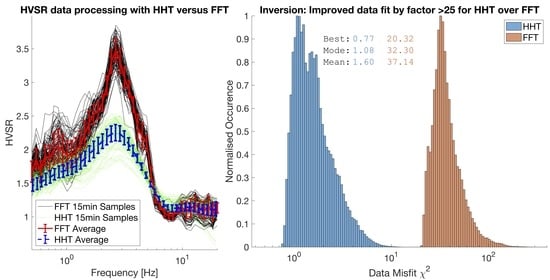
3.1.3. Inversion and Comparison
3.2. Tests at the Station EJDN in a Rural Area of El Ejido (Almería, Spain)
3.2.1. Introduction and A-Priori Information
3.2.2. Data Preparation and Processing
3.2.3. Inversion and Comparison
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HVSR | Horizontal-to-Vertical Spectral Ratio |
| Shear wave velocity | |
| FFT | Fast Fourier Transform |
| HHT | Hilbert–Huang Transform |
| 3C | Three-component |
| (M)EMD | (Multivariate) Empirical Mode Decomposition |
| ISP | Instantaneous spectral parameters |
| DQ | Direct quadrature |
| MAD | Mean average deviation (to the mean) |
| SRD | Square root deviation |
References
- Nakamura, Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Railw. Tech. Res. Inst. Q. Rep. 1989, 30, 25–33. [Google Scholar]
- Bonnefoy-Claudet, S.; Cornou, C.; Bard, P.Y.; Cotton, F.; Moczo, P.; Kristek, J.; Fäh, D. H/V ratio: A tool for site effects evaluation. Results from 1-D noise simulations. Geophys. J. Int. 2006, 167, 827–837. [Google Scholar] [CrossRef] [Green Version]
- Lunedei, E.; Malischewsky, P. A Review and Some New Issues on the Theory of the H/V Technique for Ambient Vibrations (Chapter 15). In Perspectives on European Earthquake Engineering and Seismology; Springer: Berlin/Heidelberg, Germany, 2015; pp. 371–394. [Google Scholar]
- Ugalde, A.; Egozcue, J.J.; Ranero, C.R. A new autoregressive moving average modeling of H/V spectral ratios to estimate the ground resonance frequency. Eng. Geol. 2021, 280. [Google Scholar] [CrossRef]
- García-Jerez, A.; Seivane, H.; Navarro, M.; Martínez-Segura, M.; Piña-Flores, J. Joint analysis of Rayleigh-wave dispersion curves and diffuse-field HVSR for site characterization: The case of El Ejido town (SE Spain). Soil Dyn. Earthq. Eng. 2019, 121, 102–120. [Google Scholar]
- Tumurbaatar, Z.; Miura, H.; Tsamba, T. Site effect assessment in Ulaanbaatar, Mongolia through inversion analysis of microtremor H/V spectral ratios. Geoscience 2019, 9, 228. [Google Scholar] [CrossRef] [Green Version]
- Tian, B.; Du, Y.; You, Z.; Zhang, R. Measuring the sediment thickness in urban areas using revised H/V spectral ratio method. Eng. Geol. 2019, 260, 105223. [Google Scholar] [CrossRef]
- Spica, Z.J.; Perton, M.; Martin, E.R.; Beroza, G.C.; Biondi, B. Urban Seismic Site Characterization by Fiber-Optic Seismology. Sci. Adv. 2020, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Mi, B.; Hu, Y.; Xia, J.; Socco, L.V. Estimation of horizontal-to-vertical spectral ratios (ellipticity) of Rayleigh waves from multistation active-seismic records. Geophysics 2019, 84, EN81–EN92. [Google Scholar] [CrossRef]
- Hloupis, G.; Vallianatos, F.; Stonham, J. A wavelet representation of HVSR. Bull. Geol. Soc. Greece 2004, 36, 1269–1278. [Google Scholar] [CrossRef]
- Carniel, R.; Malisan, P.; Barazza, F.; Grimaz, S. Improvement of HVSR technique by wavelet analysis. Soil Dyn. Earthq. Eng. 2008, 28, 321–327. [Google Scholar]
- Liu, L.; Mehl, R.; Wang, W.; Chen, Q.F. Applications of the Hilbert-Huang transform for microtremor data analysis enhancement. J. Earth Sci. 2015, 26, 799–806. [Google Scholar] [CrossRef]
- Harsuko, M.R.C.; Zulfakriza, Z.; Nugraha, A.D.; Sarjan, A.F.N.; Widiyantoro, S.; Rosalia, S.; Puspito, N.T.; Sahara, D.P. Investigation of Hilbert–Huang Transform and Fourier Transform for Horizontal-to-Vertical Spectral Ratio Analysis: Understanding the Shallow Structure in Mataram City, Lombok, Indonesia. Front. Earth Sci. 2020, 8. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Snin, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rai, V.K.; Mohanty, A.R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform. Mech. Syst. Signal Process. 2007, 21, 2607–2615. [Google Scholar] [CrossRef]
- Jackson, L.P.; Mound, J.E. Geomagnetic variation on decadal time scales: What can we learn from Empirical Mode Decomposition? Geophys. Res. Lett. 2010, 37, 1–6. [Google Scholar] [CrossRef]
- Gairola, G.S.; Chandrasekhar, E. Heterogeneity analysis of geophysical well-log data using Hilbert–Huang transform. Phys. A Stat. Mech. Its Appl. 2017, 478, 131–142. [Google Scholar] [CrossRef]
- Zhu, C.; Cotton, F.; Pilz, M. Detecting Site Resonant Frequency Using HVSR: Fourier versus Response Spectrum and the First versus the Highest Peak Frequency. Bull. Seismol. Soc. Am. 2020, 1–14. [Google Scholar] [CrossRef]
- Horike, M.; Zhao, B.; Kawase, H. Comparison of site response characteristics inferred from microtremors and earthquake shear waves. Bull. Seismol. Soc. Am. 2001, 91, 1526–1536. [Google Scholar]
- Mucciarelli, M.; Gallipoli, M.R.; Arcieri, M. The stability of the horizontal-to-vertical spectral ratio of triggered noise and earthquake recordings. Bull. Seismol. Soc. Am. 2003, 93, 1407–1413. [Google Scholar]
- Parolai, S.; Picozzi, M.; Strollo, A.; Pilz, M.; Di Giacomo, D.; Liss, B.; Bindi, D. Are Transients Carrying Useful Information for Estimating H/V Spectral Ratios? In Increasing Seismic Safety by Combining Engineering Technologies and Seismological Data; Mucciarelli, M., Herak, M., Cassidy, J., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 17–31. [Google Scholar]
- Rodriguez, V.H.; Midorikawa, S. Applicability of the H/V spectral ratio of microtremors in assessing site effects on seismic motion. Earthq. Eng. Struct. Dyn. 2002, 31, 261–279. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Luzio, D.; Martorana, R.; Capizzi, P. Selection of time windows in the horizontal-to-vertical noise spectral ratio by means of cluster analysis. Bull. Seismol. Soc. Am. 2016, 106, 560–574. [Google Scholar] [CrossRef]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- Candra, A.D.; Suryani, P.E. Application of Multivariate Empirical Mode Decomposition to Noise Reduction in Seismic Signal. J. Phys. Conf. Ser. 2019, 1204. [Google Scholar] [CrossRef]
- Neukirch, M.; Garcia, X. Nonstationary magnetotelluric data processing with instantaneous parameter. J. Geophys. Res. Solid Earth 2014, 119. [Google Scholar] [CrossRef] [Green Version]
- Goncalves, P.; Rilling, G.; Flandrin, P. On empirical mode decomposition and its algorithms. IEEE-EURASIP Workshop Nonlinear Signal Image Process. 2003, 3, 8–11. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z.; Long, S.R.; Arnold, K.C.; Chen, X.; Blank, K. On Instantaneous Frequency. Adv. Adapt. Data Anal. 2009, 1, 177–229. [Google Scholar] [CrossRef]
- Galassi, M.; Davies, J.; Theiler, J.; Gough, B.; Jungman, G.; Alken, P.; Booth, M.; Rossi, F.; Ulerich, R. GNU Scientific Library, Reference Manual Version 1.15. 2015. Available online: http://www.gnu.org/software/gsl (accessed on 12 November 2020).
- Neukirch, M.; Garcia, X. On the effect of non stationary (synthetic) sources in the magnetotelluric method. In EGU General Assembly Conference Abstracts; Copernicus Gesellschaft mbH: Göttingen, Germany, 2013; p. EGU2013-10590. Available online: https://cdn.egu.eu/media/awards/union-osp-award/2013/maik_neukirch.pdf (accessed on 8 May 2021).
- Diaz, J.; Pulgar, J.A. MISTERIOS. 2015. Available online: http://www.fdsn.org/networks/detail/2M_2015/ (accessed on 8 May 2021).
- Díaz, J.; Ruiz, M.; Sánchez-Pastor, P.S.; Romero, P. Urban Seismology: On the origin of earth vibrations within a city. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diaz, J.; Ruiz, M.; Jara, J.A. Seismic monitoring of urban activity in Barcelona during the COVID-19 lockdown. Solid Earth 2021, 12, 725–739. [Google Scholar]
- Teixido, T.; Jurado, M.J. Tomografía sísmica vertical inversa 2.5D alrededor del sondeo científico Almera-1, ICTJA-CSIC, Barcelona. IX Congr. Geol. Esp. 2016, 16, 609–612. [Google Scholar]
- Jurado, M.J.; Salvany, J.M. Scientific drilling in the campus: Almera-1 borehole, unraveling urban subsurface geology in Barcelona (Spain). Perforación científica en el campus: Almera-1 un sondeo para investigación del subsuelo urbano Llobregat delta. IX Congr. Geol. Esp. 2016, 16, 617–620. [Google Scholar]
- Wathelet, M.; Chatelain, J.L.; Cornou, C.; Giulio, G.D.; Guillier, B.; Ohrnberger, M.; Savvaidis, A. Geopsy: A User-Friendly Open- Source Tool Set for Ambient Vibration Processing. Seismol. Res. Lett. 2020, 91, 1878–1889. [Google Scholar] [CrossRef]
- SESAME. Guidelines for the Implementation of the H/V Spectral Ratio Technique on Ambient Vibrations-Measurements, Processing and Interpretations, SESAME European Research Project EVG1-CT-2000-00026, Deliverable D23.12; Technical Report; European Commission: Brussels, Belgium, 2004. [Google Scholar]
- Konno, K.; Ohmachi, T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar]
- García-Jerez, A.; Piña-Flores, J.; Sánchez-Sesma, F.J.; Luzón, F.; Perton, M. A computer code for forward calculation and inversion of the H/V spectral ratio under the diffuse field assumption. Comput. Geosci. 2016, 97, 67–78. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Sesma, F.J.; Rodríguez, M.; Iturrarán-Viveros, U.; Luzón, F.; Campillo, M.; Margerin, L.; García-Jerez, A.; Suarez, M.; Santoyo, M.A.; Rodríguez-Castellanos, A. A theory for microtremor H/V spectral ratio: Application for a layered medium. Geophys. J. Int. 2011, 186, 221–225. [Google Scholar] [CrossRef] [Green Version]
- Piña-Flores, J.; Perton, M.; García-Jerez, A.; Carmona, E.; Luzón, F.; Molina-Villegas, J.C.; Sánchez-Sesma, F.J. The inversion of spectral ratio H/V in a layered system using the diffuse field assumption (DFA). Geophys. J. Int. 2017, 208, 577–588. [Google Scholar] [CrossRef]
- Mulargia, F. The seismic noise wavefield is not diffuse. J. Acoust. Soc. Am. 2012, 131, 2853–2858. [Google Scholar] [CrossRef]
- Piña-Flores, J.; Cárdenas-Soto, M.; García-Jerez, A.; Campillo, M.; Sánchez-Sesma, F. The Search of Diffusive Properties in Ambient Seismic Noise. Bull. Seismol. Soc. Am. 2021, in press. [Google Scholar] [CrossRef]
- Sax, R.L. Stationarity of Seismic Noise. Geophysics 1968, 33, 668–674. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Nie, P. A study on the Gaussianity and stationarity of the random noise in the seismic exploration. J. Appl. Geophys. 2014, 109, 210–217. [Google Scholar] [CrossRef]
- Bonnefoy-Claudet, S. Nature du bruit de fond sismique: Implications pour les études des effets de site. Ph.D. Thesis, Université Joseph-Fourier, Grenoble, France, 2004. [Google Scholar]








| Top | Starting Model Vs [m/s] | FFT Vs [m/s] | MEMD Vs [m/s] | ||||
|---|---|---|---|---|---|---|---|
| Lithology | [m] | ± | Bounds | ± | ± | ||
| Foundation | 0.0 | 1700 ± 400 | 50 to 4000 | 1440 | 1200 ± 180 | 1490 | 1510 ± 170 |
| Silt, Sand | 2.5 | 1000 ± 300 | 50 to 4000 | 1000 | 780 ± 110 | 920 | 960 ± 90 |
| Clay, Sand | 28.0 | 1000 ± 300 | 50 to 4000 | 920 | 820 ± 70 | 940 | 1000 ± 70 |
| Weath. Sl. | 41.0 | 900 ± 300 | 50 to 4000 | 810 | 850 ± 90 | 990 | 1020 ± 130 |
| Slate. | 47.0 | 1300 ± 300 | 50 to 4000 | 1260 | 1240 ±60 | 1160 | 1220 ± 50 |
| Schist | 77.5 | 2500 ± 500 | 50 to 4000 | 2790 | 2490 ± 340 | 2330 | 2350 ± 300 |
| Slate | 90.5 | 1300 ± 300 | 50 to 4000 | 1750 | 1220 ± 280 | 1080 | 1270 ± 220 |
| Limestone | 108.5 | 2500 ± 500 | 50 to 4000 | 2500 | 2160 ± 360 | 1940 | 2030 ± 280 |
| Slate | 138.5 | 1600 ± 500 | 50 to 4000 | 1750 | 1720 ± 220 | 1580 | 1720 ± 130 |
| Hornfels | 188.0 | 2500 ± 500 | 50 to 4000 | 3430 | 2640 ± 430 | 2530 | 2650 ± 270 |
| Slate | 202.5 | 2000 ± 500 | 50 to 4000 | 2690 | 2050 ± 280 | 1790 | 2010 ± 240 |
| Depth [m] | Vs [m/s] | |||
|---|---|---|---|---|
| Lithology | ± | Bounds | ± | Bounds |
| Conglomerate, Sand, Silt and Clay | 5 ± 2 | 0 to 10 | 500 ± 100 | 200 to 3500 |
| 14 ± 6 | 0 to 30 | 1050 ± 250 | 200 to 3500 | |
| Sand and Gravel | 30 ± 9 | 0 to 150 | 800 ± 200 | 200 to 3500 |
| Sand and Marl | 170 ± 0 | fixed at 170 | 1150 ± 350 | 200 to 3500 |
| Calcarenite | 264 ± 0 | fixed at 264 | 1300 ± 400 | 200 to 3500 |
| Limestone & Dolomite | 950 ± 150 | 700 to 1200 | 1700 ± 500 | 200 to 3500 |
| Basement | NA | 2200 ± 500 | 200 to 3500 | |
| Lithology | [m] | [m/s] | ± [m] | ± [m/s] |
|---|---|---|---|---|
| Conglomerate, Sand, Silt and Clay | 4.2 | 536 | 4.6 ± 0.8 | 510 ± 48 |
| 6.7 | 946 | 18.3 ± 8.2 | 1017 ± 121 | |
| Sand and Gravel | 43.9 | 1046 | 40.5 ± 10.0 | 847 ± 169 |
| Sand and Marl | 170.0 | 869 | 170.0 ± 0.0 | 922 ± 93 |
| Calcarenite | 264.0 | 1258 | 264.0 ± 0.0 | 1204 ± 117 |
| Limestone & Dolomite | 709.8 | 1703 | 802.1 ± 149.5 | 1655 ± 138 |
| Basement | NA | 2061 | NA | 1839 ± 259 |
| Lithology | [m] | [m/s] | ± [m] | ± [m/s] |
|---|---|---|---|---|
| Conglomerate, Sand, Silt and Clay | 3.3 | 344 | 3.1 ± 0.2 | 348 ± 101 |
| 30.0 | 767 | 27.3 ± 3.1 | 755 ± 56 | |
| Sand and Gravel | 47.3 | 1069 | 44.4 ± 7.4 | 1254 ± 334 |
| Sand and Marl | 170.0 | 992 | 170.0 ± 0.0 | 940 ± 50 |
| Calcarenite | 264.0 | 1148 | 264.0 ± 0.0 | 1279 ± 124 |
| Limestone & Dolomite | 720.1 | 1744 | 793.2 ± 112.9 | 1724 ± 164 |
| Basement | NA | 1994 | NA | 1893 ± 266 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neukirch, M.; García-Jerez, A.; Villaseñor, A.; Luzón, F.; Ruiz, M.; Molina, L. Horizontal-to-Vertical Spectral Ratio of Ambient Vibration Obtained with Hilbert–Huang Transform. Sensors 2021, 21, 3292. https://doi.org/10.3390/s21093292
Neukirch M, García-Jerez A, Villaseñor A, Luzón F, Ruiz M, Molina L. Horizontal-to-Vertical Spectral Ratio of Ambient Vibration Obtained with Hilbert–Huang Transform. Sensors. 2021; 21(9):3292. https://doi.org/10.3390/s21093292
Chicago/Turabian StyleNeukirch, Maik, Antonio García-Jerez, Antonio Villaseñor, Francisco Luzón, Mario Ruiz, and Luis Molina. 2021. "Horizontal-to-Vertical Spectral Ratio of Ambient Vibration Obtained with Hilbert–Huang Transform" Sensors 21, no. 9: 3292. https://doi.org/10.3390/s21093292
APA StyleNeukirch, M., García-Jerez, A., Villaseñor, A., Luzón, F., Ruiz, M., & Molina, L. (2021). Horizontal-to-Vertical Spectral Ratio of Ambient Vibration Obtained with Hilbert–Huang Transform. Sensors, 21(9), 3292. https://doi.org/10.3390/s21093292