Deep-Learning-Based Algorithm for the Removal of Electromagnetic Interference Noise in Photoacoustic Endoscopic Image Processing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data source
2.2. Data Preparation
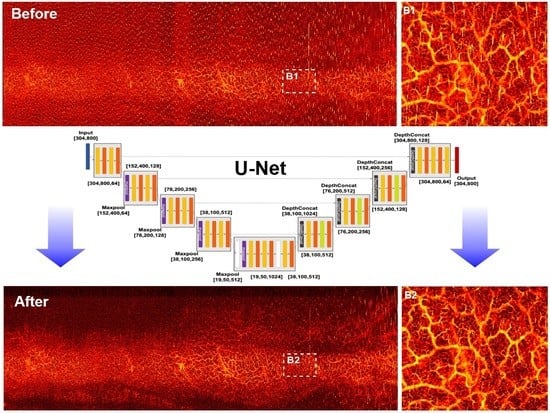
2.3. CNN Architectures
2.4. CNN Training and Hyperparameter Tuning
3. Results
3.1. Performance Comparison of Trained CNN Architectures
3.2. Performance Test for New In Vivo Data
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Middleton, D. Statistical-Physical Models of Electromagnetic Interference. IEEE Trans. Electromagn. Compat. 1977, EMC-19, 106–127. [Google Scholar] [CrossRef]
- Shahparnia, S.; Ramahi, O.M. Electromagnetic Interference (EMI) Reduction from Printed Circuit Boards (PCB) Using Electromagnetic Bandgap Structures. IEEE Trans. Electromagn. Compat. 2004, 46, 580–587. [Google Scholar] [CrossRef]
- Tarateeraseth, V.; See, K.Y.; Canavero, F.G.; Chang, R.W.-Y. Systematic Electromagnetic Interference Filter Design Based on Information from In-Circuit Impedance Measurements. IEEE Trans. Electromagn. Compat. 2010, 52, 588–598. [Google Scholar] [CrossRef] [Green Version]
- Baisden, A.C.; Boroyevich, D.; Wang, F. Generalized Terminal Modeling of Electromagnetic Interference. IEEE Trans. Ind. Appl. 2010, 46, 2068–2079. [Google Scholar] [CrossRef] [Green Version]
- Kaur, M.; Kakar, S.; Mandal, D. Electromagnetic Interference. In Proceedings of the 2011 3rd International Conference on Electronics Computer Technology, Kanyakumari, India, 8–10 April 2011. [Google Scholar]
- Murakawa, K.; Hirasawa, N.; Ito, H.; Ogura, Y. Electromagnetic Interference Examples of Telecommunications System in the Frequency Range From 2kHz to 150kHz. In Proceedings of the 2014 International Symposium on Electromagnetic Compatibility, Tokyo, Japan, 12–16 May 2014. [Google Scholar]
- Sankaran, S.; Deshmukh, K.; Ahamed, M.B.; Pasha, S.K.K. Recent Advances in Electromagnetic Interference Shielding Properties of Metal and Carbon Filler Reinforced Flexible Polymer Composites: A Review. Compos. A Appl. Sci. Manuf. 2018, 114, 49–71. [Google Scholar] [CrossRef]
- Beard, P. Biomedical Photoacoustic Imaging. Interface Focus 2011, 1, 602–631. [Google Scholar] [CrossRef]
- Wang, L.H.V.; Hu, S. Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs. Science 2012, 335, 1458–1462. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Wang, L.V. Sensitivity of Photoacoustic Microscopy. Photoacoustics 2014, 2, 87–101. [Google Scholar] [CrossRef] [Green Version]
- Weber, J.; Beard, P.C.; Bohndiek, S.E. Contrast Agents for Molecular Photoacoustic Imaging. Nat. Methods 2016, 13, 639–650. [Google Scholar] [CrossRef] [Green Version]
- Dean-Ben, X.L.; Gottschalk, S.; Mc Larney, B.; Shoham, S.; Razansky, D. Advanced Optoacoustic Methods for Multiscale Imaging of In Vivo Dynamics. Chem. Soc. Rev. 2017, 46, 2158–2198. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.; Duan, T.; Lan, H.; Zhou, M.; Gao, F. Review of Low-Cost Photoacoustic Sensing and Imaging Based on Laser Diode and Light-Emitting Diode. Sensors 2018, 18, 2264. [Google Scholar] [CrossRef] [Green Version]
- Jeon, S.; Kim, J.; Lee, D.; Baik, J.W.; Kim, C. Review on Practical Photoacoustic Microscopy. Photoacoustics 2019, 15, 100141. [Google Scholar] [CrossRef]
- Omar, M.; Aguirre, J.; Ntziachristos, V. Optoacoustic Mesoscopy for Biomedicine. Nat. Biomed. Eng. 2019, 3, 354–370. [Google Scholar] [CrossRef]
- Yang, J.-M.; Ghim, C.M. Photoacoustic Tomography Opening New Paradigms in Biomedical Imaging. Adv. Exp. Med. Biol. 2021, 1310, 239–341. [Google Scholar]
- Wu, M.; Awasthi, N.; Rad, N.M.; Pluim, J.P.W.; Lopata, R.G.P. Advanced Ultrasound and Photoacoustic Imaging in Cardiology. Sensors 2021, 21, 7947. [Google Scholar] [CrossRef]
- Oraevsky, A.A.; Esenaliev, R.O.; Karabutov, A.A. Laser Optoacoustic Tomography of Layered Tissue: Signal Processing. Proc. SPIE 1997, 2979, 59–70. [Google Scholar]
- Yang, J.-M.; Maslov, K.; Yang, H.C.; Zhou, Q.; Shung, K.K.; Wang, L.V. Photoacoustic Endoscopy. Opt. Lett. 2009, 34, 1591–1593. [Google Scholar] [CrossRef]
- Yang, J.-M.; Favazza, C.; Chen, R.; Yao, J.; Cai, X.; Maslov, K.; Zhou, Q.; Shung, K.K.; Wang, L.V. Simultaneous Functional Photoacoustic and Ultrasonic Endoscopy of Internal Organs In Vivo. Nat. Med. 2012, 18, 1297–1302. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.-M.; Li, C.; Chen, R.; Rao, B.; Yao, J.; Yeh, C.-H.; Danielli, A.; Maslov, K.; Zhou, Q.; Shung, K.K. Optical-Resolution Photoacoustic Endomicroscopy In Vivo. Biomed. Opt. Express 2015, 6, 918–932. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Lin, R.; Liu, C.; Chen, J.; Liu, H.; Zheng, R.; Gong, X.; Song, L. In Vivo Photoacoustic/Ultrasonic Dual-Modality Endoscopy with a Miniaturized Full Field-of-View Catheter. J. Biophotonics 2018, 11, e201800034. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Jing, J.C.; Chen, J.J.; Heidari, E.; He, Y.; Zhu, J.; Ma, T.; Yu, M.; Zhou, Q. High-Speed Integrated Endoscopic Photoacoustic and Ultrasound Imaging System. IEEE J. Sel. Top. Quantum. Electron. 2019, 25, 7102005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bai, X.; Gong, X.; Hau, W.; Lin, R.; Zheng, J.; Liu, C.; Zeng, C.; Zou, X.; Zheng, H.; Song, L. Intravascular Optical-Resolution Photoacoustic Tomography with a 1.1 mm Diameter Catheter. PLoS ONE 2014, 9, e92463. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, M.; Springeling, G.; Lovrak, M.; Mastik, F.; Iskander-Rizk, S.; Wang, T.; Van Beusekom, H.M.M.; Van der Steen, A.F.W.; Van Soest, G. Real-Time Volumetric Lipid Imaging In Vivo by Intravascular Photoacoustics at 20 Frames per Second. Biomed. Opt. Express 2017, 8, 943–953. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Kole, A.; Hui, J.; Zhang, Y.; Mai, J.; Alloosh, M.; Sturek, M.; Cheng, J.-X. Fast Assessment of Lipid Content in Arteries In Vivo by Intravascular Photoacoustic Tomography. Sci. Rep. 2018, 8, 2400. [Google Scholar] [CrossRef]
- Lin, L.; Xie, Z.; Xu, M.; Wang, Y.; Li, S.; Yang, N.; Gong, X.; Liang, P.; Zhang, X.; Song, L. IVUS\IVPA Hybrid Intravascular Molecular Imaging of Angiogenesis in Atherosclerotic Plaques via RGDfk Peptide-Targeted Nanoprobes. Photoacoustics 2021, 22, 100262. [Google Scholar] [CrossRef]
- Leng, J.; Zhang, J.; Li, C.; Shu, C.; Wang, B.; Lin, R.; Liang, Y.; Wang, K.; Shen, L.; Lam, K.H. Multi-Spectral Intravascular Photoacoustic/Ultrasound/Optical Coherence Tomography Tri-Modality System with a Fully-Integrated 0.9-mm Full Field-of-View Catheter for Plaque Vulnerability Imaging. Biomed. Opt. Express 2021, 12, 1934–1946. [Google Scholar] [CrossRef]
- Kim, M.; Lee, K.W.; Kim, K.S.; Gulenko, O.; Lee, C.; Keum, B.; Chun, H.J.; Choi, H.S.; Kim, C.U.; Yang, J.-M. Intra-Instrument Channel Workable, Optical-Resolution Photoacoustic and Ultrasonic Mini-Probe System for Gastrointestinal Endoscopy. Photoacoustics 2022, 26, 100346. [Google Scholar] [CrossRef]
- Song, Z.; Fu, Y.; Qu, J.; Liu, Q.; Wei, X. Application of Convolutional Neural Network in Signal Classification for In Vivo Photoacoustic Flow Cytometry. Proc. SPIE 2020, 11553, 115532W. [Google Scholar]
- Zhang, J.; Chen, B.; Zhou, M.; Lan, H.; Gao, F. Photoacoustic Image Classification and Segmentation of Breast Cancer: A Feasibility Study. IEEE Access 2019, 7, 5457–5466. [Google Scholar] [CrossRef]
- Shan, H.; Wang, G.; Yang, Y. Accelerated Correction of Reflection Artifacts by Deep Neural Networks in Photo-Acoustic Tomography. Appl. Sci. 2019, 9, 2615. [Google Scholar] [CrossRef] [Green Version]
- Tong, T.; Huang, W.; Wang, K.; He, Z.; Yin, L.; Yang, X.; Zhang, S.; Tian, J. Domain Transform Network for Photoacoustic Tomography from Limited-view and Sparsely Sampled Data. Photoacoustics 2020, 19, 100190. [Google Scholar] [CrossRef]
- DiSpirito, A.; Li, D.; Vu, T.; Chen, M.; Zhang, D.; Luo, J.; Horstmeyer, R.; Yao, J. Reconstructing Undersampled Photoacoustic Microscopy Images Using Deep Learning. IEEE Trans. Med. Imaging 2021, 40, 562–570. [Google Scholar] [CrossRef]
- Guan, S.; Khan, A.A.; Sikdar, S.; Chitnis, P.V. Fully Dense UNet for 2-D Sparse Photoacoustic Tomography Artifact Removal. IEEE J. Biomed. Health Inform. 2020, 24, 568–576. [Google Scholar] [CrossRef] [Green Version]
- Godefroy, G.; Arnal, B.; Bossy, E. Compensating for Visibility Artefacts in Photoacoustic Imaging with a Deep Learning Approach Providing Prediction Uncertainties. Photoacoustics 2021, 21, 100218. [Google Scholar] [CrossRef]
- Chen, X.; Qi, W.; Xi, L. Deep-Learning-Based Motion-Correction Algorithm in Optical Resolution Photoacoustic Microscopy. Vis. Comput. Ind. Biomed. Art 2019, 2, 12. [Google Scholar] [CrossRef]
- Lan, H.; Jiang, D.; Yang, C.; Gao, F.; Gao, F. Y-Net: Hybrid Deep Learning Image Reconstruction for Photoacoustic Tomography In Vivo. Photoacoustics 2020, 20, 100197. [Google Scholar] [CrossRef]
- Davoudi, N.; Deán-Ben, X.L.; Razansky, D. Deep Learning Optoacoustic Tomography with Sparse Data. Nat. Mach. Intell. 2019, 1, 453–460. [Google Scholar] [CrossRef]
- Ly, C.D.; Nguyen, V.T.; Vo, T.H.; Mondal, S.; Park, S.; Choi, J.; Vu, T.T.H.; Kim, C.-S.; Oh, J. Full-View In Vivo Skin and Blood Vessels Profile Segmentation in Photoacoustic Imaging Based on Deep Learning. Photoacoustics 2022, 25, 100310. [Google Scholar] [CrossRef]
- Chlis, N.-K.; Karlas, A.; Fasoula, N.-A.; Kallmayer, M.; Eckstein, H.-H.; Theis, F.J.; Ntziachristos, V.; Marr, C. A sparse deep learning approach for automatic segmentation of human vasculature in multispectral optoacoustic tomography. Photoacoustics 2020, 20, 100203. [Google Scholar] [CrossRef]
- Lafci, B.; Merčep, E.; Morscher, S.; Deán-Ben, X.L.; Razansky, D. Deep Learning for Automatic Segmentation of Hybrid Optoacoustic Ultrasound (OPUS) Images. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 688–696. [Google Scholar] [CrossRef]
- Hariri, A.; Alipour, K.; Mantri, Y.; Schulze, J.P.; Jokerst, J.V. Deep Learning Improves Contrast in Low-Fluence Photoacoustic Imaging. Biomed. Opt. Express 2020, 11, 3360–3373. [Google Scholar] [CrossRef] [PubMed]
- Awasthi, N.; Jain, G.; Kalva, S.K.; Pramanik, M.; Yalavarthy, P.K. Deep Neural Network-Based Sinogram Super-Resolution and Bandwidth Enhancement for Limited-Data Photoacoustic Tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 2660–2673. [Google Scholar] [CrossRef] [PubMed]
- Chan, R.H.; Ho, C.-W.; Nikolova, M. Salt-And-Pepper Noise Removal by Median-Type Noise Detectors and Detail-Preserving Regularization. IEEE Trans. Image Process. 2005, 14, 1479–1485. [Google Scholar] [CrossRef] [PubMed]
- Patidar, P.; Srivastava, S. Image De-noising by Various Filters for Different Noise. Int. J. Comput. Appl. 2010, 9, 45–50. [Google Scholar] [CrossRef]
- Verma, R.; Ali, J.A. Comparative Study of Various Types of Image Noise and Efficient Noise Removal Techniques. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 617–622. [Google Scholar]
- Fan, L.; Zhang, F.; Fan, H.; Zhang, C. Brief Review of Image Denoising Techniques. Vis. Comput. Ind. Biomed. Art 2019, 2, 7. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Ye, J.C.; De Man, B. Deep Learning for Tomographic Image Reconstruction. Nat. Mach. Intell. 2020, 2, 737–748. [Google Scholar] [CrossRef]
- Hauptmann, A.; Cox, B.T. Deep Learning in Photoacoustic Tomography: Current Approaches and Future Directions. J. Biomed. Opt. 2020, 25, 112903. [Google Scholar] [CrossRef]
- Gröhl, J.; Schellenberg, M.; Dreher, K.; Maier-Hein, L. Deep Learning for Biomedical Photoacoustic Imaging: A Review. Photoacoustics 2021, 22, 100241. [Google Scholar] [CrossRef]
- Yang, C.; Lan, H.; Gao, F.; Gao, F. Review of Deep Learning for Photoacoustic Imaging. Photoacoustics 2021, 21, 100215. [Google Scholar] [CrossRef]
- Deng, H.; Qiao, H.; Dai, Q.; Ma, C. Deep Learning in Photoacoustic Imaging: A Review. J. Biomed. Opt. 2021, 26, 040901. [Google Scholar] [CrossRef]
- Rajendran, P.; Sharma, A.; Pramanik, M. Photoacoustic Imaging Aided with Deep Learning: A Review. Biomed. Eng. Lett. 2022, 12, 155–173. [Google Scholar] [CrossRef]
- Stylogiannis, A.; Kousias, N.; Kontses, A.; Ntziachristos, L.; Ntziachristos, V. A Low-Cost Optoacoustic Sensor for Environmental Monitoring. Sensors 2021, 21, 1379. [Google Scholar] [CrossRef]
- Shorman, S.M.; Pitchay, S.A. A Review of Rain Streaks Detection and Removal Techniques for Outdoor Single Image. ARPN J. Eng. Appl. Sci. 2016, 11, 6303–6308. [Google Scholar]
- Wang, H.; Wu, Y.; Li, M.; Zhao, Q.; Meng, D. Survey on Rain Removal from Videos or a Single Image. Sci. China Inf. Sci. 2022, 65, 111101. [Google Scholar] [CrossRef]
- Shi, Z.; Li, Y.; Zhang, C.; Zhao, M.; Feng, Y.; Jiang, B. Weighted Median Guided Filtering Method for Single Image Rain Removal. Eurasip J. Image Video Process. 2018, 2018, 35. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Rivenson, Y.; Jin, Y.; Wei, Z.; Gao, R.; Günaydın, H.; Bentolila, L.A.; Kural, C.; Ozcan, A. Deep Learning Enables Cross-Modality Super-Resolution in Fluorescence Microscopy. Nat. Methods 2019, 16, 103–110. [Google Scholar] [CrossRef]
- Liu, T.; de Haan, K.; Rivenson, Y.; Wei, Z.; Zeng, X.; Zhang, Y.; Ozcan, A. Learning-Based Super-Resolution in Coherent Imaging Systems. Sci. Rep. 2019, 9, 3926. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.S.; Tyring, A.J.; Deruyter, N.P.; Wu, Y.; Rokem, A.; Lee, A.Y. Deep-Learning Based, Automated Segmentation of Macular Edema in Optical Coherence Tomography. Biomed. Opt. Express 2017, 8, 3440–3448. [Google Scholar] [CrossRef] [Green Version]
- Yuan, A.Y.; Gao, Y.; Peng, L.; Zhou, L.; Liu, J.; Zhu, S.; Song, W. Hybrid Deep Learning Network for Vascular Segmentation in Photoacoustic Imaging. Biomed. Opt. Express 2020, 11, 6445–6457. [Google Scholar] [CrossRef]
- Devalla, S.K.; Subramanian, G.; Pham, T.H.; Wang, X.; Perera, S.; Tun, T.A.; Aung, T.; Schmetterer, L.; Thiéry, A.H.; Girard, M.J.A. A Deep Learning Approach to Denoise Optical Coherence Tomography Images of the Optic Nerve Head. Sci. Rep. 2019, 9, 14454. [Google Scholar] [CrossRef] [PubMed]
- Qiu, B.; Huang, Z.; Liu, X.; Meng, X.; You, Y.; Liu, G.; Yang, K.; Maier, A.; Ren, Q.; Lu, Y. Noise Reduction in Optical Coherence Tomography Images Using a Deep Neural Network with Perceptually-Sensitive Loss Function. Biomed. Opt. Express 2020, 11, 817–830. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Vinod, N.; Geoffrey, H. Rectified Linear Units Improve Restricted Boltzmann Machines Vinod Nair. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; Volume 27, pp. 807–814. [Google Scholar]
- Nagi, J.; Ducatelle, F.; Di Caro, G.A.; Ciresan, D.; Meier, U.; Giusti, A.; Nagi, F.; Schmidhuber, J.; Gambardella, L.M. Max-Pooling Convolutional Neural Networks for Vision-Based Hand Gesture Recognition. In Proceedings of the 2011 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuala Lumpur, Malaysia, 16–18 November 2011; pp. 342–347. [Google Scholar]
- Lee, S.; Lee, C. Revisiting Spatial Dropout for Regularizing Convolutional Neural Networks. Multimed. Tools Appl. 2020, 79, 34195–34207. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37. [Google Scholar]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Brochu, E.; Cora, V.M.; de Freitas, N. A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. arXiv 2010, arXiv:1012.2599. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.; Deng, S.; Gueguen, L.; Wei, M.; Wu, X.; Qin, J. Convolutional Neural Network with Median Layers for Denoising Salt-And-Pepper Contaminations. Neurocomputing 2021, 442, 26–35. [Google Scholar] [CrossRef]
- Agrawal, S.; Fadden, C.; Dangi, A.; Yang, X.; Albahrani, H.; Frings, N.; Heidari Zadi, S.; Kothapalli, S.-R. Light-Emitting-Diode-Based Multispectral Photoacoustic Computed Tomography System. Sensors 2019, 19, 4861. [Google Scholar] [CrossRef] [Green Version]
- Francis, K.J.; Booijink, R.; Bansal, R.; Steenbergen, W. Tomographic Ultrasound and LED-Based Photoacoustic System for Preclinical Imaging. Sensors 2020, 20, 2793. [Google Scholar] [CrossRef]
- Bulsink, R.; Kuniyil Ajith Singh, M.; Xavierselvan, M.; Mallidi, S.; Steenbergen, W.; Francis, K.J. Oxygen Saturation Imaging Using LED-Based Photoacoustic System. Sensors 2021, 21, 283. [Google Scholar] [CrossRef]






| Initial Learning Rate | Epoch Number | L2 Regularization | Training RMSE | |
|---|---|---|---|---|
| U-Net | 0.0002 | 70 | 0.0465 | 33.2993 |
| Segnet | 0.0010 | 93 | 0.0497 | 1028.6909 |
| FCN-16s | 0.0003 | 84 | 0.0166 | 291.4638 |
| FCN-8s | 0.0002 | 78 | 0.0205 | 344.4395 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulenko, O.; Yang, H.; Kim, K.; Youm, J.Y.; Kim, M.; Kim, Y.; Jung, W.; Yang, J.-M. Deep-Learning-Based Algorithm for the Removal of Electromagnetic Interference Noise in Photoacoustic Endoscopic Image Processing. Sensors 2022, 22, 3961. https://doi.org/10.3390/s22103961
Gulenko O, Yang H, Kim K, Youm JY, Kim M, Kim Y, Jung W, Yang J-M. Deep-Learning-Based Algorithm for the Removal of Electromagnetic Interference Noise in Photoacoustic Endoscopic Image Processing. Sensors. 2022; 22(10):3961. https://doi.org/10.3390/s22103961
Chicago/Turabian StyleGulenko, Oleksandra, Hyunmo Yang, KiSik Kim, Jin Young Youm, Minjae Kim, Yunho Kim, Woonggyu Jung, and Joon-Mo Yang. 2022. "Deep-Learning-Based Algorithm for the Removal of Electromagnetic Interference Noise in Photoacoustic Endoscopic Image Processing" Sensors 22, no. 10: 3961. https://doi.org/10.3390/s22103961
APA StyleGulenko, O., Yang, H., Kim, K., Youm, J. Y., Kim, M., Kim, Y., Jung, W., & Yang, J. -M. (2022). Deep-Learning-Based Algorithm for the Removal of Electromagnetic Interference Noise in Photoacoustic Endoscopic Image Processing. Sensors, 22(10), 3961. https://doi.org/10.3390/s22103961