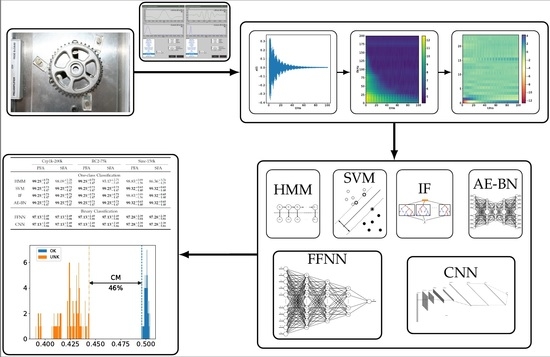
1. Introduction
Since the industrial age cogwheels (the term cogwheels may be considered as gears but not gearboxes or bearing systems) have been indispensable components in manufacturing, e.g., the textile and automotive industries, and they still play a significant role even in this information age, e.g., robotics and aerospace. This makes developing reliable and cost-effective non-destructive testing (NDT) methods an integral part of quality control (QC).
The field involved with cogwheels is vast, and yet most work in the literature has been performed in the context of gearboxes or bearing systems [
1,
2,
3,
4,
5,
6,
7], i.e., many gears are inside in a system and attached to each other. For such systems, the main focus of fault detection lies on a system failure dealing with conditions monitoring in lifespan analysis, which occurs mainly due to malfunctioning components suffering from wear, abrasion and pollution, such as sand or lubrication.
However, this necessarily leads to different directions of research, when the structural health diagnosis of cogwheels in manufacturing process, e.g., sintering, comes into focus. Moreover, this often encounters small data problems simply due to lacking data of defective parts; see, e.g., [
4]. Here, small data problems refer specifically to the situation when there are not enough data available for training algorithms in machine learning (ML), which poses difficulties in various fields as, e.g., can be seen in [
8].
Although gearboxes or bearing systems related work have made progress [
5,
6,
7], usually by means of modern deep learning (DL) [
9], the employed methods are
not always applicable to small data problems as discussed in [
10,
11], e.g., 22 layers of GoogLeNet [
12] used in [
6].
Moreover, not all studies reflect real-world scenarios, e.g., the tooth of a gear is intentionally cut off [
5]. In addition, many studies do
not mention the sample size of a dataset
nor countermeasures against overfitting whether the proposed work is suitable for small data problems, e.g., [
7]. Additionally, ML methods employed in some work dealing with small data are still limited to shallow learning [
3], i.e., traditional ML [
10]. In order to show missing points in the field and different aspects of this study, we provide an overview of signal-based methods in
Table 1.
When it comes to NDT, other than signal-based approaches, there also exist image-based methods and they have made considerable progress since modern DL-based algorithms have become part of the mainstream across most research disciplines [
13,
14] due mainly to the work by Krizhevsky et al. [
15]. However, in this study, we focus solely on signal-based methods on the grounds that image-based approaches are not as cost-effective as signal-based ones [
16], and the methods become futile when defects in images are invisible as in our case. In addition, among different ML algorithms, we call them modern when the employed approaches are involved with DL-based ones; otherwise, we call them classical.
Hence, given a summary about the matter in
Table 1, apart from gearboxes or bearing systems, to the best of our knowledge, there has actually been
no extensive study on sintered cogwheel small data using acoustic resonance testing (ART) [
17] with the help of traditional and modern ML methods in the context of non-destructive testing (NDT).
Our Contributions: In this work, we address the aforementioned issues and intend to bridge the gap: We collect a small dataset on cogwheels and perform time-frequency domain feature analysis.
Afterwards, we apply not only classical ML algorithms but also modern DL-based ones to the obtained feature sets in the way of one-class as well as binary classification. In this way, in spite of having small data, our approach is able to achieve robust performance: All defective test samples reflecting real-world scenarios are recognized in two one-class classifiers (also called detectors) and one intact test sample is misclassified in binary classification. This suggests that ART can be an attractive tool on cogwheel data in QC when taking advantage of the combination of ML algorithms and time-frequency domain feature analysis.
Paper Organization: The paper is organized as follows: After we give a brief exposition on data acquisition and feature analysis in
Section 2, we provide information on training of ML algorithms in
Section 3. Then, we present the result of experiments in
Section 4. Finally, the paper is closed with our concluding remarks.
3. Training of Classifiers
Given the dataset, the main goal of our experiment is to investigate which combination of ML methods and feature sets are appropriate for recognizing real-world defects. To this end, we first considered one-class-based methods as applied in anomaly detection in order to deal with the limitations in sample size and imbalance of the acquired dataset:
hidden Markov model (HMM),
support-vector machine (SVM),
isolation forest (IF), and
autoencoder of bottleneck type (AE-BN).
Moreover, we also applied the following methods in the way of binary classification:
Although NN-based methods, such as CNNs, are well-known to be useful for constructing feature maps from raw signals [
9], this comes at the expensive price of a large dataset for training [
21]. Moreover, this is often
not a viable option as in our situation.
On this account, we restrict ourselves to PFA and SFA feature sets for training.
3.1. Configuration of Experiments
The dataset is prepared in a way that there is no overlap between training and test sets. Stratified five-fold cross validation (CV) is employed during all experiments to ensure good representation of the whole classes in the training and test folds. For one-class classification, this strategy is realized in such a way that training is performed only on intact samples without a designated fold and tested against all damaged ones with the reserved fold as illustrated in
Figure 4. The reasoning behind this is to circumvent overfitting as much as possible by exploiting the common properties of small dataset, i.e., few damaged samples compared to intact ones.
3.1.1. Hidden Markov Models
HMMs can be viewed as an extension of a mixture model, where the choice of the mixture component for each observation is not selected independently but depends on the choice of component for the previous observation. This is called the Markov property [
22]. Since HMMs are useful for dealing with sequential data, they are widely used in speech recognition [
23] and natural language processing [
24].
However, they have also been successfully applied in advanced NDT [
25]. Although long short-term memory (LSTM) is known to be good at dealing with variable length of sequential data [
26], we instead make use of a simpler model HMM considering that our feature sets PFA and SFA have fixed dimensions. Our HMM is designed in such a way that ten hidden states release observations that correspond to our acquired dataset via one Gaussian probability density function with a full covariance matrix in each state. To detect anomalies, we used the interquartile range by measuring a score characterizing how well our model describes an observation point. The experiments are conducted by means of the dLabPro package [
27], and the model parameters are estimated by the Baum–Welch algorithm [
28].
3.1.2. Support-Vector Machines
The SVM is a generalization of the maximal margin classifier, and it classifies data points by constructing a separating hyperplane that distinguishes one class from others [
29]. SVMs are extremely powerful ML algorithms to solve various classification problems in that not only are they less prone to overfitting due to large margins but they are also relatively manageable to solve due to convex nature. Moreover, it is also well-known that they are effective in dealing with high dimensions of features—particularly when the number of features are much more than training samples—by making use of kernel tricks regarding nonlinear classification problems.
Our experiments were implemented using the scikit-learn [
30] interface relying on the LIBSVM library [
31]. SVM models were trained using the radial basis function (RBF) kernel, and the following parameters were tuned on about 20% of the training set to obtain optimal results: (1) regularization parameter C (from
to
), and (2)
, which defines how far a single sample influences (from
to
), or (3)
, which has the ability to control over the number of support vectors (from
to 1), if necessary.
3.1.3. Isolation Forest
Isolation forest belongs to the family of ensemble methods and is a tree-based anomaly detection algorithm that isolates observations as outliers based on the anomaly score delivered by profiling a randomly selected feature with a random split value between minimum and maximum values of the selected feature [
32,
33]. This has been a useful technique in wide range of fields, e.g., finding anomalies in hyperspectral remote sensing images [
34], detecting anomalous taxi trajectories from GPS traces [
35], or in analyzing partial discharge signals of a power equipment [
36].
Our experiments are realized by scikit-learn [
30]: the minimum split number is set to 2, and the maximum depth of each tree is defined by
, where
n denotes the number of samples used to build the tree.
3.1.4. Autoencoder of Bottleneck Type
An autoencoder refers to a type of ANN which aims at approximating original input signal in an unsupervised way [
37], which is composed of two parts: encoding and decoding layers. The encoding layers are responsible for finding an efficient representation of the input vectors by learning useful features, and decoding layers attempt to reconstruct the input signal as close as possible from the acquired encoded information. Since AEs are capable of generating the compact representation of input data, which is extremely useful in terms of feature learning, there is an enormous potential to solve various problems, such as anomaly detection [
38], image denoising [
39] and shape recognition [
40].
Our experiments were performed by leveraging Keras [
41] with TensorFlow [
42] and the following feed-forward bottleneck type architecture is employed: input-512-64-512-output. As shown in
Figure 5, the input and output size are equal to the dimensions of the vectorized feature sets, i.e., 19,560 for PFA and 15,648 for SFA, respectively.
All layers are fully connected and activated by leaky rectified linear unit (LReLU) to overcome vanishing gradient [
43]. In addition, to deal with internal covariant shift
batch normalization (BNorm) is applied to each layer [
44].
Moreover, as countermeasures against overfitting, which, in our case, is of grave concern particularly due to small data, random
dropout with a 0.5 rate in internal layers [
45] and the
early stopping strategy making use of the
patience parameter with 25 are considered [
46], where the patience specifies the number of epochs with no improvement in terms of the used loss function, after which, training will be halted [
41]. Given the maximum number of epochs to be 500 in our experiments, the early stopping criterion comes into play in a range from epochs 132 to 445 depending on the folds in the datasets.
Our AE-BNs have about 20 million parameters, and for training, adaptive moment estimation (Adam) optimization [
47] is incorporated along with
regularization to obtain sparse solutions. Hyperparameter optimization using grid search is conducted on about 20% of training set in pre-training stages to obtain suitable parameter values, such as training batch size 512 and the aforementioned dropout rate 0.5.
3.1.5. Deep Learning for Binary Classification
DL may be defined as a class of ML algorithms that typically make use of multilayer NNs in order to progressively extract different levels of representations of input data, which correspond to a hierarchy of features [
48]. While the input data are being processed in multiple layers, each layer allows to reveal additional features of the input in such a way that higher level features are described in terms of lower level ones to help understand the data. As in [
49], this can be understood in the following example from image classification:
Given an image of a dog as input, for instance, pixel values are detected in the first layer; edges are identified in the second layer; combinations of edges and other complex features based on the edges from the previous layer are identified in next several layers; and finally the input image is recognized as a dog in output.
Apart from the different levels of abstraction, due to the capability of nonlinear information processing, DL-based approaches have recently become popular in many fields, including, but not limited to, image processing, computer vision, speech recognition, and natural language processing [
50]. As in the case of AE-BN, our DL routines were also realized by Keras [
41] using TensorFlow [
42], and the following architectures were employed: Three hidden layers are stacked and fully connected, see
Figure 6. These hidden layers are incorporated with 600, 300 and 100 nodes and activated by the LReLU function. In addition, BNorm and a dropout rate of 0.5 are employed in each layer. Other configurations are similar to those of AE-BE: The Adam optimizer along with
regularization, early stopping by means of the patience parameter with 25, batch size with 256 and maximum number of epochs with 200 are considered. From one node in the output layer, binary classification is realized using binary cross-entropy loss by mapping “UNK” to 0 and “OK” to 1. Our FFNN has about 12 million parameters.
In the case of CNN, three 2-D convolution layers with the kernel size of are employed, each of which has 16, 32 and 64 feature maps and is downsampled with the stride of . Then, the LReLU activation function, BNorm and dropout rate with 0.75 and a 2-D max pooling layer with , which is another way to deal with overfitting, are applied to each layer. Then, the result is flattened and fed into a fully connected layer with 50 nodes activated by LReLU, where BNorm and the dropout rate 0.75 are also used.
As can be noticed, a relative high dropout rate is chosen for reducing model complexity in the light of overfitting owing to the small size of defective samples. Compared to the case of FFNN, other configurations for training remain unchanged except the maximum number of epochs at 300. The architecture of CNN is provided in
Table 4. Binary classification is implemented in the same way as in the case of FFNN. Our CNN has approximately sixty thousand parameters.