Development of an Online Adaptive Parameter Tuning vSLAM Algorithm for UAVs in GPS-Denied Environments
Abstract
:1. Introduction
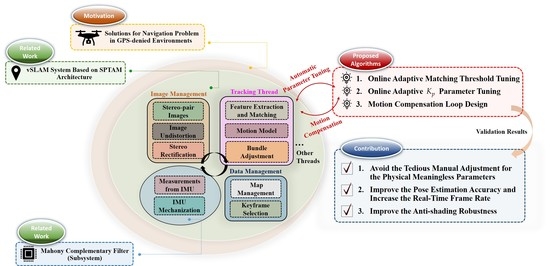
- Online adaptive parameter tuning for feature matching threshold, which lacks physical meaning.
- Online adaptive gain adjustment for Mahony complementary filter to resist aggressive motions.
- Fusion and motion compensation loop design between vSLAM and IMU.
- The matching threshold and the gain, which are not easy to determine via manual tuning, are adjusted adaptively according to the UAVs’ flight status.
- The proposed online adaptive parameter tuning algorithm can effectively improve the pose estimation accuracy and can enhance frame per second (FPS) by up to 70% and 29%, respectively, in the EuRoC dataset.
- The developed motion compensation loop subroutine can effectively utilize IMU information to improve the anti-shading robustness of the original vSLAM performance. Moreover, incorporating the presented online adaptive parameter tuning algorithm can further improve the robustness to a higher level.
2. The Framework of the vSLAM System
2.1. Coordinate Setup
2.2. Keyframe Selection
2.3. Tracking Thread
- The output of the constant velocity motion model may be a weak initial guess, especially when UAVs are in aggressive motions such as sharp turnings or lost image information.
- The optimization of the BA is highly dependent on the accuracy of feature matching.
2.4. Feature Extraction and Matching
2.5. Bundle Adjustment
3. Online Adaptive Matching Threshold Tuning for vSLAM System
3.1. Accuracy Analysis under Different Matching Thresholds
3.2. Online Adaptive Matching Threshold Tuning Algorithm
4. Online Adaptive Parameter Tuning for Mahony Complementary Filter
4.1. Mahony Complementary Filter
4.2. Online Adaptive Tuning
- Pure Integration (control group):
- Arctan Method (control group):
- Pure Mahony (control group):
- Conditional Method (experimental group):
- Adaptive Method Version. 1 (experimental group):
- Adaptive Method Version. 2 (experimental group):
- Adaptive Method Version. 3 (experimental group):
5. Motion Compensation Loop Design
5.1. Static State Detection Algorithm
5.2. Motion Compensation Proccess
6. Experiment Verification
6.1. Ablation Studied for Accuracy Comparison
- Case. 1: not to use both proposed online adaptive tuning algorithms.
- Case. 2: only use the online adaptive matching threshold tuning algorithm.
- Case. 3: only use the online adaptive tuning algorithm.
- Case. 4: use both proposed online adaptive tuning algorithms.
6.2. Anti-Shading Robustness Test
- Case. A: without using both the online adaptive parameter tuning algorithm and the motion compensation loop subroutine.
- Case. B: only using motion compensation loop subroutine.
- Case. C: using the proposed online adaptive parameter tuning algorithm and the motion compensation loop subroutine.
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khosiawan, Y.; Park, Y.; Moon, I.; Nilakantan, J.M.; Nielsen, I. Task scheduling system for UAV operations in indoor environment. Neural Comput. Appl. 2019, 31, 5431–5459. [Google Scholar] [CrossRef] [Green Version]
- Khosiawan, Y.; Nielsen, I. A system of UAV application in indoor environment. Prod. Manuf. Res. 2016, 4, 2–22. [Google Scholar] [CrossRef] [Green Version]
- Kaneko, M.; Iwami, K.; Ogawa, T.; Yamasaki, T.; Aizawa, K. Mask-slam: Robust feature-based monocular slam by masking using semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 258–266. [Google Scholar]
- Wang, Y.; Zell, A. Improving Feature-based Visual SLAM by Semantics. In Proceedings of the 2018 IEEE International Conference on Image Processing, Applications and Systems (IPAS), Genova, Italy, 12–14 December 2018; pp. 7–12. [Google Scholar]
- Yu, C.; Liu, Z.; Liu, X.J.; Xie, F.; Yang, Y.; Wei, Q.; Fei, Q. DS-SLAM: A Semantic Visual SLAM towards Dynamic Environments. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1168–1174. [Google Scholar]
- Truong, P.H.; You, S.; Ji, S. Object Detection-based Semantic Map Building for A Semantic Visual SLAM System. In Proceedings of the 2020 20th International Conference on Control, Automation and Systems (ICCAS), Busan, Korea, 13–16 October 2020; pp. 1198–1201. [Google Scholar]
- Klein, G.; Murray, D. Parallel Tracking and Mapping for Small AR Workspaces. In Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, Washington, DC, USA, 13–16 November 2007; pp. 225–234. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef] [Green Version]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Andert, F.; Mejias, L. Improving monocular SLAM with altimeter hints for fixed-wing aircraft navigation and emergency landing. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 1008–1016. [Google Scholar]
- Yang, T.; Li, P.; Zhang, H.; Li, J.; Li, Z. Monocular Vision SLAM-Based UAV Autonomous Landing in Emergencies and Unknown Environments. Electronics 2018, 7, 73. [Google Scholar] [CrossRef] [Green Version]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef] [Green Version]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar]
- Whelan, T.; Salas-Moreno, R.F.; Glocker, B.; Davison, A.J.; Leutenegger, S. ElasticFusion: Real-time dense SLAM and light source estimation. Int. J. Robot. Res. 2016, 35, 1697–1716. [Google Scholar] [CrossRef] [Green Version]
- Kerl, C.; Sturm, J.; Cremers, D. Dense visual SLAM for RGB-D cameras. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2100–2106. [Google Scholar]
- Endres, F.; Hess, J.; Sturm, J.; Cremers, D.; Burgard, W. 3-D Mapping With an RGB-D Camera. IEEE Trans. Robot. 2014, 30, 177–187. [Google Scholar] [CrossRef]
- Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J.; Kohi, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A. KinectFusion: Real-time dense surface mapping and tracking. In Proceedings of the 2011 10th IEEE International Symposium on Mixed and Augmented Reality, Singapore, 26–29 October 2011; pp. 127–136. [Google Scholar]
- Sun, K.; Mohta, K.; Pfrommer, B.; Watterson, M.; Liu, S.; Mulgaonkar, Y.; Taylor, C.J.; Kumar, V. Robust Stereo Visual Inertial Odometry for Fast Autonomous Flight. IEEE Robot. Autom. Lett. 2018, 3, 965–972. [Google Scholar] [CrossRef]
- Pire, T.; Fischer, T.; Castro, G.; De Cristóforis, P.; Civera, J.; Jacobo Berlles, J. S-PTAM: Stereo Parallel Tracking and Mapping. Robot. Auton. Syst. 2017, 93, 27–42. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Zhu, L.; Lin, X.; Guan, Y.; He, L.; Zhang, H. Dynamic Strategy of Keyframe Selection with PD Controller for VSLAM Systems. IEEE/ASME Trans. Mechatron. 2021, 27, 115–125. [Google Scholar] [CrossRef]
- Euston, M.; Coote, P.; Mahony, R.; Kim, J.; Hamel, T. A complementary filter for attitude estimation of a fixed-wing UAV. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 340–345. [Google Scholar]
- Uoip. Stereo_Ptam. Available online: https://github.com/uoip/stereo_ptam (accessed on 20 August 2022).
- Engel, J.; Stückler, J.; Cremers, D. Large-scale direct SLAM with stereo cameras. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1935–1942. [Google Scholar]
- Burri, M.; Nikolic, J.; Gohl, P.; Schneider, T.; Rehder, J.; Omari, S.; Achtelik, M.W.; Siegwart, R. The EuRoC micro aerial vehicle datasets. Int. J. Robot. Res. 2016, 35, 1157–1163. [Google Scholar] [CrossRef]
- Jianbo, S.; Tomasi. Good features to track. In Proceedings of the 1994 Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features. In Proceedings of the Computer Vision—ECCV 2010, Berlin, Heidelberg, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Gao, X.; Zhang, T.; Liu, Y.; Yan, Q. 14 Lectures on Visual SLAM: From Theory to Practice; Publishing House of Electronics Industry: Beijing, China, 2017. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]


























| Series | Error Type | |||
|---|---|---|---|---|
| MH_01_easy | RPE | 0.483251 | 0.503435 | 0.404268 |
| ATE | 0.578836 | 0.615321 | 0.503354 |
| Parameter | Setting Value |
|---|---|
| 0.65 | |
| 5 | |
| 1 | |
| 6 | |
| 45 | |
| 5 |
| Parameter | Setting Value |
|---|---|
| 0.01 | |
| 0.15 | |
| 12 | |
| * | 0.4 |
| Method\Series | MH_01_Easy | MH_02_Easy | MH_03_Medium | MH_04_Difficult | MH_05_Difficult | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Roll (RMSE) | Pitch (RMSE) | Roll (RMSE) | Pitch (RMSE) | Roll (RMSE) | Pitch (RMSE) | Roll (RMSE) | Pitch (RMSE) | Roll (RMSE) | Pitch (RMSE) | |
| Pure Integration | 1.2140 | 0.8997 | 0.3969 | 0.3090 | 0.1739 | 0.2019 | 0.28612 | 0.2080 | 0.32292 | 0.2605 |
| Arctan Method | 2.0094 | 1.7620 | 1.5191 | 1.6333 | 4.3881 | 3.9834 | 2.4454 | 2.6123 | 2.4323 | 2.4165 |
| Pure Mahony | 0.35373 | 0.2963 | 0.2513 | 0.3500 | 0.88704 | 0.6433 | 0.72719 | 0.5796 | 0.6052 | 0.5560 |
| Conditional Method | 1.1734 | 0.5215 | 0.3013 | 0.2087 | 0.1246 | 0.1592 | 0.2944 | 0.1838 | 0.2704 | 0.2456 |
| Adaptive Method Version.1 | 1.1634 | 0.5930 | 0.3226 | 0.2182 | 0.1272 | 0.1651 | 0.2949 | 0.1899 | 0.2847 | 0.2471 |
| Adaptive Method Version. 2 | 1.1724 | 0.5270 | 0.30324 | 0.2091 | 0.12412 | 0.1595 | 0.2946 | 0.1845 | 0.2718 | 0.2457 |
| Adaptive Method Version. 3 | 1.0487 | 0.4166 | 0.29874 | 0.2084 | 0.12569 | 0.1590 | 0.2928 | 0.1802 | 0.2216 | 0.2448 |
| Series | Time Stamp (Second) for Triggering Static State Detection Algorithm (Checked from Figure 15) | The True State of The UAV is Stationary or Not (Checked from Images) | Angle Error (deg) * | ||
|---|---|---|---|---|---|
| MH_01_easy | 23.5 | yes | 4.0044 | −0.008034 | |
| 15.6614 | −0.034309 | ||||
| MH_02_easy | 28.75 | yes | 3.3513 | 0.001947 | |
| 15.5490 | −0.047756 | ||||
| MH_03_medium | 11.25 | yes | 4.8658 | 0.050396 | |
| 15.6173 | −0.045054 | ||||
| MH_04_difficult | 13 | yes | 0.4097 | −0.073378 | |
| 24.1770 | 0.113550 | ||||
| MH_05_ difficult | 14.75 | yes | 0.1934 | −0.006640 | |
| 23.9930 | 0.095132 | ||||
| CPU | RAM |
|---|---|
| Intel Core i7-11800H @2.30GHz | 16 GB |
| Scenarios | Series | Time Stamp (Second) for Image Loss | RPE (Meter) | ATE (Meter) |
|---|---|---|---|---|
| Case. A (Pure vSLAM) | MH_01_easy | 55.45~56.95 | Tracking Fail | Tracking Fail |
| MH_02_easy | 55.45~57.95 | Tracking Fail | Tracking Fail | |
| MH_03_medium | 42.35~44.35 | Tracking Fail | Tracking Fail | |
| MH_04_difficult | 34.95~36.45 | Tracking Fail | Tracking Fail | |
| MH_05_ difficult | 74.95~77.45 | Tracking Fail | Tracking Fail | |
| Case. B (vSALM with the proposed motion compensation loop) | MH_01_easy | 55.45~56.95 | 0.5200 | 0.6119 |
| MH_02_easy | 55.45~57.95 | 0.4210 | 0.5292 | |
| MH_03_medium | 42.35~44.35 | Tracking Fail | Tracking Fail | |
| MH_04_difficult | 34.95~36.45 | Tracking Fail | Tracking Fail | |
| MH_05_ difficult | 74.95~77.45 | 1.1378 | 0.8813 | |
| Case. C (vSALM with the proposed online adaptive parameter tuning and motion compensation loop) | MH_01_easy | 55.45~56.95 | 0.2578 | 0.3290 |
| MH_02_easy | 55.45~57.95 | 0.3686 | 0.4471 | |
| MH_03_medium | 42.35~44.35 | 0.4248 | 0.4615 | |
| MH_04_difficult | 34.95~36.45 | 0.7099 | 0.7794 | |
| MH_05_ difficult | 74.95~77.45 | 1.0806 | 0.8940 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-L.; He, R.; Peng, C.-C. Development of an Online Adaptive Parameter Tuning vSLAM Algorithm for UAVs in GPS-Denied Environments. Sensors 2022, 22, 8067. https://doi.org/10.3390/s22208067
Chen C-L, He R, Peng C-C. Development of an Online Adaptive Parameter Tuning vSLAM Algorithm for UAVs in GPS-Denied Environments. Sensors. 2022; 22(20):8067. https://doi.org/10.3390/s22208067
Chicago/Turabian StyleChen, Chieh-Li, Rong He, and Chao-Chung Peng. 2022. "Development of an Online Adaptive Parameter Tuning vSLAM Algorithm for UAVs in GPS-Denied Environments" Sensors 22, no. 20: 8067. https://doi.org/10.3390/s22208067
APA StyleChen, C. -L., He, R., & Peng, C. -C. (2022). Development of an Online Adaptive Parameter Tuning vSLAM Algorithm for UAVs in GPS-Denied Environments. Sensors, 22(20), 8067. https://doi.org/10.3390/s22208067