Online Condition Monitoring of Rotating Machines by Self-Powered Piezoelectric Transducer from Real-Time Experimental Investigations
Abstract
:1. Introduction
2. Methodology
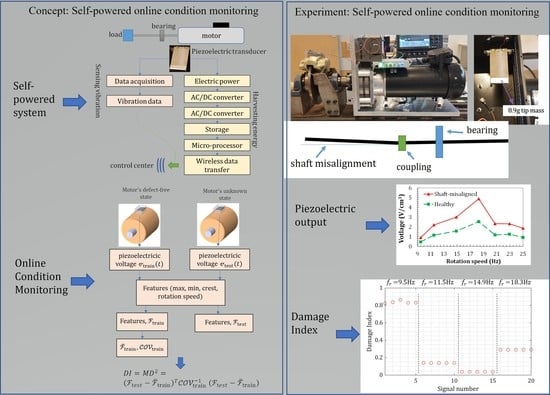
2.1. Online Condition Monitoring (OCM) by the Self-Powered Sensor
2.2. Energy Harvesting System and Piezoelectric Generator Modeling
3. Experimental Setup for Measurement
4. Piezoelectric Generator Model Verification
5. Results and Discussions
5.1. Energy Harvesting from the Motor’s Main Bearing
5.2. Toward a Self-Powered Online Condition Monitoring System
5.3. Fault Effects on the Piezoelectric Transducer as a Sensor
5.4. Fault Detection
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khazaee, M.; Ahmadi, H.; Omid, M.; Moosavian, A.; Khazaee, M. Classifier Fusion of Vibration and Acoustic Signals for Fault Diagnosis and Classification of Planetary Gears Based on Dempster-Shafer Evidence Theory. Proc. Inst. Mech. Eng. Part E-J. Process Mech. Eng. 2014, 228, 21–32. [Google Scholar] [CrossRef]
- Delgado-Arredondo, P.A.; Morinigo-Sotelo, D.; Osornio-Rios, R.A.; Avina-Cervantes, J.G.; Rostro-Gonzalez, H.; de Jesus Romero-Troncoso, R. Methodology for Fault Detection in Induction Motors via Sound and Vibration Signals. Mech. Syst. Signal Process. 2017, 83, 568–589. [Google Scholar] [CrossRef]
- Ribeiro Junior, R.F.; dos Santos Areias, I.A.; Gomes, G.F. Fault Detection and Diagnosis Using Vibration Signal Analysis in Frequency Domain for Electric Motors Considering Different Real Fault Types. Sens. Rev. 2021, 41, 311–319. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Signal Based Condition Monitoring Techniques for Fault Detection and Diagnosis of Induction Motors: A State-of-the-Art Review. Mech. Syst. Signal Process. 2020, 144, 106908. [Google Scholar] [CrossRef]
- Ugwiri, M.A.; Carratu, M.; Pietrosanto, A.; Paciello, V.; Lay-Ekuakille, A. Vibrations Measurement and Current Signatures for Fault Detection in Asynchronous Motor. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 20–25. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Multifault Diagnosis of Induction Motor at Intermediate Operating Conditions Using Wavelet Packet Transform and Support Vector Machine. J. Dyn. Syst. Meas. Control. Trans. ASME 2018, 140, 081014. [Google Scholar] [CrossRef]
- Kudelina, K.; Vaimann, T.; Rassolkin, A.; Kallaste, A. Impact of Bearing Faults on Vibration Level of BLDC Motor. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021. [Google Scholar] [CrossRef]
- Ulriksen, M.D.; Tcherniak, D.; Hansen, L.M.; Johansen, R.J.; Damkilde, L.; Frøyd, L. In-Situ Damage Localization for a Wind Turbine Blade through Outlier Analysis of Stochastic Dynamic Damage Location Vector-Induced Stress Resultants. Struct. Health Monit. 2017, 16, 745–761. [Google Scholar] [CrossRef]
- Ulriksen, M.D.; Tcherniak, D.; Damkilde, L. Damage Detection in an Operating Vestas V27 Wind Turbine Blade by Use of Outlier Analysis. In Proceedings of the 2015 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS) Proceedings, Trento, Italy, 9–10 July 2015; pp. 50–55. [Google Scholar] [CrossRef]
- Khaligh, A.; Zeng, P.; Zheng, C. Kinetic Energy Harvesting Using Piezoelectric and Electromagnetic Technologies; State of the Art. Ind. Electron. IEEE Trans. 2010, 57, 850–860. [Google Scholar] [CrossRef]
- Ahmed, R.; Mir, F.; Banerjee, S. A Review on Energy Harvesting Approaches for Renewable Energies from Ambient Vibrations and Acoustic Waves Using Piezoelectricity. Smart Mater. Struct. 2017, 26, 085031. [Google Scholar] [CrossRef]
- Neuzil, J.; Kreibich, O.; Smid, R. A Distributed Fault Detection System Based on IWSN for Machine Condition Monitoring. IEEE Trans. Ind. Inform. 2014, 10, 1118–1123. [Google Scholar] [CrossRef]
- Cao, S.; Li, J. A Survey on Ambient Energy Sources and Harvesting Methods for Structural Health Monitoring Applications. Adv. Mech. Eng. 2017, 9, 168781401769621. [Google Scholar] [CrossRef]
- De Marqui, C.; Erturk, A. Electroaeroelastic Analysis of Airfoil-Based Wind Energy Harvesting Using Piezoelectric Transduction and Electromagnetic Induction. J. Intell. Mater. Syst. Struct. 2013, 24, 846–854. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Deng, Z.D. Energy Harvesting from Low Frequency Applications Using Piezoelectric Materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef] [Green Version]
- Khazaee, M.; Rezaniakolaei, A.; Rosendahl, L. An Experimental Study on Macro Piezoceramic Fiber Composites for Energy Harvesting. Mater. Sci. Forum 2019, 951, 3–8. [Google Scholar] [CrossRef]
- Cahill, P.; Hazra, B.; Karoumi, R.; Mathewson, A.; Pakrashi, V. Vibration Energy Harvesting Based Monitoring of an Operational Bridge Undegoing Forced Vibration and Train Passage. Mech. Syst. Signal Process. 2018, 106, 265–283. [Google Scholar] [CrossRef] [Green Version]
- Khazaee, M.; Rezaniakolaie, A.; Moosavian, A.; Rosendahl, L. A Novel Method for Autonomous Remote Condition Monitoring of Rotating Machines Using Piezoelectric Energy Harvesting Approach. Sens. Actuators A Phys. 2019, 295, 37–50. [Google Scholar] [CrossRef]
- Lim, D.-W.; Mantell, S.C.; Seiler, P.J. Wireless Monitoring Algorithm for Wind Turbine Blades Using Piezo-Electric Energy Harvesters. Wind Energy 2017, 20, 551–565. [Google Scholar] [CrossRef]
- Zhanga, Z.; Nib, C.; Zhangc, X. Experiment Research on Power Generation Performance of Double Piezoelectric Vibration Energy Harvester. IOP Conf. Ser. Mater. Sci. Eng. 2017, 269, 012094. [Google Scholar] [CrossRef]
- Guan, M.; Liao, W.H. Design and Analysis of a Piezoelectric Energy Harvester for Rotational Motion System. Energy Convers. Manag. 2016, 111, 239–244. [Google Scholar] [CrossRef]
- Garg, A.; Dwivedy, S.K. Piezoelectric Energy Harvester under Parametric Excitation: A Theoretical and Experimental Investigation. J. Intell. Mater. Syst. Struct. 2020, 31, 612–631. [Google Scholar] [CrossRef]
- Fu, H.; Yeatman, E.M. Rotational Energy Harvesting Using Bi-Stability and Frequency up-Conversion for Low-Power Sensing Applications: Theoretical Modelling and Experimental Validation. Mech. Syst. Signal Process. 2019, 125, 229–244. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A Comprehensive Review on the State-of-the-Art of Piezoelectric Energy Harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Covaci, C.; Gontean, A. Piezoelectric Energy Harvesting Solutions: A Review. Sensors 2020, 20, 3512. [Google Scholar] [CrossRef] [PubMed]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A Review of Energy Harvesting Using Piezoelectric Materials: State-of-the-Art a Decade Later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Sarker, M.R.; Julai, S.; Sabri, M.F.M.; Said, S.M.; Islam, M.M.; Tahir, M. Review of Piezoelectric Energy Harvesting System and Application of Optimization Techniques to Enhance the Performance of the Harvesting System. Sens. Actuators A Phys. 2019, 300, 111634. [Google Scholar] [CrossRef]
- Moosavian, A.; Khazaee, M.; Ahmadi, H.; Khazaee, M.; Najafi, G. Fault Diagnosis and Classification of Water Pump Using Adaptive Neuro-Fuzzy Inference System Based on Vibration Signals. Struct. Health Monit. 2015, 14, 402–410. [Google Scholar] [CrossRef]
- Moosavian, A.; Ahmadi, H.; Tabatabaeefar, A.; Khazaee, M. Comparison of Two Classifiers; K-Nearest Neighbor and Artificial Neural Network, for Fault Diagnosis on a Main Engine Journal-Bearing. Shock Vib. 2013, 20, 263–272. [Google Scholar] [CrossRef]
- Moosavian, A.; Jafari, S.M.; Khazaee, M.; Ahmadi, H. A Comparison Between ANN, SVM and Least Squares SVM: Application in Multi-Fault Diagnosis of Rolling Element Bearing. Int. J. Acoust. Vib. 2018, 23, 432. [Google Scholar]
- Khazaee, M.; Rezania, A.; Rosendahl, L. Effect of Damage and Support Damping Mechanisms on Unimorph Piezoelectric Energy Harvester. J. Vib. Control 2019, 25, 2409–2422. [Google Scholar] [CrossRef]
- Priya, S. Advances in Energy Harvesting Using Low Profile Piezoelectric Transducers. J. Electroceram. 2007, 19, 165–182. [Google Scholar] [CrossRef]
- Khazaee, M.; Huber, J.E.; Rosendahl, L.; Rezania, A. On the Determination of Viscous and Structural Damping Coefficients for Piezoelectric Energy Harvesters Using Only Time-Domain Voltage Measurements. Appl. Energy 2021, 285, 116427. [Google Scholar] [CrossRef]
- Torah, R.N.; Tudor, M.J.; Patel, K.; Garcia, I.N.; Beeby, S.P. Autonomous Low Power Microsystem Powered by Vibration Energy Harvesting. In Proceedings of the IEEE Sensors, Atlanta, GA, USA, 28–31 October 2007; pp. 264–267. [Google Scholar] [CrossRef]
- Owen, T.H.; Kestermann, S.; Torah, R.; Beeby, S.P. Self Powered Wireless Sensors for Condition Monitoring Applications. Sens. Rev. 2009, 29, 38–43. [Google Scholar] [CrossRef]
- Roundy, S.; Leland, E.S.; Baker, J.; Carleton, E.; Reilly, E.; Lai, E.; Otis, B.; Rabaey, J.M.; Wright, P.K.; Sundararajan, V. Improving Power Output for Vibration-Based Energy Scavengers. IEEE Pervasive Comput. 2005, 4, 28–36. [Google Scholar] [CrossRef]
- Otis, B.P.; Rabaey, J.M. A 300μmW 1.9GHz CMOS Oscillator Utilizing Micromachined Resonators. Eur. Solid-State Circuits Conf. 2002, 38, 151–154. [Google Scholar]
- Khazaee, M.; Rezania, A.; Rosendahl, L. An Experimental Study to Determine Damping of Piezoelectric Harvesters Using Transient Analysis of Unified Electromechanical Voltage Equation. Energy Convers. Manag. 2021, 227, 113567. [Google Scholar] [CrossRef]
- Piezo.com Products Datasheet & User Manual. Available online: https://piezo.com/collections/piezoelectric-actuators-motors/products/piezoelectric-bending-transducer-q220-h4br-2513yb (accessed on 23 July 2021).
- Khazaee, M.; Rezaniakolaei, A.; Rosendahl, L. A Comprehensive Electromechanically Coupled Model for Non-Uniform Piezoelectric Energy Harvesting Composite Laminates. Mech. Syst. Signal Process. 2020, 145, 106927. [Google Scholar] [CrossRef]
- Augustyn, D.; Cosack, N.; Ulriksen, M.D. On the Influence of Environmental and Operational Variability on Modal Parameters of Offshore Wind Support Structures. Mar. Struct. 2022, 84, 103185. [Google Scholar] [CrossRef]
- Butt, Z.; Pasha, R.A. Effect of Temperature and Loading on Output Voltage of Lead Zirconate Titanate (PZT-5A) Piezoelectric Energy Harvester. IOP Conf. Ser. Mater. Sci. Eng. 2016, 146, 012016. [Google Scholar] [CrossRef] [Green Version]
- Hirst, J.; Wang, J.; Nabawy, M.R.A.; Cioncolini, A. Long-Term Power Degradation Testing of Piezoelectric Vibration Energy Harvesters for Low-Frequency Applications. Eng. Res. Express 2020, 2, 035026. [Google Scholar] [CrossRef]























| Fault Type | Frequency Shift (Hz) | Vibration Amplitude Change (%) |
|---|---|---|
| Bearing corrosion [7] | −2.16 | 100.4% |
| Separator damage [7] | +0.80 | 59.0% |
| Hot temperature [7] | +0.61 | 86.9% |
| Without lubricant [7] | 1.85 | 66.1% |
| Shaft misalignment [28] | 0.0 | 200.0% |
| Shaft looseness [28] | 0.0 | 48.2% |
| Broken rotor bar [2] | ±4.35 | N/A |
| Bearing defect (hole in case) [2] | +120 | N/A |
| Bent shaft [3] | 0.0 | 351.0% |
| Definition | Definition | |||
|---|---|---|---|---|
| Series connection | ||||
| Parallel connection | ||||
| Series connection | ||||
| Parallel connection | ||||
| Natural Frequency (Hz) | Datasheet [39] | Finite Element [40] | Present Model (from Table 2) |
|---|---|---|---|
| No tip mass | 78.0 | 79.2 | 79.3 |
| 8.9-g tip mass | N/A | 32.5 | 33.6 |
| fr, Rotation Speed (Hz) | 9.5 | 11.5 | 14.9 | 17.83 | 18.3 | 20.75 | 22.95 |
|---|---|---|---|---|---|---|---|
| Generated power with R = 110 kΩ, µW | 99.0 | 256.5 | 401.3 | 1581.6 | 1029.2 | 238.3 | 236.5 |
| Minimum required number of PGs | 8 | 4 | 2 | 1 | 1 | 4 | 4 |
| The number of required PGs | 8 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khazaee, M.; Rosendahl, L.A.; Rezania, A. Online Condition Monitoring of Rotating Machines by Self-Powered Piezoelectric Transducer from Real-Time Experimental Investigations. Sensors 2022, 22, 3395. https://doi.org/10.3390/s22093395
Khazaee M, Rosendahl LA, Rezania A. Online Condition Monitoring of Rotating Machines by Self-Powered Piezoelectric Transducer from Real-Time Experimental Investigations. Sensors. 2022; 22(9):3395. https://doi.org/10.3390/s22093395
Chicago/Turabian StyleKhazaee, Majid, Lasse Aistrup Rosendahl, and Alireza Rezania. 2022. "Online Condition Monitoring of Rotating Machines by Self-Powered Piezoelectric Transducer from Real-Time Experimental Investigations" Sensors 22, no. 9: 3395. https://doi.org/10.3390/s22093395
APA StyleKhazaee, M., Rosendahl, L. A., & Rezania, A. (2022). Online Condition Monitoring of Rotating Machines by Self-Powered Piezoelectric Transducer from Real-Time Experimental Investigations. Sensors, 22(9), 3395. https://doi.org/10.3390/s22093395