Informer-Based Temperature Prediction Using Observed and Numerical Weather Prediction Data
Abstract
:1. Introduction
2. Deep-Learning-Based Temperature Prediction Methods
3. Datasets and Conventional Methods
3.1. Datasets
3.2. Conventional Methods
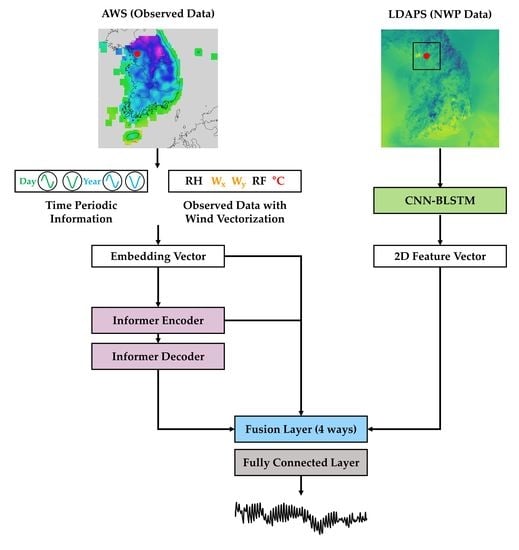
4. Proposed Temperature Prediction Model
4.1. Pre-Processing
4.2. Informer-Based Temperature Prediction Using Observed Data
4.3. Informer Fusion with CNN–BLSTM Using NWP
5. Experiments and Discussion
5.1. Experimental Setup
5.2. Performance Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Korean Meteorological Agency. Weather Forecast. Available online: https://web.kma.go.kr/eng/biz/forecast_01.jsp (accessed on 10 February 2023).
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Chang, F.-J.; Chang, L.-C.; Kao, I.-F.; Wang, Y.-S. Explore a deep learning multi-output neural network for regional multi-step-ahead air quality forecasts. J. Clean. Prod. 2019, 209, 134–145. [Google Scholar] [CrossRef]
- Ghaderi, A.; Sanandaji, B.M.; Ghaderi, F. Deep forecast: Deep learning-based spatio-temporal forecasting. arXiv 2017, arXiv:1707.08110. [Google Scholar] [CrossRef]
- Bedi, J.; Toshniwal, D. Deep learning framework to forecast electricity demand. Appl. Energy 2019, 238, 1312–1326. [Google Scholar] [CrossRef]
- Cao, Q.; Ewing, B.T.; Thompson, M.A. Forecasting wind speed with recurrent neural networks. Eur. J. Oper. Res. 2012, 221, 148–154. [Google Scholar] [CrossRef]
- Franch, G.; Nerini, D.; Pendesini, M.; Coviello, L.; Jurman, G.; Furlanello, C. Precipitation nowcasting with orographic enhanced stacked generalization: Improving deep learning predictions on extreme events. Atmosphere 2020, 11, 267. [Google Scholar] [CrossRef] [Green Version]
- Jebli, I.; Belouadha, F.Z.; Kabbaj, M.I.; Tilioua, A. Deep learning based models for solar energy prediction. Adv. Sci. Technol. Eng. Syst. J. 2021, 6, 349–355. [Google Scholar] [CrossRef]
- Du, S.; Li, T.; Yang, Y.; Horng, S.J. Deep air quality forecasting using hybrid deep learning framework. IEEE Trans. Knowl. Data Eng. 2019, 33, 2412–2424. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Wang, H.; Dong, J.; Zhong, G.; Sun, X. Prediction of sea surface temperature using long short-term memory. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1745–1749. [Google Scholar] [CrossRef] [Green Version]
- Altan, A.; Karasu, S.; Zio, E. A new hybrid model for wind speed forecasting combining long short-term memory neural network, decomposition methods and grey wolf optimizer. Appl. Soft Comput. 2021, 100, 106996. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient Transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 8–9 February 2021; pp. 11106–11115. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. Available online: https://dl.acm.org/doi/10.5555/3295222.3295349 (accessed on 1 July 2023).
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF ensemble prediction system: Methodology and validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Wilson, D.R.; Ballard, S.P. A microphysically based precipitation scheme for the UK meteorological office unified model. Q. J. R. Meteorol. Soc. 1999, 125, 1607–1636. [Google Scholar] [CrossRef]
- Stensrud, D.J. Parameterization Schemes: Keys to Understanding Numerical Weather Prediction Models; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Al-Yahyai, S.; Charabi, Y.; Gastli, A. Review of the use of numerical weather prediction (NWP) models for wind energy assessment. Renew. Sustain. Energy Rev. 2010, 14, 3192–3198. [Google Scholar] [CrossRef]
- University Corporation for Atmospheric Research. Understanding Assimilation Systems: How Models Create Their Initial Conditions—Version 2. Available online: https://www.meted.ucar.edu/training_module.php?id=704 (accessed on 9 July 2023).
- University Corporation for Atmospheric Research. NWP Model Fundamentals—Version 2. Available online: https://www.meted.ucar.edu/training_module.php?id=700 (accessed on 9 July 2023).
- Lynch, P. The Emergence of Numerical Weather Prediction: Richardson’s Dream; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Temam, R. Navier–Stokes Equations: Theory and Numerical Analysis; American Mathematical Society: Providence, RI, USA, 2001. [Google Scholar]
- Espeholt, L.; Agrawal, S.; Sønderby, C.; Kumar, M.; Heek, J.; Bromberg, C.; Gazen, C.; Carver, R.; Andrychowicz, M.; Hickey, J.; et al. Deep learning for twelve hour precipitation forecasts. Nat. Commun. 2022, 13, 5145. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, S.; Barrington, L.; Bromberg, C.; Burge, J.; Gazen, C.; Hickey, J. Machine learning for precipitation nowcasting from radar images. arXiv 2019, arXiv:1912.12132. [Google Scholar] [CrossRef]
- Fu, Q.; Niu, D.; Zang, Z.; Huang, J.; Diao, L. Multi-stations’ weather prediction based on hybrid model using 1D CNN and Bi-LSTM. In Proceedings of the 38th Chinese Control Conference, Guangzhou, China, 27–30 July 2019; IEEE: New York, NY, USA, 2019; pp. 3771–3775. [Google Scholar] [CrossRef]
- Han, L.; Sun, J.; Zhang, W. Convolutional neural network for convective storm nowcasting using 3-D doppler weather radar data. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1487–1495. [Google Scholar] [CrossRef]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5622–5632. Available online: https://dl.acm.org/doi/10.5555/3295222.3295313 (accessed on 1 July 2023).
- Sønderby, C.K.; Espeholt, L.; Heek, J.; Dehghani, M.; Oliver, A.; Salimans, T.; Agrawal, S.; Hickey, J.; Kalchbrenner, N. Metnet: A neural weather model for precipitation forecasting. arXiv 2020, arXiv:2003.12140. [Google Scholar] [CrossRef]
- Espeholt, L.; Agrawal, S.; Sønderby, C.; Kumar, M.; Heek, J.; Bromberg, C.; Gazen, C.; Hickey, J.; Bell, A.; Kalchbrenner, N. Skillful twelve hour precipitation forecasts using large context neural networks. arXiv 2021, arXiv:2111.07470. [Google Scholar] [CrossRef]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef]
- Wu, Q.; Guan, F.; Lv, C.; Huang, Y. Ultra-short-term multi-step wind power forecasting based on CNN-LSTM. IET Renew. Power Gener. 2021, 15, 1019–1029. [Google Scholar] [CrossRef]
- Chen, R.; Wang, X.; Zhang, W.; Zhu, X.; Li, A.; Yang, C. A hybrid CNN-LSTM model for typhoon formation forecasting. GeoInformatica 2019, 23, 375–396. [Google Scholar] [CrossRef]
- Jeong, S.; Park, I.; Kim, H.S.; Song, C.H.; Kim, H.K. Temperature prediction based on bidirectional long short-term memory and convolutional neural network combining observed and numerical forecast data. Sensors 2021, 21, 941. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with auto-correlation for long-term series forecasting. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS), Virtual, 6–14 December 2019; pp. 22419–22430. [Google Scholar] [CrossRef]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient Transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, P.; Li, Y.; Wen, L.; Deng, X. Air quality prediction models based on meteorological factors and real-time data of industrial waste gas. Sci. Rep. 2022, 12, 9253. [Google Scholar] [CrossRef] [PubMed]
- Park, I.; Kim, H.S.; Lee, J.; Kim, J.H.; Song, C.H.; Kim, H.K. Temperature prediction using the missing data refinement model based on a long short-term memory neural network. Atmosphere 2019, 10, 718. [Google Scholar] [CrossRef] [Green Version]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS), Sardinia, Italy, 13–15 March 2010; pp. 249–256. [Google Scholar]
- Kingma, D.P.; Ba, J. A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 2–5. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar] [CrossRef]
- Challu, C.; Olivares, K.G.; Oreshkin, B.N.; Garza, F.; Mergenthaler, M.; Dubrawski, A. N-hits: Neural hierarchical interpolation for time series forecasting. arXiv 2022, arXiv:2201.12886. [Google Scholar] [CrossRef]







| Model | Horizontal Resolution (Vertical Layers) | Number of Variables (Isobaric/Single) | Forecast Period (H) | Forecast Cycle (H) | Number of Prediction per Day | Grid Size (Coordinates) |
|---|---|---|---|---|---|---|
| GDAPS | 0.3515625° (70) | 7/101 | 0~84 90~288 | 3 6 | 8 4 | 1024 × 769 (0° E, 90° N) |
| RDAPS | 12 km (70) | 9/101 | 0~87 | 6 | 4 | 491 × 419 (101.577323° E, 12.217029° N) |
| LDAPS | 1.5 km (70) | 8/78 | 36 | 3 | 8 | 602 × 781 (121.834429° E, 32.256875° N) |
| Time (H) | Metric | BLSTM | Informer |
|---|---|---|---|
| 6 | RMSE | 2.38 | 1.62 |
| MAE | 1.75 | 1.20 | |
| 12 | RMSE | 2.70 | 2.39 |
| MAE | 1.96 | 1.90 | |
| 24 | RMSE | 3.05 | 2.92 |
| MAE | 2.28 | 2.26 | |
| 72 | RMSE | 3.83 | 3.27 |
| MAE | 2.94 | 2.53 | |
| 168 | RMSE | 4.08 | 3.74 |
| MAE | 3.14 | 2.91 | |
| 336 | RMSE | 4.42 | 4.05 |
| MAE | 3.40 | 3.15 |
| Time (H) | Metric | CNN–BLSTM Fusion Model [32] | Informer Fusion Model | |||
|---|---|---|---|---|---|---|
| Embedding Addition | Encoder | Decoder | Encoder Decoder | |||
| 6 | RMSE | 0.92 | 1.69 | 0.86 | 0.97 | 0.85 |
| MAE | 0.72 | 1.28 | 0.68 | 0.78 | 0.67 | |
| 12 | RMSE | 1.62 | 2.62 | 1.21 | 1.44 | 1.15 |
| MAE | 1.23 | 2.07 | 0.93 | 1.13 | 0.89 | |
| 24 | RMSE | 1.98 | 2.93 | 1.73 | 2.15 | 1.91 |
| MAE | 1.49 | 2.22 | 1.30 | 1.60 | 1.39 | |
| 72 | RMSE | 3.14 | 3.81 | 2.99 | 3.27 | 3.22 |
| MAE | 2.42 | 2.90 | 2.27 | 2.42 | 2.41 | |
| 168 | RMSE | 3.74 | 4.50 | 3.47 | 4.23 | 4.36 |
| MAE | 2.88 | 3.58 | 2.59 | 3.35 | 3.36 | |
| 336 | RMSE | 4.26 | 4.88 | 3.97 | 4.97 | 4.72 |
| MAE | 3.29 | 3.94 | 3.09 | 3.95 | 3.83 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jun, J.; Kim, H.K. Informer-Based Temperature Prediction Using Observed and Numerical Weather Prediction Data. Sensors 2023, 23, 7047. https://doi.org/10.3390/s23167047
Jun J, Kim HK. Informer-Based Temperature Prediction Using Observed and Numerical Weather Prediction Data. Sensors. 2023; 23(16):7047. https://doi.org/10.3390/s23167047
Chicago/Turabian StyleJun, Jimin, and Hong Kook Kim. 2023. "Informer-Based Temperature Prediction Using Observed and Numerical Weather Prediction Data" Sensors 23, no. 16: 7047. https://doi.org/10.3390/s23167047
APA StyleJun, J., & Kim, H. K. (2023). Informer-Based Temperature Prediction Using Observed and Numerical Weather Prediction Data. Sensors, 23(16), 7047. https://doi.org/10.3390/s23167047