Extraction of Roads Using the Archimedes Tuning Process with the Quantum Dilated Convolutional Neural Network
Abstract
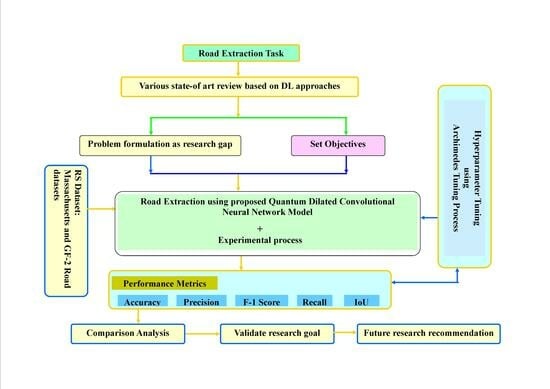
:1. Introduction
2. Related Works
- The limited investigation of quantum-inspired methodologies for the extraction of road features from remote sensing images.
- The proposed ATP-QDCNNRE method described in Section 3.1 attempts to address the integration of quantum-inspired dilated convolutions, exploring quantum computing concepts and optimizing dilated convolutions for long-range dependencies for road extraction from road datasets.
- Failures in the efficient use of dilated convolutions and automated hyperparameter modifications to achieve good road semantic segmentation using deep learning models. Employing automated hyperparameter tuning in Section 3.2, and developing a fully automated road extraction system.
- The proposed ATP-QDCNNRE method attempts to address the integration of quantum-inspired dilated convolutions, explore quantum computing concepts, optimize dilated convolutions for long-range dependencies, employ automated hyperparameter tuning, and develop a fully automated road extraction system.
- The study performs experiments utilizing the Massachusetts road dataset to showcase the enhanced performance of the QDCNN model.
| Authors [Citations] | Year | Methodology | Challenges |
|---|---|---|---|
| Tao, J et al. [62] | 2023 | SegNet; Road extraction based on transformer and CNN with connectivity structures. | Narrowness, complex shape, and broad span of roads in the RS images; the results are often unsatisfactory. |
| Yin, A et al. [63] | 2023 | HRU-Net: High-resolution remote sensing image road extraction based on multi-scale fusion | Shadow, occlusion, and spectral confusion hinder the accuracy and consistency of road extraction in satellite images. |
| Shao, S et al. [35] | 2022 | Road extraction based on channel attention mechanism and spatial attention mechanism were introduced to enhance the use of spectral information and spatial information based on the U-Net framework | To solve the problem of automatic extraction of road networks from a large number of remote sensing images. |
| Jie, Y et al. [64] | 2022 | MECA-Net is a novel approach for road extraction from remote sensing images. It incorporates a multi-scale feature encoding mechanism and a long-range context-aware network. | The scale disparity of roads in remote sensing imagery exhibits significant variation, with the identification of narrow roadways posing a challenging task. Furthermore, it is worth noting that the road depicted in the image frequently encounters obstruction caused by the shadows cast by surrounding trees and buildings. This, in turn, leads to the extraction results being fragmented and incomplete. |
| Li, J et al. [65] | 2021 | Proposed an innovative cascaded attention DenseUNet (CADUNet) semantic segmentation model by embedding two attention modules, such as global attention and core attention modules | To preserve the integrity of smoothness of the sideline and maintain the connectedness of the road network; also to identify and account for any occlusion caused by roadside tree canopies or high-rise buildings. |
| Wu, Q et al. [66] | 2020 | Based on densely connected spatial feature-enhanced pyramid method | Loss of multiscale spatial feature. |
| Authors | Results Based on Various Parameters Used by Authors | |||||
|---|---|---|---|---|---|---|
| Overall Accuracy (%) | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) | |
| Tao, J et al. [62] | -- | -- | 87.34 | 92.86 | 90.02 | 68.38 |
| Yin, A et al. [63] | -- | -- | 80.09 | 84.85 | 82.40 | 78.62 |
| Shao, S et al. [35] | -- | 98.90 | 78.40 | 77.00 | 76.40 | 63.10 |
| Jie, Y et al. [64] | -- | -- | 78.39 | 79.41 | 89.90 | 65.15 |
| Li, J et al. [65] | 98.00 | -- | 79.45 | 76.55 | 77.89 | 64.12 |
| Wu, Q et al. [66] | -- | -- | 90.09 | 88.11 | 89.09 | 80.39 |
3. The Proposed Methodology
3.1. Road Extraction Using QDCNN Model
3.1.1. Convolutional Layer
3.1.2. Dilatable Convolution
3.1.3. Fundamentally Different Quantum Convolution by Quanvolutional Filter
- Encoder model: At present, the data are encoded to a quantum state, and the encoded data are examined using QC circuits. One of the variable encoding methods that can be exploited to encode information is the Hadamard gate (H). The encoder function represented by transforms an initial state into a uniform superposition state i, specifically focusing on the data vector.
- Entanglement state: The encoder quantum state generated in the preceding model element has an effect on the single- and multi-qubit gates inside this module. Commonly utilized multi-qubit gates in quantum computing encompass CNOT gates and parametrically controlled rotation. The utilization of both single-qubit and multi-qubit gates in a composite manner results in the formation of parameterized layers. These layers can be further optimized to acquire assignment properties. If the unitary operations of the entanglement modules are all denoted by , then the resulting quantum state can be represented as follows:
- Decoder model: Subsequently, local variables, such as the Pauli operator, are estimated for the previous modules. The predictable value of local variables is attained by the following equation:
3.1.4. Network Design of (Quantum Circuit) Quanvolutional Layer
- assign the variable p to represent an arbitrary integer value, denoting the number of quanvolutional filters in a specific quanvolutional layer;
- add multiple additional quanvolutional layers on top of any existing layer within the network architecture.
3.2. Hyperparameter Tuning Using ATP
4. Data and Results
4.1. Data Collection
The Massachusetts Road Dataset and Its Preprocessing
4.2. Experimental Results
4.2.1. Evaluation Method
4.2.2. Experimental Result Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, H.; He, H.; Zhang, Y.; Ma, L.; Li, J. A comparative study of loss functions for road segmentation in remotely sensed road datasets. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103159. [Google Scholar] [CrossRef]
- Chen, W.; Zhou, G.; Liu, Z.; Li, X.; Zheng, X.; Wang, L. NIGAN: A framework for mountain road extraction integrating remote sensing road-scene neighborhood probability enhancements and improved conditional generative adversarial network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5626115. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, C.; Li, J.; Fan, W.; Du, J.; Zhong, B. Adaboost-like End-to-End multiple lightweight U-nets for road extraction from optical remote sensing images. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102341. [Google Scholar] [CrossRef]
- Behera, T.K.; Bakshi, S.; Sa, P.K.; Nappi, M.; Castiglione, A.; Vijayakumar, P.; Gupta, B.B. The NITRDrone dataset to address the challenges for road extraction from aerial images. J. Signal Process. Syst. 2023, 95, 197–209. [Google Scholar] [CrossRef]
- Sultonov, F.; Park, J.H.; Yun, S.; Lim, D.W.; Kang, J.M. Mixer U-Net: An improved automatic road extraction from UAV imagery. Appl. Sci. 2022, 12, 1953. [Google Scholar] [CrossRef]
- Bayramoğlu, Z.; Melis, U.Z.A.R. Performance analysis of rule-based classification and deep learning method for automatic road extraction. Int. J. Eng. Geosci. 2023, 8, 83–97. [Google Scholar] [CrossRef]
- Li, J.; Meng, Y.; Dorjee, D.; Wei, X.; Zhang, Z.; Zhang, W. Automatic road extraction from remote sensing imagery using ensemble learning and postprocessing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10535–10547. [Google Scholar] [CrossRef]
- Khan, M.J.; Singh, P.P. Advanced Road Extraction using CNN-based U-Net Model and Satellite Imagery. E-Prime-Adv. Electr. Eng. Electron. Energy 2023, 5, 100244. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, L.; Luo, Y.; Li, D.; Junior, J.M.; Gonçalves, W.N.; Nurunnabi, A.A.M.; Li, J.; Wang, C.; Li, D. Road extraction in remote sensing data: A survey. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102833. [Google Scholar] [CrossRef]
- Khan, M.J.; Singh, P.P. Road Extraction from Remotely Sensed Data: A Review. AIJR Proc. 2021, 106–111. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.155. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Girshick, R. Fast R-CNN 2015. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Boston, MA, USA, 7–12 June 2015; pp. 1440–1448. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- He, K.; Gkioxari, G.; Doll, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the 2015 International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the 2018 European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Sarker, I.H. Machine learning: Algorithms, real-world applications and research directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar]
- Kerenidis, L.; Landman, J.; Luongo, A.; Prakash, A. q-means: A quantum algorithm for unsupervised machine learning. arXiv 2018, arXiv:1812.03584. [Google Scholar]
- Otterbach, J.; Manenti, R.; Alidoust, N.; Bestwick, A.; Block, M.; Caldwell, S.; Didier, N.; Fried, E.S.; Hong, S.; Karalekas, P. Unsupervised machine learning on a hybrid quantum computer. arXiv 2017, arXiv:1712.05771. [Google Scholar]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum principal component analysis. Nat. Phys. 2013, 10, 7. [Google Scholar] [CrossRef]
- Liu, J.; Lim, K.H.; Wood, K.L.; Huang, W.; Guo, C.; Huang, H.-L. Hybrid quantum-classical convolutional neural networks. arXiv 2019, arXiv:1911.02998. [Google Scholar] [CrossRef]
- Cong, I.; Choi, S.; Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 2019, 15, 1273–1278. [Google Scholar] [CrossRef]
- Henderson, M.; Shakya, S.; Pradhan, S.; Cook, T. Quanvolutional neural networks: Powering image recognition with quantum circuits. Quantum Mach. Intell. 2020, 2, 2. [Google Scholar] [CrossRef]
- Oh, S.; Choi, J.; Kim, J. A tutorial on quantum convolutional neural networks (qcnn). In Proceedings of the 2020 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 19–21 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 236–239. [Google Scholar]
- Chen, S.Y.C.; Wei, T.C.; Zhang, C.; Yu, H.; Yoo, S. Quantum convolutional neural networks for high energy physics data analysis. arXiv 2020, arXiv:2012.12177. [Google Scholar] [CrossRef]
- Houssein, E.H.; Abohashima, Z.; Elhoseny, M.; Mohamed, W.M. Hybrid quantum convolutional neural networks model for COVID-19 prediction using chest x-ray images. arXiv 2021, arXiv:2102.06535. [Google Scholar] [CrossRef]
- Alam, M.; Kundu, S.; Topaloglu, R.O.; Ghosh, S. Iccad special session paper: Quantum-classical hybrid machine learning for image classification. arXiv 2021, arXiv:2109.02862. [Google Scholar]
- Yang, M.; Yuan, Y.; Liu, G. SDUNet: Road extraction via spatial enhanced and densely connected UNet. Pattern Recognit. 2022, 126, 108549. [Google Scholar] [CrossRef]
- Li, Y.; Xiang, L.; Zhang, C.; Jiao, F.; Wu, C. A Guided Deep Learning Approach for Joint Road Extraction and Intersection Detection from RS Images and Taxi Trajectories. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8008–8018. [Google Scholar] [CrossRef]
- Shao, S.; Xiao, L.; Lin, L.; Ren, C.; Tian, J. Road Extraction Convolutional Neural Network with Embedded Attention Mechanism for Remote Sensing Imagery. Remote Sens. 2022, 14, 2061. [Google Scholar] [CrossRef]
- Dai, L.; Zhang, G.; Zhang, R. RADANet: Road augmented deformable attention network for road extraction from complex high-resolution remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5602213. [Google Scholar] [CrossRef]
- Li, S.; Liao, C.; Ding, Y.; Hu, H.; Jia, Y.; Chen, M.; Xu, B.; Ge, X.; Liu, T.; Wu, D. Cascaded residual attention enhanced road extraction from remote sensing images. ISPRS Int. J. Geo-Inf. 2022, 11, 9. [Google Scholar] [CrossRef]
- Yan, J.; Ji, S.; Wei, Y. A combination of convolutional and graph neural networks for regularized road surface extraction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Rajamani, T.; Sevugan, P.; Ragupathi, S. Automatic building footprint extraction and road detection from hyper-spectral imagery. J. Electron. Imaging 2023, 32, 011005. [Google Scholar]
- Wang, Y.; Peng, Y.; Li, W.; Alexandropoulos, G.C.; Yu, J.; Ge, D.; Xiang, W. DDU-Net: Dual-decoder-U-Net for road extraction using high-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4409113. [Google Scholar] [CrossRef]
- Wan, J.; Xie, Z.; Xu, Y.; Chen, S.; Qiu, Q. DA-RoadNet: A dual-attention network for road extraction from high resolution satellite imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6302–6315. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, Z.; Zhang, T.; Li, Y. C-UNet: Complement UNet for remote sensing road extraction. Sensors 2021, 21, 2153. [Google Scholar] [CrossRef] [PubMed]
- Linnainmaa, S. Taylor expansion of the accumulated rounding error. BIT Numer. Math. 1976, 16, 146–160. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Pramanik, S.; Chandra, M.G.; Sridhar, C.V.; Kulkarni, A.; Sahoo, P.; Vishwa, C.D.; Sharma, H.; Navelkar, V.; Poojary, S.; Shah, P.; et al. A quantum-classical hybrid method for image classification and segmentation. arXiv 2021, arXiv:2109.14431. [Google Scholar]
- Hur, T.; Kim, L.; Park, D.K. Quantum convolutional neural network for classical data classification. arXiv 2021, arXiv:2108.00661. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Quantum machine learning in feature hilbert spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef]
- Mattern, D.; Martyniuk, D.; Willems, H.; Bergmann, F.; Paschke, A. Variational quanvolutional neural networks with enhanced image encoding. arXiv 2021, arXiv:2106.07327. [Google Scholar]
- Schuld, M.; Petruccione, F. Supervised Learning with Quantum Computers; Springer: Berlin/Heidelberg, Germany, 2018; Volume 17. [Google Scholar]
- LaRose, R.; Coyle, B. Robust data encodings for quantum classifiers. Phys. Rev. A 2020, 102, 032420. [Google Scholar] [CrossRef]
- Wang, Y.; Kuang, N.; Zheng, J.; Xie, P.; Wang, M.; Zhao, C. Dilated Convolutional Network for Road Extraction in Remote Sensing Images. In Advances in Brain In-spired Cognitive Systems, Proceedings of the 10th International Conference, BICS 2019, Guangzhou, China, 13–14 July 2019; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; Proceedings 10; pp. 263–272. [Google Scholar]
- Holschneider, M.; Kronland-Martinet, R.; Morlet, J.; Tchamitchian, P. A real-time algorithm for signal analysis with the help of the wavelet transform. In Wavelets, Time-Frequency Methods and Phase Space; Springer: Berlin/Heidelberg, Germany, 1989; Volume 1, pp. 286–297. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2016, arXiv:1511.07122. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.P.; Yuille, A.L. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv 2015, arXiv:1412.7062. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Hamaguchi, R.; Fujita, A.; Nemoto, K.; Imaizumi, T.; Hikosaka, S. Effective use of dilated convolutions for segmenting small object instances in remote sensing imagery. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1442–1450. [Google Scholar]
- Kudo, Y.; Aoki, Y. Dilated convolutions for image classification and object localization. In Proceedings of the 2017 Fifteenth IAPR International Conference on Machine Vision Applications (MVA), Nagoya, Japan, 8–12 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 452–455. [Google Scholar]
- Chen, Y.; Guo, Q.; Liang, X.; Wang, J.; Qian, Y. Environmental sound classification with dilated convolutions. Appl. Acoust. 2019, 148, 123–132. [Google Scholar] [CrossRef]
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Conditional time series forecasting with convolutional neural networks. arXiv 2017, arXiv:1703.04691. [Google Scholar]
- Chen, Y.; Kang, Y.; Chen, Y.; Wang, Z. Probabilistic forecasting with temporal convolutional neural network. Neurocomputing 2020, 399, 491–501. [Google Scholar] [CrossRef]
- Tao, J.; Chen, Z.; Sun, Z.; Guo, H.; Leng, B.; Yu, Z.; Wang, Y.; He, Z.; Lei, X.; Yang, J. Seg-Road: A Segmentation Network for Road Extraction Based on Transformer and CNN with Connectivity Structures. Remote Sens. 2023, 15, 1602. [Google Scholar] [CrossRef]
- Yin, A.; Ren, C.; Yan, Z.; Xue, X.; Yue, W.; Wei, Z.; Liang, J.; Zhang, X.; Lin, X. HRU-Net: High-Resolution Remote Sensing Image Road Extraction Based on Multi-Scale Fusion. Appl. Sci. 2023, 13, 8237. [Google Scholar] [CrossRef]
- Jie, Y.; He, H.; Xing, K.; Yue, A.; Tan, W.; Yue, C.; Jiang, C.; Chen, X. MECA-Net: A MultiScale Feature Encoding and Long-Range Context-Aware Network for Road Extraction from Remote Sensing Images. Remote Sens. 2022, 14, 5342. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Zhang, Y.; Zhang, Y. Cascaded attention DenseUNet (CADUNet) for road extraction from very-high-resolution images. ISPRS Int. J. Geo-Inf. 2021, 10, 329. [Google Scholar] [CrossRef]
- Wu, Q.; Luo, F.; Wu, P.; Wang, B.; Yang, H.; Wu, Y. Automatic road extraction from high-resolution remote sensing images using a method based on densely connected spatial feature-enhanced pyramid. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 3–17. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussain, K.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 2021, 51, 1531–1551. [Google Scholar] [CrossRef]
- Bergholm, V.; Izaac, J.; Schuld, M.; Gogolin, C.; Ahmed, S.; Ajith, V.; Alam, M.S.; Alonso-Linaje, G.; AkashNarayanan, B.; Asadi, A.; et al. Pennylane: Automatic differentiation of hybrid quantum-classical computations. arXiv 2018, arXiv:1811.04968. [Google Scholar]
- Tenali, N.; Babu, G.R.M. HQDCNet: Hybrid Quantum Dilated Convolution Neural Network for detecting COVID-19 in the context of Big Data Analytics. Multimed. Tools Appl. 2023, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Hashim, F.A.; Khurma, R.A.; Albashish, D.; Amin, M.; Hussien, A.G. Novel hybrid of AOAP-BSA with double adaptive and random spare for global optimization and engineering problems. Alex. Eng. J. 2023, 73, 543–577. [Google Scholar] [CrossRef]
- Mnih, V. Machine Learning for Aerial Image Labeling; University of Toronto: Toronto, ON, Canada, 2013; p. 109. [Google Scholar]
- Suzuki, Y.; Kawase, Y.; Masumura, Y.; Hiraga, Y.; Nakadai, M.; Chen, J.; Nakanishi, K.M.; Mitarai, K.; Imai, R.; Tamiya, S.; et al. Qulacs: A fast and versatile quantum circuit simulator for research purpose. arXiv 2020, arXiv:2011.13524. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Oud, S. PennyLane Qulacs Plugin. [Online]. 2019. Available online: https://github.com/soudy/pennylane-qulacs (accessed on 10 August 2023).
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhou, L.; Zhang, C.; Wu, M. D-Linknet: Linknet with Pretrained Encoder and Dilated Convolution for High Resolution Satellite Imagery Road Extraction. In Proceedings of the 2018 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Yan, H.; Zhang, C.; Yang, J.; Wu, M.; Chen, J. Did-Linknet: Polishing D-Block with Dense Connection and Iterative Fusion for Road Extraction. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2186–2189. [Google Scholar]
- Mei, J.; Li, R.J.; Gao, W.; Cheng, M.M. CoANet: Connectivity Attention Network for Road Extraction from Satellite Imagery. IEEE Trans. Image Process. 2021, 30, 8540–8552. [Google Scholar] [CrossRef]
- Mari, A. Quanvolutional Neural Networks; PennyLane; Xanadu: Toronto, ON, Canada, 2021. [Google Scholar]













| Hyperparameter | Description |
|---|---|
| Quantum circuit depth | The depth of quantum circuits or layers in the network (3 quantum layers). |
| Quantum gate parameters | Parameters specific to quantum gates used in the model. Example: Gate time and type (e.g., CNOT, Hadamard). |
| Momentum qml.optimize. ArchimedesOptimizer | Momentum is a mathematical optimization method used to enhance convergence speed and stability during the training of machine learning models. The “qml.optimize. ArchimedesOptimizer” is a quantum optimization algorithm used for solving optimization problems on quantum devices. |
| Loss Function | The choice of loss function for semantic segmentation is cross-entropy loss. |
| Activation function | The type of activation function used in the network. ReLU and Sigmoid. |
| Learning rate | Controls the step size during optimization. |
| Model | IoU | MIoU | F1 Score | Precision | Recall | FPS |
|---|---|---|---|---|---|---|
| PSPNet [75] | 58.91 | 72.23 | 75.22 | 74.37 | 76.09 | 75 |
| D-LinkNet [76] | 61.45 | 75.72 | 80.61 | 78.77 | 82.53 | 96 |
| LinkNet34 [77] | 61.35 | 75.87 | 80.17 | 78.77 | 81.63 | 105 |
| CoANet [78] | 61.67 | 76.42 | 81.56 | 78.53 | 84.85 | 61 |
| CoANet-UB [78] | 64.96 | 80.92 | 88.67 | 85.37 | 92.24 | 40 |
| MECA-Net [64] | 65.15 | 82.32 | 78.90 | 78.39 | 79.41 | 89 |
| ATP-QDCNNRE (Ours) | 75.28 | 95.19 | 90.85 | 87.54 | 94.41 | 158 |
| Methods | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) |
|---|---|---|---|---|
| Baseline (DCNN) | 58.47 | 76.10 | 66.10 | 65.67 |
| DCNN + (Quanvolutional) QDCNNRE | 80.07 | 72.22 | 76.40 | 72.04 |
| Baseline + ATP-QDCNNRE | 87.54 | 94.41 | 90.85 | 75.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.J.; Singh, P.P.; Pradhan, B.; Alamri, A.; Lee, C.-W. Extraction of Roads Using the Archimedes Tuning Process with the Quantum Dilated Convolutional Neural Network. Sensors 2023, 23, 8783. https://doi.org/10.3390/s23218783
Khan MJ, Singh PP, Pradhan B, Alamri A, Lee C-W. Extraction of Roads Using the Archimedes Tuning Process with the Quantum Dilated Convolutional Neural Network. Sensors. 2023; 23(21):8783. https://doi.org/10.3390/s23218783
Chicago/Turabian StyleKhan, Mohd Jawed, Pankaj Pratap Singh, Biswajeet Pradhan, Abdullah Alamri, and Chang-Wook Lee. 2023. "Extraction of Roads Using the Archimedes Tuning Process with the Quantum Dilated Convolutional Neural Network" Sensors 23, no. 21: 8783. https://doi.org/10.3390/s23218783
APA StyleKhan, M. J., Singh, P. P., Pradhan, B., Alamri, A., & Lee, C. -W. (2023). Extraction of Roads Using the Archimedes Tuning Process with the Quantum Dilated Convolutional Neural Network. Sensors, 23(21), 8783. https://doi.org/10.3390/s23218783