Algorithm for Mobile Platform-Based Real-Time QRS Detection
Abstract
:1. Introduction
2. Methods
2.1. Algorithms
- (1)
- The Pan–Tompkins algorithm performs an analysis on two simultaneous signals: the bandpassed signal and the resulting filtered signal. The peaks from each signal are compared on a time basis for correspondence. However, with the AMPT algorithm, the signal peaks and the noise peaks from the bandpassed signal are not calculated and only the final filtered signal is analyzed.
- (2)
- The Pan–Tompkins algorithm uses two average RR intervals for search back (one for sinus rhythm and one for arrhythmias), which entails defining the signal and noise peaks, thresholds, and a series of RR limits. The AMPT does not differentiate based on regular or irregular rhythms, and therefore requires fewer computational steps because search back is calculated from a single averaged RR interval.
2.2. ECG Datasets
2.3. Analysis
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumari, P.; Mathew, L.; Syal, P. Increasing trend of wearables and multimodal interface for human activity monitoring: A review. Biosens. Bioelectron. 2017, 90, 298–307. [Google Scholar] [CrossRef] [PubMed]
- Mück, J.E.; Ünal, B.; Butt, H.; Yetisen, A.K. Market and Patent Analyses of Wearables in Medicine. Trends Biotechnol. 2019, 37, 563–566. [Google Scholar] [CrossRef] [PubMed]
- Dagher, L.; Shi, H.; Zhao, Y.; Marrouche, N.F. Wearables in cardiology: Here to stay. Heart Rhythm. 2020, 17, 889–895. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.J.; Jeong, H.; Cho, K.W.; Lu, N.; Kim, D.-H. Wearable and Implantable Devices for Cardiovascular Healthcare: From Monitoring to Therapy Based on Flexible and Stretchable Electronics. Adv. Funct. Mater. 2019, 29, 1808247. [Google Scholar] [CrossRef]
- Stehlik, J.; Schmalfuss, C.; Bozkurt, B.; Nativi-Nicolau, J.; Wohlfahrt, P.; Wegerich, S.; Rose, K.; Ray, R.; Schofield, R.; Deswal, A.; et al. Continuous Wearable Monitoring Analytics Predict Heart Failure Hospitalization. Circ. Heart Fail. 2020, 13, e006513. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. Fast QRS Detection with an Optimized Knowledge-Based Method: Evaluation on 11 Standard ECG Databases. PLoS ONE 2013, 8, e73557. [Google Scholar] [CrossRef] [PubMed]
- Manikandan, M.; Soman, K. A novel method for detecting R-peaks in electrocardiogram (ECG) signal. Biomed. Signal Process. Control. 2012, 7, 118–128. [Google Scholar] [CrossRef]
- Kim, J.; Shin, H. Simple and Robust Realtime QRS Detection Algorithm Based on Spatiotemporal Characteristic of the QRS Complex. PLoS ONE 2016, 11, e0150144. [Google Scholar] [CrossRef] [PubMed]
- Zalabarria, U.; Irigoyen, E.; Martinez, R.; Lowe, A. Online robust R-peaks detection in noisy electrocardiograms using a novel iterative smart processing algorithm. Appl. Math. Comput. 2020, 369, 124839. [Google Scholar] [CrossRef]
- El Bouny, L.; Khalil, M.; Adib, A. A Wavelet Denoising and Teager Energy Operator-Based Method for Automatic QRS Complex Detection in ECG Signal. Circuits Syst. Signal Process. 2020, 39, 4943–4979. [Google Scholar] [CrossRef]
- Farashi, S. A multiresolution time-dependent entropy method for QRS complex detection. Biomed. Signal Process. Control. 2016, 24, 63–71. [Google Scholar] [CrossRef]
- Li, C.; Zheng, C.; Tai, C. Detection of ECG characteristic points using wavelet transforms. IEEE Trans. Biomed. Eng. 1995, 42, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Legarreta, I.R.; Addison, P.; Grubb, N.; Clegg, G.; Robertson, C.; Fox, K.; Watson, J. R-Wave Detection Using Continuous Wavelet Modulus Maxima in Computers in Cardiology; IEEE: New York, NY, USA, 2003; pp. 565–568. [Google Scholar] [CrossRef]
- Yeh, Y.-C.; Wang, W.-J. QRS complexes detection for ECG signal: The Difference Operation Method. Comput. Methods Programs Biomed. 2008, 91, 245–254. [Google Scholar] [CrossRef] [PubMed]
- Madeiro, J.P.; Cortez, P.C.; Marques, J.A.; Seisdedos, C.R.; Sobrinho, C.R. An innovative approach of QRS segmentation based on first-derivative, Hilbert and Wavelet Transforms. Med. Eng. Phys. 2012, 34, 1236–1246. [Google Scholar] [CrossRef]
- Poli, R.; Cagnoni, S.; Valli, G. Genetic design of optimum linear and nonlinear QRS detectors. IEEE Trans. Biomed. Eng. 1995, 42, 1137–1141. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Zhang, Y.; Zhang, M.; Liu, W.; Chang, S.; Wang, H.; He, J.; Huang, Q. A Real Time QRS Detection Algorithm Based on ET and PD Controlled Threshold Strategy. Sensors 2020, 20, 4003. [Google Scholar] [CrossRef]
- Raj, S.; Ray, K.C.; Shankar, O. Development of robust, fast and efficient QRS complex detector: A methodological review. Australas. Phys. Eng. Sci. Med. 2018, 41, 581–600. [Google Scholar] [CrossRef]
- Kumar, A.; Komaragiri, R.; Kumar, M. From Pacemaker to Wearable: Techniques for ECG Detection Systems. J. Med. Syst. 2018, 42, 34. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Shabaan, M.; Arshid, K.; Yaqub, M.; Jinchao, F.; Zia, M.S.; Bojja, G.R.; Iftikhar, M.; Ghani, U.; Ambati, L.S.; Munir, R. Survey: Smartphone-based assessment of cardiovascular diseases using ECG and PPG analysis. BMC Med. Inform. Decis. Mak. 2020, 20, 177. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Eskofier, B.; Dokos, S.; Abbott, D. Revisiting QRS Detection Methodologies for Portable, Wearable, Battery-Operated, and Wireless ECG Systems. PLoS ONE 2014, 9, e84018. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Liu, C.; Jiang, X.; Zhang, Z.; Zhang, Y.; Li, J.; Wei, S. Performance Analysis of Ten Common QRS Detectors on Different ECG Application Cases. J. Health Eng. 2018, 2018, 9050812. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Yazicioglu, R.F.; Merken, P.; Van Hoof, C.; Yoo, H.-J. ECG Signal Compression and Classification Algorithm with Quad Level Vector for ECG Holter System. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Pickus, S. Pan-Tompkins. Available online: https://github.com/pickus91/HRV (accessed on 25 January 2023).
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed]
- TELE ECG Database: 250 telehealth ECG records (collected using dry metal electrodes) with annotated QRS and artifact masks, and MATLAB code for the UNSW artifact detection and UNSW QRS detection algorithms. Harv. Dataverse 2016. [CrossRef]
- Robust Detection of Heart Beats in Multimodal Data: The PhysioNet/Computing in Cardiology Challenge. 2014. Available online: https://archive.physionet.org/challenge/2014/ (accessed on 3 May 2022).
- T.A.L. The Beth Israel Deaconess Medical Center. The MIT-BIH Normal Sinus Rhythm Database. 1990. Available online: Physionet.org (accessed on 25 January 2023). [CrossRef]
- Moody, G.B.; Mark, R.G. MIT-BIH Arrhythmia Database. 1992. Available online: Physionet.org (accessed on 25 January 2023). [CrossRef]
- Association for the Advancement of Medical Instrumentation: Testing and Reporting Performance Results of Cardiac Rhythm and ST Segment Measurement Algorithms. ANSI/AAMI EC57. 2012. Available online: https://webstore.ansi.org/standards/aami/ansiaamiec572012ec57 (accessed on 25 January 2023).
- Hossain, B.; Bashar, S.K.; Walkey, A.J.; McManus, D.D.; Chon, K.H. An Accurate QRS Complex and P Wave Detection in ECG Signals Using Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Approach. IEEE Access 2019, 7, 128869–128880. [Google Scholar] [CrossRef]
- Khundaqji, H.; Hing, W.; Furness, J.; Climstein, M. Smart Shirts for Monitoring Physiological Parameters: Scoping Review. JMIR mHealth uHealth 2020, 8, e18092. [Google Scholar] [CrossRef]
- Gualandi, I.; Marzocchi, M.; Achilli, A.; Cavedale, D.; Bonfiglio, A.; Fraboni, B. Textile Organic Electrochemical Transistors as a Platform for Wearable Biosensors. Sci. Rep. 2016, 6, 33637. [Google Scholar] [CrossRef] [Green Version]


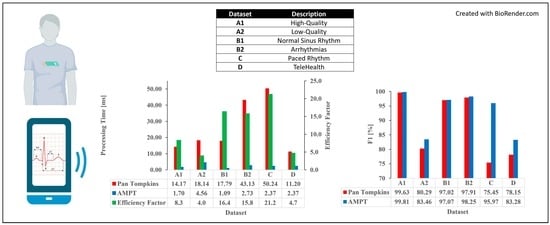
| Dataset | Description | Number of Beats | Number of Records | Record Length (min) | Total Time (min) | Sample Frequency (Hz) |
|---|---|---|---|---|---|---|
| A1 | High Quality | 72,415 | 100 | 10 | 1000 | 250 |
| A2 | Low Quality | 78,618 | 100 | 10 | 1000 | 360 |
| B1 | Normal Sinus Rhythm | 48,494 | 18 | 30 | 540 | 128 |
| B2 | Arrhythmias | 103,724 | 44 | 30 | 1320 | 360 |
| C | Paced Rhythm | 8923 | 4 | 30 | 120 | 360 |
| D | TeleHealth | 6708 | 134 | 0.5 | 125 | 500 |
| Dataset | Annotated Peaks | Algorithm | True Positives (Beats) | False Positives (Beats) | False Negatives (Beats) | Failed Detection (Beats) | Error Rate (%) | Sensitivity (%) | Positive Predictive Value (%) | Accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 72,415 | Pan–Tompkins | 72,073 | 191 | 348 | 539 | 0.74 | 99.51 | 99.75 | 99.26 |
| AMPT | 72,267 | 135 | 148 | 283 | 0.39 | 99.80 | 99.82 | 99.62 | ||
| A2 | 78,618 | Pan–Tompkins | 64,653 | 11137 | 14,065 | 25,202 | 32.06 | 80.75 | 85.12 | 74.09 |
| AMPT | 64,993 | 8671 | 13,639 | 22,310 | 28.38 | 82.06 | 86.37 | 78.54 | ||
| B1 | 48,494 | Pan–Tompkins | 45,231 | 134 | 2988 | 3122 | 6.44 | 95.08 | 99.74 | 94.85 |
| AMPT | 45,301 | 8 | 3083 | 3091 | 6.37 | 94.97 | 99.98 | 94.96 | ||
| B2 | 103,724 | Pan–Tompkins | 99,783 | 349 | 3720 | 4069 | 3.92 | 96.36 | 99.66 | 96.09 |
| AMPT | 100,135 | 144 | 3380 | 3524 | 3.40 | 96.80 | 99.83 | 96.66 | ||
| C | 8923 | Pan–Tompkins | 6684 | 2132 | 2238 | 4370 | 48.97 | 74.93 | 75.97 | 64.26 |
| AMPT | 8468 | 276 | 454 | 730 | 8.18 | 96.90 | 95.07 | 92.81 | ||
| D | 6708 | Pan–Tompkins | 3218 | 972 | 522 | 1494 | 40.10 | 84.92 | 77.56 | 68.91 |
| AMPT | 3394 | 707 | 334 | 1041 | 27.94 | 90.00 | 81.04 | 76.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neri, L.; Oberdier, M.T.; Augello, A.; Suzuki, M.; Tumarkin, E.; Jaipalli, S.; Geminiani, G.A.; Halperin, H.R.; Borghi, C. Algorithm for Mobile Platform-Based Real-Time QRS Detection. Sensors 2023, 23, 1625. https://doi.org/10.3390/s23031625
Neri L, Oberdier MT, Augello A, Suzuki M, Tumarkin E, Jaipalli S, Geminiani GA, Halperin HR, Borghi C. Algorithm for Mobile Platform-Based Real-Time QRS Detection. Sensors. 2023; 23(3):1625. https://doi.org/10.3390/s23031625
Chicago/Turabian StyleNeri, Luca, Matt T. Oberdier, Antonio Augello, Masahito Suzuki, Ethan Tumarkin, Sujai Jaipalli, Gian Angelo Geminiani, Henry R. Halperin, and Claudio Borghi. 2023. "Algorithm for Mobile Platform-Based Real-Time QRS Detection" Sensors 23, no. 3: 1625. https://doi.org/10.3390/s23031625
APA StyleNeri, L., Oberdier, M. T., Augello, A., Suzuki, M., Tumarkin, E., Jaipalli, S., Geminiani, G. A., Halperin, H. R., & Borghi, C. (2023). Algorithm for Mobile Platform-Based Real-Time QRS Detection. Sensors, 23(3), 1625. https://doi.org/10.3390/s23031625