Deep Ordinal Classification in Forest Areas Using Light Detection and Ranging Point Clouds
Abstract
:1. Introduction
- The development of an ordinal classification model that utilizes an effective soft labeling technique applied to the loss function using unimodal distributions to ameliorate the classification of LiDAR data.
- The application of the proposed methodology in forest areas where LiDAR point clouds can be classified into four distinct ordinal labels: ground, low vegetation, medium vegetation, and high vegetation. In the field of Forestry Engineering, it is the first time that this kind of problem is treated as an ordinal regression problem. This contribution is particularly relevant for the forestry industry as it enables more accurate estimation of important forest metrics such as biomass and wood estimates.
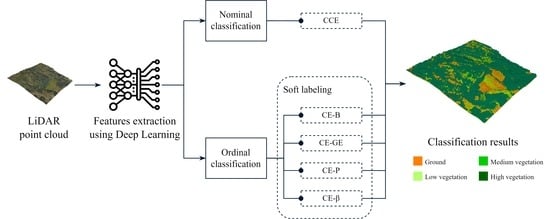
2. Materials and Methods
2.1. LiDAR Data
2.2. Ordinal Classification
2.3. Soft Labeling
2.4. Generalized Exponential Function
2.5. PointNet Network Architecture
2.6. Experiment Settings
3. Results
3.1. Calculating p and from Generalized Exponential Function
3.2. Statistical Analysis
3.3. LiDAR Classification
4. Discussion
5. Conclusions
- Significant differences in the paired t-test were observed, in which the CE-GE method reached the best mean results for all the metrics (QWK, MS, MAE, CCR, and 1-off) when compared to the other methods.
- Regarding the confusion matrices of the best alternative conceived (CE-GE + Softmax) and the standard method (CCE + Softmax), the smoothed ordinal classification achieved notably better results than the nominal one. Consequently, our methodology reduce the errors in distinguishing between the middle classes (low vegetation and medium vegetation).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Hyperparameter from the Generalized Exponential Function
| p | QWK 1 | MS 1 | MAE 1 | CCR 1 | 1-off 1 | mIoU 1 |
|---|---|---|---|---|---|---|
| 1.0 | ||||||
| 1.1 | ||||||
| 1.2 | ||||||
| 1.3 | ||||||
| 1.4 | ||||||
| 1.5 | ||||||
| 1.6 | ||||||
| 1.7 | ||||||
| 1.8 | ||||||
| 1.9 | ||||||
| 2.0 |
| QWK 1 | MS 1 | MAE 1 | CCR 1 | 1-off 1 | mIoU 1 | |
|---|---|---|---|---|---|---|
| 0.25 | ||||||
| 0.50 | ||||||
| 0.75 | ||||||
| 1.00 | ||||||
| 1.25 | ||||||
| 1.50 | ||||||
| 1.75 | ||||||
| 2.00 |
References
- Li, L.; Mu, X.; Chianucci, F.; Qi, J.; Jiang, J.; Zhou, J.; Chen, L.; Huang, H.; Yan, G.; Liu, S. Ultrahigh-resolution Boreal Forest Canopy Mapping: Combining UAV Imagery and Photogrammetric Point Clouds in a Deep-learning-based Approach. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102686. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, Z.; Li, W.; Chen, Y.; Wang, C.; Nurunnabi, A.A.M.; Li, J. Detection of Individual Trees in UAV LiDAR Point Clouds Using a Deep Learning Framework Based on Multichannel Representation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Gao, S.; Wu, F.; Ma, Q.; Xu, K.; Ma, Q.; Hu, T.; Liu, J.; Pang, S.; et al. Separating the Structural Components of Maize for Field Phenotyping Using Terrestrial LiDAR Data and Deep Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2644–2658. [Google Scholar] [CrossRef]
- Zhou, C.; Ye, H.; Sun, D.; Yue, J.; Yang, G.; Hu, J. An automated, high-performance approach for detecting and characterizing broccoli based on UAV remote-sensing and transformers: A case study from Haining, China. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103055. [Google Scholar] [CrossRef]
- Fang, L.; Sun, T.; Wang, S.; Fan, H.; Li, J. A graph attention network for road marking classification from mobile LiDAR point clouds. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102735. [Google Scholar] [CrossRef]
- Kalinicheva, E.; Landrieu, L.; Mallet, C.; Chehata, N. Predicting Vegetation Stratum Occupancy from Airborne LiDAR Data with Deep Learning. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102863. [Google Scholar] [CrossRef]
- Moudrý, V.; Klápště, P.; Fogl, M.; Gdulová, K.; Barták, V.; Urban, R. Assessment of LiDAR Ground Filtering Algorithms for Determining Ground Surface of Non-natural Terrain Overgrown with Forest and Steppe Vegetation. Measurement 2020, 150, 107047. [Google Scholar] [CrossRef]
- ASPRS. LAS Specification Version 1.4-R13; The American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2013. [Google Scholar]
- Vosselman, G.; Maas, H.G. Adjustment and Filtering of Raw Laser Altimetry Data. In Proceedings of the OEEPE workshop on Airborne Laserscanning and Interferometric SAR for Detailed Digital Elevation Models, Stockhom, Sweden, 1–3 March 2001. [Google Scholar]
- Sithole, G.; Vosselman, G. Experimental Comparison of Filter Algorithms for Bare-Earth Extraction from Airborne Laser Scanning Point Clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Yunfei, B.; Guoping, L.; Chunxiang, C.; Xiaowen, L.; Hao, Z.; Qisheng, H.; Linyan, B.; Chaoyi, C. Classification of LIDAR Point Cloud and Generation of DTM from LIDAR Height and Intensity Data in Forested Area. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 313–318. [Google Scholar]
- Shan, J.; Aparajithan, S. Urban DEM Generation from Raw LiDAR Data Vegetation. Photogramm. Eng. Remote Sens. 2005, 71, 217–226. [Google Scholar] [CrossRef]
- Samadzadegan, F.; Hahn, M.; Bigdeli, B. Automatic Road Extraction from LiDAR Data Based on Classifier Fusion. In Proceedings of the Joint Urban Remote Sensing Event, Shanghai, China, 20–22 May 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Andersen, H.E.; McGaughey, R.J.; Reutebuch, S.E. Estimating Forest Canopy Fuel Parameters Using LiDAR Data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest Biomass Estimation from Airborne LiDAR Data Using Machine Learning Approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The Use of Terrestrial LiDAR Technology in Forest Science: Application Fields, Benefits and Challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- González-Olabarria, J.; Rodríguez, F.; Fernández-Landa, A.; Mola-Yudego, B. Mapping Fire Risk in the Model Forest of Urbión Based on Airborne LiDAR Measurements. For. Ecol. Manag. 2012, 282, 149–256. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Zhang, L.; Li, R.; Zheng, Y.; Zhu, Z. A Deep Neural Network With Spatial Pooling (DNNSP) for 3-D Point Cloud Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4594–4604. [Google Scholar] [CrossRef]
- Zhao, P.; Guan, H.; Li, D.; Yu, Y.; Wang, H.; Gao, K.; Marcato Junior, J.; Li, J. Airborne Multispectral LiDAR Point Cloud Classification with a Feature Reasoning-based Graph Convolution Network. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102634. [Google Scholar] [CrossRef]
- Shichao, J.; Yanjun, S.; Shang, G.; Fangfang, W.; Tianyu, H.; Jin, L.; Wenkai, L.; Wang, D.; Chen, S.; Jiang, Y.; et al. Deep Learning: Individual Maize Segmentation From Terrestrial Lidar Data Using Faster R-CNN and Regional Growth Algorithms. Front. Plant Sci. 2018, 9, 866. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, L.; Waslander, S.L.; Liu, X. An end-to-end shape modeling framework for vectorized building outline generation from aerial images. ISPRS J. Photogramm. Remote Sens. 2020, 170, 114–126. [Google Scholar] [CrossRef]
- Ramiya, A.; Nidamanuri, R.R.; Krishnan, R. Semantic labelling of urban point cloud data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-8, 907–911. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, Y. Deep-Learning-Based Classification for DTM Extraction from ALS Point Cloud. Remote Sens. 2016, 8, 730. [Google Scholar] [CrossRef]
- Huang, J.; You, S. Point Cloud Labeling Using 3D Convolutional Neural Network. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2670–2675. [Google Scholar] [CrossRef]
- Kowalczuk, Z.; Szymański, K. Classification of objects in the LIDAR point clouds using Deep Neural Networks based on the PointNet model. IFAC-PapersOnLine 2019, 52, 416–421. [Google Scholar] [CrossRef]
- Eroshenkova, D.A.; Terekhov, V.I.; Khusnetdinov, D.R.; Chumachenko, S.I. Automated Determination of Forest-Vegetation Characteristics with the Use of a Neural Network of Deep Learning. In Advances in Neural Computation, Machine Learning, and Cognitive Research III; Kryzhanovsky, B., Dunin-Barkowski, W., Redko, V., Tiumentsev, Y., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 295–302. [Google Scholar] [CrossRef]
- Qi, C.; Su, H.; Mo, K.; Guibas, L. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Jing, Z.; Guan, H.; Zhao, P.; Li, D.; Yu, Y.; Zang, Y.; Wang, H.; Li, J. Multispectral LiDAR Point Cloud Classification Using SE-PointNet++. Remote Sens. 2021, 13, 2516. [Google Scholar] [CrossRef]
- Jayakumari, R.; Nidamanuri, R.; Ramiya, A. Object-level Classification of Vegetable Crops in 3D LiDAR Point Cloud using Deep Learning Convolutional Neural Networks. Precis. Agric. 2021, 22, 1617–1633. [Google Scholar] [CrossRef]
- Soilán, M.; Lindenbergh, R.; Riveiro, B.; Sánchez-Rodríguez, A. PointNet for the Automatic Classification of Aerial Point Clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, IV-2/W5, 445–452. [Google Scholar] [CrossRef]
- Soilán, M.; Riveiro, B.; Balado, J.; Arias, P. Comparison of Heuristic and Deep Learning-Based Methods for Ground Classification from Aerial Point Clouds. Int. J. Digit. Earth 2020, 13, 1.115–1.134. [Google Scholar] [CrossRef]
- Hsu, P.H.; Zhuang, Z.Y. Incorporating Handcrafted Features into Deep Learning for Point Cloud Classification. Remote Sens. 2020, 12, 3713. [Google Scholar] [CrossRef]
- Gamal, A.; Husodo, A.Y.; Jati, G.; Alhamidi, M.R.; Ma’sum, M.A.; Ardhianto, R.; Jatmiko, W. Outdoor LiDAR Point Cloud Building Segmentation: Progress and Challenge. In Proceedings of the International Conference on Advanced Computer Science and Information Systems (ICACSIS), Depok, Indonesia, 23–25 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Teferle, F.; Li, J.; Lindenbergh, R.; Parvaz, S. Investigation of Pointnet for Semantic Segmentation of Large-Scale Outdoor Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 46, 397–404. [Google Scholar] [CrossRef]
- Briechle, S.; Krzystek, P.; Vosselman, G. Silvi-Net – A Dual-CNN Approach for Combined Classification of Tree Species and Standing Dead Trees from Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102292. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, K.; Zhu, Y.; Wang, X.; Yun, T. Individual Tree Crown Segmentation Directly from UAV-Borne LiDAR Data Using the PointNet of Deep Learning. Forests 2021, 12, 131. [Google Scholar] [CrossRef]
- Winiwarter, L.; Mandlburger, G.; Schmohl, S.; Pfeifer, N. Classification of ALS point clouds using end-to-end deep learning. PFG- Photogramm. Remote Sens. Geoinf. Sci. 2019, 87, 75–90. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, R.; Yang, C.; Lin, Y. Urban vegetation segmentation using terrestrial LiDAR point clouds based on point non-local means network. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102580. [Google Scholar] [CrossRef]
- Xiao, S.; Sang, N.; Wang, X.; Ma, X. Leveraging Ordinal Regression with Soft Labels For 3d Head Pose Estimation From Point Sets. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1883–1887. [Google Scholar] [CrossRef]
- Arvidsson, S.; Gullstrand, M. Predicting Forest Strata from Point Clouds Using Geometric Deep Learning. Master’s Thesis, Department of Computing, JTH, Jönköping, Sweden, 2021. [Google Scholar]
- HERE Europe, B.V. PPTK 0.1.1 Documentation Point Processing Toolkit. 2018. Available online: https://heremaps.github.io/pptk/index.html (accessed on 15 February 2024).
- Netherlands eScience Center. Laserchicken 0.4.2 Documentation. 2019. Available online: https://laserchicken.readthedocs.io/en/latest/ (accessed on 15 February 2024).
- Girardeau-Montaut, D. CloudCompare: 3D Point Cloud and Mesh Processing Software. Version 2.12.0. 2021. Available online: https://www.danielgm.net/cc/ (accessed on 15 February 2024).
- Manduchi, G. Commonalities and Differences Between MDSplus and HDF5 Data Systems. Fusion Eng. Des. 2010, 85, 583–590. [Google Scholar] [CrossRef]
- Cruz-Ramírez, M.; Hervás-Martínez, C.; Sánchez-Monedero, J.; Gutiérrez, P. Metrics to Guide a Multi-objective Evolutionary Algorithm for Ordinal Classification. Neurocomputing 2014, 135, 21–31. [Google Scholar] [CrossRef]
- Zhang, C.B.; Jiang, P.T.; Hou, Q.; Wei, Y.; Han, Q.; Li, Z.; Cheng, M.M. Delving Deep Into Label Smoothing. IEEE Trans. Image Process. 2021, 30, 5984–5996. [Google Scholar] [CrossRef] [PubMed]
- Vargas, V.; Gutiérrez, P.; Hervás-Martínez, C. Unimodal Regularisation based on Beta Distribution for Deep Ordinal Regression. Pattern Recognit. 2022, 122, 108310. [Google Scholar] [CrossRef]
- Li, L.; Doroslovački, M.; Loew, M.H. Approximating the Gradient of Cross-Entropy Loss Function. IEEE Access 2020, 8, 111626–111635. [Google Scholar] [CrossRef]
- Pinto da Costa, J.F.; Alonso, H.; Cardoso, J.S. The Unimodal Model for the Classification of Ordinal Data. Neural Netw. 2008, 21, 78–91. [Google Scholar] [CrossRef]
- Beckham, C.; Pal, C. Unimodal Probability Distributions for Deep Ordinal Classification. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 411–419. [Google Scholar]
- Liu, X.; Fan, F.; Kong, L.; Diao, Z.; Xie, W.; Lu, J.; You, J. Unimodal Regularized Neuron Stick-Breaking for Ordinal Classification. Neurocomputing 2020, 388, 34–44. [Google Scholar] [CrossRef]
- Bérchez-Moreno, F.; Barbero, J.; Vargas, V.M. Deep Learning Utilities Library. 2023. Available online: https://dlordinal.readthedocs.io/en/latest/index.html (accessed on 15 February 2024).
- Yousefhussien, M.; Kelbe, D.J.; Ientilucci, E.J.; Salvaggio, C. A Multi-Scale Fully Convolutional Network for Semantic Labeling of 3D Point Clouds. ISPRS J. Photogramm. Remote Sens. 2018, 143, 191–204. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Dodge, Y. The Concise Encyclopedia of Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Zhang, L.; Zhang, L. Deep Learning-Based Classification and Reconstruction of Residential Scenes From Large-Scale Point Clouds. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1887–1897. [Google Scholar] [CrossRef]
- Zhou, Y.; Ji, A.; Zhang, L.; Xue, X. Sampling-attention deep learning network with transfer learning for large-scale urban point cloud semantic segmentation. Eng. Appl. Artif. Int. 2023, 117, 105554. [Google Scholar] [CrossRef]







| Category | Training | Validation | Test |
|---|---|---|---|
| Ground | 2,578,600 | 863,096 | 835,056 |
| Low vegetation | 1,000,907 | 324,547 | 354,049 |
| Medium vegetation | 1,204,729 | 412,513 | 400,521 |
| High vegetation | 2,264,980 | 750,948 | 761,478 |
| 7,049,216 | 2,351,104 | 2,351,104 |
| Predicted Class | |||||||
|---|---|---|---|---|---|---|---|
| 1 | ⋯ | ⋯ | |||||
| 1 | ⋯ | ⋯ | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ||||
| True class | q | ⋯ | ⋯ | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ||||
| Q | ⋯ | ⋯ | |||||
| ⋯ | ⋯ | n | |||||
| Method 1 | QWK | MS | MAE | CCR | 1-off | mIoU |
|---|---|---|---|---|---|---|
| CCE | 0.95350.0258 | 0.80770.1281 | 0.09200.0495 | 0.93780.0310 | 0.97030.0187 | 0.87570.0393 |
| CE-B | ||||||
| CE-P | ||||||
| CE- | ||||||
| CE-GE |
| Metric | Paired Sample 1 | Mean | SD | p-Value |
|---|---|---|---|---|
| QWK | CE-GE vs CCE | 0.014 | 0.026 | 0.024 |
| CE-GE vs. CE- | 0.017 | 0.041 | 0.081 | |
| CE-GE vs. CE-B | 0.021 | 0.027 | 0.003 | |
| CE-GE vs. CE-P | 0.028 | 0.052 | 0.023 | |
| MS | CE-GE vs CCE | 0.044 | 0.142 | 0.182 |
| CE-GE vs. CE- | 0.077 | 0.172 | 0.061 | |
| CE-GE vs. CE-B | 0.083 | 0.130 | 0.010 | |
| CE-GE vs. CE-P | 0.106 | 0.216 | 0.040 | |
| MAE | CE-GE vs CCE | −0.025 | 0.050 | 0.034 |
| CE-GE vs. CE- | −0.033 | 0.071 | 0.050 | |
| CE-GE vs. CE-B | −0.043 | 0.055 | 0.002 | |
| CE-GE vs. CE-P | −0.053 | 0.094 | 0.021 | |
| CCR | CE-GE vs CCE | 0.016 | 0.030 | 0.024 |
| CE-GE vs. CE- | 0.022 | 0.046 | 0.044 | |
| CE-GE vs. CE-B | 0.030 | 0.039 | 0.003 | |
| CE-GE vs. CE-P | 0.033 | 0.056 | 0.017 | |
| 1-off | CE-GE vs CCE | 0.010 | 0.019 | 0.033 |
| CE-GE vs. CE- | 0.012 | 0.030 | 0.089 | |
| CE-GE vs. CE-B | 0.014 | 0.018 | 0.003 | |
| CE-GE vs. CE-P | 0.019 | 0.038 | 0.035 | |
| mIoU | CE-GE vs CCE | 0.013 | 0.049 | 0.174 |
| CE-GE vs. CE- | 0.030 | 0.083 | 0.082 | |
| CE-GE vs. CE-B | 0.047 | 0.082 | 0.012 | |
| CE-GE vs. CE-P | 0.050 | 0.111 | 0.022 |
| Ground | Low Vegetation | Medium Vegetation | High Vegetation | |
|---|---|---|---|---|
| Ground | 827,294 | 7667 | 95 | 0 |
| Low vegetation | 12,368 | 341,629 | 52 | 0 |
| Medium vegetation | 23,385 | 4259 | 372,858 | 19 |
| High vegetation | 0 | 0 | 8083 | 753,395 |
| Ground | Low Vegetation | Medium Vegetation | High Vegetation | |
|---|---|---|---|---|
| Ground | 815,576 | 17,125 | 2355 | 0 |
| Low vegetation | 3973 | 350,035 | 41 | 0 |
| Medium vegetation | 12,363 | 7723 | 378,657 | 1778 |
| High vegetation | 0 | 0 | 1258 | 760,220 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales-Martín, A.; Mesas-Carrascosa, F.-J.; Gutiérrez, P.A.; Pérez-Porras, F.-J.; Vargas, V.M.; Hervás-Martínez, C. Deep Ordinal Classification in Forest Areas Using Light Detection and Ranging Point Clouds. Sensors 2024, 24, 2168. https://doi.org/10.3390/s24072168
Morales-Martín A, Mesas-Carrascosa F-J, Gutiérrez PA, Pérez-Porras F-J, Vargas VM, Hervás-Martínez C. Deep Ordinal Classification in Forest Areas Using Light Detection and Ranging Point Clouds. Sensors. 2024; 24(7):2168. https://doi.org/10.3390/s24072168
Chicago/Turabian StyleMorales-Martín, Alejandro, Francisco-Javier Mesas-Carrascosa, Pedro Antonio Gutiérrez, Fernando-Juan Pérez-Porras, Víctor Manuel Vargas, and César Hervás-Martínez. 2024. "Deep Ordinal Classification in Forest Areas Using Light Detection and Ranging Point Clouds" Sensors 24, no. 7: 2168. https://doi.org/10.3390/s24072168
APA StyleMorales-Martín, A., Mesas-Carrascosa, F. -J., Gutiérrez, P. A., Pérez-Porras, F. -J., Vargas, V. M., & Hervás-Martínez, C. (2024). Deep Ordinal Classification in Forest Areas Using Light Detection and Ranging Point Clouds. Sensors, 24(7), 2168. https://doi.org/10.3390/s24072168