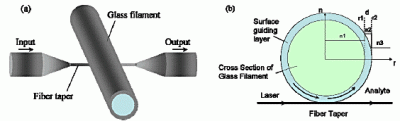
Modeling of an Optical Sensor Based on Whispering Gallery Modes (WGMs) on the Surface Guiding Layer of Glass Filaments
Abstract
:1. Introduction
2. Theory and Simulations
3. Conclusions
Acknowledgments
References and Notes
- Chao, C.Y.; Guo, L.J. Biochemical sensors based on polymer microrings with sharp asymmetrical resonance. Appl. Phys. Lett. 2003, 83, 1527–1529. [Google Scholar]
- Yalçin, A.; Popat, K.C.; Aldridge, J.C.; Desai, T.A.; Hryniewicz, J.; Chbouki, N.; Little, B.E.; King, O.; Van, V.; Vhu, S.; Gill, D.; Anthes-Washburn, M.; Ünlü, M.S.; Goldberg, B.B. Optical sensing of biomolecules using microring resonators. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 148–155. [Google Scholar]
- Guo, X.; Tong, L. Supported microfiber loops for optical sensing. Opt. Express 2008, 16, 14429–14434. [Google Scholar]
- Cho, S.Y.; Jokerst, N.M. A polymer microdisk photonic sensor integrated onto silicon. IEEE Photon. Technol. Lett. 2006, 18, 2096–2098. [Google Scholar]
- Arnold, S.; Khoshsima, M.; Teraoka, I.; Holler, S.; Vollmer, F. Shift of whispering-gallery modes in microspheres by protein adsorption. Opt. Lett. 2003, 28, 272–274. [Google Scholar]
- Hanumegowda, N.M.; Stica, C.J.; Patel, B.C.; White, I.M.; Fan, X. Refractometric sensors based on microsphere resonators. Appl. Phys. Lett. 2005, 87, 201107. [Google Scholar]
- White, I.M.; Oveys, H.; Fan, X. Liquid-core optical ring-resonator sensors. Opt. Lett. 2006, 31, 1319–1321. [Google Scholar]
- White, I.M.; Oveys, H.; Fan, X.; Smith, T.L.; Zhang, J. Integrated multiplexed biosensors based on liquid core optical ring resonators and antiresonant reflecting optical waveguides. Appl. Phys. Lett. 2006, 89, 191106. [Google Scholar]
- White, I.M.; Zhu, H.; Suter, J.D.; Hanumegowda, N.M.; Oveys, H.; Zourob, M.; Fan, X. Refractometric sensors for Lab-on-a-chip based on optical ring resonators. IEEE Sens. J. 2007, 7, 28–35. [Google Scholar]
- Zamora, V.; Díez, A.; Andrés, M.V.; Gimeno, B. Refractometric sensor based on whispering-gallery modes of thin capillarie. Opt. Express 2007, 15, 12011–12016. [Google Scholar]
- Ling, T.; Guo, L.J. A unique resonance mode observed in a prism-coupled micro-tube resonator sensor with superior index sensitivity. Opt. Express 2007, 15, 17424–17432. [Google Scholar]
- Zou, J.; Zhao, F.; Chen, R.T. Two-step K+-Na+ and Ag+-Na+ ion-exchanged glass waveguides for C-band applications. Appl. Opt. 2002, 41, 7620–7626. [Google Scholar]
- Gaathon, O.; Culic-Viskota, J.; Mihnev, M.; Teraoka, I.; Arnold, S. Enhancing sensitivity of a whispering gallery mode biosensor by subwavelength confinement. Appl. Phys. Lett. 2006, 89, 223901. [Google Scholar]
- Teraoka, I.; Arnold, S. Enhancing the sensitivity of a whispering-gallery mode microsphere sensor by a high-refractive-index surface layer. J. Opt. Soc. Am. B 2006, 23, 1434–1441. [Google Scholar]
- Tong, L.; Hu, L.; Zhang, J.; Qiu, J.; Yang, Q.; Lou, J.; Shen, Y.; He, J.; Ye, Z. Photonic nanowires directly drawn from bulk glasses. Opt. Express 2006, 14, 82–87. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and scattering of light by small particles; Wiley: New York, USA, 1998. [Google Scholar]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-Insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar]
- Rowland, D.R.; Love, J.D. Evanescent wave coupling of whispering gallery modes of a dielectric cylinder. Optoelectronics[see also IEE Proceedings-Optoelectronics], IEE Proceedings J 1993, 140, 177–188. [Google Scholar]
- Knight, J.C.; Cheung, G.; Jacques, F.; Birks, T.A. Phase-matched excitation of whispering-gallery-mode resonances by a fiber taper. Opt. Lett. 1997, 22, 1129–1131. [Google Scholar]
- Cai, M.; Painter, O.; Vahala, K.J. Observation of Critical Coupling in a Fiber Taper to a Silica-Microsphere Whispering-Gallery Mode System. Phys. Rev. Lett. 2000, 85, 74. [Google Scholar]
- Subramaniam, V.; De Brabander, G.N.; Naghski, D.H.; Boyd, J.T. Measured of mode field profiles and bending and transition losses in curved optical channel waveguides. J. Lightwave Technol. 1997, 15, 990–997. [Google Scholar]
- Gorodetsky, M.L.; Savchenkov, A.A.; Ilchenko, V.S. Ultimate Q of optical microsphere resonators. Opt. Lett. 1996, 21, 453–455. [Google Scholar]
- White, I.M.; Suter, J.D.; Oveys, H.; Fan, X.D. Universal coupling between metal-cald waveguide and optical ring resonators. Opt. Express 2007, 15, 646–651. [Google Scholar]
- Chao, C.Y.; Fung, W.; Guo, L.J. Polymer microring resonators for biochemical sensing application. IEEE J. Selected Top. Quantum Electron. 2006, 12, 134–142. [Google Scholar]






© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tan, W.; Shi, L.; Chen, X. Modeling of an Optical Sensor Based on Whispering Gallery Modes (WGMs) on the Surface Guiding Layer of Glass Filaments. Sensors 2008, 8, 6761-6768. https://doi.org/10.3390/s8106761
Tan W, Shi L, Chen X. Modeling of an Optical Sensor Based on Whispering Gallery Modes (WGMs) on the Surface Guiding Layer of Glass Filaments. Sensors. 2008; 8(10):6761-6768. https://doi.org/10.3390/s8106761
Chicago/Turabian StyleTan, Wei, Lei Shi, and Xianfeng Chen. 2008. "Modeling of an Optical Sensor Based on Whispering Gallery Modes (WGMs) on the Surface Guiding Layer of Glass Filaments" Sensors 8, no. 10: 6761-6768. https://doi.org/10.3390/s8106761
APA StyleTan, W., Shi, L., & Chen, X. (2008). Modeling of an Optical Sensor Based on Whispering Gallery Modes (WGMs) on the Surface Guiding Layer of Glass Filaments. Sensors, 8(10), 6761-6768. https://doi.org/10.3390/s8106761